基于非侵入式负荷监测数据的居民相似邻里查找模型

葛 翔,山宪武,宋秩行,陈 术,高弘毅,孙永辉

(1.国网新疆电力有限公司营销服务中心,新疆 乌鲁木齐 830000;2.国网重庆市电力公司营销服务中心,重庆 401123: 3.河海大学 能源与电气学院,江苏 南京 211100)

近年来,中国各地长期电力供不应求,家庭用电占社会用电的比重日趋增大。在此背景下,增强居民节约用电意识显得尤为重要[1]。非侵入式负荷监测技术能够基于区域入的总电量的分解,实现区域内分项负荷的状态感知,如获取负荷的数量、种类、启停时间、工作状态以及对应的功率水平等[2-3]。由于具有成本低、普适性强等优点,基于智能电表的非侵入式负荷监测(Non-intrusive load monitoring,NILM)技术已经在世界各地得到广泛应用,为精细描述用户用电特征创造了条件[4]。计及用户负荷信息,基于用户用电行为特征分析,研究居民用户分类方法,已经成为重要的研究方向。

当前对于居民用户特征识别与分类的相关研究已取得了一些成果。文献[5]考虑将图结构用于表示社交网络,基于子图划分原理,实现复杂度较低,准确率较高的社交网络聚类。文献[6]运用K-means算法,根据负荷曲线的整体分布、局部动态与整体动态三种特性,自适应地获取权重系数,对日负荷曲线聚类。文献[7]根据地理位置、住宅面积、电器装置等特征建立了家庭特征匹配评分准则,通过得分排名寻找相似邻里。文献[8]首先根据海量电力数据从多角度建立用户特征标签体系,然后,基于改进K-means聚类算法对用户进行分类,将用户综合画像可视化呈现。文献[9]基于用电特征优选策略,设计了一种基于极限学习机的居民用户分类方法,算例测试证明了所提出方法的有效性。文献[10]利用基于密度的带噪声数据应用的空间聚类方法(Density based spatial clustering of applications with noise,DBSCAN)剔除异常数据,获取用户典型用电模式,再用引力搜索算法对用电模式进行聚类。上述研究在用户用电模式分类方面更多关注总负荷曲线,而较少考虑居民用户分项负荷曲线,难以精确本区分用户用电模式的差异化特征。

本文设计一种相似邻里查找模型,利用DBSCAN处理NILM数据,提取待查用户池中用户的分项负荷标准曲线,计算各分项负荷时间分布的余弦相似度,结合熵权法对各项余弦相似度进行加权,根据相似度排序结果查找相似邻里。最后以公开的居民用户用电数据集进行仿真分析,验证所述方法的有效性。

1 基于DBSCAN聚类的负荷预处理方法

1.1 问题描述

基于NILM技术采集的居民用户分项负荷曲线由采样点功率值表示为

(1)

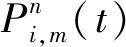
受多种因素(如高/低温、外出旅游等)的影响,居民用户在个别日的负荷曲线与一般负荷曲线存在较大差别,将这些负荷曲线称为异常负荷曲线。传统的曲线聚类手段对异常负荷曲线敏感,因此存在缺陷。

1.2 DBSCAN密度聚类算法

针对上述问题,同时考虑到居民用户的正常负荷曲线趋向于聚集在标准曲线附近,而异常曲线有时会偏离标准曲线,采用基于密度空间的聚类算法DBSCAN,提取一个月内居民用户分项负荷标准曲线。

DBSCAN算法能够将空间中分布密度大的点聚类为一簇,避免异常数据点对整体分析的干扰[11]。DBSCAN聚类算法的超参数为聚类半径ε和核心点阈值NMinPts。

为了有效地排除异常曲线,提取标准曲线,合理地设置核心参数ε及NMinPts,在多次测试的基础上,同时参考文献[12]提出的经验公式,采用如下设置DBSCAN算法参数的方法。

异常曲线占分项负荷曲线总数N的比重一般不超过20%,为了防止异常曲线的误划分,取

NMinPts=[N×20%]

(2)

考虑居民用户正常用电情况下,分项负荷曲线变化范围不超过最大分项负荷值10%,取聚类半径为

(3)

式中:T是每日采样点总数;Pmax为30日内最大负荷。

DBSCAN算法流程如图1所示。

图1 DBSCAN算法流程图

经过负荷预处理后,获取用户i的分项负荷标准曲线集

(4)

2 相似邻里查找流程

2.1 单一用户用电特征提取

为了避免数据不完整的用户和空置房对查找产生不利的影响,针对某一特定地区的居民用户,建立待查用户池。步骤包括:获取同一地区内所有过去30日分项NILM数据完整的用户数据;剔除异常用户,其中异常用户指过去12个月总用电量小于或等于200 kW·h,或者过去30天用电量小于或等于20 kW·h的用户。

在此基础上,采用上文所述的密度聚类算法,提取待查用户池中各用户的分项负荷标准曲线,作为相似邻里查找的依据。

2.2 余弦相似度

相似度函数是用于量化数据对象之间近似水平的一种测度,余弦相似度函数越趋向于1时双方近似水平越高。定义用户i和用户j关于负荷m的余弦相似度函数

(5)

式中:特别地,当某一向量为零向量,另一向量非零向量时,余弦相似度为零;当双方均未零向量时,余弦相似度为一。

为了描述两组离散数据在分布形态上的近似水平,序列向量的方向比模更值得关注,余弦相似度函数能够简单清晰地度量两个向量在角度上的相似度,适合用于基于分项负荷时间分布的相似邻里查找。

2.3 基于改进熵权法的加权排序

计算分项负荷的相似度后,将其加权求和,得到总相似度,以此为依据排序。熵权法的原理是用信息熵量化度量一组数据的变动水平的大小,其变动水平越大,数字越有价值,其比重也越大。传统熵权法具有权重对于接近于1的熵值过于敏感等缺点,因此采用改进熵权法求得各分项负荷相似度的权重[13]。其步骤如下:

(1)数据归一化,若要查找用户i的相似邻里,则用户j关于m负荷的归一化余弦相似度Rm(i,j)的计算方法为

(6)

式中:特别地,若max(Cm(i,j))和min(Cm(i,j))相等时,Rm(i,j)等于1。

(2)计算信息熵,关于负荷m的信息熵记为Em(i),表达式如下

(7)

(8)

式中:N为待查用户池用户总量。

(3)计算权重,负荷m的余弦相似度权重ωm(i)计算方式如下

(9)

(4)求总相似度,根据步骤(3)求得的权重,对分项负荷相似度加权,求得用户j对用户i的负荷时间分布总相似度S(i,j),由式(10)计算

(10)

(5)根据总相似度的排名情况,选取排名靠前的一定比例的居民用户作为相似邻里。文中取前7.5%用户作为相似邻里。

3 仿真分析

为了验证上述模型的有效性,选取UC Irvine School of Information and Computer Science公开的数据集作为分析实例。运用上述模型查找一名来自阿拉斯加安克雷奇的居民(记为用户1)的相似邻里。

3.1 分项负荷标准曲线提取实例分析

以居住于佛罗里达西棕榈滩的某用户为例,利用DBSCAN密度聚类算法对一月份的用电负荷进行预处理,提取标准曲线,结果如图2所示。该用户在一月份内大多数负荷曲线形态相似,但是存在2条曲线与其他曲线差异较大。通过DBSCAN密度聚类,将分布差异较大的2条标记为异常曲线,并将其余的曲线标记为正常曲线。图2示例证明,DBSCAN算法能够检测出异常用电行为,提取居民用户的标准负荷曲线。

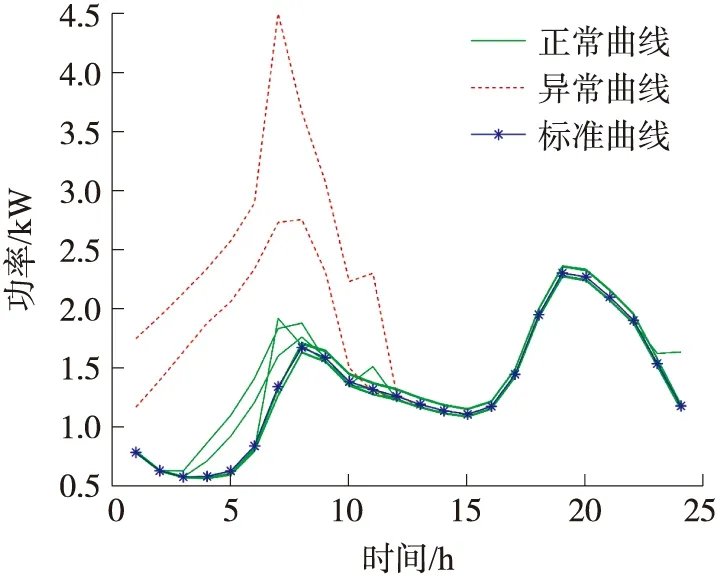
图2 分项负荷标准曲线提取实例

3.2 改进熵权法效果分析

以用户1为参考对象,先根据式(5)求其余用户与用户1的分项负荷标准曲线的余弦相似度,然后根据式(6)计算得到归一化余弦相似度,再根据式(7)和(8)计算各负荷的信息熵,各项负荷的余弦相似度的信息熵如表1所示。最后采用式(9)基于改进熵权法计算权重。传统熵权法采用式(11)计算得到权重。两种权重计算结果比较如图3所示。

(11)

图3 改进熵权法与传统熵权法比较

表1 各项负荷余弦相似度的信息熵

结合表1和图3看出,传统熵权法对于较小的熵值变化较为敏感,尤其对于处于0.95～1.00之间的熵值赋权时,微小的熵值差异也会引起权值的大幅波动。改进熵权法能够克服传统熵权法对于微小熵值差异过于敏感的缺点,具有平滑权重值的效果。

3.3 相似邻里提取结果分析

根据加权后得到的总相似度排名,选取排名前7.5%的用户,标记为相似邻里。采用文中提出的方法提取用户1的相似邻里,其部分分项负荷标准曲线和排名靠后的非相似邻里用户的部分分项负荷标准曲线如图4所示。

图4 相似邻里与非相似邻里部分分项负荷标准曲线

分析图4,对于负荷1,相似邻里标准负荷曲线形态基本相同,用电高峰出现在20点,而部分非相似邻里用电高峰出现在8点;对于负荷2,相似邻里0点到5点用电量相比非相似邻里较少,而18点的用电高峰则较多;图中负荷3为电热取暖器,相似邻里均不使用此负荷(使用燃气取暖),而非相似邻里多数使用了此负荷。总体而言,相似邻里之间的分项负荷曲线分布形态差异较小,用户具有类似的用电特征;非相似邻里的分项负荷时间分布与相似邻里之间差异较大。以上分析证明本文提出的方法能够有效地将具有类似用电特征的居民用户分类为一组相似邻里。

4 结束语

本文构建了一种基于NILM数据的相似邻里查找模型。考虑异常用电行为的干扰,使用DBSCAN算法剔除异常数据,提取用户的分项负荷标准曲线。针对传统熵权法存在的问题,由改进熵权法对各项负荷余弦相似度加权,根据相似度排序结果查找相似邻里。最后通过仿真分析证明文中方法的有效性。基于本文提出的相似邻里查找方法,将居民用户各负荷能耗水平与相似邻里进行对比分析,进而辅助定位高能耗来源和促进居民用户用电行为改善,将是下一步研究的重点。