扁平微槽道热管蒸发冷凝极限模型

周 豪，孙志坚，庞逸晨，俞自涛，2

（1.浙江大学 能源工程学院 热工与动力系统研究所，浙江 杭州 310027；2.浙江大学 能源清洁利用国家重点实验室，浙江 杭州 310027）

0 引 言

强化传热同时减小热管理系统的尺寸和体积一直是学者们深入研究的内容[1]。 目前已经开发了很多新型微冷却技术，其中，微热管技术自从1984 年被Cotter[2]首次提出后，是目前行之有效的方法之一。 热管利用工质的蒸发和冷凝进行传热，由于一般情况下相变潜热远大于显热，因此不需要在热源和冷源之间存在较大的温差，即可使热管具有较好的传热性能[3]。 此外，在一定饱和压力下相变发生时饱和温度是恒定的，因此热管还具有较好的均温性能[4]；同时，热管借助相变的原理省去了单相冷却技术所需的高泵浦功率要求[5]，不需额外的外部能耗。

在目前已经开发的多种新型微冷却技术中，扁平微槽道热管由于其优异的传热性能、良好的均温性、简便的加工方法等优势在电子器件冷却[6，7]等领域得到广泛的应用。 但热管的传热性能容易受到各种运行参数[8]和结构参数[9-11]的影响。 不同的应用场景对应着不同的运行参数，有不同的散热需求，针对特定的运行参数应选取合适的结构参数，如充液率[12]，使热管发挥最大传热能力。 而通过实验优化热管结构参数不但成本高，而且十分耗费时间和精力，因此，通过建立理论模型探究热管的传热极限具有十分重要的意义。

目前学者们主要开发了两类方法计算热管的传热极限。 第一类方法是根据传热极限的产生机制，建立经验关联式，分别描述冷凝传热极限、粘滞极限、冷冻启动极限、连续流动极限、声速极限、携带极限、毛细极限和沸腾极限[13-16]。 这一类方法简便直接，容易操作，但是由于热管的种类和形式过于繁多，关联式仅能提供基本的定性预测功能，并不能针对不同种类的热管均给出相对准确的传热极限预测结果。

针对扁平微槽道热管的多项研究表明，毛细极限是其主要传热极限[17，18]，因此，学者们建立了基于热管流动模型的毛细极限计算模型[17，19]。 该方法主要基于质量守恒、动量守恒Young-Laplace方程，具有较高的精度且能从本质上描述热管发生传热极限的机理，因而具有较大的工程应用和理论指导价值。 但在这类方法中，学者们普遍仅考虑了由于蒸发段蒸干导致的毛细极限，而没有考虑随着充液率或加热功率的增加，冷凝段出现液堵所导致的毛细极限[20]，这是需要改进的地方。

本文提出了一种基于一维流动模型的铝—丙酮扁平微槽道热管毛细极限模型，同时考虑了由于蒸发段蒸干导致的蒸发极限和由于冷凝段液堵导致的冷凝极限，在液堵段考虑了接触角的变化。针对一维流动模型、蒸发极限模型和冷凝极限模型三部分分别给出求解算法，并以此探究充液率对热管性能的影响。 文中给出了流场参数、蒸发极限和冷凝极限随充液率变化的计算结果并进行相应讨论。

1 模型建立

1.1 一维流动模型建立

本文所研究的扁平微槽道热管单一槽道如图1（a）所示，槽道形状为梯形，槽道截面尺寸如图1（b）所示。 扁平微槽道热管的蒸发和冷凝极限模型是建立在流动模型的基础上，由于槽道的轴向尺寸比截面尺寸要大的多，同时考虑到热管的对称性，仅需要对一条槽道建立一维模型[21]。提出如下假设：（1）汽液两相均不可压缩；（2）工质的热物性不沿热管轴向变化；（3）流动为层流；（4）弯液面的轴向曲率半径为无穷大；（5）热管水平放置，忽略重力影响。

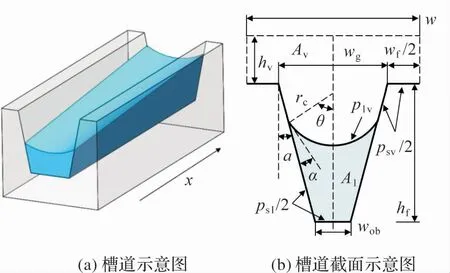
图1 槽道形状与截面尺寸

质量守恒关系如图2（a）所示，质量守恒方程为：

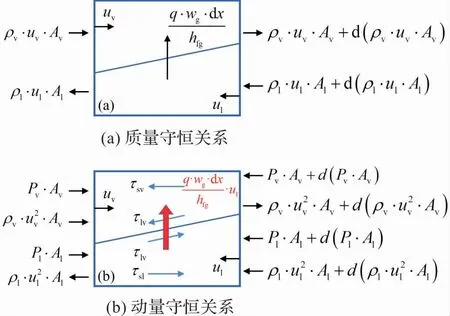
图2 质量与动量守恒关系

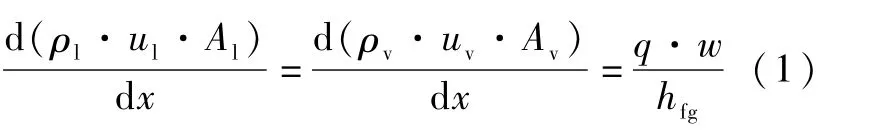
式中，下标l和v分别表示液相和气相，ρ为密度，u为速度，A为截面积，w为单个槽道的宽度，hfg为汽化潜热，x为轴向坐标，q为热流密度，由式（2）计算。

式中，下标e和c分别表示蒸发段和冷凝段，l为长度，Qin为蒸发段的加热功率，本文仅考虑蒸发段均匀加热的情况，且为了简便计算，假定冷凝段也为均匀热流边界条件，同时本文研究热管的稳态，假定冷凝段总换热功率等于蒸发段的加热功率Qin。

以蒸发段为例的动量守恒关系如图2（b）所示，绝热段和冷凝段同理，其中，控制体内由于相变导致的动量变化被考虑在内，液相和气相的动量守恒方程分别为

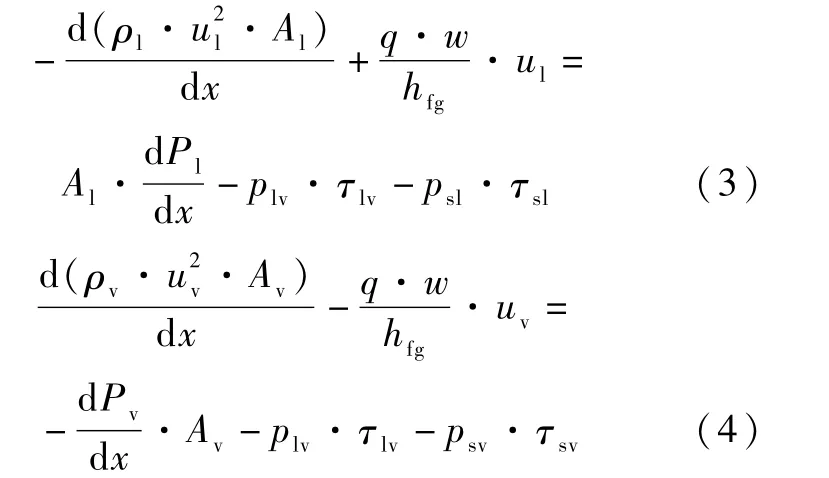
式中，下标s表示固相，P为压力，p为界面长度，τ为剪切应力。

在扁平微槽道热管中，有表面张力产生的毛细压力是驱动冷凝段液化工质回流的主要驱动力，毛细现象由Laplace-Young方程描述，如式（5）所示。

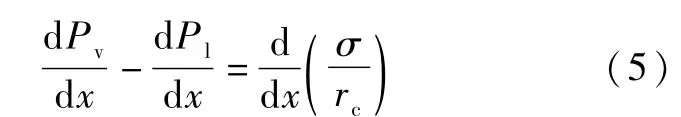
式中，σ为表面张力，rc为截面上弯月面半径。

由于已经假定流动为层流，所以对气液两相均有

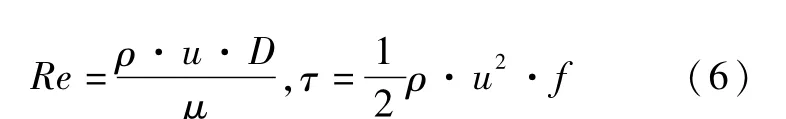
式中，Re为雷诺数，D为槽道当量直径计算方法如式（7）所示，μ为工质动力粘度，f为摩擦系数。摩擦系数f和雷诺数Re的乘积为泊肃叶数Po，泊肃叶数Po是仅取决于几何结构的无量纲数，在本文中，液相和气相的泊肃叶数Po分别取值14.2 和24[17]。 此外，由于气相速度和液相速度相差很大，气液界面处的剪切应力计算可以假设液相静止。

式中，θ为弯月面对应圆心角，δ为液膜厚度，其余几何参数于图1（b）中标出。

1.2 蒸发极限模型建立

蒸发极限模型已经被学者们广泛研究，本文仅做简要介绍。 随着加热功率的提高，蒸发段的工质不断蒸发并流向冷凝段，如果槽道表面提供的毛细力不足以将冷凝段液化的工质及时输运回蒸发段，就会产生蒸发段蒸干的现象，此时，热管的总热阻会迅速增加，蒸发段表面的温度会急速上升，达到蒸发极限。 判定热管达到毛细极限的标准为蒸发段初始处弯月面半径达到最小值，如式（14）所示，此时弯月面底部接触槽道底部。 此类情况在热管充液率较低时更容易发生，具体求解算法请参见本文2.2 节。

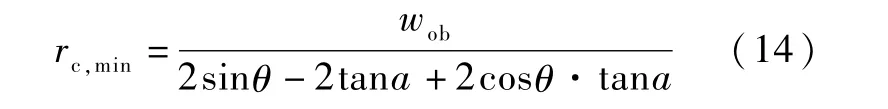
式中，a 为槽道倾斜角。

1.3 冷凝极限模型建立

除蒸发段蒸干可能导致扁平微槽道热管达到毛细极限之外，对于充液率较大的热管，冷凝段的液堵也是使热管达到毛细极限的条件之一，而这一问题往往被学者们忽略。

液堵段液膜分布如图3 所示。 在未出现液堵时，冷凝段末端的液膜位于1 位置，弯月面上沿尚未接触到槽道的顶角处。 随着加热功率的提升，冷凝段末端的液膜位置逐渐上移，首先达到2 位置，此时弯月面上沿刚好接触槽道的顶角处。 此前的多项研究均认为此时热管达到了毛细极限，其实并非如此。 由于表面张力的存在，随着加热功率继续增加，液膜后续并不会溢出槽道，而是会有一个液膜逐渐变平、接触角逐渐变大的过程，液膜形状会从形状2 逐渐向形状5 过渡，而液膜形状为2 的位置会从冷凝段末端向蒸发段的方向逐渐移动。 在本文中约定，液膜形状为2 的位置到冷凝段末端之间的部分为液堵段。

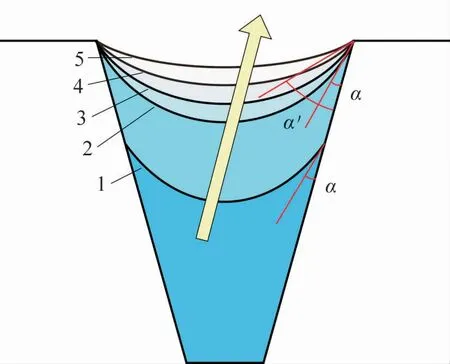
图3 液堵段液膜变化示意图

在液堵段，工质的接触角会沿热管轴向发生变化，接触角和弯月面半径之间的关系如式（15）所示。 在求解过程中，只需要把式（8） ～式（13）中的θ用θx进行替换，就可以照常计算，不会增加新的变量。

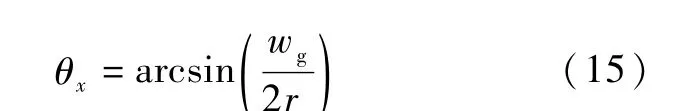
根据液堵段的定义，冷凝段末端的弯月面半径可以趋于无穷大，且液堵段的长度可以等于热管的总长度，这明显是不合理的，因此，本文假定，当液堵段的长度等于冷凝段的长度时，热管达到冷凝极限，此时冷凝段初始位置的弯月面顶部恰好上升至槽道顶部，此处弯月面半径值如式（16）所示。

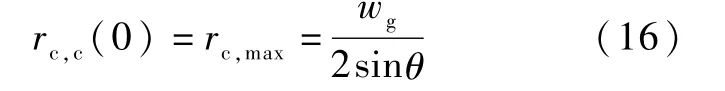
2 模型求解算法

2.1 一维流动模型求解

在一维流动模型中，式（1）、式（3） ～式（5）共同构成了二阶常微分方程组，共五个方程，含有ul、uv、Pl、Pv、rc五个变量，可以使用四阶龙格库塔方法进行求解，只需要指定迭代初值和迭代步长。 在本文中，迭代初值如式所示，迭代步长选取为0.001 m。

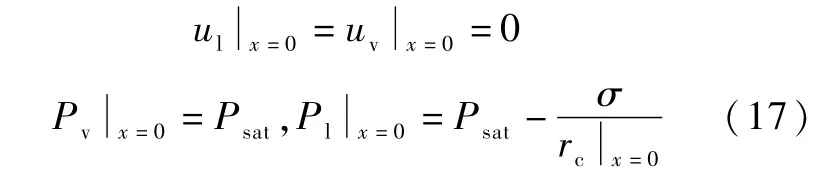
式中，Psat表示工作温度所对应的饱和压力，工作温度为事先设定值，此外，弯月面半径rc的初值选取与求解的过程有关，具体请参见本文2.2 节和2.3 节。

本文所研究热管工质为丙酮，管壳材质为铝，工质的物性参数根据工作温度值进行差值选取，物性数据库选用Nist数据库，差值方法为MATLAB R2019b 保型三段插值法。 本文所研究扁平微槽道热管的几何参数如表1 所示。 本文所有程序通过MATLAB R2019b 实现。

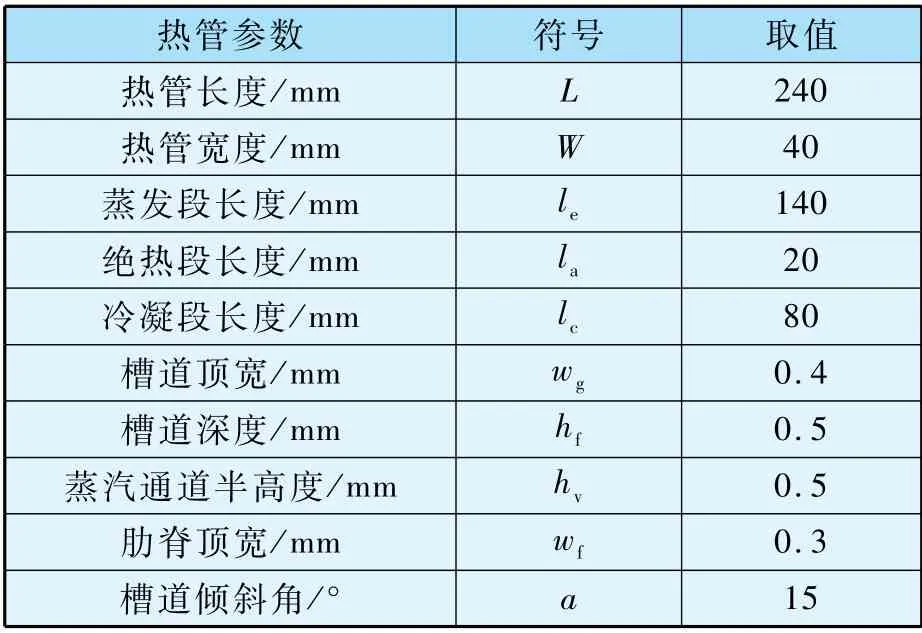
表1 扁平微槽道热管几何结构参数

2.2 蒸发极限模型求解

本小节提出了求解给定扁平微槽道热管蒸发极限计算的方法。 对于给定的扁平微槽道热管，充液率是确定，而充液率并不在模型的输入参数中，只能通过模型输出的液膜分布来核算，因此需要使用迭代求解的方法去逼近所给定的充液率值。

首先需要求解流动模型，迭代初值由式（14）和式（17）确定，然后假设加热功率，求解流动模型得到液膜分布进而得到充液率的计算值，充液率被定义为热管内的工质在液相时的体积占槽道体积之比，其计算方法如式（18）所示。 通过不断迭代调整加热功率的值，当计算充液率与设定充液率之差小于给定误差时，认为模型收敛，热管达到蒸发极限。 其中，由于热管被分为蒸发段、绝热段和冷凝段三部分，每一部分控制方程并不相同，因此每一部分末端的计算结果为下一部分的计算初值。 算法流程图如图4 所示。

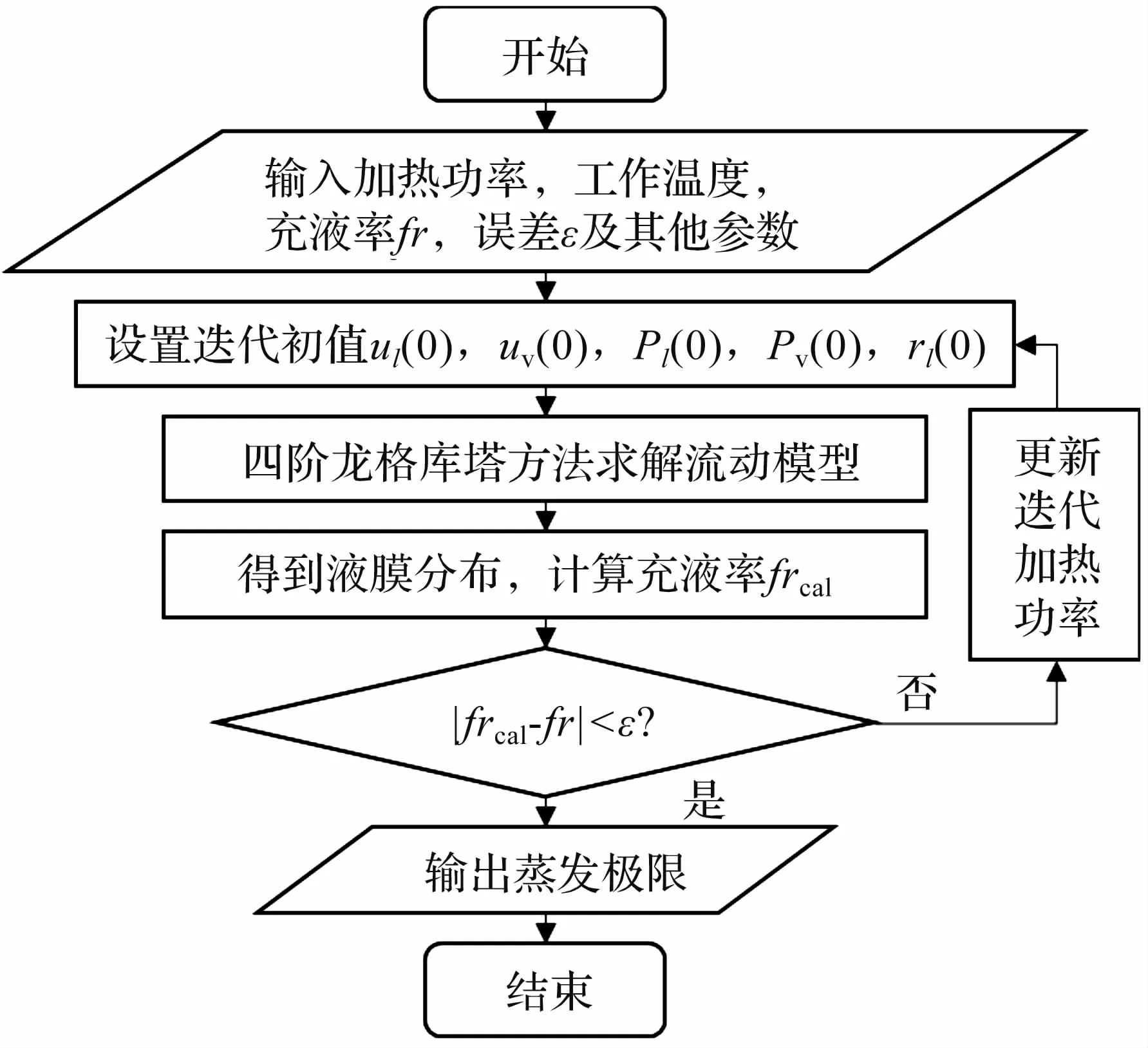
图4 蒸发极限计算流程图

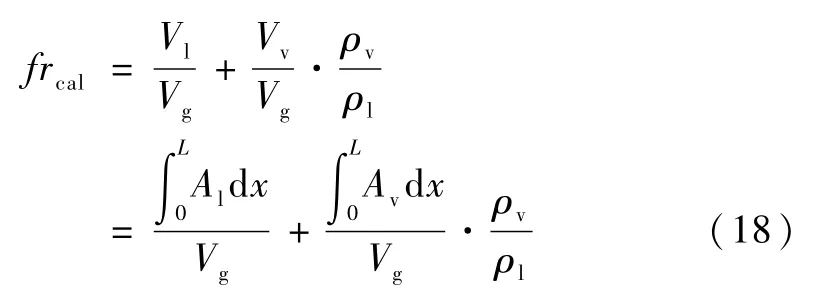
2.3 冷凝极限模型求解

本小节给出求解扁平微槽道热管冷凝极限的计算方法。 与蒸发极限的计算不同，冷凝极限需要求解含液堵段的方程组，由于本文认为液堵段长度等于冷凝段时，热管达到冷凝极限，因此，热管被分为蒸发段、绝热段和液堵段三部分。

我们无法确定在事先假定的加热功率下，热管是否会发生液堵，且液堵段长度等于冷凝段长度，因此，需要先求解不含液堵段的方程，确定液堵段长度，通过迭代加热功率使液堵段长度等于冷凝段长度，再求解含液堵段的方程组求得此冷凝极限所对应的液膜分布和充液率。

此外，冷凝极限是由于充液率过多导致冷凝段出现液堵，此时蒸发段不一定出现蒸干现象，因此蒸发段初始位置弯月面半径是未知的，不可能像求解蒸发极限时通过迭代调整加热功率来匹配充液率那样进行计算。

为克服上述困难，本文提出了一种遍历对比的方法求解冷凝极限，即针对一系列的弯月面半径迭代初值进行求解，得到一系列充液率和加热功率的对应组，然后针对相同充液率所得的所有加热功率取最小值作为其冷凝极限。 具体算法流程图如图5 所示。 需要指出的是，最后一步的判断计算充液率是否小于0.8 并无特殊意义，只是当充液率过大时，毛细极限较小，失去了计算的意义，因此选择较大的充液率值0.8 作为计算停止的条件。

3 结果与讨论

3.1 一维流动模型求解结果与讨论

图6 -图10 给出了一维流动模型在加热功率为5 W，充液率为20%、23%和26%时的计算结果，分别展示了铝—丙酮扁平微槽道热管液相速度、气相速度、液相压力、气相压力和弯月面半径沿热管轴向的变化。

从图6 可以看出，液相速度的最大值随着充液率的提升逐渐降低，这是由于充液率的增加导致液相体积增加，固液界面增加，使得剪切应力增加，从而使液相所能增加到的最大速度减小。 从图8 可以看出，随着充液率的增加，相同位置的液相压力逐渐增加，且沿轴向的总液相压力损失逐渐减小。 这是由于随着充液率的增加，液面逐渐平缓，使得热管初末位置的弯月面半径相差变小，由于气相压力基本保持恒定，根据Young-Laplace方程可知，液相压力沿轴向变化逐渐减小。 相同的趋势也可以从图10 中看出。

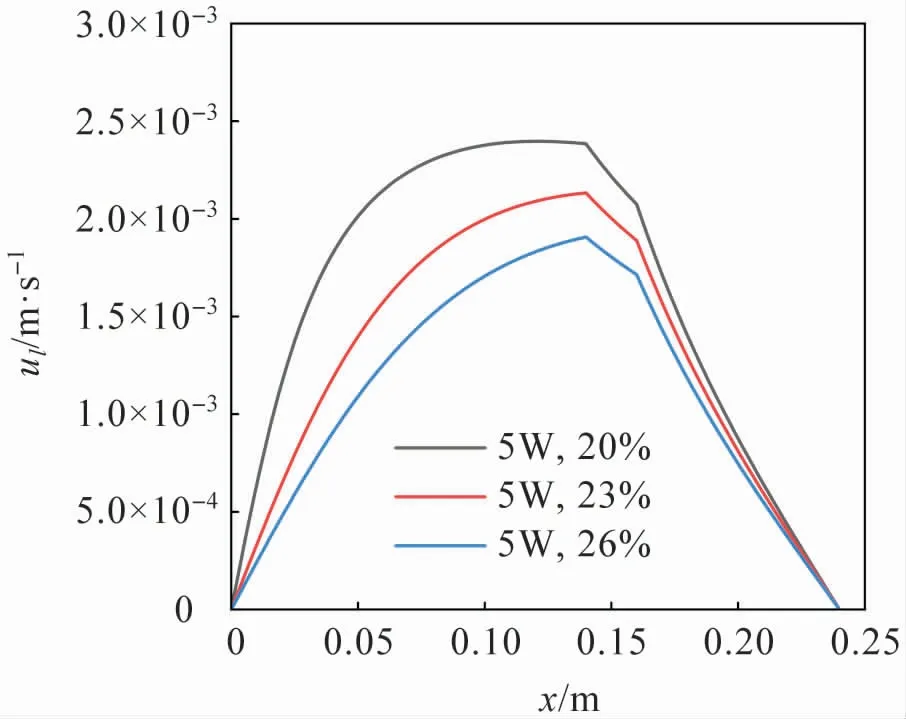
图6 液相速度沿热管轴向变化

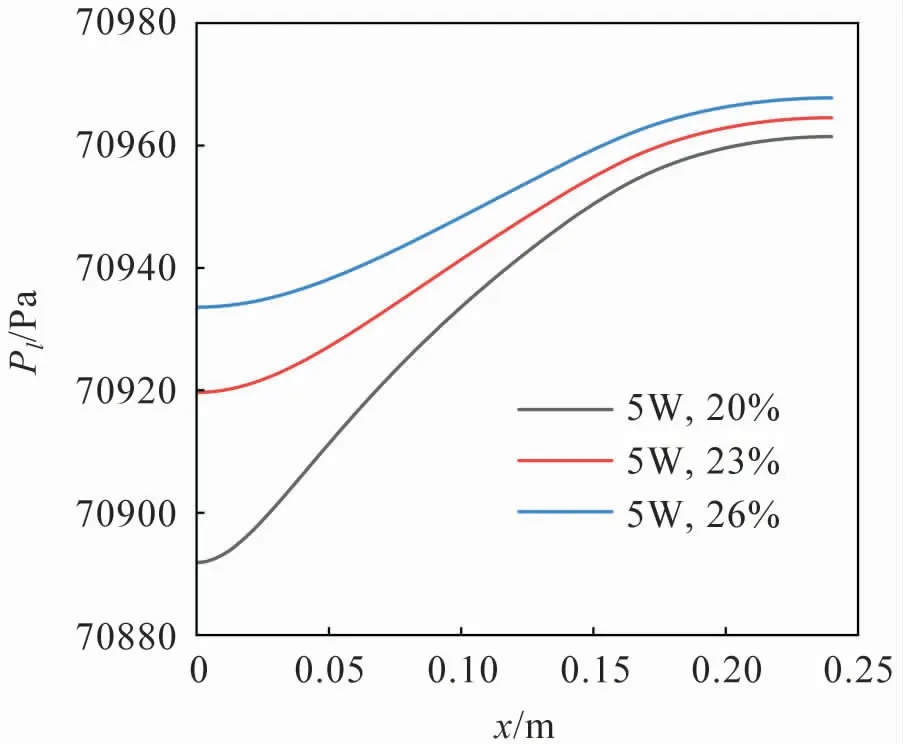
图8 液相压力沿热管轴向变化

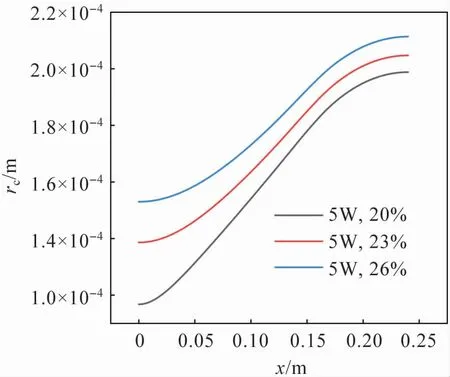
图10 弯月面半径沿热管轴向变化

图7 和图9 给出气相速度和压力随热管轴向距离的变化，可以看出，在同一加热功率下，气相参数随充液率的变化较小，这是因为在相同的加热功率下，热管的工作温度是基本相同的，这使得气相工质在相近的饱和温度下具有相近的饱和压力，进而具有相近的物性参数，得到相近的速度分布。

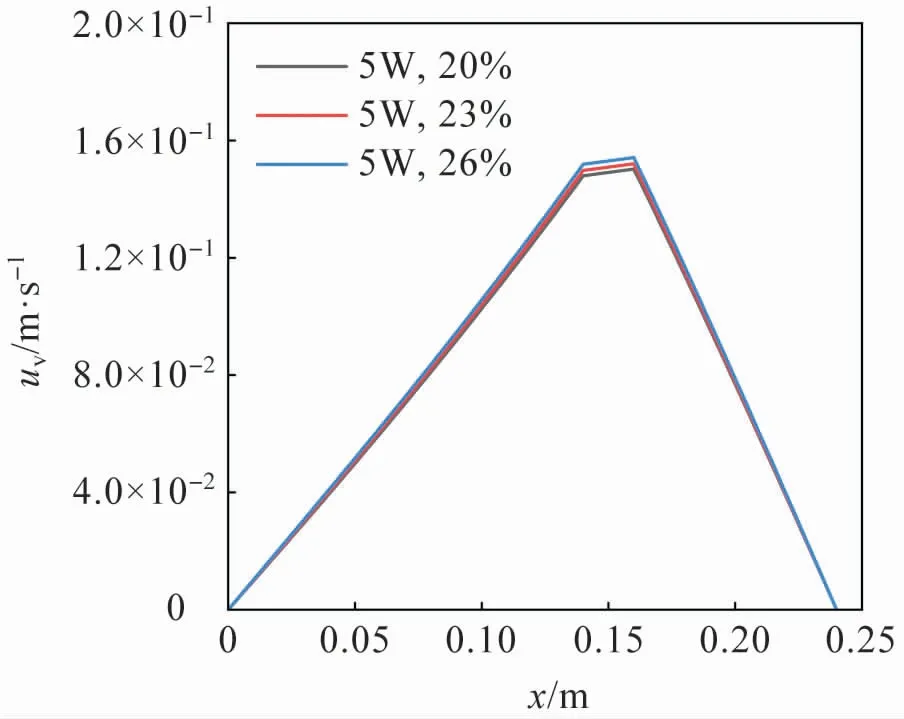
图7 气相速度沿热管轴向变化

图9 气相压力沿热管轴向变化

3.2 蒸发极限模型求解结果与讨论

图11 给出了所研究扁平微槽道热管蒸发极限随充液率的变化情况，可以看出，随着充液率的增加，蒸发极限逐渐增加，这是由于热管的蒸发段中含有更多的工质进行蒸发，可以带走更多的热量，避免蒸干现象的出现，进而提高热管的蒸发极限。

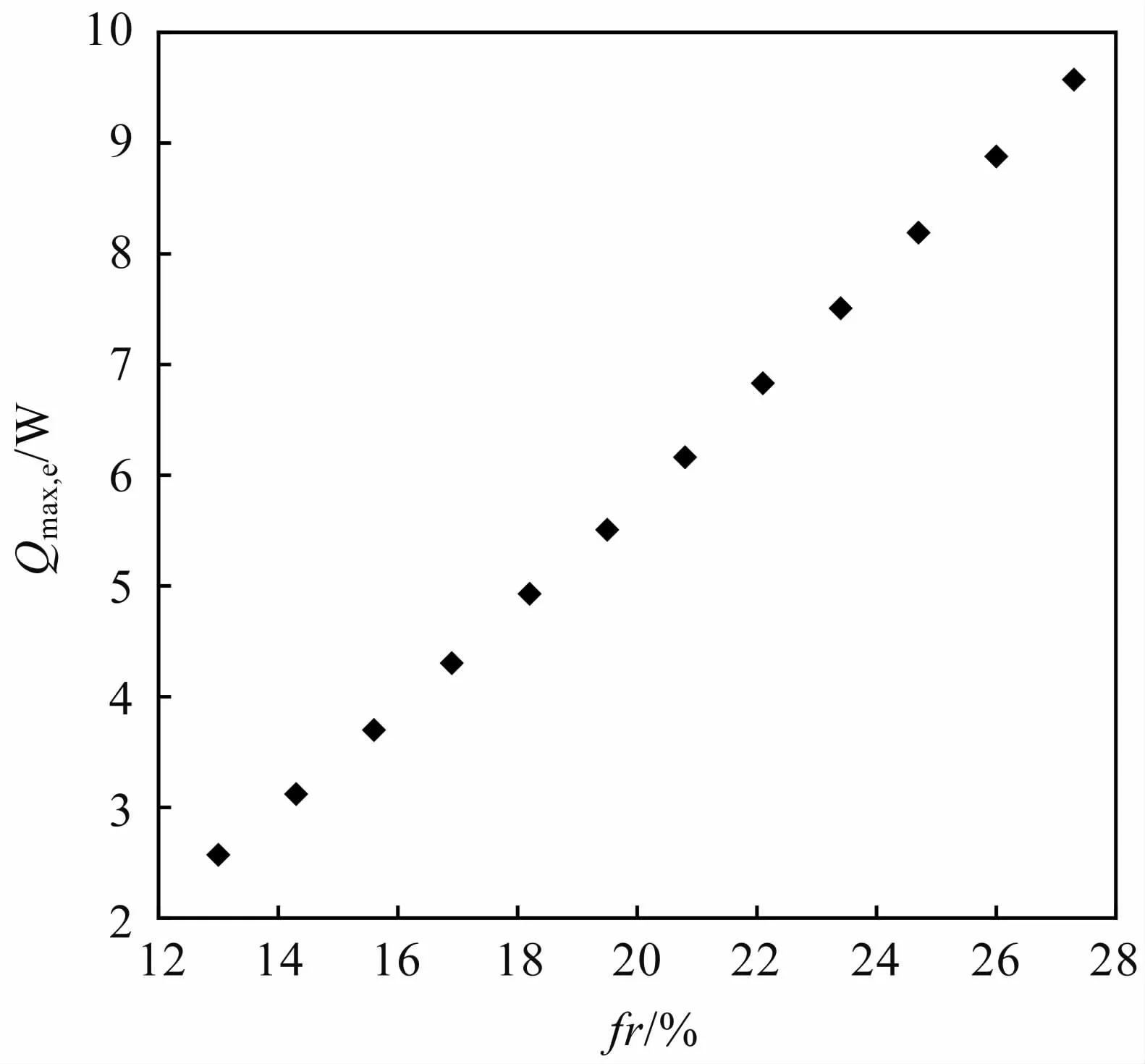
图11 蒸发极限随充液率变化

3.3 冷凝极限模型求解结果与讨论

图12 给出了所研究扁平微槽道热管冷凝极限随充液率的变化情况，可以看出，随着充液率的增加，冷凝极限逐渐降低，这是由于随着充液率的增加，冷凝段积累了更多的液相工质，液膜的增厚导致其导热热阻增加，进而使得热管整体热阻增加，传热性能下降。

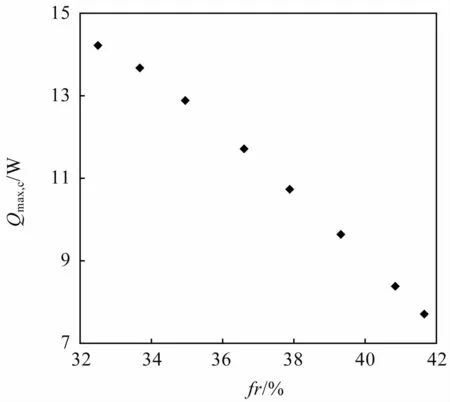
图12 冷凝极限随充液率变化

对比图11 和图12 可以发现，蒸发极限和冷凝极限的最大值之间有4W 左右的差距，且充液率之间也有8%左右的差别，这是因为该模型没有考虑冷凝段出现部分液堵段时的蒸发极限。 该极限的获得需要通过事先求解不含液堵段的方程确定液堵段长度，然后求解包含液堵段在内的四段方程组来获得，这将是今后的工作内容。 目前的模型可以说明，在现行结构下，扁平微槽道热管的最佳充液率在27% ～32%之间。

对于任意类似结构的扁平微槽道热管，均可以使用该模型对其充液率进行优化，得到热管最佳充液率，或者其对应的毛细极限，这对于特定工况下选择适当热管具有重要指导意义。

4 结 论

本文提出了一种基于一维流动模型的铝—丙酮扁平微槽道热管毛细极限模型，同时考虑了由于蒸发段蒸干导致的蒸发极限和由于冷凝段液堵导致的冷凝极限，在液堵段考虑了接触角的变化，并以此探究充液率对热管性能的影响。 计算结果表明：

（1）在相同加热功率下，随着充液率的增加，液相流动损失增加，液相回流最大速度减小，弯月面趋于平缓，充液率对气相参数影响较小；

（2）随着充液率的增加，蒸发极限逐渐增加；

（3）随着充液率继续增加，蒸发极限不会达到，冷凝开始下降；

（4）所探究热管毛细极限在14 W 左右，相应的最佳充液率在27% ～32%之间。