磁流变抛光过程粒子行为仿真分析
曹建国,张静静,张勤俭
(1.北京信息科技大学机电工程学院,北京 100192;2.北京交通大学机械与电子控制工程学院,北京100044 )
近年来,随着物联网新应用和5G 通信技术对各种传感器及低功耗、小尺寸芯片的需求增长,半导体晶圆市场的容量呈现爆发式增长。无论是制作集成电路还是功能器件,都要求晶圆具有极佳的平整度和超光滑表面,否则将直接降低产品性能[1-2]。目前,人们普遍采用化学机械抛光实现晶圆的超光滑加工。这种方法可获得较好的表面精度,但在实际应用中也显现出一定的缺点,例如:半导体晶圆为典型的硬脆材料,抛光过程中较大的机械力易造成其表面出现脆性破坏、裂纹、碎片等缺陷,同时晶圆较薄易翘曲变形;抛光后的工件表面会残留抛光浆料,难于清洗,而化学抛光浆液的后续处理会对环境带来负担,因此迫切需要一种满足低损伤、低应力、高效率、高质量加工的方法。
磁流变抛光方法是将用于抛光的磨料添入磁流变液,通过外加磁场,使磁流变液形成一定的柔性凸起,进而通过磁流变液对工件产生剪切力来实现对工件的磁流变抛光[3-5]。该方法凭借其适合平面抛光、抛光质量高以及成品率高等特点成为超精密加工领域的热点[6-7]。磁流变抛光技术是一种新型的确定性抛光技术,在无外加磁场时,磁性微粒无规则分布,磁流变液为可流动液体状态;在外加磁场作用时,磁性微粒呈链状分布,其流变特性急剧转变(毫秒级),表现为类似固体的性质;撤除磁场后,磁性微粒又会立刻恢复原液体性质[8]。利用磁流变液在梯度磁场下形成Bingham 流体与晶圆直接接触,通过相对运动实现晶圆表面的材料去除,可实现微纳米级表面的加工制造。
在精密抛光加工过程中,晶圆表面材料去除量及平坦度与晶圆表面作用力和抛光粒子速度分布密切相关[9],因此开展磁流变抛光过程中的晶圆表面压力及粒子速度分布研究具有重要意义。Prabhat Ranjan[10]采用FEA-CFD 仿真分析了化学机械磁流变抛光(CMMRF)过程中磁流变液与工件表面的接触行为。王翱翔[11]针对磁场辅助电化学机械研抛,利用有限元ANSYS 软件分别进行了流场仿真和电磁场仿真,但是并未对流场和电磁场进行耦合仿真,其结果可能与实际情况相差较大。董敏[12]仿真建立了磁流变动压效应下磨粒及磁性粒子的受力模型,但在计算过程中没有考虑磁场作用,仿真模型因简化带来了各种影响和误差。李旭[13]在微观角度上研究了磁流变弹性体的力-磁耦合行为,考虑铁磁颗粒的磁化特性,模拟结果与实验结果吻合良好。
若要揭示半导体晶圆磁流变抛光过程材料去除机理,促进磁流变抛光技术在半导体晶圆平面抛光的应用,需要更一步明确抛光过程晶圆表面作用力和粒子行为,为此本文建立了磁流变抛光过程中的宏观磁流变液抛光物理量的数学模型,采用有限元ANSYS 软件实现对磁流变抛光中磁场和流场的耦合模拟分析,重点研究了电磁场和抛光工艺参数对晶圆表面作用力及粒子速度分布的影响规律。
1 磁流变抛光液固两相流数学模型
在磁流变抛光过程中,磁流变液和铁磁颗粒流动满足质量和动量守恒。铁磁颗粒与液体无质量交换,二者的基本控制方程可表示为:
(1)连续性方程

式中:α 为各相的体积份额;u 为流体速度;ρ 为各相密度;下标k 为l 时指液相、为P 时指固相。
(2)液相动量方程
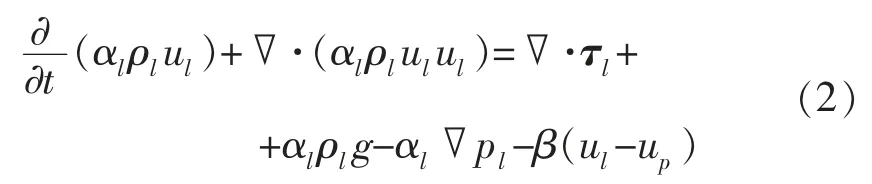
式中:g 为重力加速度;τl为液相应力张量;pl为液相压力;β 为液固两相间的动量交换系数。
液体的应力张量τl的表达式为:
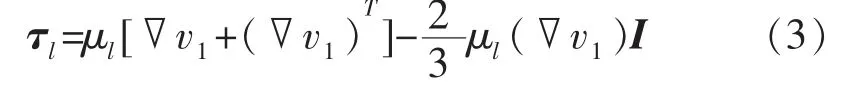
式中:I 为单位向量。
(3)固相动量方程

式中:Fm为颗粒所受磁场力。不考虑颗粒的磁化及磁致伸缩效应,依据Jackson 的结论,Fm为:

式中:Vp为粒子体积;μ0为真空磁导率,一般取4πe-7;χe为铁磁颗粒的磁化系数;H为磁场强度。
固相应力张量τp的表达式为:

式中:pp为固相压力;ξp为颗粒相动力粘度;μp为颗粒相剪切粘度。
固相压力pp的表达式为:

颗粒相动力粘度ξp的表达式为:

颗粒相剪切粘度μp的表达式为:

式中:β 为液固相间阻力系数,可按Gidaspow[11]公式进行计算。

其中,Cd=0.44,Re≥1000。
Re 位颗粒雷诺数为:

液体与颗粒之间的相互作用力复杂,有曳力、附加质量力、升力和Basset(巴塞特)力等,一般情况下并不需要考虑所有的力[14],故本文不展开讨论。
2 磁流变抛光过程仿真
2.1 磁流变抛光基本原理
图1 是磁流变抛光原理示意图。可知,抛光前将磁流变抛光液注入抛光盘上,使抛光液均匀分布在抛光盘上;在抛光过程中,抛光头、抛光盘和励磁装置分别以nh、nd和nm的速度旋转,且抛光头沿着x轴方向以Vc的速度振荡,以及设定抛光盘表面和晶圆底部之间的工作间隙;改变从抛光盘底部到励磁装置的激励间隙,可调节抛光盘表面的磁通密度;磁流变液沿着磁力线磁聚集形成表观粘稠的Bingham 类固体;在固定间隙及晶圆与抛光盘的相对运动中实现材料去除。

图1 磁流变抛光原理示意图
2.2 建立仿真模型
在磁流变抛光过程中,磁流变液中的铁磁颗粒在经过磁场区域时会被磁化,受到磁场力作用形成磁链,磁链包裹磨粒对晶圆表面进行抛光作用,实现材料去除。抛光过程复杂,模拟未添加磨粒、忽略颗粒被磁化后,颗粒之间也会产生磁场力。将模型简化后,基于固液两相流的数学模型确定仿真抛光的物理参数,见表1。

表1 模拟参数
在初始状态下,磁流变液均匀分布在抛光盘和晶圆夹持装置组成的封闭运动空间内,在流体旋转和晶圆的配合旋转下完成抛光过程。仿真模型采用非结构网格划分,为了节省计算时间,本文在晶圆区域局部细分网格,其他区域采用粗网格,也得到了较好的网格质量,划分网格总数为1 445 104。
2.3 边界条件及数值求解
基于磁流变液Bingham 模型和不可压缩流体Navier-Stokes 方程,本文认为在抛光过程中磁流变液为粘性不可压缩流体。离散相为铁磁颗粒,连续相为磁流变液。虽然离散相铁粉粒子在抛光过程中的分布受到磁场作用集中在晶圆区域,但总体来说其分布较广,可选用欧拉模型或Mixture 模型,但欧拉模型与ANSYS 软件中的MHD 模型不兼容,因此本文选用Mixture 模型。另外,本文针对压力速度采用MRF 多参考系方法及SIMPLEC 耦合算法,针对流项采用二阶迎风格式对流场进行离散,取迭代步长10-4s。本文还参考建立磁场仿真模型[15],编写磁场数据文件并导入ANSYS 软件,通过用户自定义程序(udf)将铁磁粒子的磁场力加入动量源项,从而完成仿真。仿真路线及用户自定义编写程序流程见图2,磁场磁极分布见图3,磁场数据文件通过maxwell 仿真模拟导出编写。

图2 计算模拟流程图

图3 磁极分布示意图
3 仿真结果分析
3.1 速度分布
图4a 和图4b 分别是抛光盘表面和晶圆表面的速度分布云图。可见,抛光盘处的速度沿着径向由圆心向边缘线性递减,而晶圆表面的速度呈现非规律分布,这是由于晶圆自身的旋转速度和流场中流体速度相叠加的效果;液膜内部流场相较于表面边缘流场的速度分布更加均匀、跨度更小,这为流体把速度传递给离散的磨粒创造了有利环境,使得磨粒获得了持续稳定的动能输送,从而实现平坦化抛光工艺。
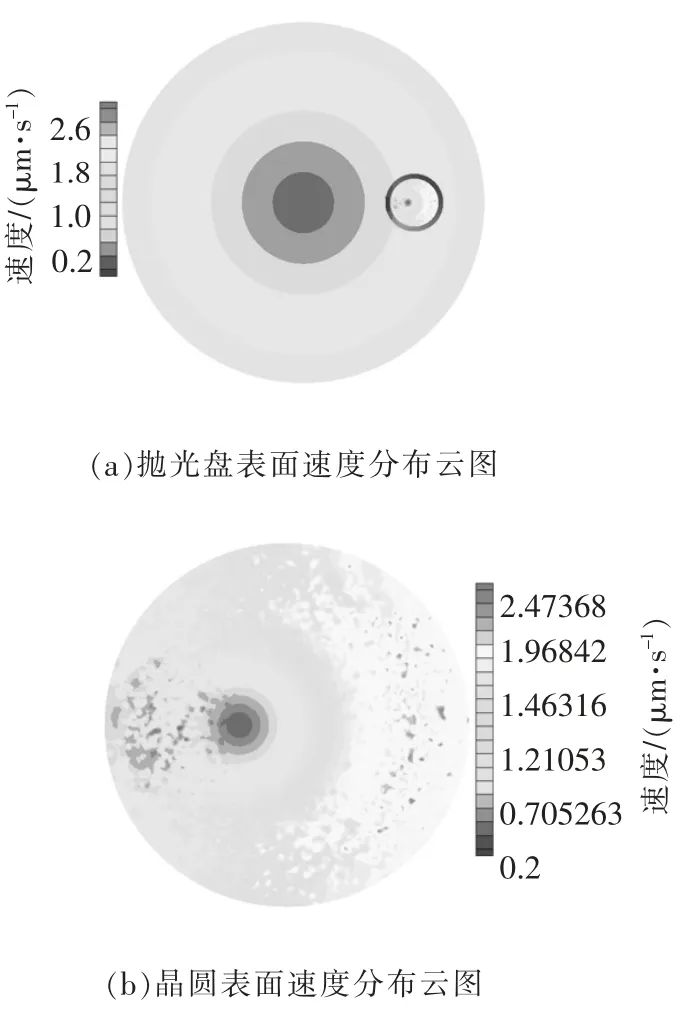
图4 抛光过程中速度分布
3.2 铁磁颗粒分布
磨粒的运动和分布规律是影响抛光平坦度和去除率的重要因素。实际工况中,磁流变液均匀分布在抛光盘上,将工件下压并与磁流变液接触而进行抛光加工,因此仿真计算时是假定初始状态下的铁磁颗粒均匀分布在抛光盘上。在磁流变抛光的稳态抛光过程中,铁磁颗粒的初始时刻在抛光盘及晶圆表面的分布分别见图5a 和图5b。在不添加磁场时,由于工件和抛光盘相对运动,粒子局部紊流,且粒子在工件表面的浓度较高,但分布并不均匀,在速度相对较高的区域,粒子浓度较大,在速度较低的区域,粒子浓度则相对较小。无磁场粒子分布如图5c 所示,粒子的分布状态是晶圆平坦化的重要影响因素,显然在无磁场时,粒子的分布状态并不满足于超精密加工的要求。

图5 抛光初始时刻粒子分布状态
在晶圆正下方,导入对应于图3 的集群式磁场数据文件后,铁磁颗粒受到磁场力作用,会出现一定的集聚现象,在抛光盘、晶圆相对运动及铁磁颗粒所受到的磁场力共同作用下,呈现图6 所示的不同铁磁颗粒粒径的晶圆表面粒子分布情况。可见,在磁场作用下,固相颗粒分布的不均匀区域有所减小,有效抑制了相对运动引起的紊流作用,颗粒在工件表面呈现较稳定的聚集状态,且在稳定抛光阶段,铁磁颗粒粒子的粒径越小,磁场力的把持作用越好,颗粒聚集的偏离度越小,更有利于晶圆表面抛光的效率和平坦度。分析原因是由于颗粒的粒径越小,对应的单颗颗粒质量也越小,在有相对运动的环境下,具有更小惯性的铁磁颗粒在磁场的作用下不易发生偏离。

图6 抛光过程不同铁磁颗粒粒径分布状态
3.3 晶圆表面作用力分布
3.3.1 压力分布
晶圆表面压力是由流体动压力和外部单位载荷共同作用的结果。在一定工况下,晶圆与抛光垫间形成一层含有很多磨粒的液膜,流动的抛光液裹夹着磨粒随之运动。由于待抛光晶圆的表面粗糙,存在很多微凸体,当移动的磨粒以一定速度通过晶圆粗糙面上的无数微凸体时,产生了动压作用。表面微凸体在无数磨粒周期性交变动压力的作用下产生破坏,从而实现材料去除。图7 是不同工况下的晶圆压力分布情况。可见,晶圆表面压力分布并不均匀,呈现递减趋势,但无磁场时的晶圆表面压力最高仅为300 Pa,有磁场时的晶圆表面压力平均达400 Pa;总体来看,有磁场时的压力分布相对更均匀,磨粒的粒径也更小。

图7 晶圆在不同情景的压力分布状态
3.3.2 剪切力分布
晶圆表面剪切力对材料去除率至关重要。图8是不同工况下的晶圆剪切力分布情况。可见,晶圆表面剪切力分布周向递增,剪切力与工件旋转速度密切相关;结合速度分布可得,速度越高,剪切力随之增加,晶圆中心部分的剪切强度最低,这也解释了抛光过程中晶圆的塌边现象。

图8 不同粒径下晶圆剪切力分布状态
由图9 所示的晶圆表面抛光力曲线可看出,相较于无磁场时的情况,添加磁场后的剪切强度有一定升高,晶圆边缘上升幅度最高为5 Pa;在晶圆中心点处,剪切强度最低不到2 Pa。随着铁磁颗粒粒径的增加,剪切力的变化并不明显,可初步判断剪切力的主要影响因素为晶圆表面的速度分布。

图9 晶圆中心线上的抛光力分布
4 结束语
基于多相流和离散相的考虑,建立了三维CFD磁流耦合模型,研究了不同工况下的晶圆和抛光垫间抛光液的速度、抛光磨粒和压力以及剪切力的分布规律。结果发现,在磁场条件下,磨粒分布、晶圆表面压力及剪切力分布和大小情况,相较于不添加磁场时,对晶圆表面去除的平坦度及去除率都有良好的促进作用,由此证实了磁流变抛光是相对于化学机械抛光更优的抛光技术。在铁磁颗粒粒径分别为100、200、300 μm 时,研究了三组工况的仿真抛光计算情况。结果发现,磨粒的粒径越小,磁场对磨粒的把持作用越好,由此可较好地将磨粒聚集在晶圆下方,从而有利于提高晶圆表面材料的去除率,并且磨粒的粒径越小,晶圆的表面压力分布也更均匀,更有利于晶圆的平坦化。

