基于扩张状态观测器的空间跟瞄转台指向控制方法

王语晨 康建兵 林喆 彭建军 许志炜

基于扩张状态观测器的空间跟瞄转台指向控制方法

王语晨1康建兵1林喆1彭建军2许志炜3

（1 北京空间机电研究所，北京 100094）（2 黄河上游水电开发有限责任公司格尔木分公司，格尔木 816099）（3 中国三峡新能源（集团）股份有限公司，北京 101199）

空间光电跟瞄系统对“远、暗、小、密”目标低速跟踪指向过程中，由于摩擦扰动、电机槽隙力矩波动扰动和传感非线性等因素，引发跟瞄转台低速爬行现象，导致瞄准误差增大，跟瞄成像抖动。针对这一问题，提出一种基于扩张状态观测器（Extended State Observer，ESO）的指向控制方法，在建立跟瞄转台矢量控制模型的基础上，提出双ESO复合控制方法，对引发跟瞄抖动和扰动的因素进行了在线观测与补偿。通过数值仿真对该方法的有效性进行验证，仿真结果表明，相比于传统比例积分（PI）控制方法与单转速环ESO方法，该方法可有效提高光电跟瞄转台在低速跟瞄时的跟瞄精度与平稳性。

指向控制 空间转台 双扩张状态观测器 永磁同步电机 光电跟瞄系统

0 引言

航空航天技术的迅速发展带来应用水平的不断提高，目前的技术水平已经能够将激光武器或光通信终端部署在临近空间至高轨等高远位置。在高远位置实施激光打击或进行激光通信具有观测范围大、不受地域限制等优点。星载激光通信是天地一体化激光通信网络的重要环节，已进入空间试验阶段，其链路类型包括星间、星空、星地、空地等，典型应用包括如图1所示的欧洲半导体激光星间链路实验（SILEX）计划、欧洲数据中继系统（EDRS）项目等[1-3]；天基激光武器涉及空间安全问题，具有尖锐的敏感性，各国往往将天基激光武器试验隐藏在相关科学研究项目中进行，美国从20世纪80年代就开始了天基激光武器的研制，走在世界前列，虽2013年后暂无公开报道[4-5]，但其关于天基激光武器的研究从未中止，当前很多具备战略打击能力的项目都有着较为深厚的相关背景。空间跟瞄转台作为确保激光光束完成精确跟瞄的核心组件，提升其跟瞄精度，减少跟瞄抖动，对确保天基激光装备的应用效能具有重要意义[6]。

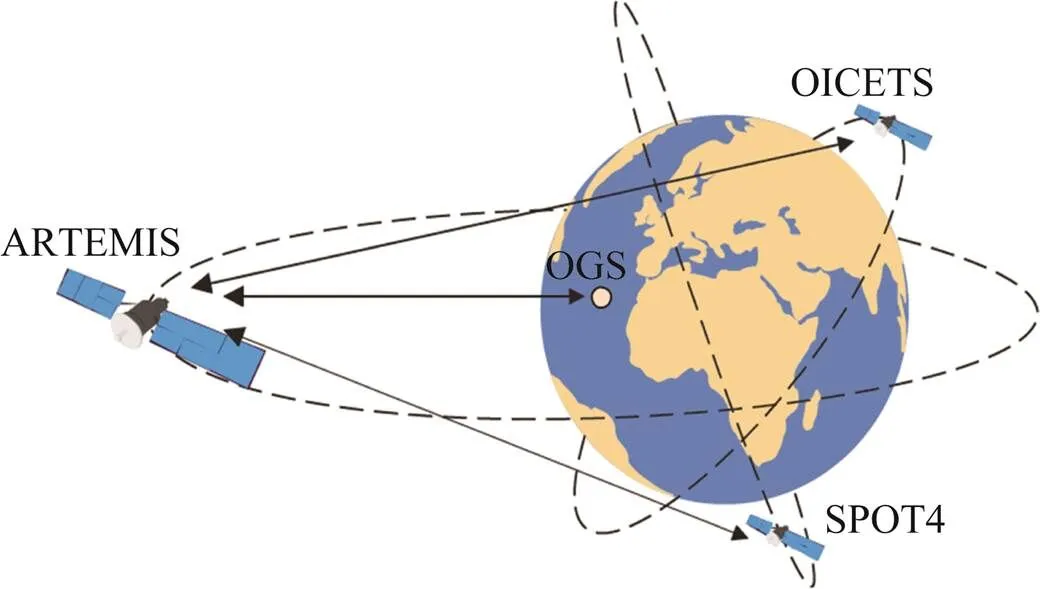
图1 SILEX项目示意

然而，对于距离较远的目标，几何关系变化小，跟瞄转台常处于低速或超低速运行状态，此时跟瞄转台受到摩擦力矩、波动力矩、传感器测量误差等非线性扰动的影响显著，在超低转速运行时转速会出现一快一慢的“低速爬行”现象[7-8]，使转台低速运行的平稳性变差。特别的，对于空间光电跟瞄系统，会受到外部空间环境扰动的影响，例如：低轨道卫星受到地球引力的影响，地球同步轨道卫星受到来自于太阳、月球等其他天体的引力影响，此外，太阳辐射、热形变和微小碎片也是常见的星载平台外部扰动源；卫星平台的内部扰动则主要来自自身的机械运动，包括推进器运动、天线转动以及太阳翼运动等，这些操作都会对空间光电跟瞄系统造成扰动，并且这些随机扰动很难建立数学模型。在实际应用过程中，质量不平衡力矩、装配误差等的不确定性，同样难以建立数学模型[9-10]。因此，改善跟瞄转台伺服系统的低速性能成为制约光电跟瞄系统性能的难点之一[2]。

近年来，为了改善跟瞄转台的抗扰性能，不少学者将滑模变结构[11]、模型预测控制[12]、模型参考自适应等一些新颖的方法应用到解决“低速爬行”问题中，例如：文献[13]针对编码器的有限转速分辨率引起转速振荡的现象，提出了一种基于跟踪微分器的转速估计器，并讨论了相关的参数整定方法；文献[14]给出了转速环和位置环基于变增益趋近律的滑模变结构设计方法；文献[15]提出一种迭代二次规划方法来处理由输入–输出反馈线性化导致的非线性约束，实现非线性模型预测控制，仿真结果表明该方法能够抑制参数变化和负载扰动产生的不良影响；文献[16]对传统的分段连续LuGre模型进行修正，导出了一种新的连续可微非线性摩擦模型，然后提出了一种自适应反推控制器，用于液压系统的精确跟踪控制，以处理参数不确定性和非线性摩擦补偿。这些方法均能够从不同角度提升系统的控制性能，但由于系统不可避免地存在难以精确建模的部分，部分扰动具有时变特性，系统实际上会受到未建模动态的影响，同时空间光电跟瞄系统所面临的空间环境不同于地面，存在着更多动力学不确定性。高精度跟瞄系统需要充分考虑未建模动态的影响，上述方法在这方面存在一定的局限性。因此，需要寻找一种适合空间光电跟瞄系统的控制方法，在被控对象无法做到精确建模时，满足空间光电跟瞄系统跟瞄转台低速工况下高精度、高平稳性的性能要求。

扩张状态观测器（Extended State Observer，ESO）的思想是将扰动、不确定性和未建模动态集中在一起，使用观察机制来估计总扰动。扩张状态观测器能够利用系统的输入、输出信号，实时估计出闭环控制回路中的总扰动，再利用观测得到的总扰动进行补偿。ESO的优势在于可以在不知道系统任何模型信息的情况下观测出总扰动的影响，从而降低了对系统精确建模的要求。但实际上系统中的信息也并非完全未知，这会导致对部分模型已知信息的浪费。本文针对跟瞄转台在超低转速运行时出现的低速爬行现象，提出了一种基于扩张状态观测器的指向控制方法，将跟瞄转台所受到的摩擦力矩、波动力矩、传感器量测噪声及参数摄动等扰动与不确定性共同视为总扰动；在永磁同步电动机（Permanent Magnet Synchronous Motor，PMSM）矢量控制的基础上，对电流闭环和转速闭环分别设计了扩张状态观测器，提出双闭环ESO复合控制方法，进行主动扰动抑制，并且考虑到了对模型已知信息的利用。数值仿真结果表明，该方法能够有效克服上述扰动与不确定性的影响，提高跟瞄转台在超低转速时的跟瞄精度和平稳性。

1 跟瞄转台建模与扰动分析

为了实现大角度、高可靠作动，空间转台多应用PMSM直驱形式。PMSM矢量控制[17]在旋转坐标系轴（轴与PMSM的转子磁链矢量的轴线重合，顺着转子旋转方向超前90°的电角度为轴）下的数学模型可表示为

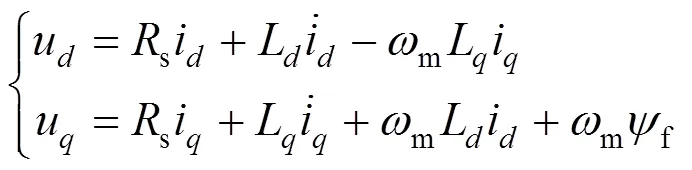
式中u和u分别为轴和轴施加的电压；s为电机定子绕组电阻；L和L分别为轴和轴电感；m为电机输出的机械角速度；i和i分别为轴和轴的电流；f为转子磁链。

电磁方程与电机运动方程如式（2）、（3）所示：

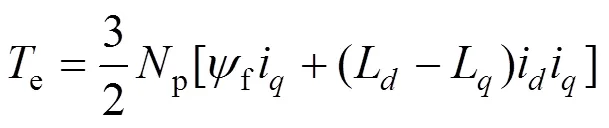
其中，p为电机极对数；为转子转动惯量；e、L、f分别为电磁转矩、负载力矩、扰动力矩；表示时间。PMSM矢量控制系统中m与i存在串级关系，i与i，m共同控制电机转速，存在动态耦合关系，假设采用表贴式PMSM，则有L=L。设1，2，3，4分别表示m，i，i以及电机转角m的状态变量，由式（1）～（3）可推导出PMSM矢量控制的状态空间方程，具体公式为

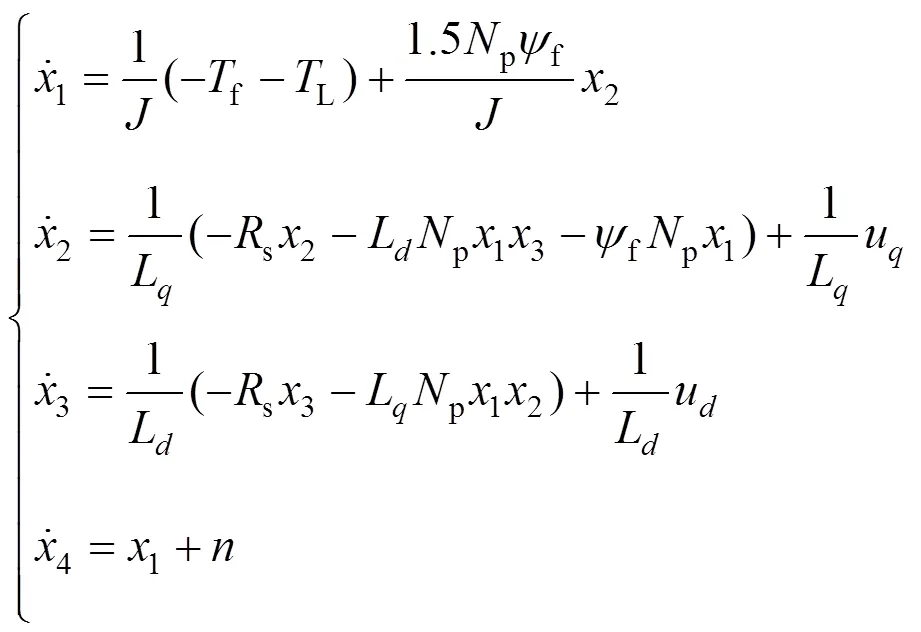
式中为传感器测量噪声（编码器测角误差）。

实现高精度、高平稳性控制要求的难点在于对扰动力矩的建模。根据学者的研究，在低速区间空间光电转台的轴系摩擦近似满足斯特里贝克（Stribeck）模型，该模型可表示为

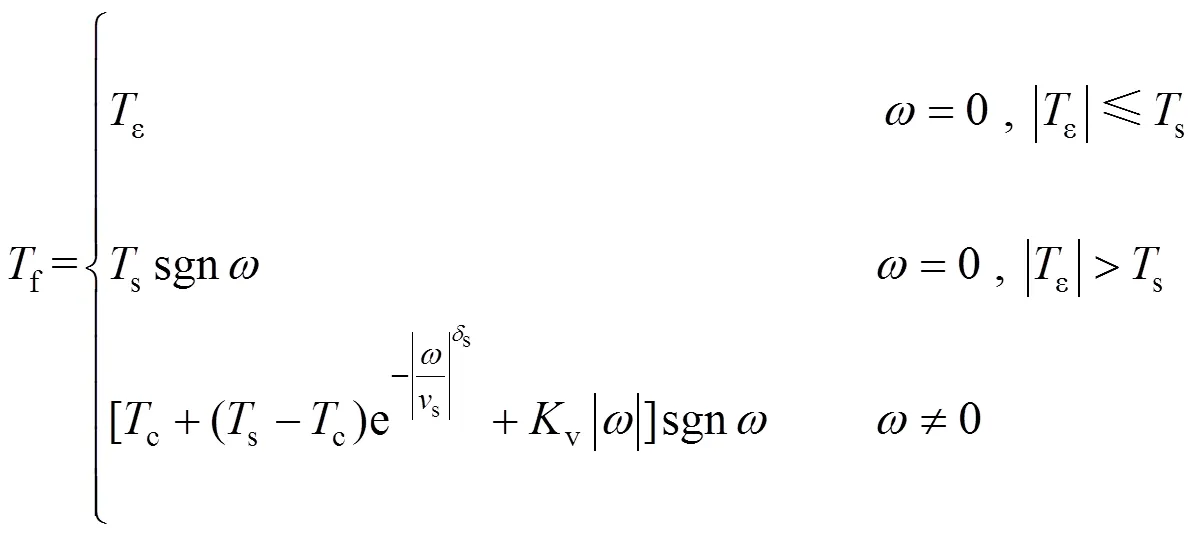
式中 Ts最大静摩擦力矩；Tε为外力矩；sgn为符号函数；Tc为库仑摩擦力矩；δs为经验参数；υs为Stribeck速度；Kv为粘滞摩擦系数；ω为电机转速。Stribeck曲线如图2所示，当转台在低速区间运行时，随着速度的增加，摩擦力矩将以指数的形式从静摩擦连续过渡为库仑摩擦[18-19]。

跟瞄转台控制系统通常采用三闭环控制结构，从内到外分别为电流环、转速环、位置环，采用i=0的电机控制策略。控制器常采用比例–积分–微分（PID）方法。利用Stribeck摩擦模型描述非线性摩擦力矩f，作为转矩输入端的主要扰动，c表示上述其他不确定性的部分，同时在角度信号输出端加入作为传感器测量噪声（编码器测角误差），控制流程如图3所示。

图3 跟瞄转台PID控制流程结构

传统的PID控制方法虽然具有简单易操作的优点，但是在其设计过程中，仅考虑了标称的线性模型，而当系统于低速运行时，非线性因素的影响加强，与设计PID控制器所考虑的标称线性模型差异显著，进而导致控制性能大幅退化。

2 基于ESO的双闭环复合控制方法

2.1 扩张状态观测器原理

扩张状态观测器最早由韩京清[20]提出，不少学者对该理论进行了深入的研究，ESO理论得到了进一步发展[21-24]。ESO基本思想是将总扰动扩张成系统的一个新的状态变量，然后用系统的输入和输出重构出包含系统原有状态变量与扰动的所有状态。设一个带未知扰动的非线性不确定系统为：

式中()为系统中未知的作用量；1，2，···，ξ–1，ξ为系统的状态变量；为控制量增益；为系统控制量；为系统输出；()为系统状态变量1，2，···，ξ的线性组合。设加速度的实时作用量为()(1,2, ···,ξ–1,(),)，在系统满足可观测性条件时，不论()形式如何，只要起作 用就必然会在输出上有所体现。ESO实际上就是从系统输出中提炼出()的一种具体方式，其一般形式为：

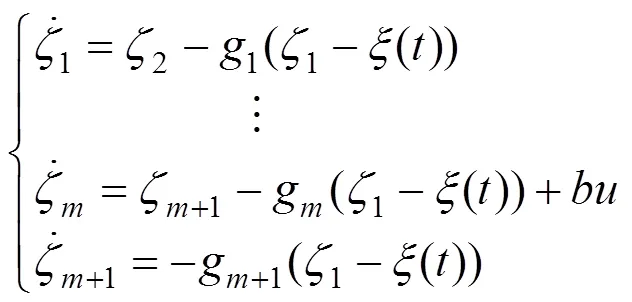
式中ζ为辅助变量，有1→1()，2→2()，···，ζ→ξ()，被扩张的状态量ζ+1→(1,2,··· , ξ–1,(),)；g(·)为非线性函数，=1，2，···，+1。显然，ESO设计时仅需要原系统的输入信息和输出信息，无关系统中未知函数的具体形式。

2.2 双扩张状态观测器复合控制

2.2.1 转速环扩张状态观测器设计

将式（4）中的转速环表达式改写为：

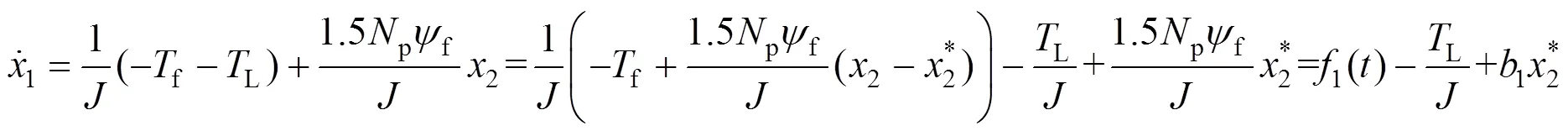
式中1()为表示转速环扰动、转速环非线性环节的抽象函数；2*为电流环的参考输入电流；1为转速环控制增益。设计转速环扩张状态观测器以消除1()中所包含的摩擦力矩、波动力矩、传感器测量误差等扰动及不确定性的影响，将电机的负载力矩作为模型的已知信息处理。

转速环ESO的输入为电机的量测转角经过差分后得到的转速和电流环的参考输入电流2*，其中非线性函数选取fal函数（如式（9）所示），该函数具有“小误差大增益、大误差小增益”的特性，能够避免高频颤振现象发生。根据式（8），建立转速环ESO的具体表达式，如式（10）所示。

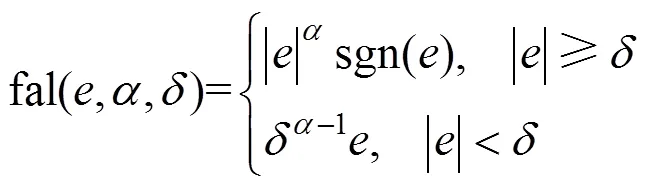
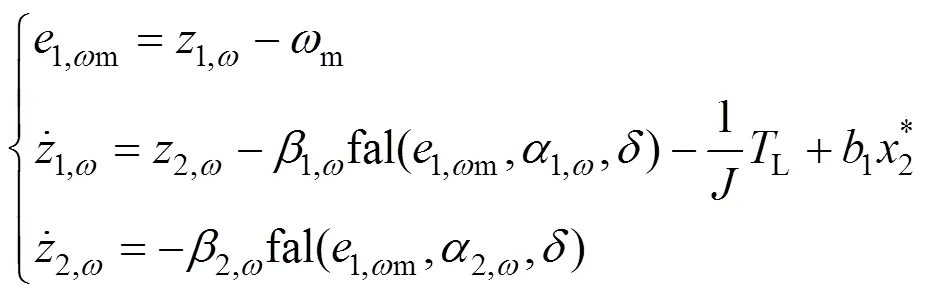
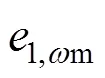
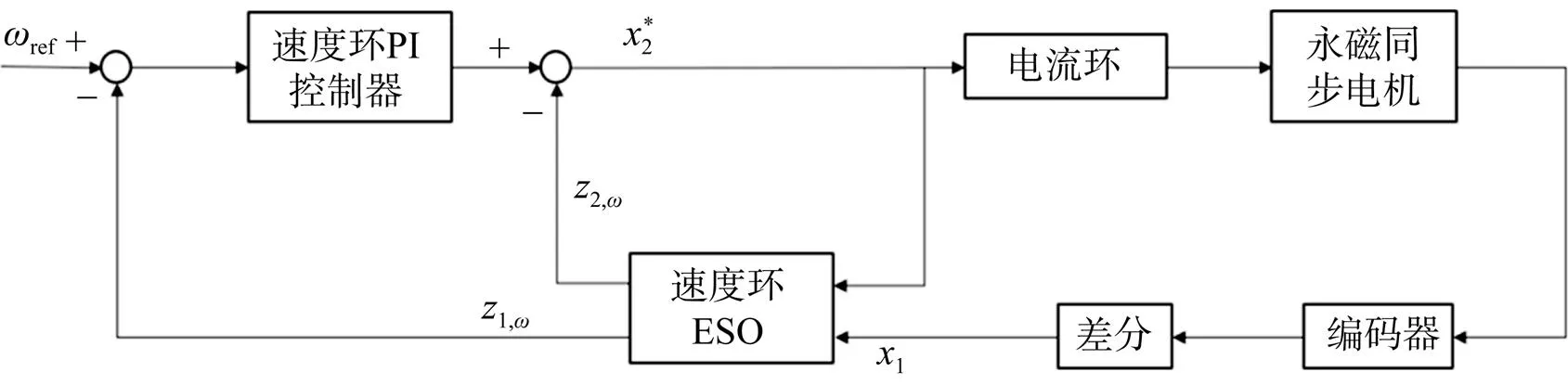
图4 扩张状态观测器改进转速环控制结构

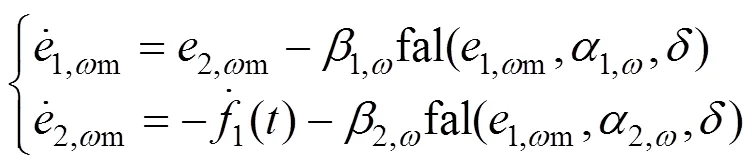
假设扰动是有界的，那么当观测误差的导数为零时观测器收敛，则观测误差可表示为

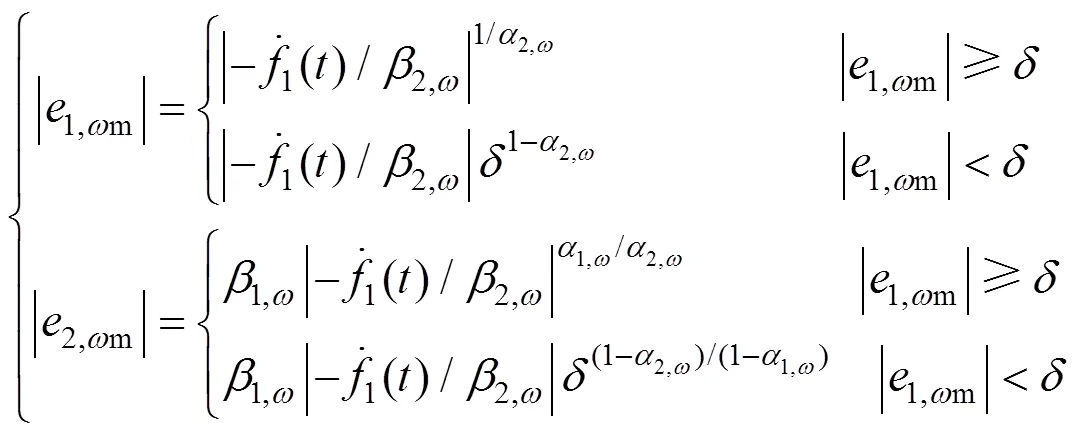
由式（12）可见，只要ESO的参数选择合理，误差就会收敛在一个足够小的区间内，观测误差将会收敛到所观测的状态量附近。

需要指出的是，电流环的非线性影响由转速环扩张观测器进行估测与补偿，这种方法虽然简化了控制设计，但未能直接从驱动角度进行观测，导致估测与补偿的精度不足，难以提升低速工况的PMSM的控制性能。

2.2.2 电流环扩张状态观测器设计

将式（4）中的电流环表达式改写为：

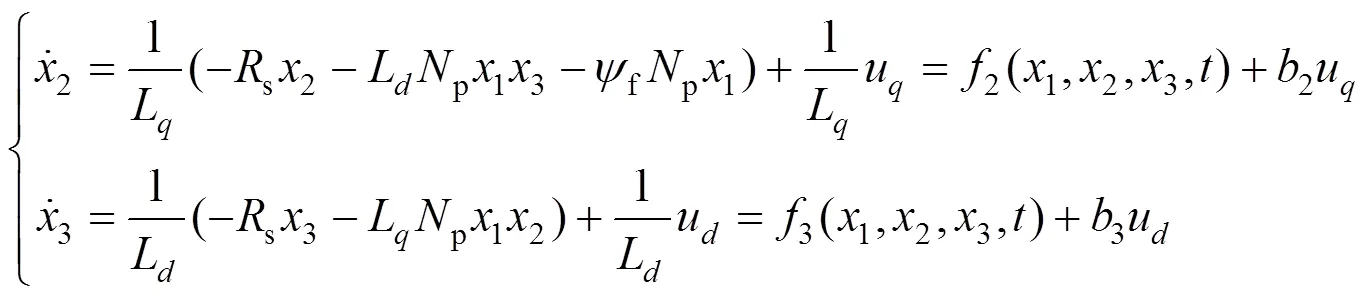
式中2(1,2,3,)，3(1,2,3,)分别表示电流环扰动、电流环非线性环节的抽象函数；2，3分别为、轴电流环控制增益。根据式（13）建立电流环ESO，如式（14）～（15）所示。电流环ESO的输入为电机输出电流由自然坐标系经过坐标变换到同步旋转坐标系的电流i、i，以及PMSM的输入电压u、u。

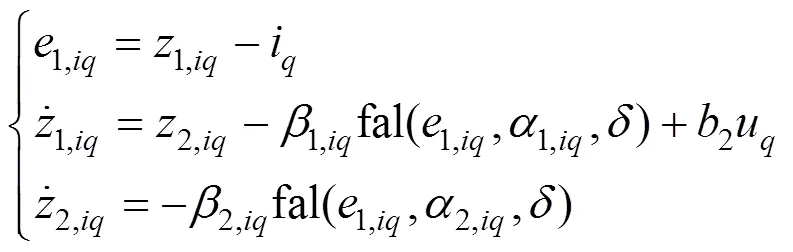
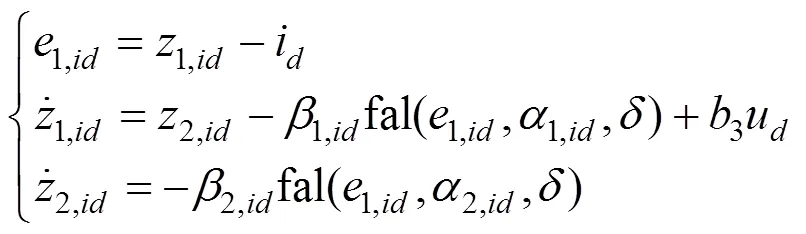
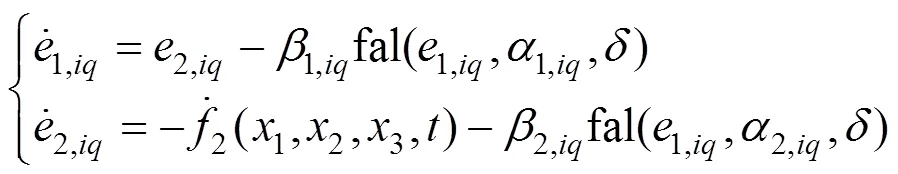
因此，只要观测器参数选取合理，误差就会收敛在一个足够小的区间内，z1,iq，z2,iq会收敛到观测的状态量附近。同理可证得：当d轴电流环ESO的观测器参数选取合理，误差会收敛在一个足够小的区间内。

基于位置、转速、电流三环控制，综合上述设计的转速环ESO与电流环ESO，得到双ESO复合控制方法，其控制结构如图6所示。

图6 双扩张状态观测器复合控制结构

3 仿真分析

为了验证双ESO复合控制方法的有效性，对比传统PI控制设计仿真试验。仿真电机与Stribeck摩擦模型参数设置如表1所示。

表1 仿真电机与Stribeck摩擦模型参数设置

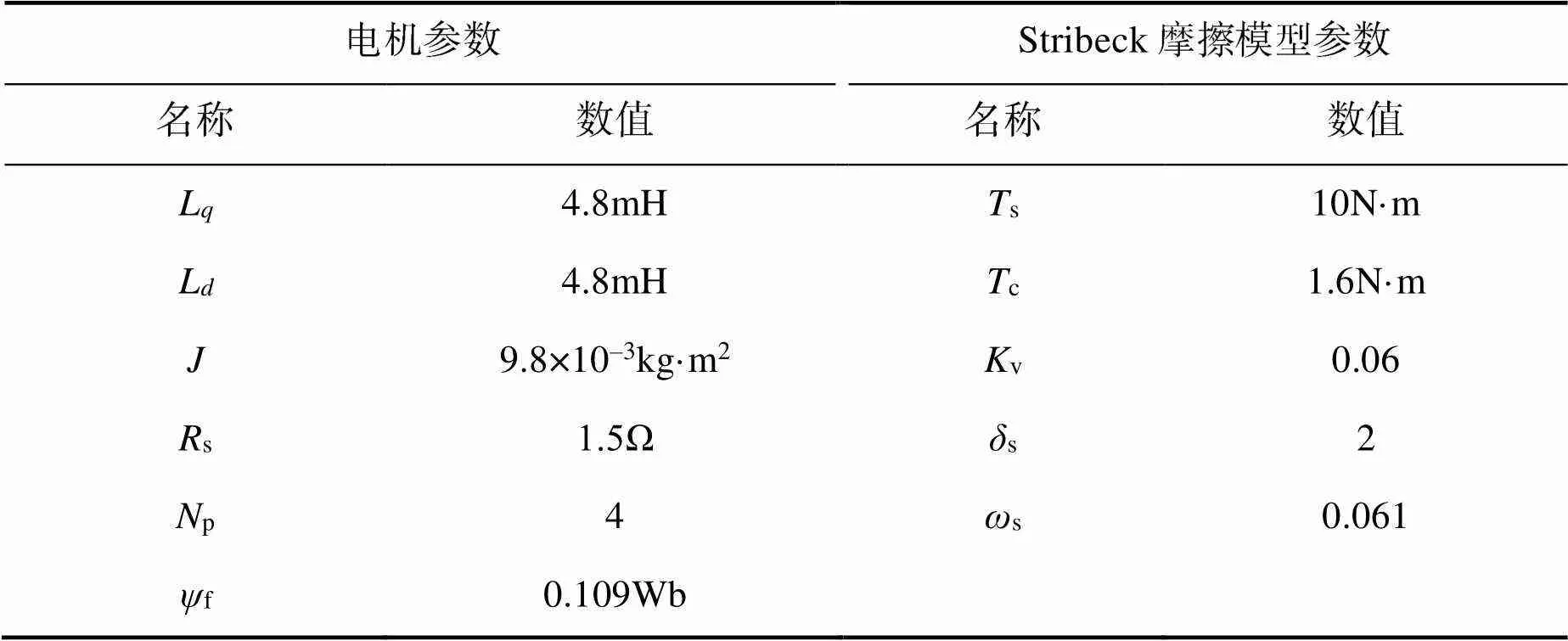
Tab.1 Simulation motor and Stirbeck friction model parameter settings

位置环、转速环、电流环比例积分（PI）控制器的比例、积分参数与ESO参数选取如表2～3所示。

表2 PI控制器参数设置

Tab.2 PI controller parameter settings

表3 ESO参数设置

Tab.3 ESO parameter settings

将0.36（°）/s斜坡输入、0.0382sin 20t正弦输入作为PI控制方法与双ESO复合方法的参考输入，电机负载力矩取L=20N·m，仿真结果的位置曲线、转速曲线、误差曲线分别如图7～9所示。由斜坡输入仿真结果可以得出，由于摩擦力矩、波动力矩与传感器测量误差作用，使系统出现了显著的低速爬行现象，在引入ESO后，能对干扰产生有效的抑制效果；由正弦输入仿真结果可以看出，当转速较低时，响应曲线的波形存在显著畸变，引入双ESO复合控制后，效果得到了明显的改善。

图7 0.36（°）/s斜坡输入，0.0382sin 20t正弦输入位置仿真曲线

图8 0.36（°）/s斜坡输入，0.0382sin 20t正弦转速仿真曲线

图9 0.36（°）/s斜坡输入，0.0382sin 20t误差曲线

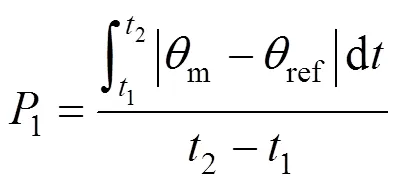
表4 斜坡输入与正弦输入时跟踪输入及平稳性能指标计算结果

Tab.4 Calculation results of performance index for slope input

由表4所列结果可见，在斜坡输入的情况下，ESO的引入能够将原系统的跟踪误差缩小37.2%，系统在非线性区间的平稳性提高65.5%；在正弦输入的情况下，ESO的引入能够使原系统的跟踪误差缩小10.4%，系统在非线性区间的平稳性提高86.4%。

将0.36（°）/s斜坡输入作为单转速环ESO方法与双ESO复合控制方法参考输入，电机负载力矩取L=20N∙m，两种方法仿真的转速曲线如图10所示。仿真结果表明，相比单转速环ESO方法，双ESO复合控制中电流环的引入能够进一步将转速的波动控制在0.1（°）/s范围内。

图10 0.36（°）/s斜坡输入时双ESO复合控制与单转速环ESO转速仿真曲线

4 结束语

本文针对跟瞄转台在超低转速运行时受摩擦力矩、波动力矩和传感器测量误差的影响而出现的“低速爬行”现象，提出了一种基于扩张状态观测器的指向控制方法。将跟瞄转台所受到的摩擦力矩、波动力矩、传感器噪声及参数摄动等扰动与不确定性分解为电流环与转速环的复合扰动。对电流闭环和转速闭环分别设计了ESO，采用双ESO复合控制策略，并进行主动扰动抑制。数值仿真结果表明，这种方法在对系统建模精度的要求较低时，仍然能够有效地提高系统的低速平稳性，与单转速环ESO方法相比，双ESO复合控制效果更佳。

本文提出的方法能够摆脱对被控对象精确建模的限制，并且充分利用了模型的已知信息，其控制性能优于传统PI控制方法。对于空间光电跟瞄转台动力学模型因环境因素发生变化，从而导致模型不确定性的问题，运用本方法能够对模型的不确定性有较好的补偿作用，因此适用于空间光电跟瞄系统。此外，该方法也为进一步利用扰动观测器方法实现精密仪器控制提供了方法和思路。但这种方法的缺点在于扩张状态观测器的参数复杂，存在调节困难的问题。

[1] 于思源. 卫星光通信瞄准捕获跟踪技术[M]. 北京: 科学出版社, 2016.

YU Siyuan. Pointing, Acquisition and Tracking Technology of Satellite Optical Communication[M]. Beijing: Science Press, 2016. (in Chinese)

[2] 姜会林, 安岩, 张雅琳, 等. 空间激光通信现状、发展趋势及关键技术分析[J]. 飞行器测控学报, 2015, 34(3): 207-217.

JIANG Huilin, AN Yan, ZHANG Yalin, et al. Analysis of the Status Quo, Development Trend and Key Technologies of Space Laser Communication[J]. Journal of Spacecraft TT&C Technology, 2015, 34(3): 207-217. (in Chinese)

[3] 王燕, 陈培永, 宋义伟, 等. 国外空间激光通信技术的发展现状与趋势[J]. 飞控与探测, 2019, 2(1): 8-16.

WANG Yan, CHEN Peiyong, SONG Yiwei, et al. Progress on the Development and Trend of Overseas Space Laser Communication Technology[J]. Flight Control & Detection, 2019, 2(1): 8-16. (in Chinese)

[4] 王明建, 范小虎, 黄雷. 国外天基武器系统及其关键技术[J].飞航导弹, 2014(8): 51-53.

WANG Mingjian, FAN Xiaohu, HUANG Lei. Foreign Space-based Weapon Systems and Their Key Technologies[J]. Aerodynamic Missile Journal, 2014(8): 51-53. (in Chinese)

[5] 伍尚慧. 美国高能激光武器最新发展现状及趋势[J]. 军事文摘, 2020(5): 40-44.

WU Shanghui. The Latest Development Status and Trend of American High Energy Laser Weapon[J]. Military Digest, 2020(5): 40-44. (in Chinese)

[6] LIU X D, ZHAO X R, CHEN Z. A PMSM Back-stepping Time-varying Sliding Mode Control System Based on Two-dimensional Spaceborne ATP Mechanism[C]//2016 IEEE Conference on Control Applications (CCA), September 19-22, 2016, Buenos Aires, Argentina. 2006: 249-254. DOI: 10.1109/CCA.2016.7587844.

[7] 张新邦, 曾海波, 张锦江. 仿真转台若干性能问题讨论[J]. 航天控制, 2017, 35(5): 64-67.

ZHANG Xinbang, ZENG Haibo, ZHANG Jinjiang. The Discussion on the Question of Servo Turntable Performance[J]. Aerospace Control, 2017, 35(5): 64-67. (in Chinese)

[8] 李婧, 张艾, 王淳. 空间望远扫描控制系统的电流环设计与仿真[J]. 航天返回与遥感, 2020, 41(5): 72-82.

LI Jing, ZHANG Ai, WANG Chun. Design and Simulation of Current Loop for the Space Telescope Scanning Control System[J]. Spacecraft Recovery&Remote Sensing, 2020, 41(5): 72-82. (in Chinese)

[9] ZHANG M, LIANG Y B. Compound Tracking in ATP System for Free Space Optical Communication[C]//2011 International Conference on Mechatronic Science, Electric Engineering and Computer (MEC), August 19-22, 2011, Jilin, China. DOI: 10.1109/MEC.2011.6025499.

[10] LI T, WANG S, ZHANG X. Space Tracking System and Its Key Technological Analyses[C]//2009 5th International Conference on Wireless Communications, Networking and Mobile Computing, September 24-26, 2009, Beijing, China. DOI: 10.1109/WICOM.2009.5304093.

[11] CUI N, ZHANG Q, WANG Q, et al. Sliding Mode Control Method of Photoelectric Turntable Based on LuGre Friction Model[C]//2019 22nd International Conference on Electrical Machines and Systems (ICEMS), August 11-14, 2019, Harbin, China. DOI: 10.1109/ICEMS.2019.8921673.

[12] 史涔溦, 解正宵, 陈卓易, 等. 永磁同步电机无参数超局部模型预测控制[J]. 电机与控制学报, 2021, 25(8): 1-8.

SHI Cenwei, XIE Zhengxiao, CHEN Zhuoyi. Model-free Predictive Control Based on Ultra-local Model for Permanent Magnet Synchronous Machines[J]. Electric Machines and Control, 2021, 25(8): 1-8. (in Chinese)

[13] LI L, PEI L, WANG F. Research on Speed Oscillation of Ultra-Low Speed Turntable in Aerospace Due to Limited Resolution Encoder[J]. IFAC-Papers on Line, 2019, 52(12): 322-327.

[14] 刘京, 邓永停, 李洪文. 基于级联滑模控制的高精度光电跟踪与捕获[J]. 光学精密工程, 2020, 28(2): 95-107.

LIU Jing, DENG Yongting, LI Hongwen. High Precision Photoelectric Acquisition and Tracking Based on Cascade Sliding Mode Control[J]. Optics and Precision Engineering, 2020, 28(2): 95-107. (in Chinese)

[15] 孔小兵, 刘向杰. 永磁同步电机高效非线性模型预测控制[J]. 自动化学报, 2014, 40(9): 1958-1966.

KONG Xiaobing, LIU Xiangjie. Efficient Nonlinear Model Predictive Control for Permanent Magnet Synchronous Motor[J]. Acta Automatica Sinica, 2014, 40(9): 1958-1966. (in Chinese)

[16] YAO J, DENG W, JIAO Z. Adaptive Control of Hydraulic Actuators With LuGre Model-based Friction Compensation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(10): 6469-6477.

[17] DENG F, GUAN Y. PMSM Vector Control Based on Improved ADRC[C]//2018 IEEE International Conference of Intelligent Robotic and Control Engineering (IRCE), August 24-27, 2018, Lanzhou, China. 154-158. DOI: 10.1109/IRCE.2018.8492927.

[18] WANG L, LI Q, JIAO R, et al. Tracking of Stribeck Friction Based on Second-order Linear Extended State Observer[C]//2016 Chinese Control and Decision Conference (CCDC), May 28-30, 2016, Yinchuan, China: 4334-4337. DOI: 10.1109/CCDC.2016.7531746.

[19] LIU L L, LIU H Z, WU Z Y, et al. An Overview of Friction Models in Mechanical Systems[J]. Advances in Mechanics, 2008, 38(2): 201-213.

[20] 韩京清. 一类不确定对象的扩张状态观测器[J]. 控制与决策, 1995(1): 85-88.

HAN Jingqing. Extended State Observer for a Class of Uncertain Objects[J]. Control and Decision, 1995(1): 85-88. (in Chinese)

[21] LI S, YANG J, CHEN W H, et al. Generalized Extended State Observer Based Control for Systems With Mismatched Uncertainties[J]. In IEEE Transactions on Industrial Electronics, 2012, 59(12): 4792-4802. Doi: 10.1109/TIE.2011.2182011.

[22] ZHAO S, GAO Z. Active Disturbance Rejection Control for Non-minimum Phase Systems[C]//Proceedings of the 29th Chinese Control Conference, July 29-31, 2010, Beijing, China, 2010: 6066-6070.

[23] IKEMOTO N, ISHIDA Y, MATSUMOTO N. Active Disturbance Rejection Control with Linear Quadratic Regulator for Non-minimum Phase Systems[C]//9th IEEE Control and System Graduate Research Colloquium (ICSGRC). [S.l: s.n.], 2018: 89-93. DOI: 10.1109/ICSGRC.2018.8657573.

[24] CUI R, CHEN L, YANG C, et al. Extended State Observer-Based Integral Sliding Mode Control for an Underwater Robot With Unknown Disturbances and Uncertain Nonlinearities[J]. In IEEE Transactions on Industrial Electronics, 2017, 64 (8): 6785-6795. DOI: 10.1109/TIE.2017.2694410.

A Pointing Control Method of the Space Tracking Turntable Based on Extended State Observer

WANG Yuchen1KANG Jianbing1LIN Zhe1PENG Jianjun2XU Zhiwei3

（1 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）（2 Huanghe Hydropower Development Co. Ltd., Golmud Branch, Golmud 816099, China）（3 China Three Gorges Renewables (Group) Co. Ltd., Beijing 101199, China）

In the low-speed tracking and pointing process of "far, dark, small and dense" targets in space photoelectric tracking and pointing system, the tracking and pointing turntable crawls at low speed due to friction disturbance, motor slot torque fluctuation disturbance and sensor nonlinearity, which leads to the increase of aiming errors and the jitters in tracking and pointing imaging. To solve this problem, a pointing control method based on Extended State Observer (ESO) was proposed. Based on the vector control model of the tracking and pointing turntable, a dual ESO composite control method is proposed to observe and compensate the factors causing tracking and pointing jitter and disturbance online. The effectiveness of the proposed method is verified by numerical simulation. Simulation results show that compared with traditional PI control methods and ESO methods, this method can effectively improve the tracking accuracy and stability of the photoelectric tracking turntable at low speed.

pointing control; space turntable; dual Extended State Observer; permanent magnet synchronous motor; photoelectric tracking system

TP272

A

1009-8518(2022)05-0078-12

10.3969/j.issn.1009-8518.2022.05.008

2022-02-21

国家自然科学基金（62227812）

王语晨, 康建兵, 林喆, 等. 基于扩张状态观测器的空间跟瞄转台指向控制方法[J]. 航天返回与遥感, 2022, 43(5): 78-89.

WANG Yuchen, KANG Jianbing, LIN Zhe, et al. A Pointing Control Method of the Space Tracking Turntable Based on Extended State Observer[J]. Spacecraft Recovery & Remote Sensing, 2022, 43(5): 78-89. (in Chinese)

王语晨，男，1998年生，2020年获大连海事大学测控技术与仪器专业学士学位，现在中国空间技术研究院精密光电仪器控制专业攻读硕士学位。研究方向为空间遥感器机构精密伺服控制技术。E-mail：wangyc_98@163.com。

（编辑：夏淑密）