几何形状对十字伞充气和滑翔性能的影响
黄云尧 武士轻 张扬,*
几何形状对十字伞充气和滑翔性能的影响
黄云尧1,3武士轻2,3张扬1,3,*
(1 南京航空航天大学航天学院,南京 210016)(2北京空间机电研究所,北京 100094)(3中国航天科技集团有限公司航天进入、减速与着陆技术实验室,北京 100094)
为了研究几何形状对十字伞充气和滑翔性能的影响,文章采用LS-DYNA软件中的结构化任意拉格朗日-欧拉(S-ALE)流固耦合求解器,利用数值仿真对5种不同几何形状的十字伞进行了动态开伞过程模拟,得到了十字伞展开过程中不同时刻的伞衣形状,并对不同伞型的充气性能进行了对比分析。此外,对充气稳定后的十字伞,通过在其伞绳端施加恒定载荷使其具备滑翔能力,并对比分析了5种伞型的滑翔性能。数值结果表明,异形结构对十字伞的充气性能影响较大,但对滑翔性能的影响因伞型而异,十字伞的长宽比对充气和滑翔性均具有较大影响。
充气性能 滑翔性能 十字伞 流固耦合 航天返回
0 引言
降落伞因具有质量小、减速效果好等优点,已被广泛应用于载人航天、登月返回、空降兵训练以及定点空投等重大航空航天任务。传统的空投系统容易受到风场等环境因素的影响,一经投放便无法对降落伞进行后续控制。在恶劣的天气条件下,空投行动要么无法实施,要么严重偏离预定着陆区,不仅降低了空投效果而且容易对地面人员及设施造成损坏[1]。
冲压式翼伞由于具备优良的滑翔性能和可操纵性,不仅可以通过自主归航控制实现载荷的精确定点回收,还可通过“雀降”操纵实现高效的安全无损着陆[2]。以翼伞为代表的精确空投系统(JPADS)[1]落点非常准确,但成本较高,原因是为翼伞提供高机动性的高性能减速器的制造需高昂的人工成本,同时为了能够承受伞衣打开过程中的巨大冲击力并提供足够的滑翔和转弯特性,所使用的材料也十分昂贵,加工难度大,这些因素导致基于翼伞的精确空投系统的研制成本相对过高[1]。传统的不受控系统虽然研制成本相对较低,但落点误差较大。因此,为了兼顾空投的准确性和经济性,一种利用现有技术来提供较为精确落点位置的低成本可控空投系统(Affordable Guided Airdrop System,AGAS)应运而生[1]。
最初的AGAS研究基于圆形伞,当前则主要针对十字伞[1]。与翼伞相比,十字伞的构造既简单又经济,且气动特性和机理的研究较为成熟;与标准的圆形伞、环帆伞以及其他类型的降落伞相比,十字伞的高几何孔隙率使其在自由来流和尾流区中能够更好地维持稳定性。高几何孔隙率虽然可能导致较大的下降速率,但由于减少了总的下降时间,可以在下降后迅速清理空域,并快速穿越未知或变化剧烈的风况[2]。虽然十字伞的控制能力与翼伞相比仍较为有限,但最近一些基于十字伞的研究发展出了各种各样的控制策略和手段,在应用于AGAS方面展现出了巨大的潜力[2-7]。
目前针对AGAS的研究主要有风洞试验、飞行试验以及数值仿真等手段。文献[4-5]利用NASA的6.096m垂直风洞对可控十字伞进行试验,发展出了一种可对十字伞航向稳定性进行控制和调整的控制器,并对5种不同几何形状伞衣的十字伞进行了风洞试验,比较了不同伞型的滑翔特性和落点精度,确定出能提供最佳落点精度的十字伞型;文献[6]通过飞行测试研究了标准型十字伞和混合型十字伞的滑翔性能,通过对十字伞的形状以及伞绳长度进行调整,达到控制十字伞的滑翔比和转弯性能的目的;文 献[7]利用LS-DYNA软件模拟了操纵十字伞的开伞过程,并通过对伞绳的长度进行调整实现控制的效果;文献[8]通过ALE(Arbitrary Lagrange-Euler)算法对十字型阻力伞的充气过程进行数值模拟,讨论了不同开伞速度、计算域网格密度等对阻力伞开伞动载荷的影响;文献[9]采用S-ALE(Structured ALE)算法对半折叠状态的十字型阻力伞的开伞过程进行仿真计算,分析了伞衣充气张满过程,获得了十字伞的阻力特性。
相对于风洞测试和飞行试验,数值仿真受不可控因素(如风速、气候)的影响较小,更改参数更为灵活,研究成本较低。因此,通过数值仿真研究十字伞的工作过程已逐渐成为一个热点,但目前大多是基于标准十字伞外形进行充气过程模拟[7-9],针对不同形状十字伞的充气和滑翔特性的相关数值仿真研究仍较为匮乏。本文将参照文献[5]中的垂直风洞试验研究,针对5种不同几何形状的十字伞,采用S-ALE方法仿真分析十字伞伞衣几何形状对其充气和滑翔性能的影响。
1 数值仿真方法
1.1 方法介绍
ALE方法最早出现于数值模拟流体动力学问题的有限差分方法中[10],这种方法兼具Lagrange方法和Euler方法的优势:首先,在物体边界运动的处理上引进了Lagrange方法的特点,能够使内部网格单元有效地跟踪物体边界的运动;其次,在内部网格的划分上,吸收了Euler方法的长处,使内部网格与物质材料相互独立存在,网格可以根据定义的参数在求解过程中适当调整位置,使得网格不至于出现严重的畸变。
S-ALE方法与ALE方法的理论完全一致,二者的区别在于S-ALE方法进行流场建模的方式与ALE方法直接进行网格划分不同,S-ALE流场域只需要设置三个维度的位置和网格数量,然后通过关键字对网格进行物质填充即可。S-ALE求解器是在ALE求解器的基础上发展而来,适用于结构化网格流固耦合问题的求解,在理论和算法相同的情况下,利用结构网格节点排序的规律性对ALE算法进行简化,通过关键字控制自动生成结构化网格,大大减少了计算时间和内存开销。
1.2 控制方程
在ALE方法的描述中,引入拉格朗日和欧拉坐标外的第三个任意参照坐标,则拉格朗日坐标下物体的运动可以描述为[11]:
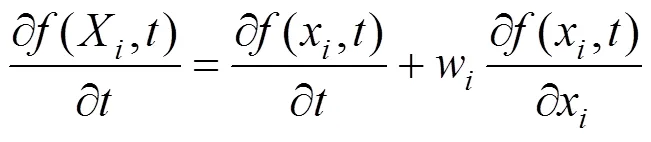
因此ALE算法的控制方程可以由质量、动量以及能量守恒方程给定,具体为:
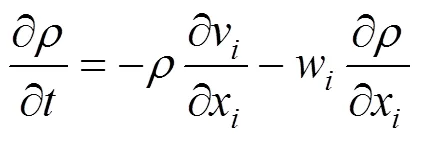
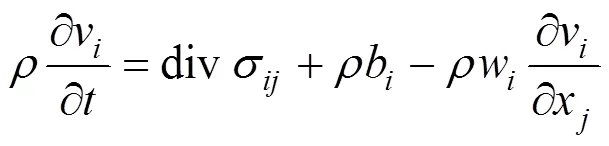
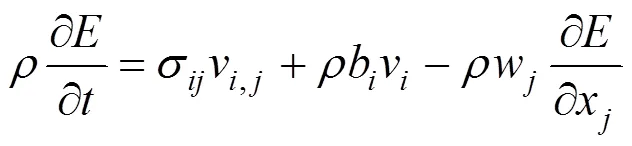
十字伞结构的控制方程[12]为:
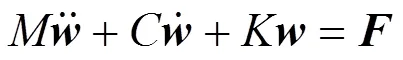
2 模型设置
2.1 背景介绍
文献[5]的垂直风洞试验在不严重影响十字伞稳定性的基础上,为了提高十字伞的滑翔能力,研究了5种伞衣面积相同而外形不同的十字伞,如图1所示。风洞试验中将A型伞设置为长宽比为3.0的基础伞型;B、C两种伞型针对十字伞的长宽比进行了调整,B型伞有着较大的长宽比,C型伞的长宽比较小;D、E型伞为异形结构,在长宽比为3.0的基础上提出对十字伞的形状进行修改,以期望获得较好的滑翔能力;其中D型伞采用的是文献[6]中首次提及到的杂交形状,E型伞采用非对称设置。对5种不同形状的十字伞在垂直风洞中相同的环境下进行了测试,试验比较分析了5种伞型在风洞试验中的稳定性,并通过控制器对十字伞伞绳进行操控使其具有一定的滑翔能力,然后通过传感器测得的数据来计算比较各个伞型的滑翔比。试验结果表明:与基础的伞型A相比,B型伞具有较好的稳定性,但滑翔能力较差;C型伞滑翔能力较强但稳定性较差;D型伞滑翔能力较强,但稳定性较差难以控制;E型伞的滑翔能力和稳定性能都较差。
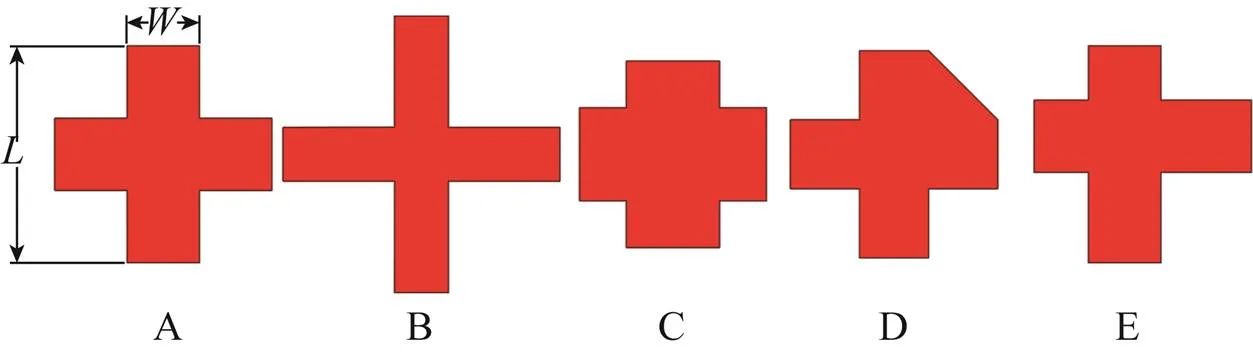
图1 不同伞型十字伞形状示意
2.2 计算模型和参数设置
本文将参照文献[5]中提及到的5种十字伞伞衣模型,通过仿真研究十字伞的充气性能和滑翔特性,其中充气性能主要通过充气后十字伞是否稳定和十字伞俯仰特性表现,而滑翔特性主要通过十字伞的滑翔比G来体现,滑翔比越高则滑翔性能越优秀。5种伞型的伞衣相关参数如表1所示。
表1 5种伞型的伞衣尺寸参数
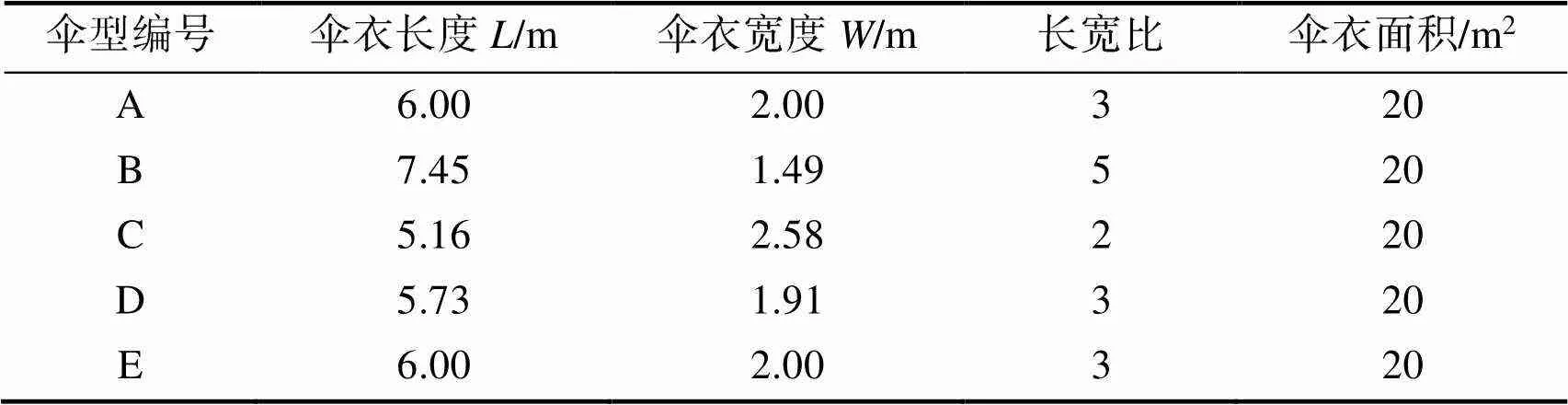
Tab.1 Dimensions of the five canopy types
为了简化计算,对十字伞模型作如下假设:1)伞衣为如图2所示的简单交叉结构,伞衣的每条伞辐上各有4条伞绳,4条伞绳通过连接绳与重物相连;2)模型只考虑伞绳的连接,对于伞衣径向带、顶孔绳等不作具体处理;3)伞衣采用壳单元,伞绳采用梁单元;4)重物为刚体,下表面通过连接绳与固定端相连,伞衣平面到重物的垂直距离为4m,重物通过一根连接绳与固定端相连,重物下表面与固定端的距离为1.6m。A型伞系统的几何模型,如图2所示。试验将通过5种伞型在展开过程中的表现及俯仰角来判断各种伞型的稳定性,试验中俯仰角即为十字伞中心点和重物中心点连线与竖直方向的夹角[3]。
在实际风洞试验中,重物端有两个执行器用于动态控制伞绳的长短。当试验中两个执行器控制的静态伞绳长度和动态伞绳长度均小于标称长度时,十字伞开始滑翔[4]。
为了比较各种十字伞型的滑翔特性,本文在充气稳定后的十字伞伞绳端施加一段时间的恒定载荷,用于模拟实际风洞实验中执行器对十字伞的控制作用,使十字伞具备一定的滑翔能力,具体操作为:通过关键字*DEFINE_CURVE来定义时间载荷曲线,按照定义的曲线,通过*LOAD_NODE将大小恒定的1kN载荷施加在其中的两根伞绳上,如图2中红色箭头所示。
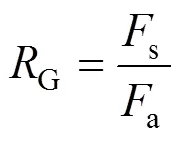
伞衣材料密度为74.00kg/m3,弹性模量为0.064GPa,泊松比为0.14,伞衣厚度为0.002 5m。伞绳材料密度为623.00kg/m3,弹性模量为10.90GPa,伞绳截面为圆形,圆截面的面积为7.068 6×10–6m2。
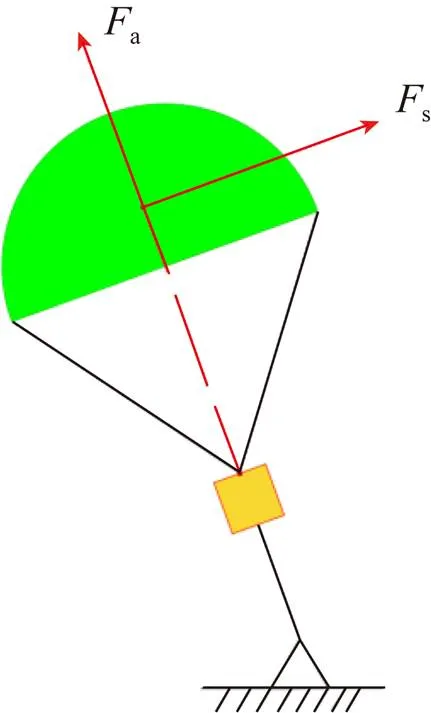
图3 侧向力和轴向力示意
3 关键字设置
LS-DYNA软件中S-ALE求解器的流场解算设置步骤为:1)通过ALE_STRUCTURED_CONTROL_POINTS关键字控制流场在三维方向上的位置和网格数量;2)通过ALE_ STRUCTURED_MESH创建网格;3)最后通过INITIAL_ VOLUME_FRACTION_GEOMETRY关键字对流场区域进行物质填充,对伞衣附近的流体域网格进行加密,加密区域网格尺度与伞衣表面网格尺度相同,加密区域以外至远场区域的网格逐渐稀疏,流场计算域网格划分如图4所示,流场入口处施加20m/s的恒定来流速度。

图4 流场计算域网格划分
除上述S-ALE特有的关键字外,其他的关键字设置[14-16]与ALE求解器相同,具体设置如表2所示。
表2 流固耦合过程关键字设置

Tab.2 Major keywords for fluid-structure interaction (FSI) setup
4 仿真结果及讨论
4.1 伞的充气性能分析
十字伞的充气性能主要通过充气稳定后的伞衣形状和俯仰特性来表现,这里选取伞衣变化幅度较大的几个时间节点(0.7s、1s、1.5s)记录图像,进行比较,并将整个试验过程划分为预充气阶段(0~0.7s)、充分充气阶段(0.7~1.5s)、充满后工作阶段(1.5~2.0s)第3个阶段来分析十字伞的充气性能,同时记录仿真结束时(2s时)十字伞伞衣和重物的相对位置,便于直观地比较十字伞的偏转情况,各伞型伞衣的具体状态如图6所示,对应的流固耦合现象如图7所示。俯仰特性主要通过最大俯仰角表现,通过仿真得到伞型A~E对应的最大俯仰角数据分别为0.86°、0.96°、10.7°、10.7°、16.0°。
结合图5~6可以清楚地看到十字伞充分展开的完整过程,这一过程大致可分为3个阶段:预充气状态、充分充气状态、充满气后工作阶段[17]。
1)预充气阶段(0~0.7s)。自流场入口处气流开始垂直上升,在充气后0.4s左右开始与伞衣接触,随着气流在伞衣部分的聚集,导致伞衣顶部逐渐形成高压区,并从伞顶逐渐扩散到伞衣底部,伞顶变化比较明显;当空气向十字伞顶部聚集时,伞衣和伞绳连接处因有束缚较少出现“卷边”现象;充气达0.7s时,十字伞初具雏形,此时5种伞型都呈较为稳定状态。

图5 不同伞型伞衣变化
2)充分充气阶段(0.7~1.5s)。从开始充气后的0.7s到1.0s,伞衣的变化幅度最为剧烈,由于气流对十字伞的持续作用,伞衣继续膨胀,到达1.0s左右时,伞衣变形达到最大,随后,聚集在伞顶端的气流向四周流动,内部气流速度逐渐变小并绕伞衣底边处流出,伞臂逐渐向外张开,且降落伞开始旋转和摆动;到达1.5s时,伞衣形状经过多次调整后趋于稳定,基本不再发生大幅度的变化。在这一阶段可以明显观察到五种伞型的变化趋势略有不同,根据图6中5种伞型的速度分布云图可以看出:A、B型伞的稳定性较强,C型伞在气流通过后伞衣变化较为剧烈,D、E型伞由于非对称性的影响,气流通过时,伞衣表现出了更为严重的失稳现象。

图6 不同形状十字伞的流固耦合现象
3)充满后工作阶段(1.5~2.0s)。这个阶段的十字伞伞衣形状变化幅度较小,表现出有规律的“呼吸”现象。原先在伞顶上方的对称涡旋变得极为不稳定,在不对称的涡旋和压差的作用下,伞衣开始向其他方向摆动,摆动的位置也会在相应部位产生非对称涡旋,但大小和发展趋势不确定,伞因此产生绕固定端打转、前后左右随机摆动等现象[16],十字伞的偏转主要发生在这个阶段。因此,此阶段5种伞型的区别最为明显。观察图5~6中充气2s时各伞型的位置和速度分布云图,可以明显看出,A、B型伞偏转较小,C、D、E型伞偏转较大。
综合上述分析以及最大俯仰角数据,可以得出:A、B型伞最大俯仰角较小,有较强的稳定性,充气性能较好;C、D、E型伞的最大俯仰角较大,稳定性较差,充气性能较差。数值模拟结果与文献[5]中垂直风洞试验得到的结论一致。
4.2 伞的滑翔特性分析
通过LS-DYNA对有无施加载荷得到的受力情况进行比较分析,5种伞型施加载荷前后的轴向力与侧向力如图7所示。记录仿真结束时各个伞型的形状如图8所示。
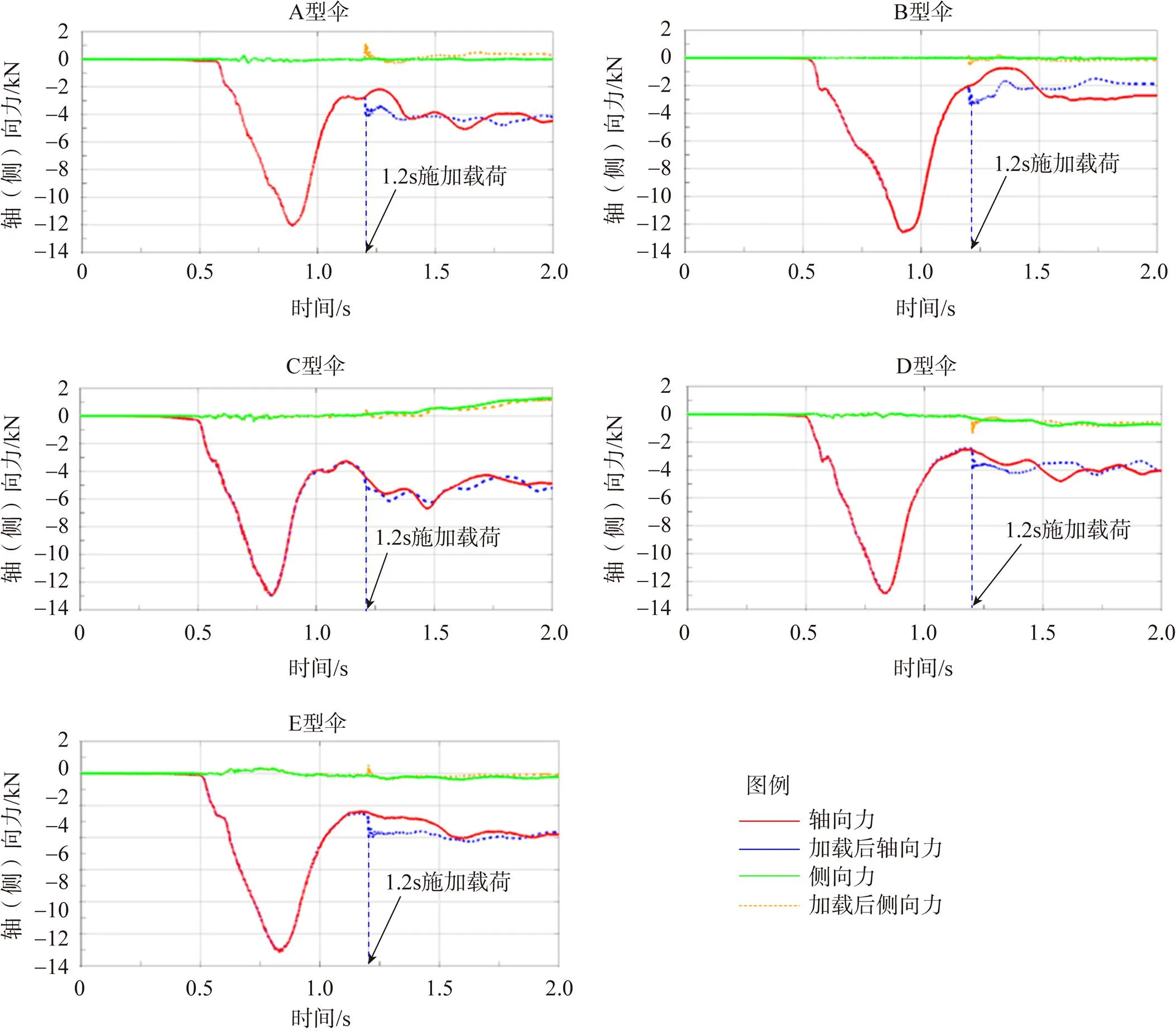
图7 不同形状十字伞受力曲线(1.2s施加载荷)

图8 2s时不同伞型受力后形状变化(从左到右依次为A、B、C、D、E型)
结合图7~8进行分析发现,A型伞在施加控制之后,侧向力提升较为明显,且相较未施加载荷(图5)有明显的滑翔能力;B型伞和E型伞即使在施加控制之后侧向力也无明显提升,滑翔能力较差。而C、D型伞在施加控制之前就已经有较大的侧向力,滑翔能力相较于其他伞型较强。
从图7曲线中提取3组数据计算施加控制后5种十字伞的滑翔比,结果如表3所示:
表3 5种十字伞不同时刻的滑翔比
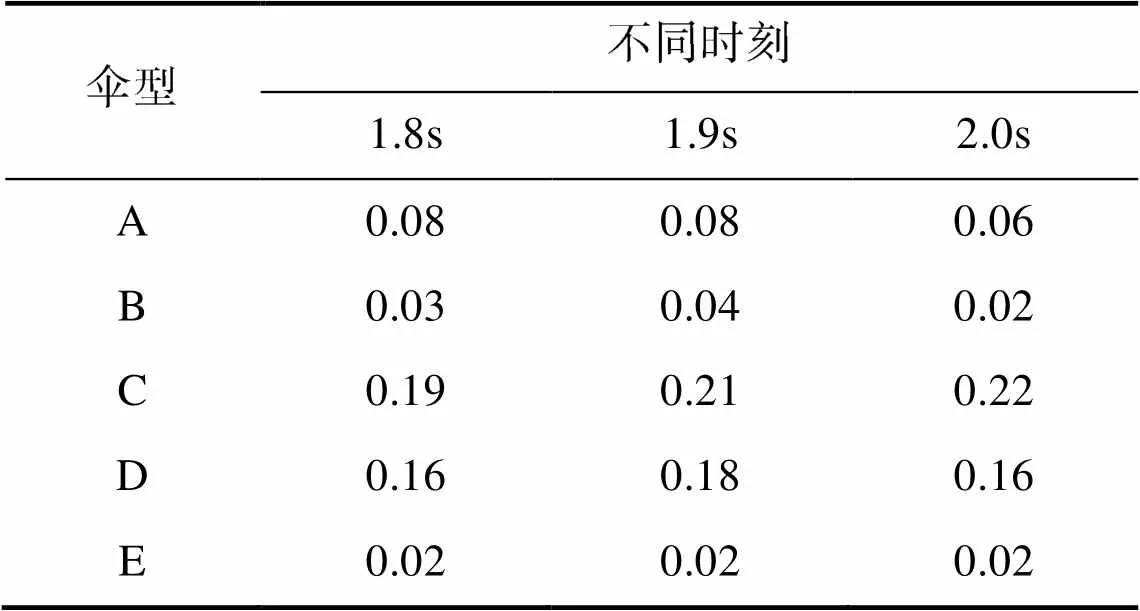
Tab.3 Glide ratios of cruciform parachutes at different time steps
综上,滑翔能力的数值模拟结果表明:与基准的A型伞相比,C、D型伞的滑翔能力有显著提高,B、E型伞的滑翔能力较差,即使在施加载荷后也无明显提升,该项模拟结果与文献[5]中的垂直风洞试验结论一致。
5 结束语
本文利用LS-DYNA中的S-ALE求解器对5种不同伞衣形状的十字伞进行了数值模拟,分析比较几何外形对十字伞充气和滑翔性能的影响,数值模拟结果显示,不同几何形状的十字伞充气展开后的充气性能和滑翔特性有着较大的差异,具体表现为:
1)十字伞的长宽比A会影响到俯仰特性和稳定性,对滑翔能力的影响较大:与A型基准伞相比,A较大的伞(B型伞)展开后的俯仰特性和稳定性较好,而A较小的伞(C型伞)俯仰特性和稳定性较差。A较小的伞的滑翔能力较强,而A较大的伞滑翔能力表现较差。
2)异形结构会严重影响十字伞的俯仰特性和稳定性,但对滑翔能力的影响因伞型不同而有所区别,其中D型伞相较于A型基准伞而言,俯仰特性和稳定性较差,但滑翔能力有一定的提升;而非对称结构的E型伞在数值模拟中既没有很好的稳定性和俯仰特性,也无法在施加载荷控制后使滑翔能力得到显著提升。
3)通过在十字伞的伞绳端施加恒定载荷的方式来模拟垂直风洞试验中对伞绳的控制效果,由于风洞试验中未明确施加载荷的大小,且载荷大小可能随着时间而变化,因此无法定量比较风洞试验和数值模拟得到的滑翔比结果,后续将分析降落伞在重物上的吊点分布、重物的几何尺寸、质量、惯量,固定端与重物的连接等因素对结果产生的影响,更加准确地模拟风洞试验中的控制效果,得到更为精确的结果。
[1] CIVELEK B, KIVRAK S. A Review on the Precision Guided Airdrop Systems[J]. International Journal of Latest Technology in Engineering, Management & Applied Science, 2019, 8(1): 15-17.
[2] FAGLEV C P, SEIDEL J, MCLAUGHLIN T E, et al. Computational Study of Air Drop Control Mechanisms for Cruciform Parachutes[C]//24th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar 2017, June 5-9, 2017, Denver, Colorado, USA. Reston, VA: AIAA, 2017: 5-9.
[3] NOETSCHER G, ROSE T M, BERGERON K. Modeling and Experimental Efforts towards Robust Low-Cost Cruciform Canopy Control[C]//Aerodynamic Decelerator Systems Technology: AIAA Aviation Forum 2019, June 17-21, 2019, Dallas, Texas, USA. Reston, VA: AIAA, 2019.
[4] HERRINGTON S M, RENZELMAN J T, FIELDS T D, et al.Vertical Wind-Tunnel Testing of Steerable Cruciform Parachute System[J].Journal of Aircraft, 2018, 56(2):747-757.
[5] HERRINGTON S M, RENZELMAN J T, FIELDS T D, et al. Experimental Investigation into the Effects of Geometry on the Glide Performance of Cruciform Parachutes[C]//Aerodynamic Decelerator Systems Technology: AIAA Aviation Forum 2019, June 17-21, 2019, Dallas, Texas, USA. Reston, VA: AIAA, 2019.
[6] JEAN P, JASON P, ERIC B, et al. Glide Performance Study of Standard and Hybrid Cruciform Parachutes[C]//17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, May 19-22, 2003, Monterey, California. [S.l.]: AIAA,2003.
[7] GAO Xinglong, ZHANG Qingbin, CHEN Qin, et al. Fluid-structure Interactions on Steerable Cruciform Parachute Inflation Dynamics[C]//5th International Conference on Mechanical and Aeronautical Engineering: ICMAE 2019, Sanya, China, December 12-15, 2019. Bristol, UK: Institute of Physics, 2020.
[8] 连红博, 喻东明, 周昊, 等. 十字型阻力伞充气过程的数值模拟[J]. 航空兵器, 2021, 28(6): 83-87.
LIAN Hongbo, YU Dongming, ZHOU Hao, et al. Numerical Simulation on Inflation Process of Cruciform Drag Parachute[J]. Aero Weaponry, 2021, 28(6): 83-87. (in Chinese)
[9] 杨品, 胡雪鹏, 金楼. 基于LS-DYNA的某型阻力伞半折叠数值仿真研究[C]//第八届中国航空学会青年科技论坛, 2018年11月4-6日, 江门. 2018: 774-781.
YANG Pin, HU Xuepeng, JIN Lou. Numerical Simulation Study of a Certain Drag Parachute Based on LS-DYNA[C]//The 8th Youth Forum of Chinese Society of Aeronautics, November 4-6, 2018, Jiangmen. 2018: 774-781. (in Chinese)
[10] 房明. 火箭橇-阻力伞系统力学特性与流场分析[D].南京: 南京航空航天大学, 2018.
FANG Ming. Dynamic Characteristics and Flow Field Analyses on a Rocket Sled-Drag Parachute System[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2018. (in Chinese)
[11] 李裕春, 时党勇, 赵远. ANSYS11.0/LS-DYNA基础理论与工程实践[M]. 北京: 中国水利水电出版社, 2008.
LI Yuchun, SHI Dangyong, ZHAO Yuan. ANSYS11.0/LS-DYNA Foundation Theory and Engineering Practice[M]. Beijing: China Water & Power Press, 2008. (in Chinese)
[12] 徐琳, 梁建, 段丽华, 等. 基于CSD/CFD舵面气动力流固耦合仿真分析[J]. 航空兵器, 2020, 27(2): 47-52.
XU Lin, LIANG Jian, DUAN Lihua, et al. Fluid Solid Coupling Simulation Analysis of Rudder Surface Aerodynamic Based on CSD/CFD[J]. Aero Weaponry, 2020, 27(2): 47-52. (in Chinese)
[13] JORGENSEN D S. Cruciform Parachute Aerodynamics[D]. Leicester: University of Leicester, 1982.
[14] 王中阳. 降落伞充气过程动力学数值模拟[D]. 南京: 南京航空航天大学, 2013.
WANG Zhongyang. The Dynamic Numerical Simulation of the Parachute Inflation[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013. (in Chinese)
[15] 贾贺, 荣伟, 陈国良. 基于LS-DYNA的降落伞伞衣织物透气性参数仿真验证[J]. 航天返回与遥感, 2009, 30(1): 15-20.
JIA He, RONG Wei, CHEN Guoliang. The Use of LS-DYNA to Simulate the Permeability Parameters of the Parachute Canopy[J]. Spacecraft Recovery & Remote Sensing, 2009, 30(1): 15-20. (in Chinese)
[16] 贾贺, 荣伟, 陈国良. 基于LS-DYNA软件的降落伞充气过程仿真研究[J]. 航天器环境工程, 2010, 27(3): 367-373.
JIA He, RONG Wei, CHEN Guoliang. The Simulation of Parachute Inflation Process Based on LS-DYNA Software[J]. Spacecraft Environment Engineering, 2010, 27(3): 367-373. (in Chinese)
[17] 程涵, 余莉, 李胜全. 基于ALE的降落伞充气过程数值仿真[J]. 南京航空航天大学学报, 2012, 44(3): 290-293.
CHENG Han, YU Li, LI Shengquan. Numerical Simulation of Parachute Inflation Process Based on ALE[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(3): 290-293. (in Chinese)
Effects of Geometry on the Inflation and Gliding Performance of Cruciform Parachutes
HUANG Yunyao1,3WU Shiqing2,3ZHANG Yang1,3,*
(1 College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)(2 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)(3 Laboratory of Aerospace Entry, Descent and Landing Technology, CASC, Beijing 100094, China)
In order to study the effect of geometry on the inflation and glide performance of cruciform parachute, the S-ALE (Structured Arbitrary Lagrange-Euler) fluid-structure interaction solver in LS-DYNA is employed. Cruciform parachutes with five different canopy shapes are taken and the corresponding dynamic opening process are simulated. The inflated shapes of the cruciform parachutes at different time instants are obtained and the inflation performances are compared. Furthermore, loads are applied to these stably inflated cruciform parachutes to test and compare the glide performance. Numerical results show that the abnormal structure has a great influence on the inflation performance but varies with the type of the parachute on the glide performance, whereas the aspect ratio impacts a lot on both of the inflation and glide performance.
inflation performance; glide performance; cruciform parachutes; fluid-structure interaction; spacecraft recovery
O35
A
1009-8518(2022)05-0048-11
10.3969/j.issn.1009-8518.2022.05.005
2022-07-05
航天进入减速与着陆技术实验室开发基金(EDL19092128)
黄云尧, 武士轻, 张扬. 几何形状对十字伞充气和滑翔性能的影响[J]. 航天返回与遥感, 2022, 43(5): 48-58.
HUANG Yunyao, WU Shiqing, ZHANG Yang. Effects of Geometry on the Inflation and Gliding Performance of Cruciform Parachutes[J]. Spacecraft Recovery & Remote Sensing, 2022, 43(5): 48-58. (in Chinese)
黄云尧,男,1997年生,南京航空航天大学机械专业在读硕士研究生,主要研究方向为流固耦合、航天器返回技术。E-mail:huangyy1415@qq.com。
武士轻,男,1982年生,2008年获长春理工大学机械电子工程专业硕士学位,高级工程师。主要研究方向为航天器无损着陆技术。E-mail:wushi508@foxmail.con。
张扬,男,1987年生,2016年获南京航空航天大学流体力学专业博士学位,副研究员。主要研究方向为流固耦合、航天器返回技术。E-mail:zhy@nuaa.edu.cn。
(编辑:夏淑密)

