钢筋与FRP筋混杂配筋混凝土梁的抗弯性能

张智梅,魏久

(上海大学土木工程系,上海 200444)

腐蚀环境中的混凝土构件常面临因钢筋锈蚀而导致的结构构件耐久性和承载力下降的问题[1],而纤维增强复合材料(fibre reinforced plastic,FRP)具有轻质、高强、耐腐蚀性能好等优点[2],因此,以FRP筋取代钢筋可有效解决钢筋锈蚀带来的不利影响.但由于FRP筋弹性模量较低且为线弹性材料,FRP筋混凝土受弯构件在使用时易产生过大的挠度和裂缝宽度,甚至发生脆性断裂[3],这又使得FRP筋混凝土梁的应用受到一定限制.

近年来许多学者提出了混杂配筋梁的概念,即仅用FRP筋代替混凝土梁中部分处于边角、易发生锈蚀部位的钢筋,而其余部位钢筋保持不变.混杂配筋梁既能发挥钢筋的延性性能,又能发挥FRP筋的耐腐蚀性能[5].在试验研究方面,Ombres等[5]发现在纯芳纶纤维增强复合材料(aramid-FRP,AFRP)筋梁中增加钢筋,随着钢筋含量增多,构件的延性、刚度较好,裂缝宽度减小.Lau等[6]提出了混杂FRP筋梁等效配筋率的概念,发现混杂BFRP筋梁的极限荷载、延性均随等效配筋率的增大而增大.孔祥清等[7]通过试验研究了不同荷载等级作用下混杂玄武岩纤维增强复合材料(basalt-FRP,BFRP)筋梁的混凝土应变沿截面高度的变化,发现混杂FRP筋梁受弯过程中仍满足平截面假定.We等[8]制作了3根混杂BFRP筋混凝土梁,发现梁挠度随筋面积与钢筋面积之比的增大而增大,而刚度则相反.在理论研究方面,葛文杰等[9]指出混杂FRP筋梁存在适筋、少筋和超筋3种破坏模式,并给出相应的判别条件.张晓亮[10]、Qu等[11]和黄海群[12]推导了混杂FRP筋梁抗弯承载力计算公式.Kara等[13]考虑受拉区混凝土作用依据混凝土梁抗弯设计方法,推导出了混杂FRP筋梁抗弯承载力公式.综上所述,目前对混杂FRP筋梁开展的一系列研究主要以试验为主,但现有理论尚不足以建立针对混杂FRP筋梁抗弯设计的相应规范.另外,在试验研究基础上借助有限元方法可以分析混杂FRP筋梁抗弯承载力的主要影响因素,并据此深化混杂FRP筋梁的抗弯理论.

因此,本工作首先运用有限元软件ABAQUS对已有混杂FRP筋试验梁进行建模和分析,并对影响混杂FRP筋梁抗弯性能的主要因素进行参数分析;然后,基于有限元分析结果建立适筋破坏时的FRP筋应力表达式和混杂FRP筋梁抗弯承载力计算公式;最后,利用已有试验数据验证FRP筋应力表达式的准确性.

1 有限元模型

1.1 试验

本工作基于文献[11]中的试验梁进行有限元模拟,梁尺寸、FRP筋及钢筋的布置如图1所示.试验时采取4点对称加载方式,其中P/2表示竖向外加荷载.试验共有8根梁,其中B1为钢筋混凝土梁,B2为玻璃纤维增强复合材料(glass-FRP,GFRP)筋混凝土梁,B3～B8为钢筋和GFRP筋混杂配筋梁.试验主要研究等效配筋率对混杂GFRP筋梁极限荷载的影响,其中B1～B8的等效配筋率分别为1.14%、0.29%、0.71%、0.71%、1.08%、1.16%、0.35%、3.49%.表1为试验中材料的力学性能.

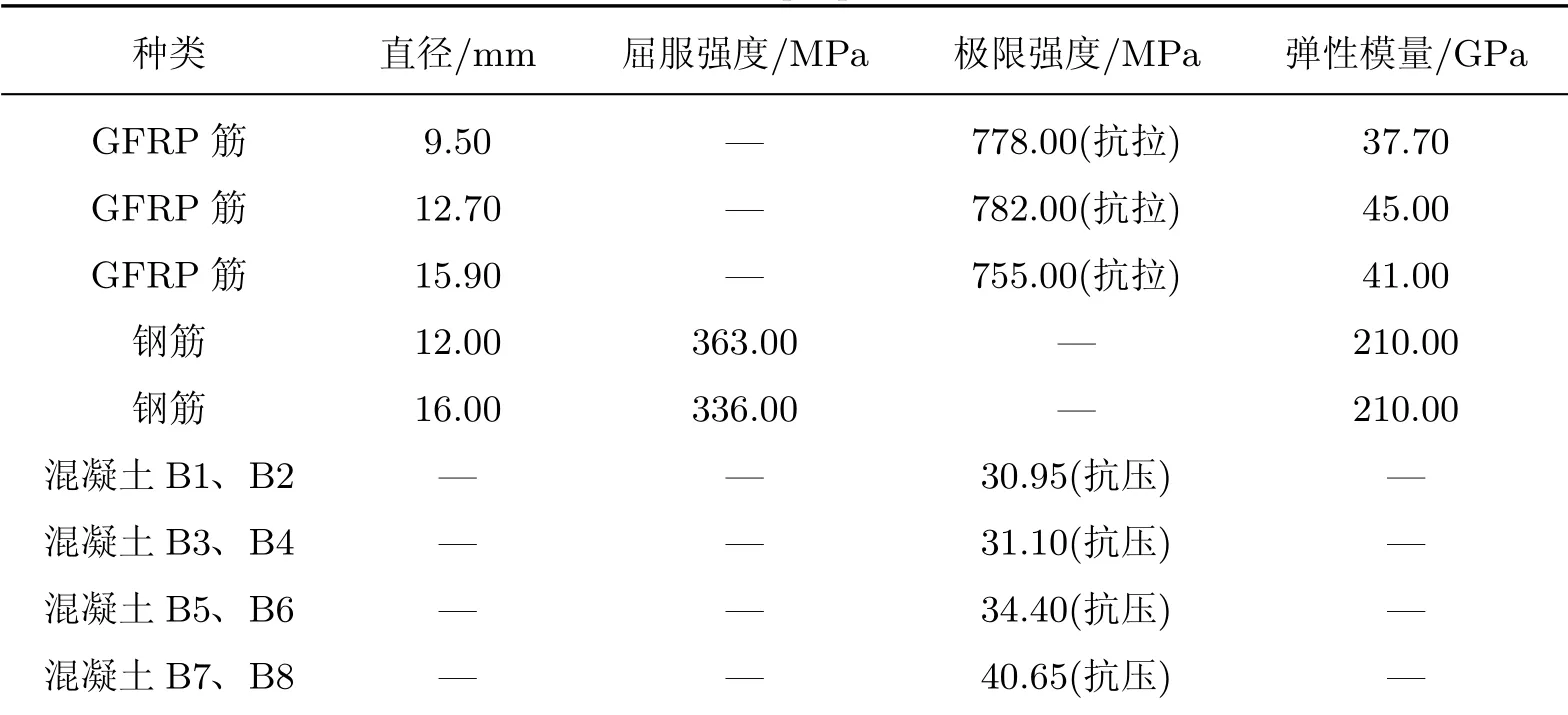
表1 材料力学性能Table 1 Mechanical properties of materials

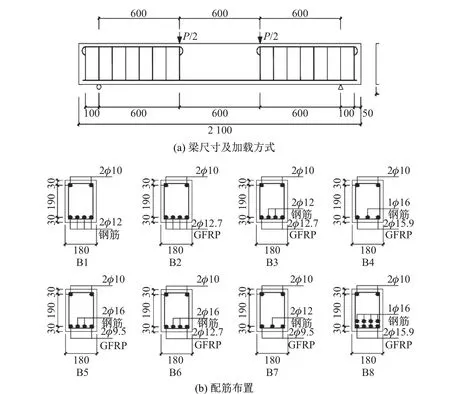
图1 梁尺寸及配筋示意图(单位:mm)Fig.1 Schematic diagram of beam dimensions and reinforcement(Unit:mm)

1.2 有限元模型的建立

本工作应用有限元软件ABAQUS对试验梁进行三维建模.为了避免应力集中导致分析难以收敛,建模时在支座处及加载点处分别放置了刚性垫块.混凝土、垫块采用三维实体单元,单元类型为C3D8R;钢筋、FRP筋采用桁架单元,单元类型为T3D2.混凝土采用ABAQUS软件中的塑性损伤模型,其单轴受拉和单轴受压应力-应变曲线采用《GB50010-2010混凝土结构设计规范》(以下简称规范)中相应的受拉和受压本构;垫块采用线弹性材料,其本构按钢材设置;钢筋本构采用规范中双线性弹塑性模型;FRP筋本构采用线弹性模型.

假设钢筋、FRP筋与混凝土之间未发生黏结滑移,采用内置区域约束,垫块与混凝土采用绑定约束,加载点与垫块采用耦合约束.边界条件按简支梁设置,即一端U1=U2=U3=UR1=UR2=0,另一端U2=U3=UR1=UR2=0.为了保证精度及收敛性,本工作采用位移加载方式.图2为划分网格后的有限元模型.

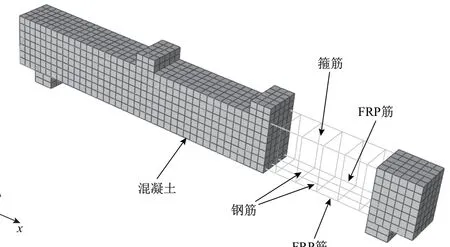
图2 有限元模型Fig.2 Finite element model

1.3 有限元模型有效性验证

对各试验梁建模并进行非线性有限元分析,限于篇幅,仅给出部分试验梁的荷载-跨中位移曲线.图3为B1～B4试验梁的荷载-跨中位移曲线.由图可见,B1～B4的数值模拟曲线与试验曲线吻合较好.另外,B3和B4混杂配筋梁的荷载-跨中位移曲线呈现明显的三阶段特征:混凝土梁开裂前的弹性阶段,混凝土梁开裂后到钢筋屈服时的弹塑性阶段,以及钢筋屈服后到梁破坏时的塑性阶段.

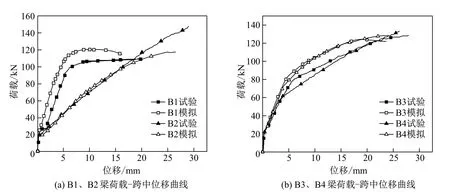
图3 数值模拟结果与试验结果的对比Fig.3 Comparison between numerical simulation and experimental results

为了进一步分析模型的正确性,表2给出了试验梁极限荷载和破坏模式的数值分析与试验结果的对比.由表2可见:极限荷载的模拟值与试验值较为吻合;数值分析与试验结果的破坏模式均相同.模拟值与试验值之比的均值、标准差和变异系数分别为0.97、12.60%和12.9%,二者存在一定差别的主要原因可能是模拟时所用混凝土本构与材料实际性能并不完全相符.综上表明,本工作建立的有限元分析模型是正确的,可用于后续影响因素的分析.

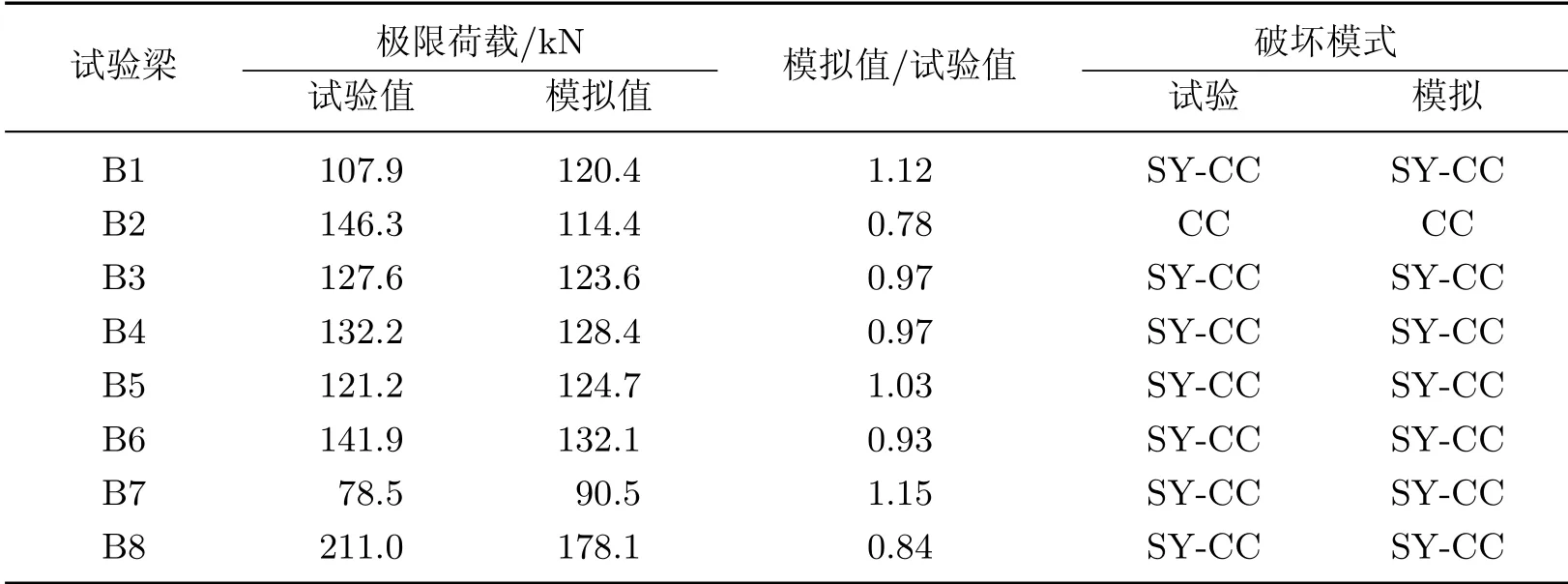
表2 试验梁极限荷载和破坏模式的数值分析与试验结果的对比Table 2 Numerical analysis and test results comparison of ultimate load and failure modes of each beam

2 影响因素分析

Mustafa等[3]发现,GFRP/钢筋混杂配筋梁在混凝土开裂和钢筋屈服后,梁的刚度明显降低,挠度明显增大,而混凝土开裂后的刚度和变形性能则优于前者.Qu等[11]认为等效配筋率是预测混杂GFRP筋梁抗弯承载力时的一个重要指标,而双层或单层配筋方式对其极限荷载的影响不大.由此可见,除了混凝土强度外,FRP筋种类、等效配筋率是影响混杂FRP筋梁抗弯性能的主要因素.因此,本工作模拟分析FRP筋种类、混凝土强度和等效配筋率对混杂FRP筋梁抗弯性能的影响.模拟方案见表3,其梁编号B3-X-Y-Z的含义:B3表示以试验梁B3为建模基准梁,X代表混凝土强度,Y代表FRP筋的种类,Z代表等效配筋率.FRP筋材料性能参数见表4.各单一变量分析的结果见图4.

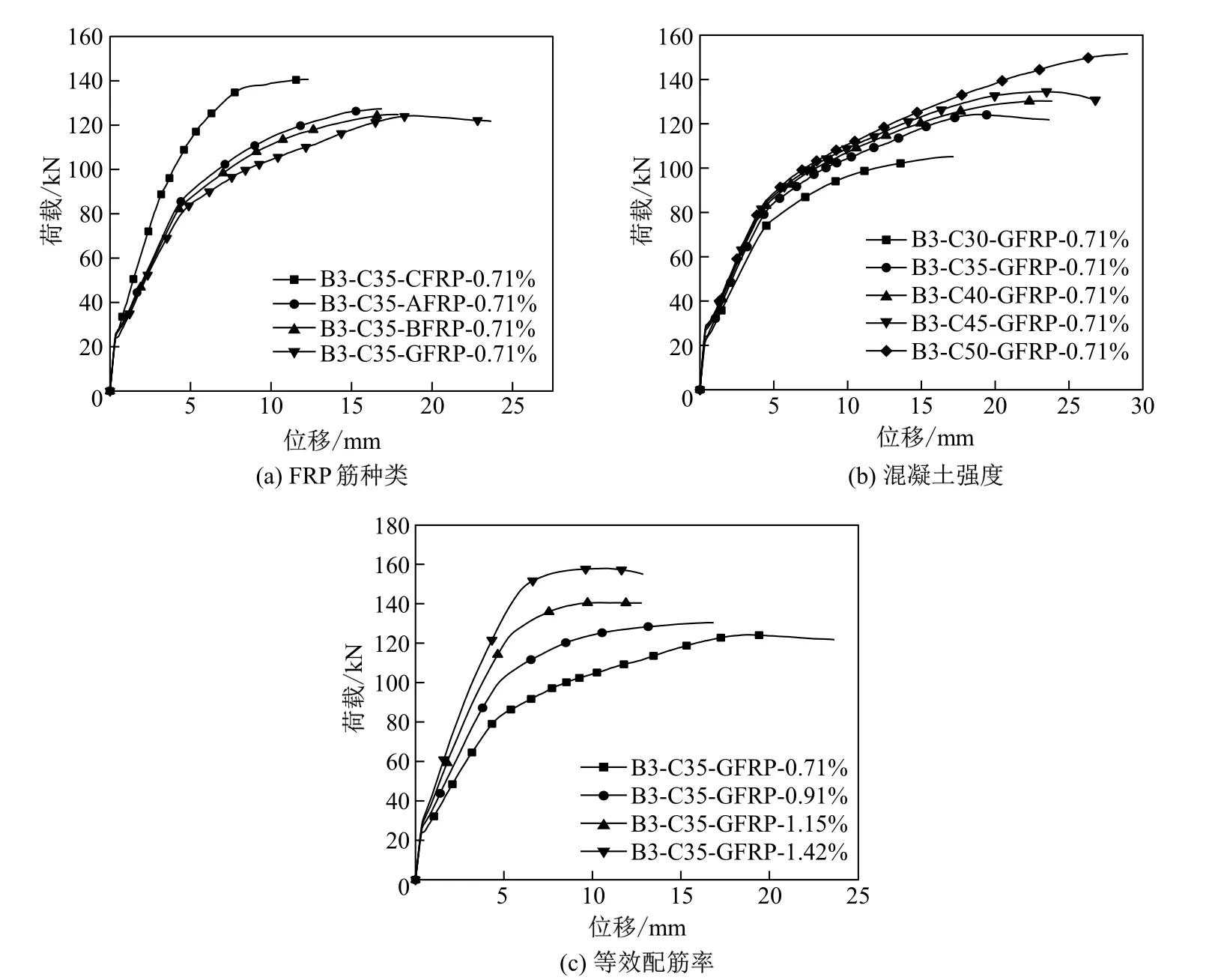
图4 3种因素影响下的荷载-跨中位移曲线Fig.4 Load-mid-span displacement curve under 3 kinds of factors

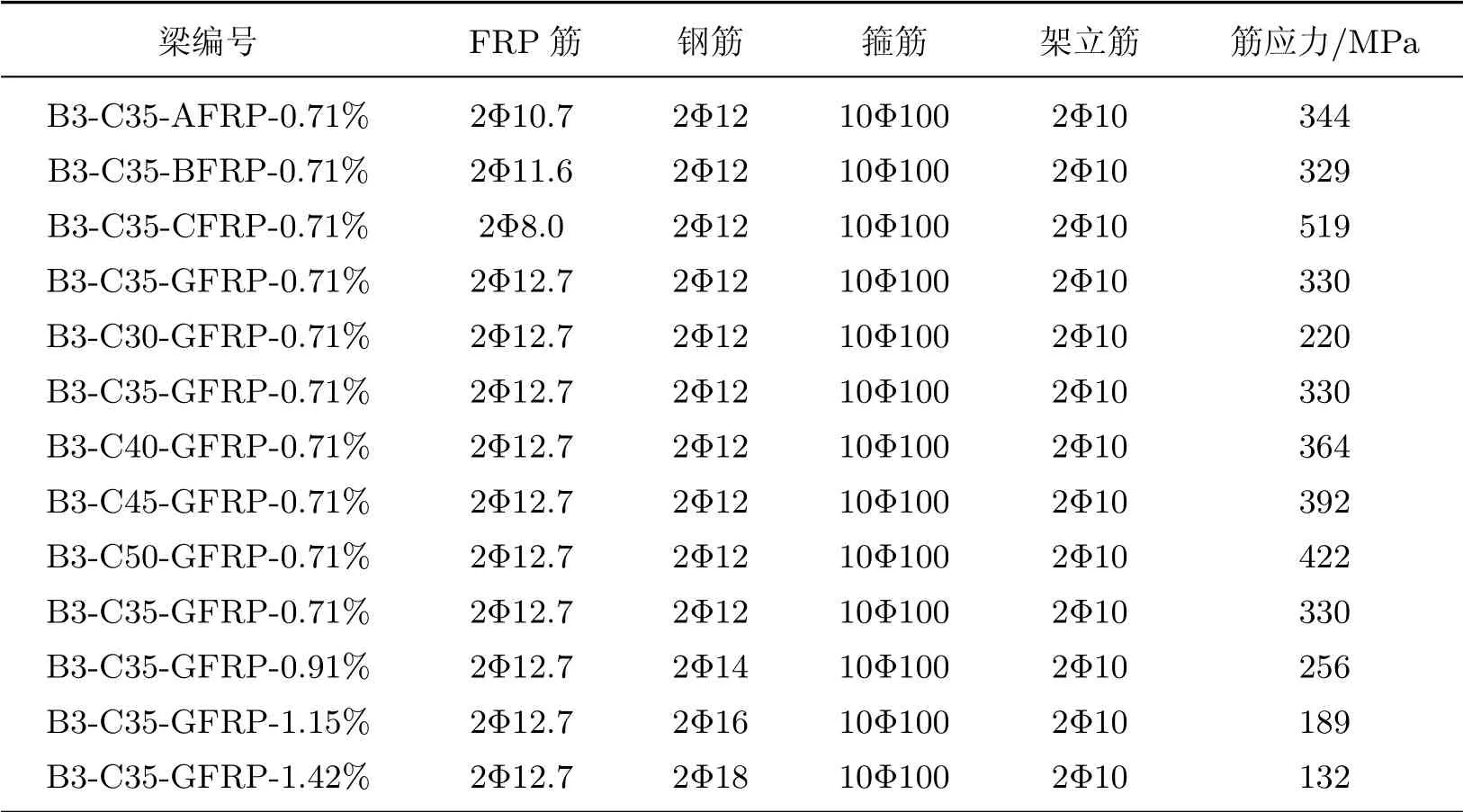
表3 数值模拟方案和FRP筋应力数值计算结果Table 3 Numerical simulation scheme and numerical calculation results of FRP bar stress

2.1 FRP筋种类

由图4(a)可知:无论FRP筋种类如何,混杂配筋梁都呈现出较为明显的弹性、弹塑性和塑性三阶段变形特性;混杂CFRP筋梁破坏时极限荷载最大、挠度最小,其余3种混杂FRP筋梁破坏时极限荷载差别不大且均小于混杂CFRP筋梁,但挠度均比混杂CFRP筋梁大,其中混杂GFRP筋梁的挠度最大.以上分析表明:FRP筋种类(弹性模量)对梁抗弯性能影响较大;在混凝土强度、等效配筋率相同的情况下,通过改变FRP筋种类难以兼顾承载能力和延性性能.

2.2 混凝土强度

由图4(b)可见:混凝土强度对混杂GFRP梁在弹性和弹塑性阶段刚度的影响不大;但随着混凝土强度的提高,混杂GFRP筋梁在塑性破坏阶段的刚度、挠度和极限荷载均逐渐增大.因此,建议在设计混杂FRP筋梁时可以选用强度等级较高的混凝土.

2.3 等效配筋率

由图4(c)可见:在弹性阶段,等效配筋率对梁刚度的影响不大;在弹塑性阶段,随等效配筋率增加,梁的刚度不断增大;进入塑性破坏阶段后,梁刚度却随等效配筋率的增大而有所减小,挠度也相应减小.另外,等效配筋率从0.71%提升到1.42%时,混杂GFRP筋梁极限荷载由127.6 kN提高到158.0 kN,提高了约24%,说明等效配筋率对混杂FRP筋梁的承载力影响较大.

综上分析可知:等效配筋率对混杂FRP筋梁的承载能力和变形性能影响最为显著,其次为FRP筋种类,而混凝土强度对承载力有一定的影响,但对刚度影响较为有限.

3 抗弯承载力分析

3.1 等效配筋率与平衡配筋率

分析混杂FRP筋梁的抗弯性能需要考虑等效配筋率和平衡配筋率.等效配筋率ρeff是将钢筋和FRP筋按照刚度等效的原则来计算,有

式中:Es和Ef分别为钢筋和FRP筋弹性模量;As和Af分别为钢筋和FRP筋面积;b为梁的宽度;h0为梁截面的有效高度;ρs和ρf分别为钢筋和FRP筋的配筋率.

混杂FRP筋梁的平衡配筋率ρeffb可分为两种情况定义:钢筋屈服与混凝土压碎同时发生时的配筋率ρeffb1;FRP筋拉断与混凝土压碎同时发生时的配筋率ρeffb2.根据构件的变形协调方程和平衡方程可推得

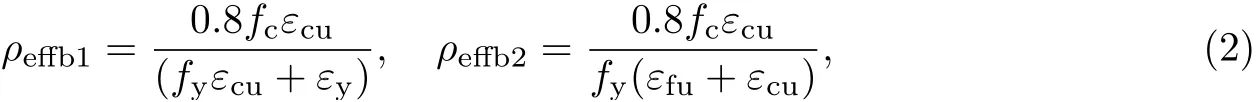
式中:εcu为混凝土极限压应变;εy为钢筋屈服应变;εfu为FRP筋极限拉应变;fy为钢筋屈服强度;fc为混凝土轴心抗压强度.

依据文献[9]和[11],当ρeff＜ρeffb2时,混杂FRP筋梁将发生脆性破坏;当ρeff＞ρeffb1时,混杂FRP筋梁将发生超筋破坏;当ρeffb2＜ρeff＜ρeffb1时,混杂FRP筋梁发生适筋破坏,破坏时梁表现出较好的延性性能,也是设计时希望发生的破坏模式.因此,本工作中以下有关承载力的分析均是针对适筋破坏梁.

3.2 抗弯承载力

本工作推导的公式是建立在以下假设条件:①混杂FRP筋梁符合平截面变形假定;②钢筋和FRP筋与混凝土之间均不发生无黏结滑移;③不考虑受拉区混凝土的作用.根据平衡条件,发生适筋破坏时混杂FRP筋梁正截面的抗弯承载力为

式中:ff为FRP筋应力;β为混凝土受压区高度等效系数,可按规范中的规定取值;混凝土受压区高度x可由式(4)求得.

式(3)中计算FRP筋的应力ff是关键.由式(4)及基于平截面假定的变形协调方程可推得

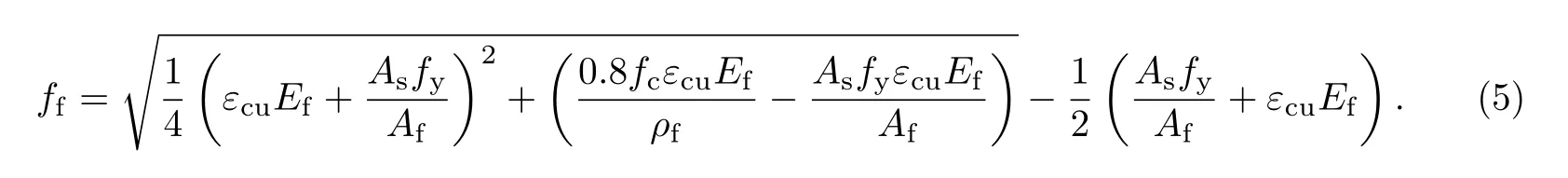
为了便于实际工程应用,对式(5)进行简化.

(1)假设FRP筋应力ff与FRP筋种类(弹性模量Ef)的关系为

根据表3中的筋应力值,将其与FRP筋的弹性模量进行拟合(见图5(a)),可得

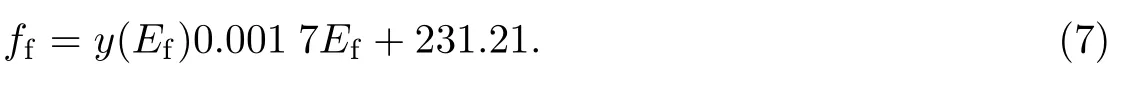
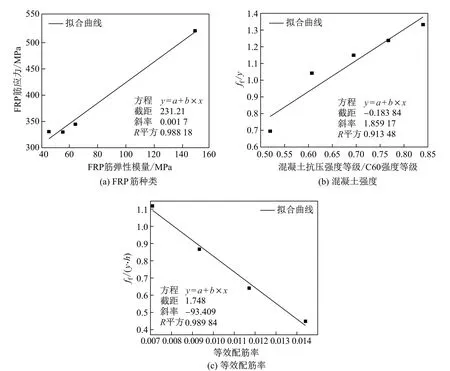
图5 FRP筋应力与3种影响因素的关系Fig.5 The relationship between the stress of FRP bars and elastic modulus of FRP bars

(2)在式(6)的基础上进一步建立ff与混凝土强度fc的关系.为了使左右量纲相等,引入C60对应的混凝土抗压强度fc60,假设二者之间的关系为

根据表3中的筋应力值,将其与混凝土强度进行拟合(见图5(b)),可得

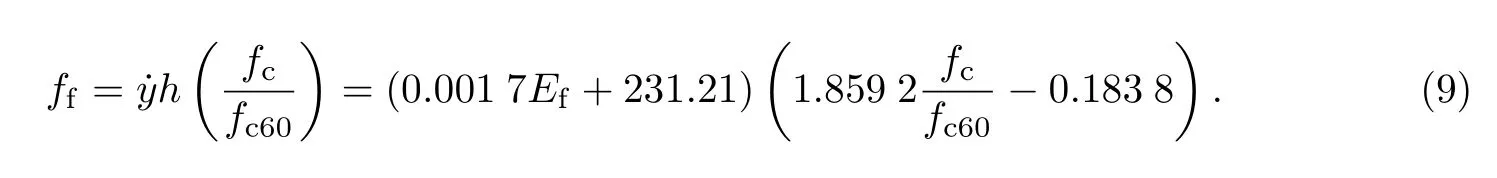
(3)基于式(7),假设ff与等效配筋率的关系为

根据表3中的筋应力值,将其与等效配筋率进行拟合(见图5(c)),可得

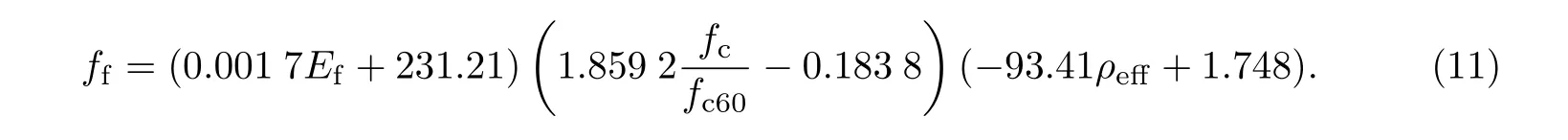
综上所述,适筋破坏时混杂FRP筋梁正截面抗弯承载力可按照式(5)计算,其中x和ff分别由式(4)和(8)计算.

4 正确性验证

为了检验本工作建立的混杂FRP筋梁中FRP筋应力计算公式(12)的准确性,本工作收集了国内外学者所做的25根混杂FRP筋试验梁的数据,将各梁根据试验数据计算得到的抗弯承载力试验值与按本工作计算得到抗弯承载力计算值进行对比,结果见表5.剔除打星号的不符合适筋梁的数据后,经统计可知弯矩计算值与试验值之比的均值、标准差和变异系数分别为1.0、0.1和0.1.由此可见,利用式(3)、(4)和(8)计算混杂FRP筋梁抗弯承载力较为准确,侧面说明式(8)也是准确的.

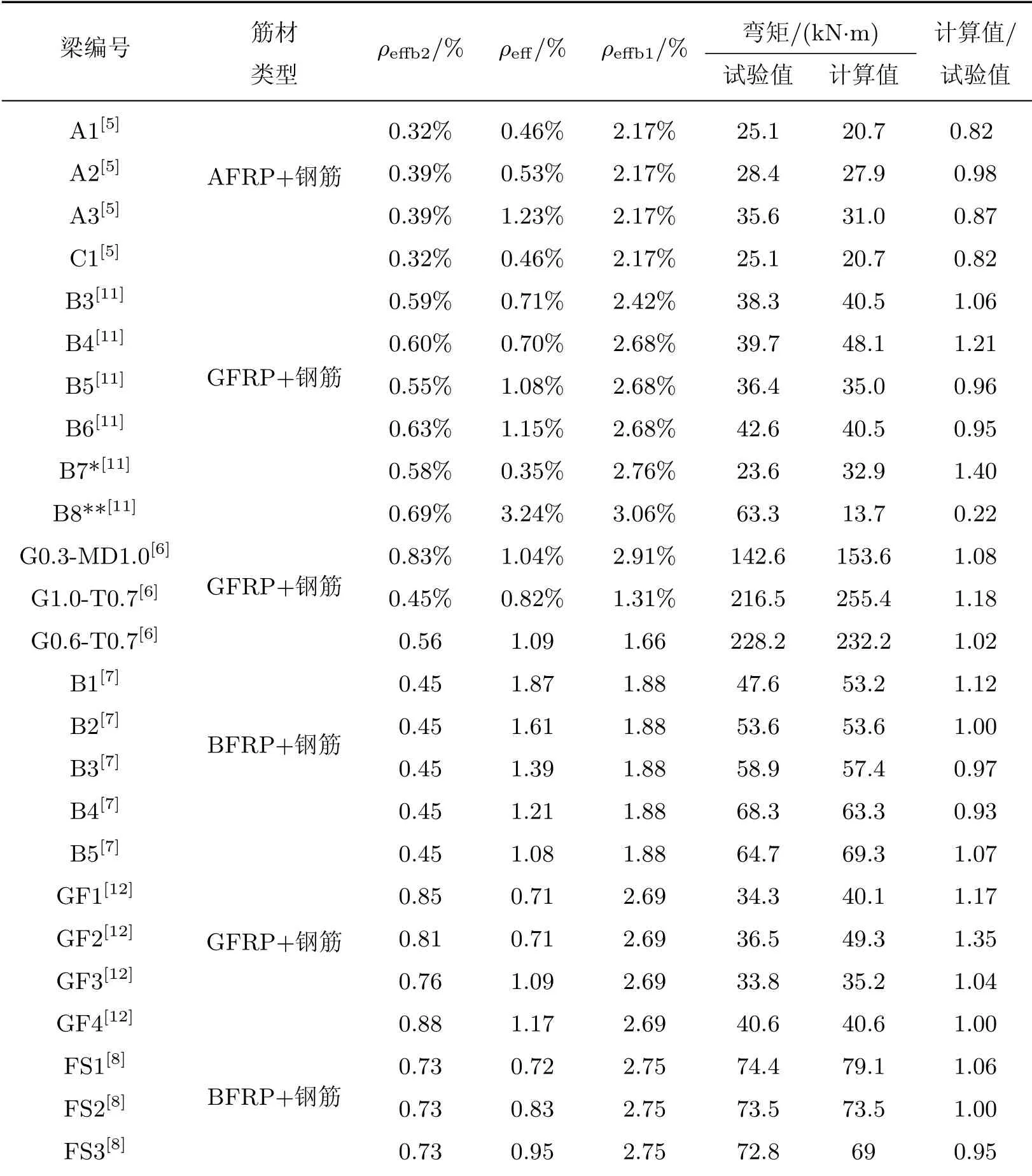
表5 混杂FRP筋梁弯矩计算值与试验值对比Table 5 Comparison of calculated and experimental values bending moment of hybrid FRP reinforced beams

5 结束语

本工作运用有限元软件建模并分析FRP筋种类、混凝土强度、等效配筋率等因素对混杂FRP筋梁抗弯性能的影响,建立了混杂FRP筋梁适筋破坏时FRP筋应力表达式,并给出混杂FRP筋梁抗弯承载力的计算公式.本工作得出以下结论:

(1)建立了混杂FRP筋梁有限元分析模型.数值分析结果表明:等效配筋率对混杂FRP筋梁的承载能力和变形性能影响最为显著,其次为FRP筋种类,而混凝土强度对承载力有一定的影响,但对刚度影响较为有限.

(2)在混凝土强度、等效配筋率相同的情况下,通过改变FRP筋种类难以兼顾承载能力和延性性能.

(3)建立了混杂FRP筋梁适筋破坏时FRP筋应力表达式,并给出混杂FRP筋梁抗弯承载力计算公式,基于该文FRP筋应力表达式能够较为准确地计算其抗弯承载力.

(4)FRP筋应力表达式中有回归分析确定的参数,需要大量的试验数据校核,且公式只考虑了部分影响因素,需要进一步研究.