基于混合重构高阶间断伽辽金方法的二维层流和湍流数值模拟

熊 为,张卫国,丁 珏,杨小权,翁培奋

(1.上海大学力学与工程科学学院,上海 200444;2.中国空气动力研究与发展中心旋翼空气动力学重点实验室,四川 绵阳 621000)

目前,基于二阶精度数值格式求解雷诺平均Navier-Stokes(Reynolds-averaged Navier-Stokes,RANS)方程的方法得到了广泛应用,定常湍流流动问题已经得到了很好的数值解决.但是,基于高精度精细化的湍流数值模拟依然发展缓慢.高精度有限元方法以间断伽辽金(discontinuous Galerkin,DG)有限元方法为代表,构造单元间分段的多项式解函数,仅增加解函数的自由度就能提高求解精度,因此具有较大的发展前景.相对于有限体积方法,基于有限元方法的间断伽辽金方法本身存在不足,即处理相同的网格数量时,间断伽辽金方法需要求解一个含有更多变量的矩阵方程组,从而导致间断伽辽金方法在进行流场计算时通常需要消耗大量的计算资源和内存资源.

已有很多研究致力于降低间断伽辽金方法在计算资源方面的消耗.Dumbser等[1-2]引进了一系列重构间断伽辽金(reconstructed discontinuous Galerkin,rDG)方法的思路,以PnPm格式为标志提出了第一个重构间断伽辽金方法,即最小二乘复原方法(least-square recovery method),其中Pn代表用于估计间断伽辽金方法所求守恒量的解时,使用分段多项式的阶数为n;而Pm则代表重构的分段多项式的阶数为m.Dumbser等[1-2]的工作是依据文献[3-4]提出的在单元内进行复原(recovery)的思路展开的.在使用最小二乘复原方法获得多项式解时,认为重构多项式与相关控制体单元里间断伽辽金方法直接获得的解在弱形式上相同.最小二乘复原方法不仅对于单元内均值,而且对于单元内所有的高阶矩都保证了较高程度的守恒性.然而,高守恒性的最小二乘复原方法在计算资源方面消耗比较高,同时重构过程依赖相邻网格信息,在处理边界附近网格单元时,会由于相邻单元数目不足而降低重构的精度.Luo等[5]和Xia等[6]提出了基于泰勒基函数,可在任意网格上用于求解可压缩Euler方程和Navier-Stokes方程的最小二乘重构方法(least-square reconstructed method).这种重构方法对相邻单元中心点的值和导数进行插值,从而得到新的多项式方程.这类方法只在von Neumann相邻单元上进行重构,因此格式相对而言具有紧致性、简单性、鲁棒性和可塑性,并且能够保证较为精确的变量守恒性,包括单元内均值和泰勒基函数导数的守恒性.然而,此类重构方法无法保证2-exact的特性.为此,Cheng等[7-8]提出了在任意网格上针对可压缩流动的混合最小二乘重构方法(hybrid least-squares reconstructed methods).该方法综合了最小二乘点值重构和最小二乘积分重构的优点,确保了计算精度满足2-exact的特性.在高阶重构方法中,黏性项的离散大多采用第二Bassi-Rebay(second Bassi-Rebay,BR2)格式,但是传统方法没有考虑BR2格式局部和全局提升算子高阶重构量的贡献,这势必会对计算精度造成一定的损失.

基于上述讨论,本工作在混合最小二乘重构方法的基础上,发展三阶重构的BR2格式黏性数值通量的重构间断伽辽金方法,用于求解可压缩Navier-Stokes(NS)方程和RANS-SA(Reynolds averaged Navier Stokes-Spalart Allmaras)系统方程.通过典型算例,着重分析混合重构的rDGP1P2方法的计算效率、计算精度和收敛性.

1 控制方程

为了提高计算精度以及数值稳定性,本工作根据文献[9-10]将RANS方程和一方程Negative Spalart-Allmaras湍流模型方程耦合成为系统方程,

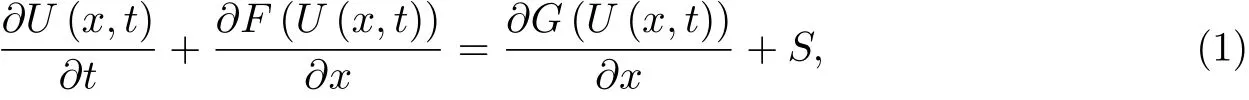
式中:守恒向量U、对流项通量F、黏性项通量G和源项S的表达式分别为

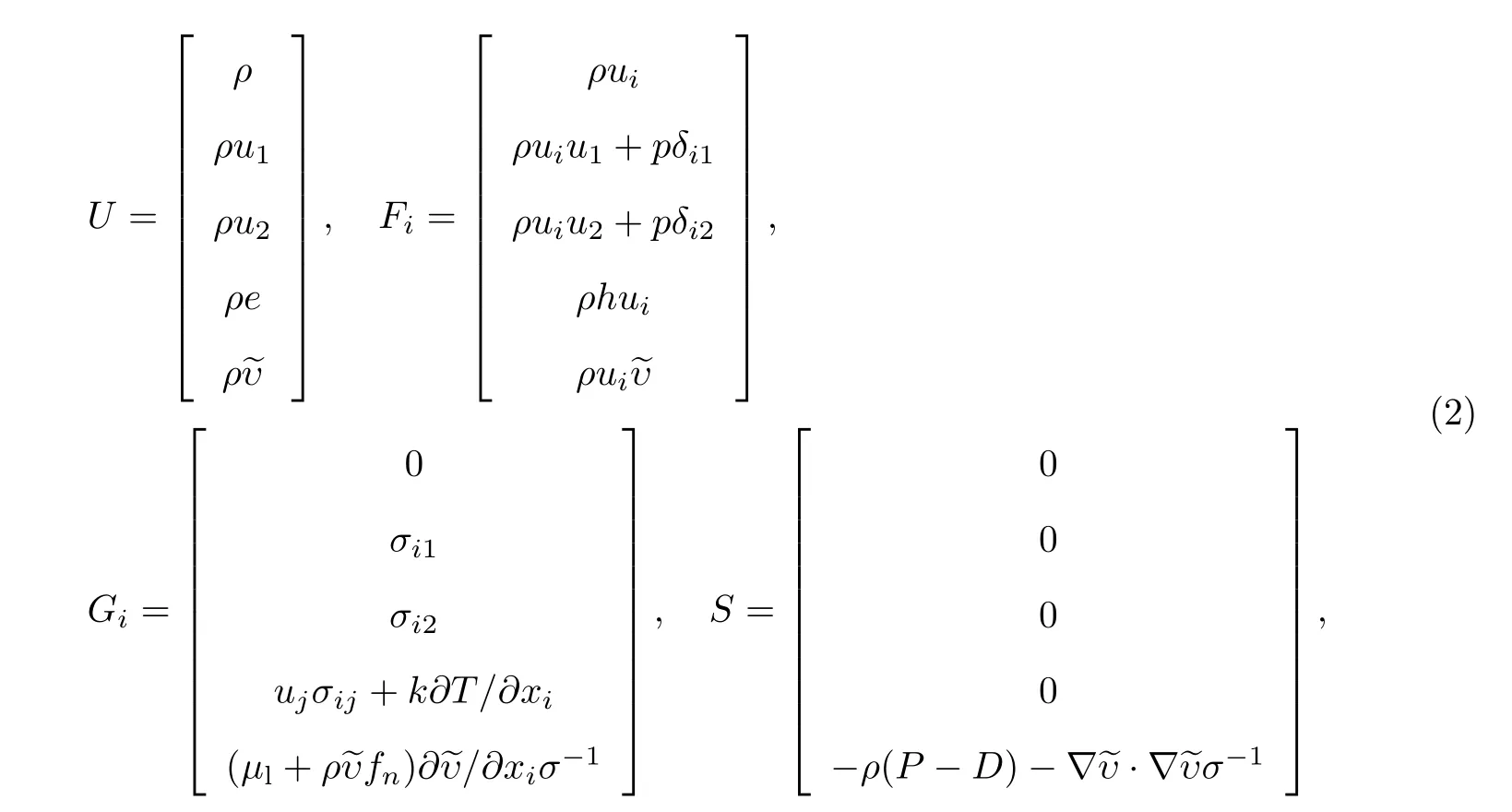
其中压力p可以由状态方程得到,

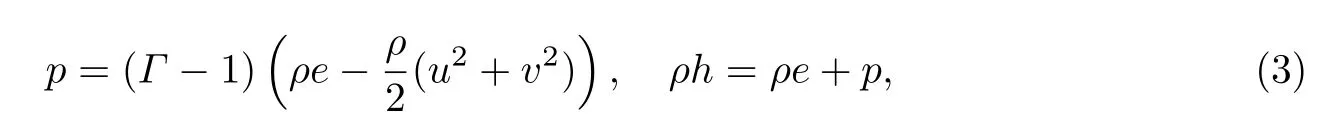
Γ取1.4.应力分量为

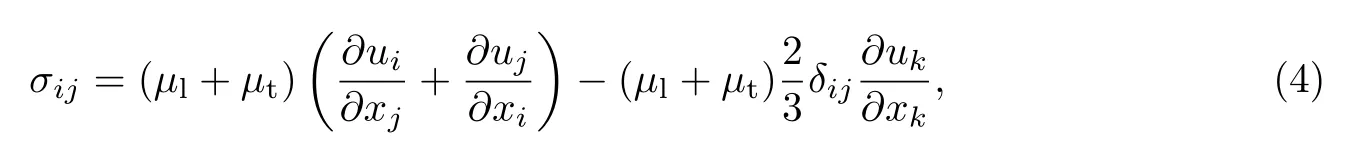
式中:δij是Kronecker符号;k是流体的热传导系数.

湍流模型中的生成项P和破坏项D分别为

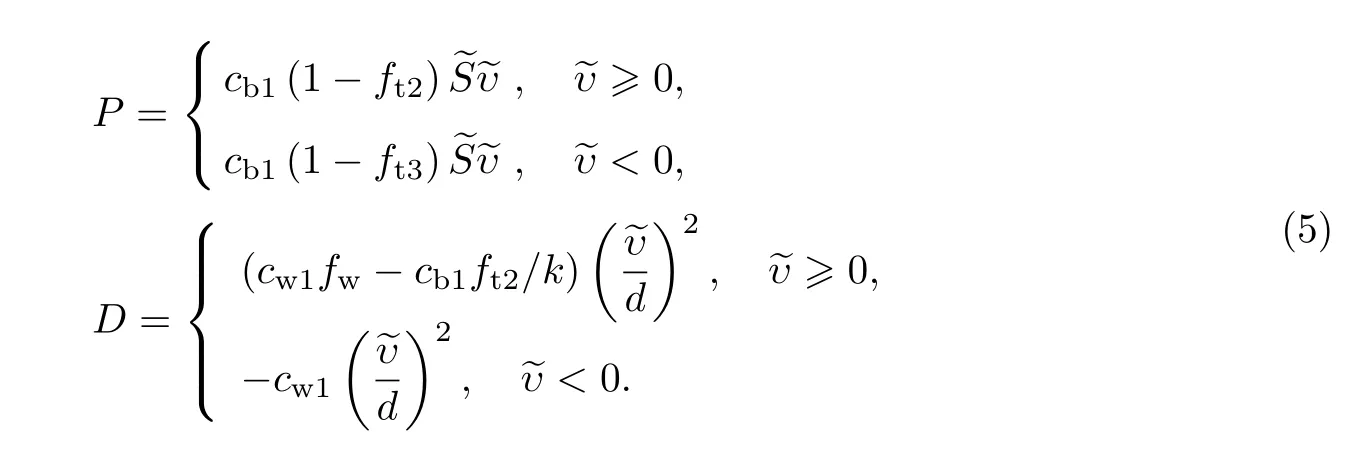
涡黏性系数μT的定义为

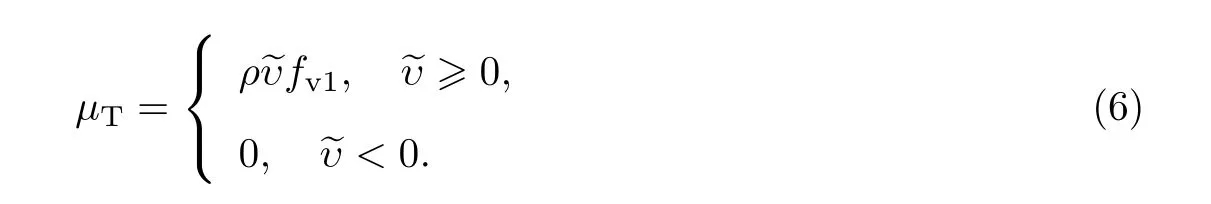
修正的涡量~S为

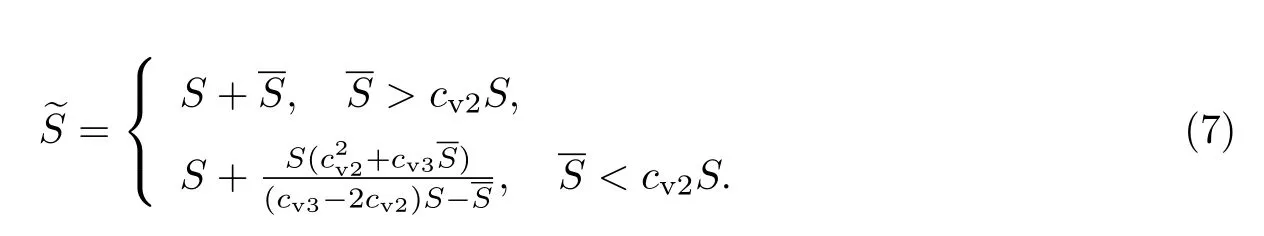
其他参量请参考文献[9-10].对于层流算例只求解NS方程,不考虑SA湍流模型.

2 重构的间断伽辽金方法

2.1 间断伽辽金方法

方程(1)弱积分下的DG方法可表示为

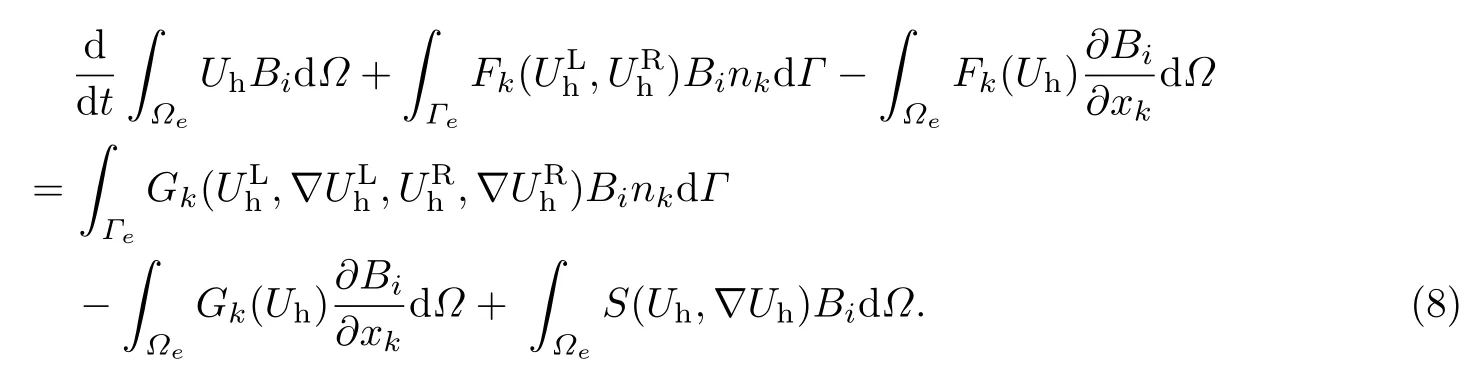
黏性通量离散采用BR2格式[11],该格式的形式如下:

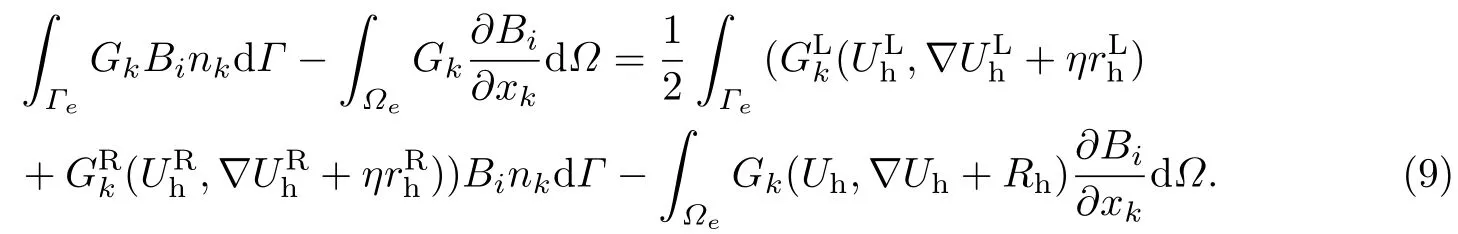
为了保证格式的稳定性,η取1～6.r为局部算子,R为全局算子,定义

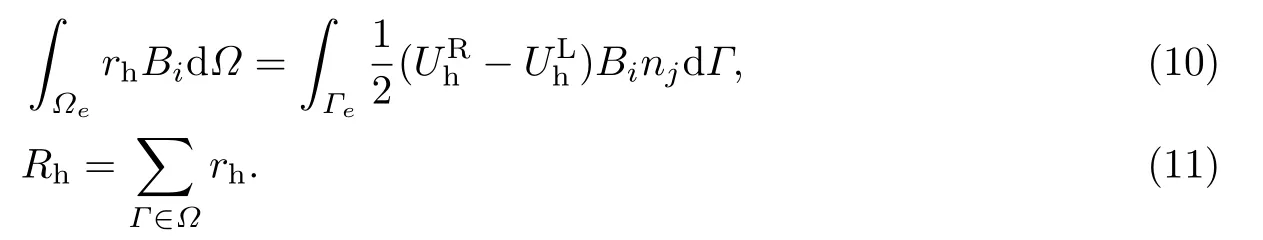
两种算子的离散形式为

其中

式(12)中Uh可近似为

基函数Bi(x)采用Xia等[6]提出的Taylor基函数.

2.2 混合高阶重构方法

在传统DG方法中,方程(5)的各阶导数是通过求解方程组(4)得到的.三阶数值模拟由于矩阵规模巨大,导致计算时间长,且占用大量内存.为了减少计算量,进一步提高计算效率,本工作采用重构方法,即自由度中的平均值和一阶导数通过传统的DG方法求得,而二阶导数则采用重构的方法获得,同样可以达到三阶精度.

文献[7-8,12]发展的混合最小二乘重构方法兼容了积分重构方法和点值重构的优点,即平均值的计算采用积分方程,其余采用点值导数.该方法的优势是计算效率高于传统DG方法且满足2-exact特性,使得非均匀网格能够达到三阶精度.具体做法如下:

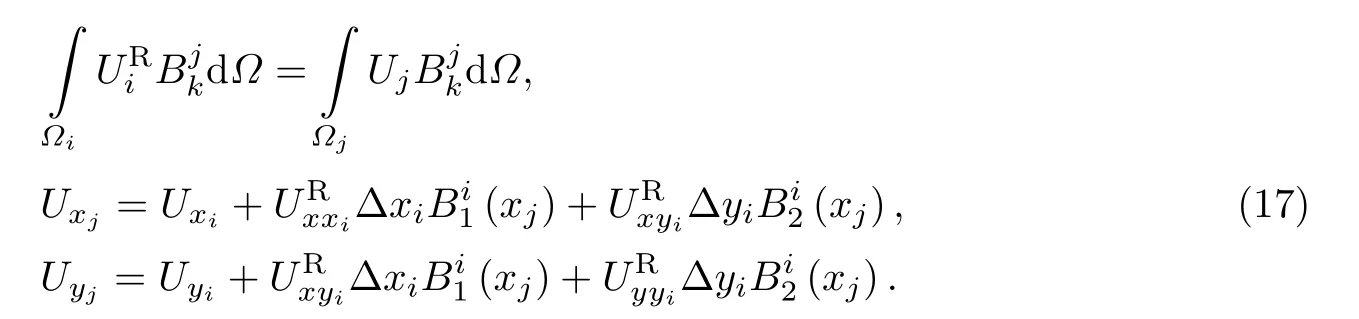
在混合最小二乘重构方法中,重构以后的UR不是间断伽辽金方法中单元中心点的值,而是将单元内平均值作为重构间断伽辽金方法解向量多项式的第一个自由度,而解向量根据相邻单元内平均值进行重构.利用与控制体单元i拥有公共面的单元j,建立如下关系式:

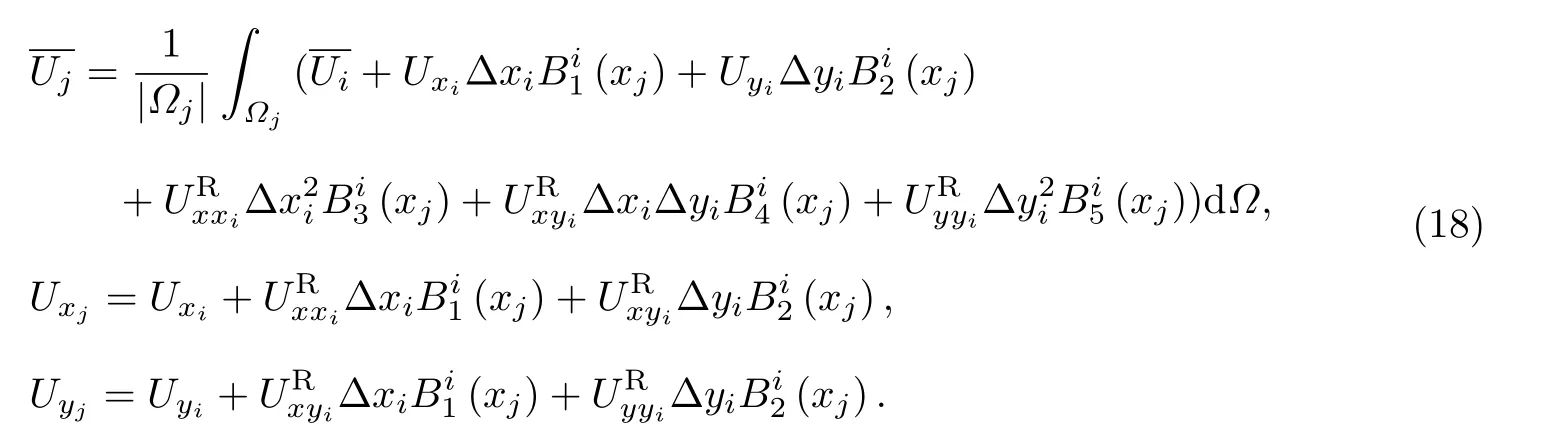
式中:R为重构方程组右端项.方程(19)左乘系数矩阵的转置,得到线性方程组

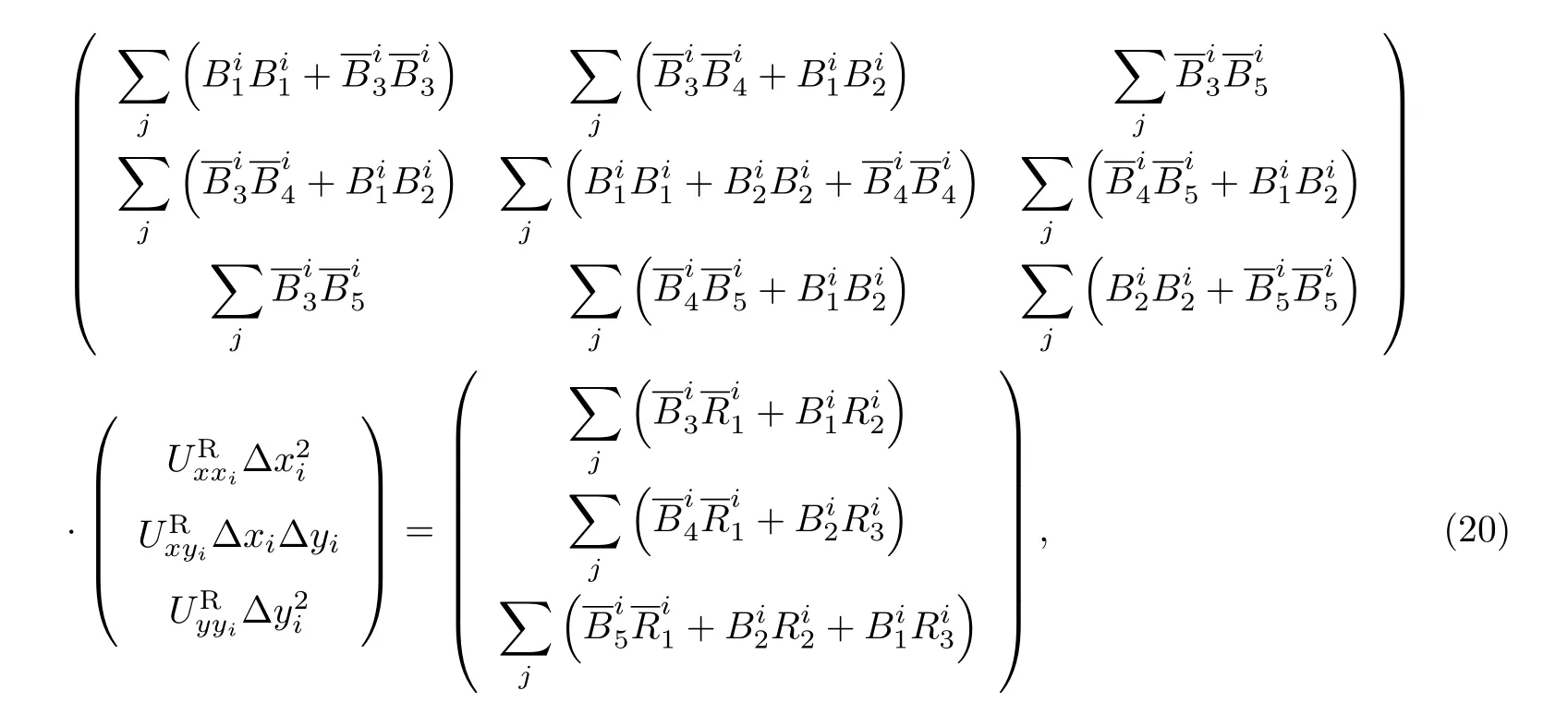
其中

线性方程组(20)直接求解即可,无需进行迭代求解.对于间断伽辽金方法,如果进行最小二乘重构,需要对中心点进行插值.而混合最小二乘重构方法用单元内守恒量的平均值进行多项式重构,满足2-exact特性,保证了求解守恒量方程的精度.

当采用BR2格式进行黏性项离散时,在传统rDGP1P2的BR2计算中,局部提升算子和全局提升算子均采用P1分布.为了进一步提高计算精度,本工作对两类提升算子均采用P2多项式分布.具体表达式如下:

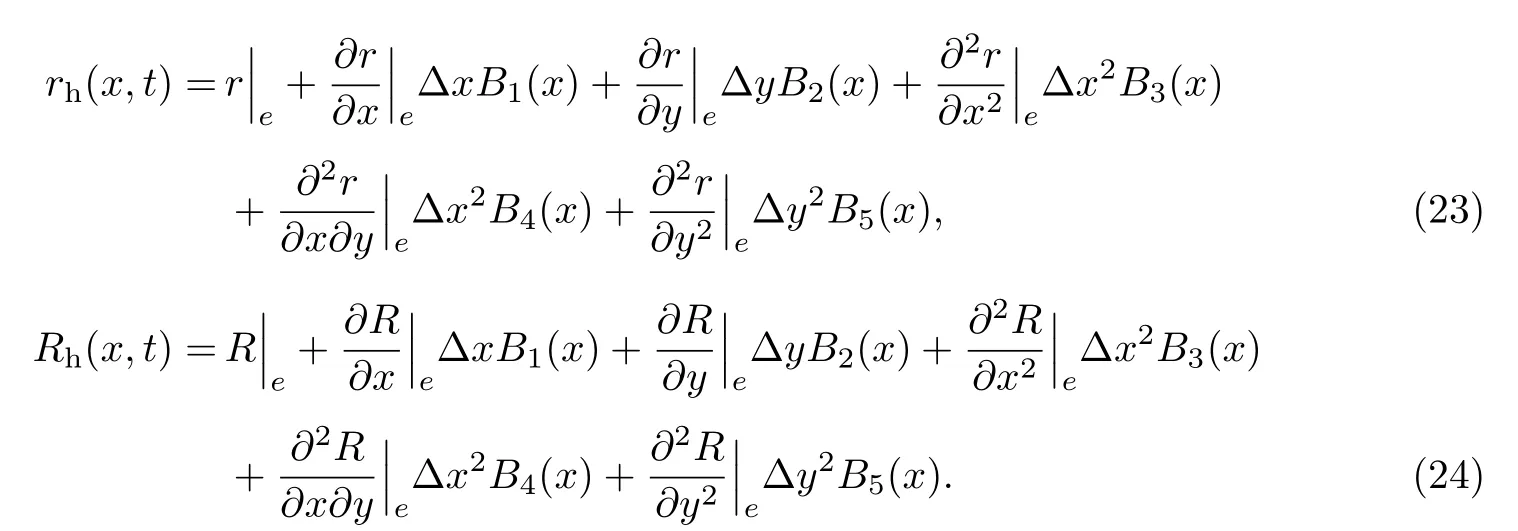
结合对守恒量进行重构的方式,对BR2格式的提升算子进行重构,用低阶导数项求解高阶导数项.

2.3 隐式时间推进格式

方程(8)写成半离散形式为

式中:M是质量矩阵;U是解矢量;R是右端残值.R包括无黏通量、黏性通量和它们对应的域积分项,这里无黏通量的求解采用Harten-Lax-van Leer接触(Harten-Lax-van Leer contact)格式[13],黏性通量的求解采用BR2格式[11].

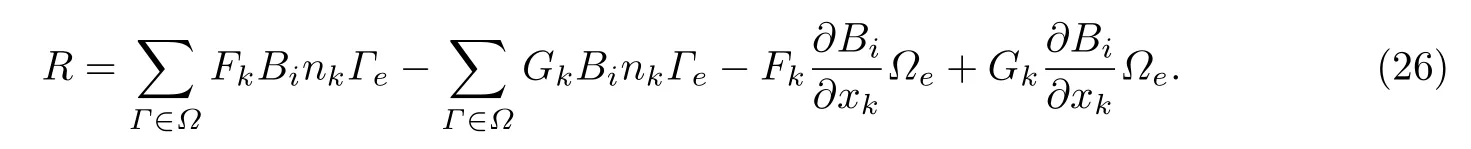
方程(25)线化后可以表示为

式中:∂Rn/∂U是Jacobian矩阵;Δt是当地时间步长.当Δt趋于无穷大时,系统方程的求解就变成了典型的牛顿迭代.

在通常情况下,Jacobian矩阵的重构方法模板比较宽泛,很难精确求解.主要存在的问题是,重构的高阶导数对应的贡献很难准确得到.为了尽可能地提高Jacobian矩阵的精度,本工作在处理Jacobian矩阵时考虑BR2格式局部提升算子和全局提升算子中高阶导数的贡献部分.除此之外,对平均值和一阶导数的Jacobian可精确求解(即P1的精确Jacobian和局部提升算子、全局提升算子对二阶导数的贡献).另外,壁面边界、远场边界等边界上对应无黏和黏性数值通量的Jacobian矩阵依然给出了P1的精确求解.

对于定常问题,方程(21)的求解采用基于上-下对称高斯赛德尔格式(lower-upper symmetric Gauss-Seidel scheme,LU-SGS)预处理的广义极小剩余(generalized minimal residual,GMRES)方法;对于非定常计算采用四步隐式Runge-Kutta方法[14]求解,其中隐式子迭代同样采用基于LU-SGS预处理的GMRES方法进行求解,子迭代的设置为10步或残值下降3个量级.

3 算例分析

3.1 二维平板层流流动

二维绝热平板层流的自由来流马赫数为Ma∞=0.2,雷诺数为Re=1×105.计算域为[-0.5,1.0]×[0,1.0],其中底部[0,1.0]为无滑移边界条件,底部其余部分为滑移边界条件;其他边界为特征边界.分别采用三角形(2 400个单元)、四边形(1 200个单元)和三角形/四边形混合(1 800个单元)网格进行计算,如图1所示.

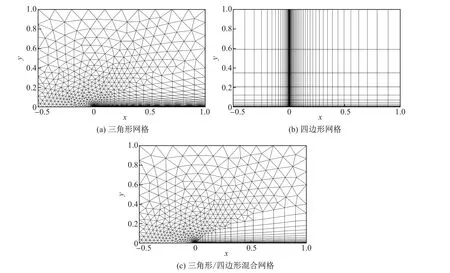
图1 平板层流计算网格Fig.1 Grid of laminar flow over a flat plate

图2给出了平板层流流动表面摩擦力的常用对数在x方向的分布.基于PnPm格式重构间断伽辽金(rDG)方法,将rDGP1P2和DGP1方法的计算结果与Blasius近似解进行比较.表面摩擦力分布显示,rDGP1P2方法的求解结果与Blasius解吻合很好;与DGP1方法相比,rDGP1P2方法的计算结果与Blasius解吻合得更好.图3给出了平板层流流动在混合网格上的密度残差收敛曲线.由图可知,DGP1方法的收敛需要迭代25步,rDGP1P2方法的收敛需要迭代28步,可见rDGP1P2方法在提升求解的精度基础上,迭代步数和DGP1相当.

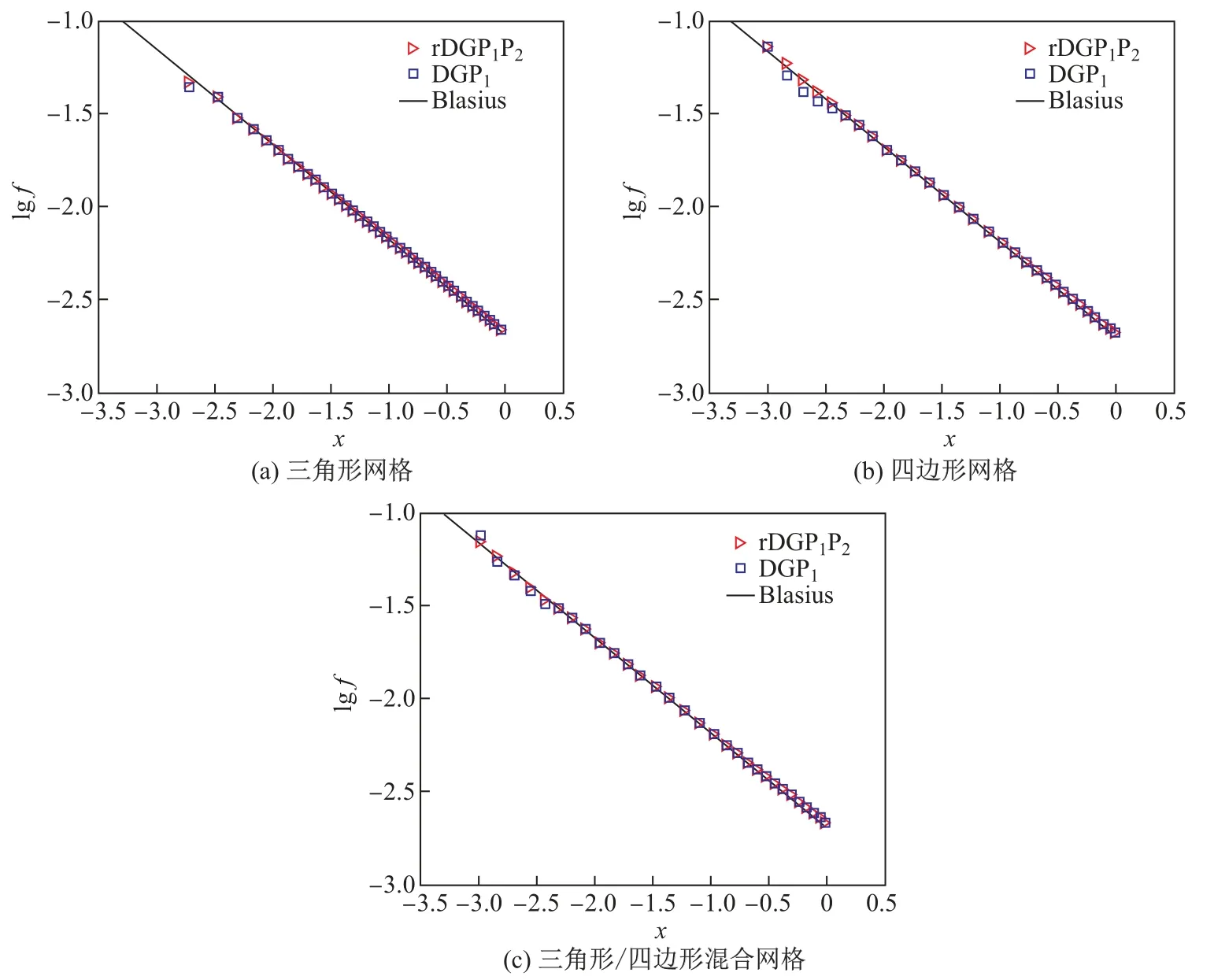
图2 平板层流流动计算表面摩擦力对数分布Fig.2 Logarithmic skin friction coefficient of laminar flow over a flat plate

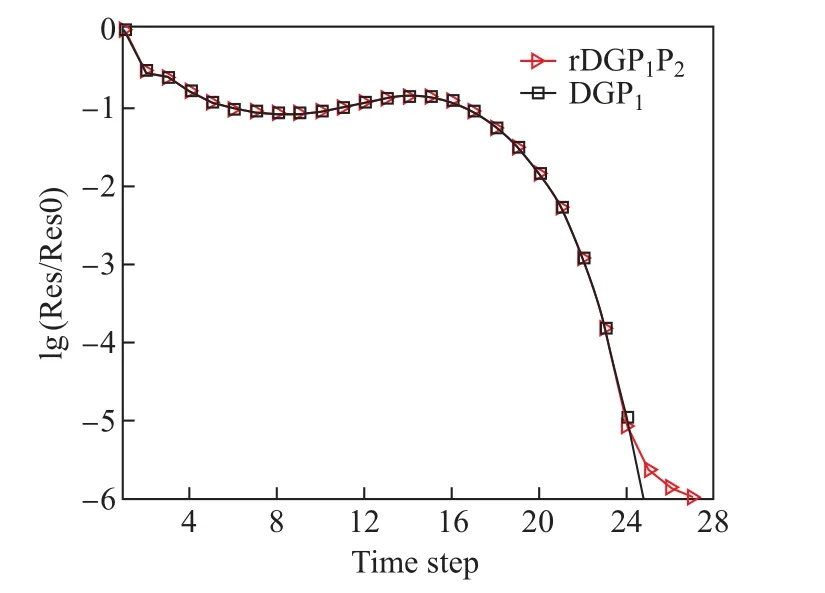
图3 平板层流流动计算密度残差曲线(混合网格)Fig.3 Convergence histories for density of laminar flow over a flat plate(hybrid mesh)

与二阶精度的DGP1方法相比,三阶DGP2方法提高了精度阶数,守恒量多项式的自由度从3个增加到6个,对应求解时每个单元的自由度由原来的3×3(一阶三角形网格)或4×3(一阶四边形网格)分别变为3×6和4×6.理论上,应用传统DG方法时,三阶精度模拟比二阶精度模拟的计算量增大一倍,每个时间步长消耗的平均CPU时间也增加一倍.在DGP1(二阶)基础上重构的P2格式,即DGP1P2具有三阶精度,但是每个单元上求解的自由度只有3个,因此计算量大幅度减小.表1给出了二维平板层流数值算例下rDGP1P2方法和DGP1方法的单步长平均CPU时间.由表可知,rDGP1P2方法每个时间步长消耗的平均CPU时间与DGP1方法相当,且与网格数、网格类型或控制方程类型均无关.通过混合重构,具有三阶精度的rDGP1P2额外的3个自由度可利用二阶(P1)精度通过求解一个较小的矩阵得到,在提高计算精度的同时,提高了高精度数值方法的计算效率.

表1 二维平板层流流动单步长平均CPU时间(单位:秒)Table 1 Average CPU time of each step of laminar flow over the plate(Unit:s)

3.2 Bump湍流流动

二维Bump湍流的自由来流马赫数为Ma∞=0.5,雷诺数为Re=3×106.计算域为[-25.0,25.0]×[0,5.0]的矩形通道,底部[0,1.5]为带有对称凸起的无滑移壁面边界条件,上下面其余部分为滑移壁面边界条件,入流和出流为特征边界条件.计算中分别采用2种四边形网格进行数值计算,粗网格和细网格的节点数分别为11 495和53 361,网格单元数分别为52×54和110×120,其中粗网格以及对应的Bump区域局部放大网格如图4所示,细网格仅对该结构按比例加密.

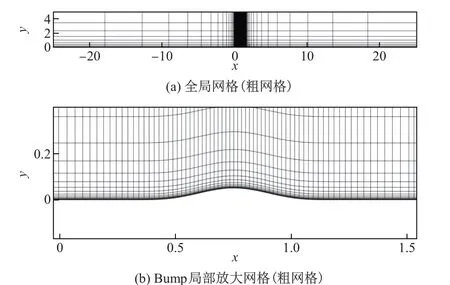
图4 Bump湍流流动网格Fig.4 Grid of turbulent flow over the Bump

图5显示2种四边形网格下,rDGP1P2和DGP1方法计算的Bump湍流流动涡黏度等值线.由图可知,随着网格密度的增加,rDGP1P2方法和DGP1方法所得的涡黏度计算结果均更加稳定和光滑.图6给出Bump表面摩擦阻力系数曲线.由图可见,Bump顶端的摩擦阻力系数有略微的数值振荡现象,且随着网格加密振荡消失.图7给出rDGP1P2方法和DGP1方法求解Bump算例得到的密度残差收敛曲线.当残差下降6个数量级时,rDGP1P2方法需要迭代249时间步,DGP1方法需要迭代187时间步,两种方法的迭代时间步数略有差别.对比计算效率与精度,rDGP1P2方法单步的计算时间与DGP1方法相当,但是rDGP1P2方法在粗网格上的收敛解与DGP1在细网格上的收敛解基本一致,这说明rDGP1P2方法的计算精度高于DGP1方法.

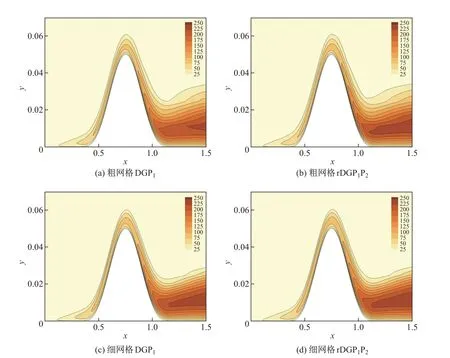
图5 Bump湍流流动涡黏度云图Fig.5 Contours of vortex viscosity of turbulent flow over the Bump

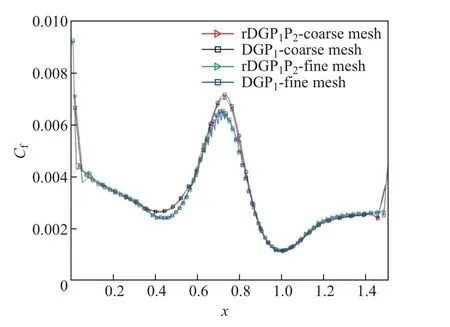
图6 Bump湍流流动表面摩擦阻力系数Fig.6 Skin friction coefficient of turbulent flow over the Bump

图7 Bump湍流流动计算密度残差曲线(粗网格)Fig.7 Convergence histories for density of turbulent flow over the Bump(coarse mesh)

3.3 非定常圆柱绕流层流流动

非定常圆柱绕流层流流动的自由来流马赫数为Ma∞=0.2,雷诺数为Re=200.特征长度选取圆柱的直径,圆柱壁面采用无滑移壁面边界条件,远场采用特征边界条件.计算网格采用二阶全单元网格,包含8 406个三角形单元和4 568个四边形单元,如图8所示.计算采用四阶显式单对角隐式Runge-Kutta(explicit singly-diagonal implicit Runge-Kutta,ESDIRK)[14]进行时间推进,Δt=0.5,共计算2 000个时间步长.

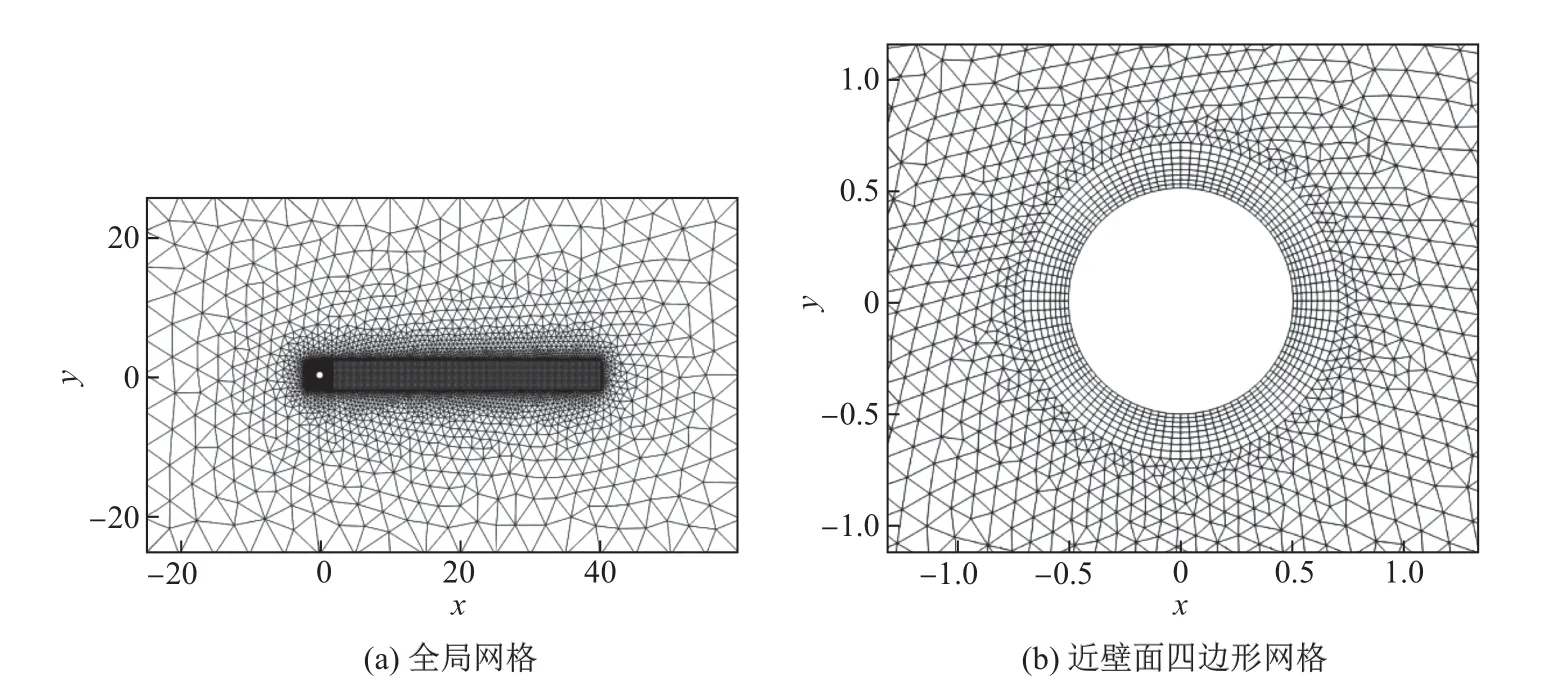
图8 二维非定常圆柱绕流层流计算网格Fig.8 Grid of 2-dimensional transient laminar cylindrical winding flow

图9给出了rDGP1P2重构方法计算t=1 000时刻的马赫数云图和熵云图.由图可见,对于非定常圆柱绕流层流,用基于BR2格式黏性通量离散的rDGP1P2方法能够准确地捕捉层流的涡街结构.图10给出rDGP1P2方法和DGP1方法计算所得的升力系数和阻力系数,横坐标为无量纲时间.由图可见,随着时间的推进,非定常涡结构体现为某一定频率的升阻力变化周期现象,与实际情况相符;同时,rDGP1P2方法和DGP1方法求解的升阻力系数曲线幅度和频率吻合程度较高,验证了混合重构BR2间断伽辽金方法在非定常数值计算中的算法稳定性和程序可靠性.

图9 二维非定常圆柱绕流层流计算马赫数和熵分布云图Fig.9 Contours of Mach number and entropy of 2-dimensional transient laminar cylindrical winding flow

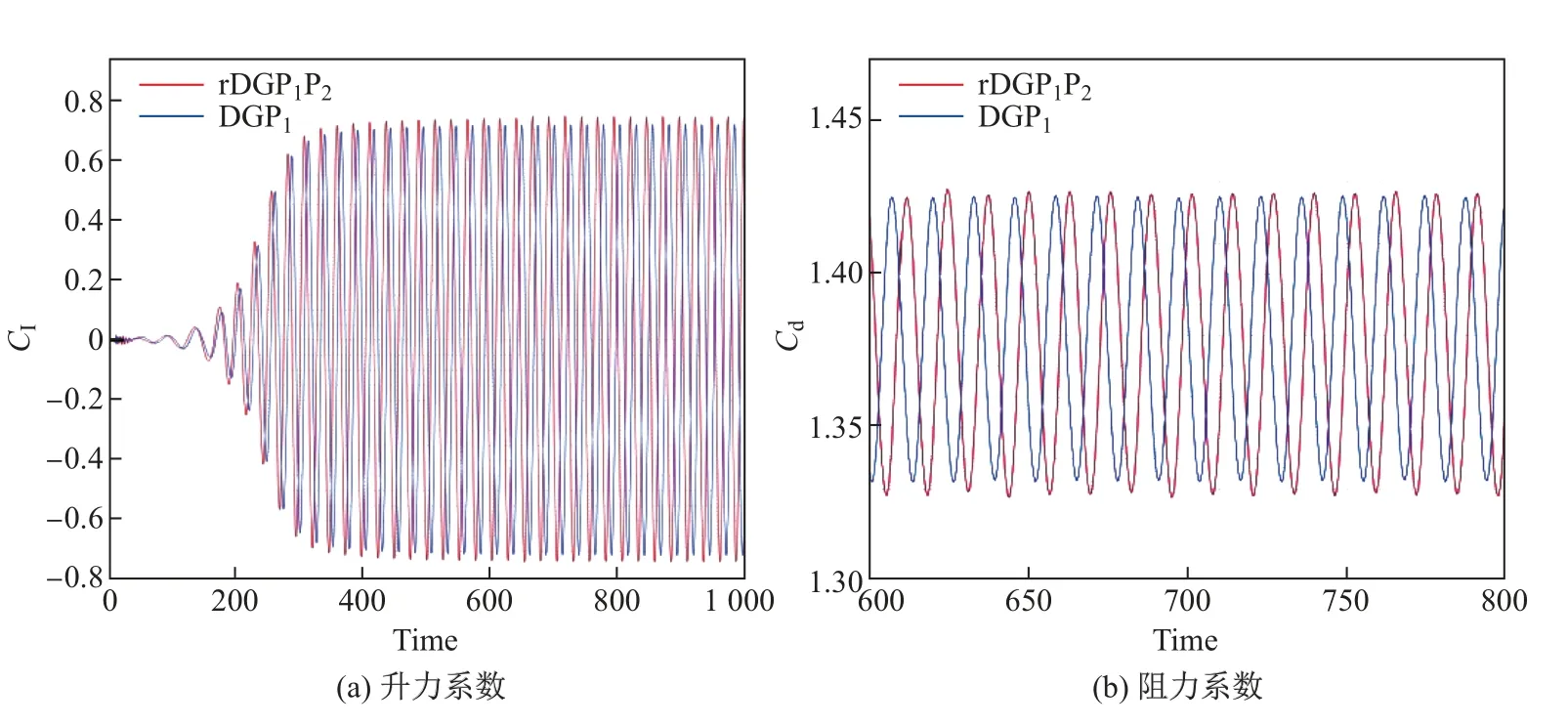
图10 二维非定常圆柱绕流层流计算升力系数和阻力系数Fig.10 Lift and drag coefficient of 2-dimensional transient laminar cylindrical winding flow

4 结论

针对三阶精度传统间断伽辽金方法求解NS方程和RANS方程自由度多、运算量大等特点,本工作综合利用点值重构和积分least-squares重构方法的优势,并结合BR2黏性通量求解格式,发展了基于BR2格式的三阶混合重构间断伽辽金方法rDGP1P2.通过层流和湍流典型算例验证了发展的rDGP1P2方法的计算精度、计算效率和收敛性,所得结论如下.

(1)rDGP1P2方法在P1自由度的基础上通过运算量相对少的混合重构使计算精度由二阶提高到三阶,从而大幅度减少运算量,提高了计算效率.

(2)发展的rDGP1P2方法具有良好的收敛性,能够满足层流、湍流和非定常流动数值模拟的要求.

(3)发展的混合重构间断伽辽金方法不仅能够用于层流流场的计算,而且能够用于湍流流场的数值模拟,数值计算结果和实验结果吻合较好.