基于正态分布概率模型的渗滤液回灌影响分析

侯 娟, , ,鲍仕芬,刘 磊

(1.上海大学力学与工程科学学院,上海 200444;2.School of Engineering,University of Virginia,VA 22904,Charlottesville,USA;3.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室,武汉 430071)

城市生物固体废弃物填埋场,因其良好的环保性能和经济效益,越来越受到环境岩土工程界的广泛关注[1-2].虽然填埋场能产生甲烷等清洁性气体,具有良好的经济效益,但同时也对城市固体废弃物的稳定性提出了更高的要求.为了提高固体废弃物的稳定性,加速填埋场稳定化进程,提高填埋场的使用效率,众多学者提出了通过回灌地下水、渗滤液以及氧气等加速垃圾体分解的方法[3].大量试验研究表明,适量的渗滤液回灌能有效加速废弃物的降解,进而提高填埋场的稳定化进程[4],其中渗滤液回灌量是影响填埋场稳定性的关键因素.回灌渗滤液过少将难以达到生物分解的目的,而过量又会降低垃圾体的抗剪强度,从而降低填埋场边坡的安全系数.此外,渗滤液水头过高对底部衬垫系统将产生超覆荷载[5].因此,准确设计渗滤液回灌系统对于提高填埋场的稳定性具有十分重要的意义.

目前,生物固体废弃物填埋场渗滤液的回灌主要分为地表回灌和地下回灌.地下回灌主要集中在垂直井和排水毯等回灌方式[6].周新华等[7]建立了二维降解-渗流-温度耦合模型,研究了不同回灌参数下垃圾土的降解速率.研究结果表明,高回灌频率更有利于填埋场加速进入稳定阶段.Haydar等[8]和Jain等[9]将垃圾体视为均匀介质,使用水平井对生物填埋场进行渗滤液回灌,研究了回灌量、回灌频率和回灌时间等参数对含水率的影响.McCreanor等[10-11]在考虑垃圾体均质的情况下,研究了渗滤液回灌频率对回灌结果的影响.Jain等[12]通过竖直井研究了均质情况下渗滤液回灌影响范围与注射压力头、回灌频率、回灌量、回灌时间、垃圾体渗透系数等因素之间的关系.Kahire等[13]基于HYDRUS-2D建立了单孔隙度均质模型,研究了垃圾体水压和横向影响宽度与固体废弃物、垂直井回填物的渗透系数、垂直井的直径以及渗滤液收集系统的关系.结果表明,在给定流量的情况下,垂直井的直径、回填物的渗透系数对横向宽度几乎没有影响,而随着垃圾渗透系数的增加,横向影响宽度逐渐减小.Feng等[14]在考虑了垃圾体分层的基础上,提出了可以表征垃圾体压缩和沉降对孔隙度影响的二维沉降模型,研究了渗透率、压实程度、初始孔隙度和注入强度对含水率的影响.结果表明,分层和压实度对垃圾体含水率有很大影响,渗滤液回灌的影响深度随着初始孔隙度和注入强度的增加而增加.已有的这些研究,主要是将垃圾体视为均匀介质来研究渗滤液的运移规律.尽管个别研究考虑了横纵向渗透系数造成的差异,但就整个垃圾体的非均质性对渗滤液运移规律影响的研究还较少.

为了研究更贴近真实情况的渗滤液运移规律,在考虑垃圾体非均质性的基础上,本工作以武汉北洋桥垃圾填埋场为原型,使用COMSOL Multiphysics®软件[2],基于Richard’s方程,研究了水平井在考虑垃圾体渗透系数随机正态分布情况下的运移规律,并就横纵向渗透系数比值、回灌速率以及回灌时间等对回灌效果的影响进行了比较.同时为了进一步探究渗滤液的运移规律,考虑了工程实际(即现场含水率传感器一般埋设在距回灌井1 m,且该位置含水率变化较为明显)[15],对距回灌井横纵向1 m处探测点的含水率,以及回灌达到100 d时,含水率大于0.45(最优含水率)的最大横向影响范围进行了研究.结果发现,该含水率下垃圾体降解速率最快,且观察较为明显.最后,将各影响因素下该探测点的含水率与现场数据进行了对比,确定了该工况下的横向影响范围,并以大于最优含水率(0.45)的横向影响范围为准[9],给出了设置回灌井间距和数量的参考值.

1 数值模拟模型构建

有限元软件COMSOL Multiphysics®能够有效模拟温度、应力和渗流等多场耦合作用下的情况,其中地下水流模块可以模拟溶液在饱和及非饱和多孔介质中的流动.同时基于Richard’s方程,可以有效模拟渗滤液在非饱和垃圾体中的运移规律.

1.1 控制方程

垃圾体渗滤液液面以上为非饱和介质.由Richard’s方程可知,非饱和区域的渗滤液渗透系数与该区域的体积含水率和饱和度直接相关[16].基于质量守恒定律,有

式中:θ是含水率;ρ是渗滤液的密度(kg/m3);vx、vy、vz分别是x、y、z方向的流动速率(m/s).

式(1)的右边可以变换为

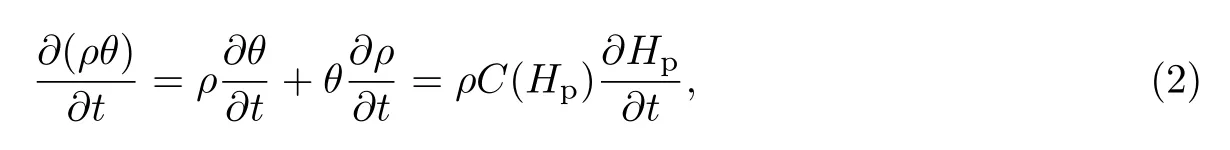
式中:

Hp是压力水头(m);C(Hp)是单位容水度(m-1).

式(1)的左边可以变换为

式中:Hp是压力水头(m);k(Hp)是垃圾体的非饱和渗透系数(m/s).

综合式(1)～(4),可以得到渗滤液在垃圾土中运移的方程为

式中:Hp是压力水头(m);C(Hp)是单位容水度(m-1);k(Hp)是垃圾体的非饱和渗透系数(m/s);z是纵向深度(m).

垃圾体中非饱和区域的渗透系数与孔隙度及含水率直接相关.孔隙结构的曲折度及垃圾体的基质吸力等均会降低渗滤液所能经过的孔隙大小.垃圾体内水-汽液面就类似于土颗粒表面.当垃圾体中渗滤液可流过的空间减少时,非饱和区域的渗透系数也随之减小.因此,非饱和区域的渗透系数可以表示成饱和渗透系数与含水率之间的关系,即

式中:k(θ)是非饱和渗透系数;ksat是饱和渗透系数;kr(θ)是相对渗透系数.

Van-Genuchten[17]提出了V-G模型,该模型可以表征土的含水率与压力水头之间的特征曲线,适用于描述垃圾体中渗滤液的运移过程[18-20].kr(θ)主要通过以下V-G模型获得,即

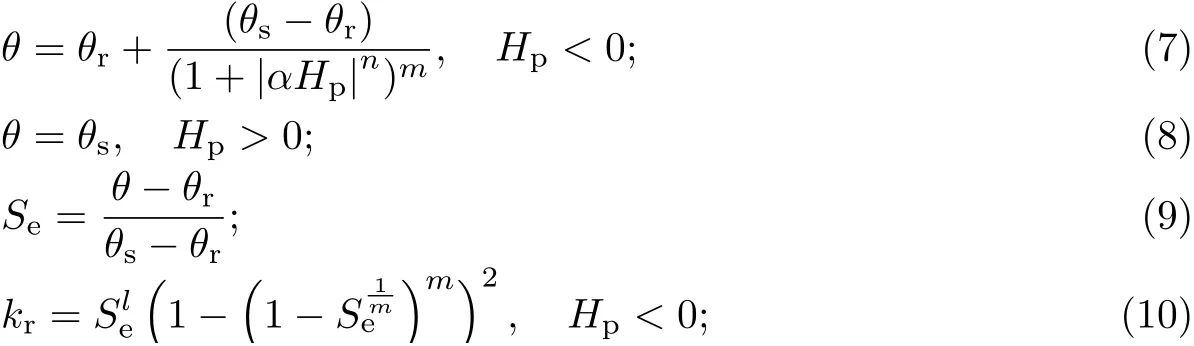
式中:θ是含水率;θr是残余含水率;θs是饱和含水率;α是进气压力的倒数;Se是有效饱和度;n是与土的孔径分布有关的系数;l是本构关系常数;m与土体特征曲线的整体对称性有关,m=1-1/n.本工作中V-G模型参数的详细取值如表1[23]所示,其中初始含水率均为0.38[12].

表1 模拟参数Table 1 Simulation parameters

1.2 正态分布概率模型

受填埋年限、压缩程度以及自身性质差异等影响,垃圾体表现出了明显的非均质性,并对渗滤液运移产生了显著影响.为了描述垃圾体的非均质性,本工作提出了一种正态分布的概率模型来表征渗透系数随位置变化而变化的规律,即将整个垃圾体划分为若干个区域,将一定范围内的饱和渗透系数通过正态分布的形式随机分布到各个区域中.

式中:αk是比例因子;kx,y是各位置处的饱和渗透系数;是整个垃圾体的饱和渗透系数均值;f(x,y)是研究区域各点的概率密度;μ是正态分布的均值,与正态分布的位置有关;σ2是方差,表示该概率函数分布的波动情况.本工作中随机分布的参数μ=-11.4,σ2=0.159,其取值大小与所给垃圾体实际饱和渗透系数范围有关.渗透系数随机分布的状态如图1所示,其中图1(b)表示40 d时垃圾体非饱和渗透系数的状态,红色处表示渗透系数最大,蓝色处表示渗透系数较小.整个垃圾体渗透系数分布的不均匀性充分反映了垃圾体的非均质性.

1.3 边界条件设置

本工作以武汉北洋桥垃圾填埋场为原型,研究了影响渗滤液横向运移范围的因素.由于在实际工程中,水平井的纵向长度远大于水平井的半径,且沿着纵向水平井的截面保持不变(见图2(a)),因此在水平井边界一定影响范围外,可以将该三维问题转化为二维问题建模(见图2(b)),研究渗滤液在垃圾体水平和深度方向的运移规律.

如图2所示,取其中某一断面建立二维图进行模拟研究.水平方向长为40 m,填埋场埋深为20 m,距填埋场顶部有1 m厚的黏土覆盖层,渗滤液液面位于距填埋场顶部7 m的位置处.该填埋场填埋龄期为15～23 a,属于陈旧型垃圾填埋场,库容垃圾量达103.63万t,填埋场非饱和区域的初始含水率在0.38左右.因此,本模拟取初始含水率为0.38.

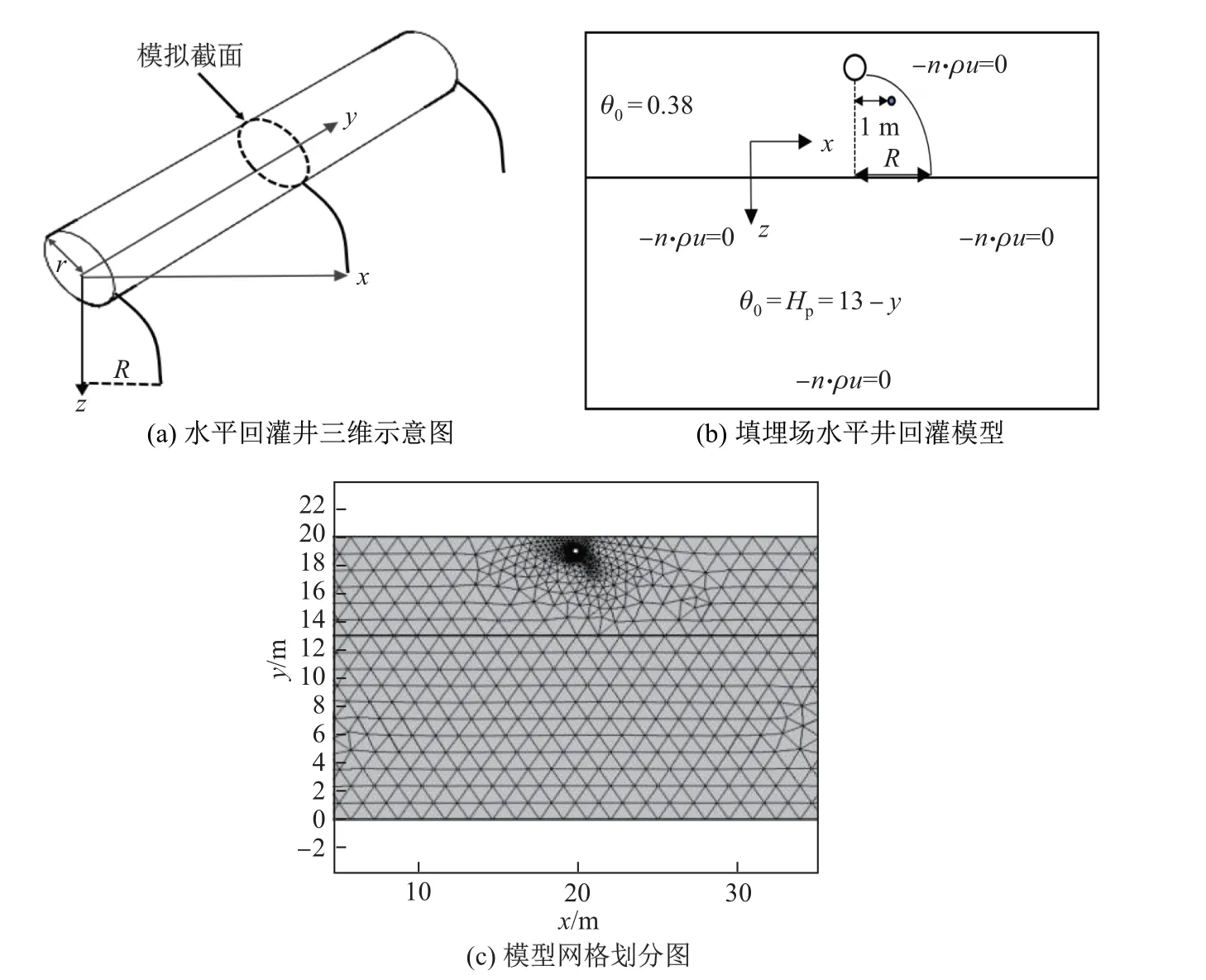
图2 水平回灌井模型Fig.2 Horizontal recirculation well model

根据该填埋场的垃圾成分和填埋年限,在实验室对填埋场垃圾进行了相同比例的配置.室内实验结果发现,该垃圾体的渗透系数约为3.89×10-7～5.33×10-6m/s.因此,本模拟设置垃圾体横向渗透系数为1×10-6m/s,并在3.89×10-7～5.33×10-6m/s范围内设置a为2、5、10共3个梯度的横纵向渗透系数比值.此外,根据现场及室内实验可得,垃圾体的饱和含水率在0.69左右,残余含水率在0.15左右.因此,本模拟取垃圾体的饱和含水率为0.69,残余含水率为0.15.

液面以下为饱和区域,液面以上为非饱和区域.回灌井通过在管壁四周钻入4个大小相同的孔洞模拟,设置该边界为恒定的质量通量边界.填埋场四周是由多层防渗系统做成的防渗结构,为低渗透边界,而垃圾体的上部为1 m厚的黏土覆盖层.不考虑上部降雨等因素对垃圾体内含水率的影响,设置四周的边界条件为无流动边界.

渗滤液的液面是饱和与非饱和区域的分界线,本模拟考虑了填埋场渗滤液液面的影响.液面以上的非饱和区域存在水和空气两种混合流体,二者的压力差值为毛管压强.当取大气压为测量的标准时,上部非饱和带中的水处于小于大气压强的状况,压力水头为负值.液面以下饱和区域的压力水头则为正值,非饱和区域的压力水头为负值,因此设置渗滤液的液面压力水头为0.

1.4 水力参数设置

横纵向渗透系数比值、回灌速率以及回灌时间等是影响渗滤液运移规律的重要因素[21-23].本工作中的具体参数汇总如表1所示.

根据陈旧型垃圾填埋场和新鲜垃圾填埋场的压缩程度不同,设置垃圾体横纵向渗透系数比值a为2、5、10共3个梯度[22-23].此外,回灌速率也是影响渗滤液运移规律的重要因素.当回灌速率较小时,垃圾体对渗滤液的吸附作用会影响其运移速度;而当回灌速率较大时,垃圾体孔隙度和孔隙中的气体也会影响其速度.根据现场回灌使用的最小回灌速率2 m3/(d·m),设置q为2、4、6 m3/(d·m)共3个梯度的回灌速率进行比较[22].同时,回灌时间过长容易使填埋场边坡失稳,而回灌时间过短又会在有限数量的回灌井情况下,无法有效地加速垃圾体降解.回灌时间随填埋场规模大小的不同一般介于10～100 h之间.本工作设置t为10、60、100 h共3个梯度的回灌时间[8,11].

2 结果分析

2.1 单孔隙度均质模型与正态分布模型比较

图3所示为单孔隙度横纵向均质(SU)模型与单孔隙度正态分布(SR)模型在40 d时渗透系数的变化图,其中图3(a)为渗透系数在10-7～10-6m/s时的正态分布变化图,图3(b)为a=10时渗透系数的变化图.对比图3(a)和(b)可知:SR模型下的渗透系数随位置坐标发生变化;在相同时刻同一位置处,SR模型的渗透系数要小于SU模型;随着回灌的持续进行,SR模型的渗透系数逐渐减小(回灌井周围表征渗透系数大小的颜色由浅逐渐变深),而对于SU模型,回灌井周围的颜色最深,表明此时垃圾体为饱和状态,渗透系数为10-6m/s.

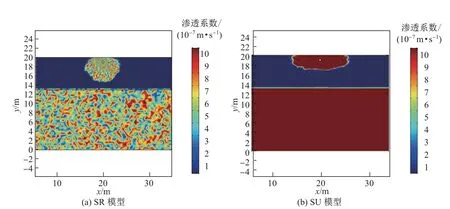
图3 渗滤液回灌40 d时的渗透系数变化Fig.3 Changes of permeability coefficient of leachate recirculation for 40 d

图4给出了SU模型与SR模型下压力水头Hp的变化图.对比SU模型发现,在相同渗透系数范围下,SR模型的横向影响范围较小,但纵向影响深度较大.这说明在SR模型下,横纵向渗透系数的分布更加均匀,其横向渗透系数小于SU模型,而纵向渗透系数则大于SU模型.在100 d时,SR模型下的渗滤液影响区域可到达非饱和区域的底部,在相同时间下其纵向运移速率更快,而横向运移速率较小.该变化趋势更加符合陈旧型垃圾填埋场的特性.因为当陈旧型垃圾填埋场中的垃圾降解到一定程度时,其孔隙分布呈现较为离散的特征,因此其渗透系数大小分布更加离散.

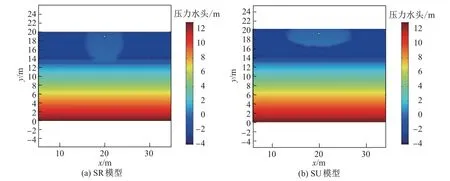
图4 渗滤液回灌100 d时的压力水头变化Fig.4 Changes of pressure head of leachate recirculation for 100 d

2.2 横纵向渗透系数比值的影响

由于陈旧型垃圾填埋场和新鲜垃圾填埋场填埋年限和压缩程度的差异,导致其孔隙度也存在一定的差异,进而影响回灌效果.本工作在控制垃圾体横向渗透系数kh不变的基础上,通过改变a来改变纵向渗透系数kv的大小.设定回灌速率q=2 m3/(d·m),回灌时间t=100 h,其余参数值如表1所示.a为2、5、10共3个梯度下距回灌井1 m处的含水率和横向影响范围如图5(a)和(b)所示.

对比SU模型和SR模型可以发现:二者均呈现含水率先稍微下降,再急剧上升的趋势,直至稳定在饱和含水率峰值一段时间后,含水率又逐渐下降,达到相对稳定状态;随着a的增加,SU模型中探测点达到饱和含水率的时间逐渐增加,由2 d增加到5 d,且其维持在峰值的时间从30 d增加到85 d;随后二者下降的趋势基本保持一致,说明二者的渗透速率此时也保持一致.出现探测点达到饱和含水率的时间随着a的增加而增加这一现象的原因主要如下:当a增加时,垃圾体孔隙减小,kv也逐渐减小,因此渗滤液运移所需的时间增加.观察图5(b)还可以发现,当a=10时,含水率在最初阶段存在下降的趋势.这主要是因为kv较小,回灌补充的渗滤液还没有到达探测点,而探测点的残余渗滤液在自身重力作用下发生运移,因此存在含水率下降的趋势.在相同k范围内:当a=2时,SR模型与SU模型达到饱和含水率的时间相同;当a=10时,SR模型与SU模型达到饱和含水率的时间差值为2.3 d.这说明随着a的增加,渗透系数正态分布对于探测点含水率的影响越来越明显.当达到100 d的相对稳定时刻时,SU模型的含水率差值为0.05,而SR模型为0.02.这说明a对于SU模型的影响较大,而对SR模型的影响较小.

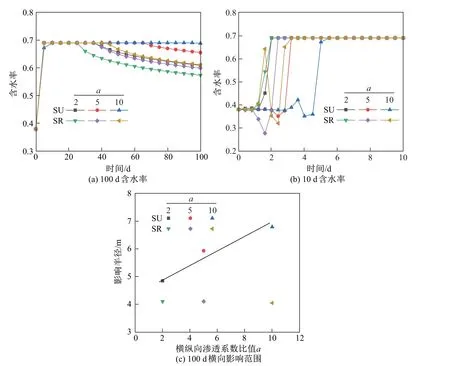
图5 不同a下的含水率分布图和横向影响范围图Fig.5 Water content distribution diagrams and horizontal influence range diagram under different a

由图5(c)可知,随着a的增加,SU模型的横向影响范围呈线性增长趋势,而SR模型则几乎不变,保持在4.09 m.这是由于渗滤液在垃圾体中运移时,优先流过渗透系数较大的地方.SU模型中kh保持不变,而kv逐渐减小,因此渗滤液优先向横向运移,横向影响范围因此逐渐增加.而对于SR模型,渗透系数的正态分布使得kv大于SU模型,a小于SU模型,因此横向影响范围几乎不变.这一现象同时证明了渗透系数的大小和分布方式对于渗滤液的运移起着关键性的作用.

2.3 回灌速率的影响

McCreanor等[11]的实验结果表明回灌速率对渗滤液的运移规律有较大影响.本工作在控制a=2,t=100 h不变,其余参数值如表1所示的基础上,设置q为2、4、6 m3/(d·m)共3个梯度探究其对SU模型和SR模型的含水率以及横向影响范围的影响.

由图6(a)和(b)可以看出,随着q的增加,SR模型和SU模型达到饱和含水率的时间逐渐缩短,SR模型从2 d缩短到0.8 d,而SU模型从2 d缩短到1.6 d.这说明SR模型的kv更大,渗透系数的正态分布随着q的增加影响也越来越明显.在q=6的相同情况下,SR模型优先达到饱和含水率,且持续时间较SU模型稍短,但在含水率下降的情况下,二者的趋势保持一致,说明此时的渗流速度相同.这是由于开始阶段SR模型的kv较大,回灌速率较快,而最终回灌的渗滤液不足以维持该探测点的饱和含水率,且经过饱和状态下渗滤液流动后,该探测点的渗透系数几乎相同,因此最终流速趋于相同.

由图6(c)可知,随着q的增加,SU模型和SR模型的横向影响范围均逐渐增加,二者之间的差值由q=2时的0.7上升到q=6时的0.8,且都呈线性变化趋势.这说明q对SR模型和SU模型有着明显的影响.这主要是由于SR模型的a在不断变化,且kv相比于SU模型较大,因此SR模型的横向影响范围要小于SU模型.而当q越大,SU模型的kv较小时,基质吸附作用更加明显,因此SU模型比SR模型的横向影响范围要更大,差值由0.7增加到0.8.

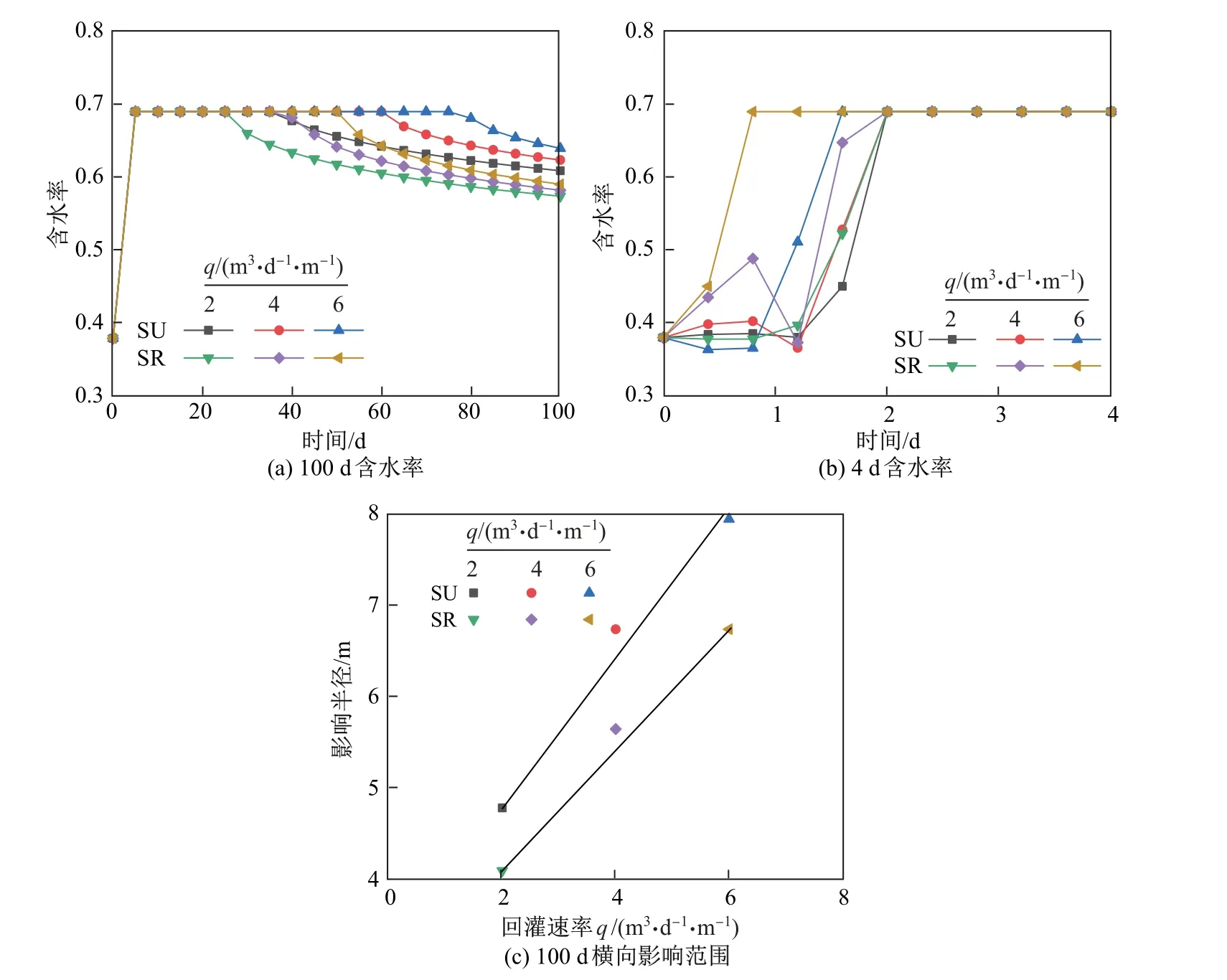
图6 不同q下的含水率分布图和横向影响范围图Fig.6 Water content distribution diagrams and horizontal influence range diagram under different q

2.4 回灌时间的影响

适量的回灌渗滤液能够加速填埋场的降解,而过量的渗滤液则容易导致边坡失稳.在相同的回灌速率下,回灌时间是影响渗滤液回灌量的重要因素,与填埋场的规模有直接关系.本工作在控制a=2,q=4 m3/(d·m)不变,其余参数值如表1所示的基础上,通过设置t=10、60、100 h共3个时间梯度研究了SU模型和SR模型含水率与横向影响范围的变化规律.

通过对比图7(a)和(b)可以看出:随着t从10 h增加到100 h,SR模型在饱和含水率持续时间由3 d增加到25、100 d稳定时,含水率从0.546上升到0.588;SU模型在饱和含水率持续时间由5 d增加到50、100 d稳定时,含水率从0.574上升到0.624.这说明回灌时间t对SU模型含水率的影响更加显著.这主要是由于SU模型的横向和纵向分别是最大和最小渗透系数,渗滤液优先往渗透系数较大的横向运移.而SR模型的横向与纵向渗透系数差值不大,因此含水率变化更加显著.当t=10 h时,SR模型与SU模型稳定在饱和含水率的持续时间相差2 d.当t=100 h时,该值上升到20 d.这表明随着时间t的增加,正态分布对含水率的影响逐渐增加.因此在考虑回灌时间这一影响因素时,需要充分考虑垃圾体的非均质性对其含水率的影响.

图7 不同t下含水率分布图和横向影响范围图Fig.7 Water content distribution diagrams and horizontal influence range diagram under different t

由图7(c)可知,随着时间t的增加,SR模型和SU模型的横向影响范围逐渐增加,且都呈明显的线性增长趋势.SR模型的横向影响范围从1.92 m增加到5.644 m,SU模型从2.206 m增加到6.561 m.当t=10 h时,SU模型与SR模型的差值较小,为0.286.当t=100 h时,SU模型与SR模型的差值为0.917 m,差值逐渐增加.这表明正态分布对横向影响范围的影响随着t的增加越来越趋于明显.这主要是由于随着回灌时间的增加,回灌量逐渐增加,SR模型的kv较大,相同时间内流过的渗滤液量更多;而SU模型的kv较低、孔隙较小,渗滤液优先往孔隙较大的横向运移.因此,SU模型的横向影响范围逐渐增加,且相对于SR模型增加的比例也越来越大.

2.5 模型验证

为了验证本模型的正确性,将其在不同回灌速率下的横向影响范围与McCreanor等[10]的研究结果进行了对比,二者的对比结果如图8所示.设置SR模型下的渗透系数范围为1×10-6～1×10-7m/s,其余参数如表1所示.McCreanor等[10]在均质情况下将渗透系数设置了1×10-5、1×10-6、1×10-7m/s共3个梯度,分别研究了回灌速率在q为2、4、6 m3/(d·m)下的横向影响范围.

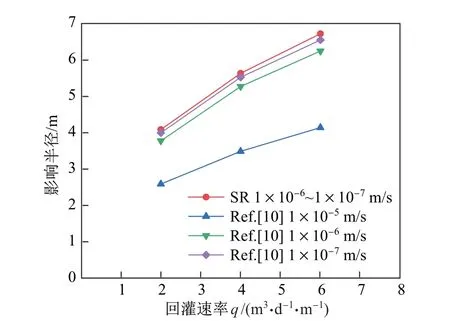
图8 SR模型横向影响范围结果与文献[10]的对比Fig.8 Comparisons between the results of horizontal influence range under the SR model and Ref.[10]

由图8可以看出,使用SR模型得出的横向影响范围预测值与McCreanor等[10]的研究中渗透系数为1×10-6、1×10-7m/s时的整体趋势保持一致.数值上存在略微差别是由于McCreanor等[10]的研究中使用的是均质模型.这说明SR模型能够有效描述垃圾体渗滤液的运移方式,具有一定的合理性和正确性.

3 结论与展望

通过对垃圾体饱和渗透系数随机正态分布的模拟,比较了单孔隙度横纵向均质分布和单孔隙度正态分布在横纵向渗透系数比值、回灌速率和回灌时间等不同因素下,对距回灌井侧向1 m处含水率以及横向影响范围的影响.

(1)横纵向渗透系数比值a对均质分布含水率的影响大于正态分布,且随着a的增加,均质分布的横向影响范围呈线性增长趋势,而正态分布的横向影响范围几乎保持不变.

(2)在相同回灌速率q下,正态分布的渗流速度更快,饱和含水率稳定时间更短,最终达到相对平衡状态时,含水率更小.随着a的增加,均质分布和正态分布的横向影响范围逐渐增加,呈线性变化趋势,且二者的差值逐渐增加.

(3)回灌时间t对均质分布情况下含水率的影响更大.随着t的增加,正态分布对含水率的影响也越来越大.均质分布和正态分布的横向影响范围随着t的增加呈线性增长趋势,且正态分布对横向宽度的影响随着t的增加也越来越明显.

(4)渗透系数是影响含水率和横向影响范围的关键因素,其次是回灌速率,最后是回灌时间.