考虑多种损坏构成特征的沥青路面预防性养护决策方法

李 莉,管婷婷

(上海大学土木工程系,上海 200444)

路面预防性养护是指在不增加路面结构承载力的前提下,对结构完好的路面或附属设施有计划地采取某种具有费用效益的措施,以达到保养路面系统、延缓损坏、保持或改进路面功能状况的目的[1].预防性养护能够以较少的养护投入获得较好的路面性能,在路面寿命期内进行3～4次的预防性养护可以节约45%～50%的养护费用、延长使用寿命10～15年[2].因此,预防性养护理念越来越受重视,但工程中对养护措施如何选择、养护时机如何确定等决策要素尚无统一标准[3].

常见的预防性养护决策方法多为决策树法,即按照路况技术指标分层、分级,逐步匹配适合的预防性养护措施[4-6].路面技术状况指数(pavement quality index,PQI)、路面状况指数(pavement condition index,PCI)等是决策树中较为常用的路况技术指标.然而,由于这类指标综合性较强,由多个要素加权得到,往往难以反映路面实际的损坏特征,用于路面决策时也容易引起偏差[7-9].针对这一问题,一些学者提出在决策树中引入详细的损坏参数,如:Kuhn[10]提出用裂缝、车辙和松散等具体损坏代替综合性指标来描述路面性能;周岚[11]根据江苏省高速公路的实际损坏状况,提出了路面破损的横向裂缝指标、修补率和表面破损状况等指标;刘胜强[12]提出在综合性路况指标的基础上增加了百米当量横缝条数、块状修补率和车辙率.这些细观指标的引入在一定程度上提高了路面预防性养护决策的准确度,但也令决策过程更为复杂,因为细观指标的选取和使用方式往往依赖于当地的路况特征,难以在不同区域的道路上移植,不利于标准化.

因此,有必要对综合性路况指标进行深入分析,明确其容易引起预防性养护决策偏差的深层次原因,并研究针对性的决策改进方法.本工作将以工程应用中使用较多的PCI指标为代表进行分析.

1 不同PCI水平下损坏特点分析

PCI综合考虑了多种路面损坏的情形,如线裂、网裂、坑槽、车辙等[13],其中损坏最严重(扣分最多)的称作“主导损坏”.在预防性养护决策中通常需要同时考虑PCI水平和路段“主导损坏”,以选取最具针对性的养护措施[14].然而,这种决策方式有效的前提之一是“主导损坏”能够真正代表路面的损坏特征.因此,首先需要对不同PCI水平下的路面损坏构成进行分析,量化“主导损坏”的代表性.

1.1 基于PCI评分的路段分组

按照PCI评分将路段分组,可分离不同的路面损坏发展阶段,从而分别研究各阶段的损坏构成特点.按照现行规范对PCI分级(优、良、合格、不合格)是最直接的分组方法[1],但该方法仅考虑了PCI评分,而忽略了PCI评分和损坏分布的关系,故分组结果未必最优.因此,有必要同时考虑PCI评分和路面损坏分布,利用数据自身的内聚特征进行分组.实现这一目的的算法有多种,如变尺度混沌优化算法[15]、人工蜂群算法[16]和有序聚类算法[17]等.有序聚类算法适合处理大量数据,能够同时找到多个最优的插入点将有序序列划分为多组,在多个领域得到了成功应用[18-19].因此,本工作采用有序聚类算法对路段进行分组,要求组内PCI尽可能接近,而组间PCI差异尽可能大.

1.1.1 有序聚类算法

1958年,Fisher[20]提出了最优分割法.1982年,方开泰[21]对最优分割法做出一些改进,提出了一维和二维数据的有序聚类方法.2011年,Liu等[22]针对有序聚类算法运算时间过长的问题做出了改进,提出当数据序列不满足修剪条件时,通过添加余弦相似度比较来减少计算时间.此后,有序聚类法得到了广泛应用[18,23].

有序聚类算法的思想是寻找最优分割点,使分组后产生的离差平方和的增量最小,从而实现组内尽可能保持均质性、而组间对比鲜明[24].

(1)计算各组直径.

设有序样本x1,x2,···,xn,其中xi为第i个样本的特征值.记有序样本中某一分组为Gij={xi,xi+1,···,xj}(j＞i),该分组的平均值为,直径为D(i,j),则有

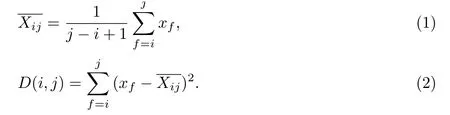
(2)定义误差函数.

将n个有序样本分为k组,记为p(n,k),则有

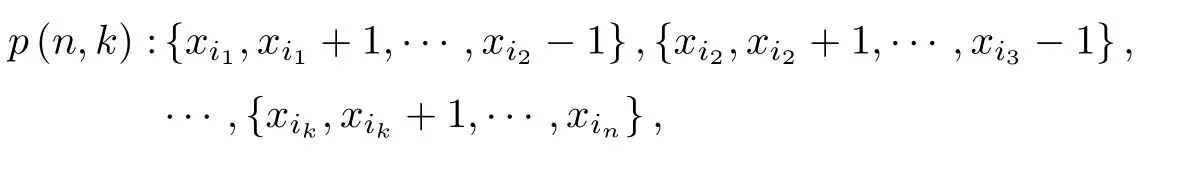
简记为

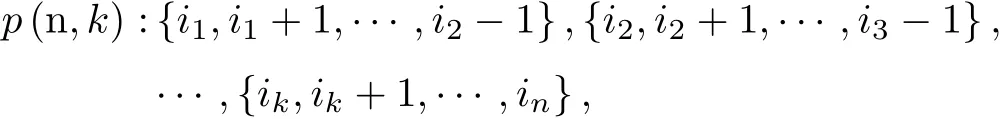
式中:1=i1＜i2＜···＜ik＜in=n.

定义p(n,k)的误差函数为

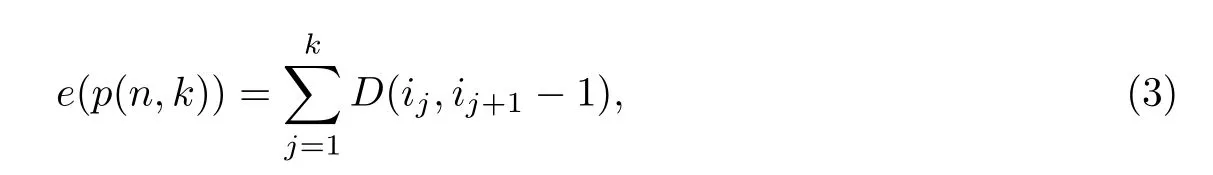
当n、k确定时,e(p(n,k))越小表示段内离差平方和越小,分组越趋于合理.因此,目标为寻找令e(p(n,k))达到最小时的分组.

(3)精确最优解的求法.

求解过程从计算j2开始,一直计算出jk为止,具体算法如下:

当k=2时,

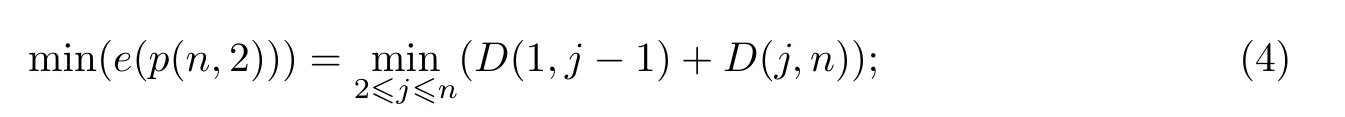
当2＜k≤n时,

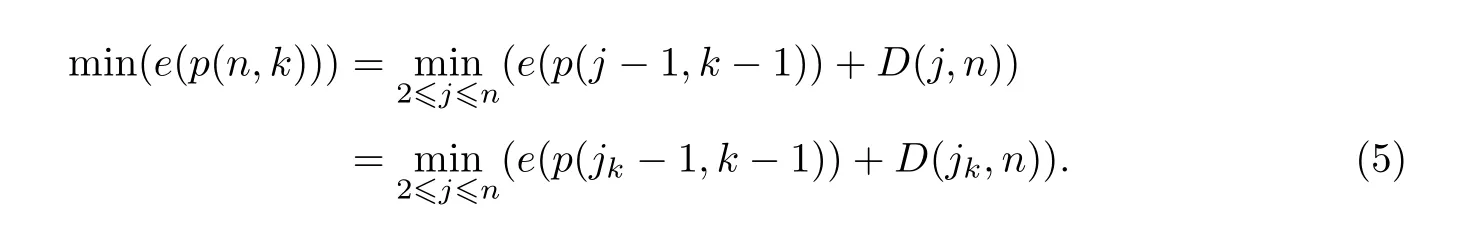
要找到j=jk使得式(3)～(7)取最小值,得到Gk={jk,jk+1,···,n}.

对于任意的j必须使前面的j-1个样本最优分割为k-1组,且式(6)成立,得到Gk-1={jk-1,jk-1+1,···,jk-1}.

类似地,可以得到G1,G2,···,Gk,即所求的最优分组.

1.1.2 实测数据分析

本工作以城市道路数据为例进行分析,收集了2015—2019年上海市城市道路沥青路面性能数据共计11 250条,包括路面等级、长度、宽度、基层面层厚度、路龄等基础信息,各种路面损坏(如线裂、网裂、坑槽等)的检测信息,以及PCI、RQI、结构强度等计算结果.将路段按照PCI评分排序,并将PCI评分作为有序聚类的特征量,按照有序聚类算法对11 250个路段进行分组.

图1为分组数与最小误差函数值的关系.可以看出:随着分组数的下降,误差函数值不断减小;但当分组过多时,组间的数据就相对较少,失去了分组的意义;当分类数k=10时,误差函数下降速度下降最快,曲线出现明显拐点.因此,结合实际PCI的分布情况,本工作将路段分为10组,结果如表1所示.

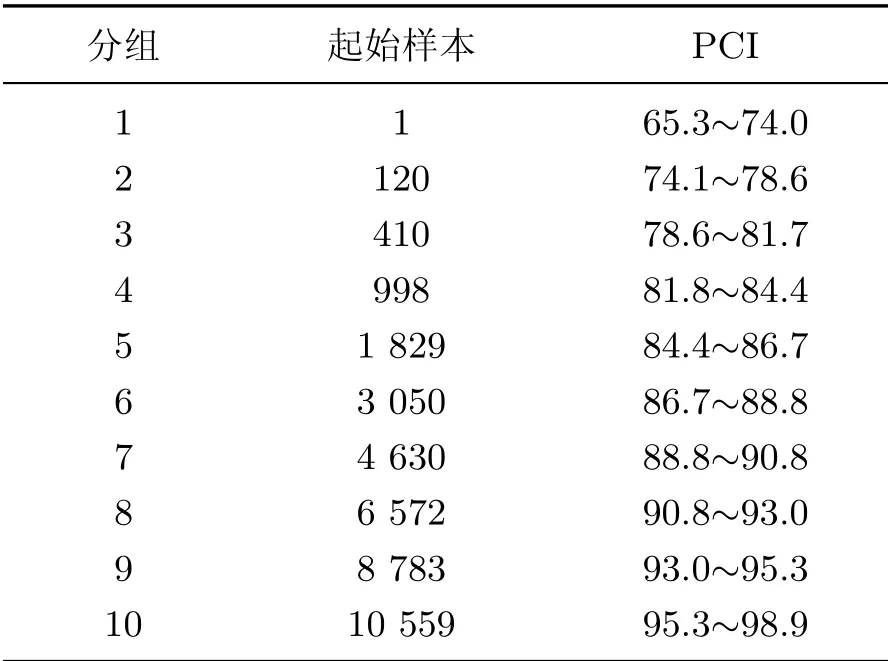
表1 路段数据分组Table 1 Grouping result of section data

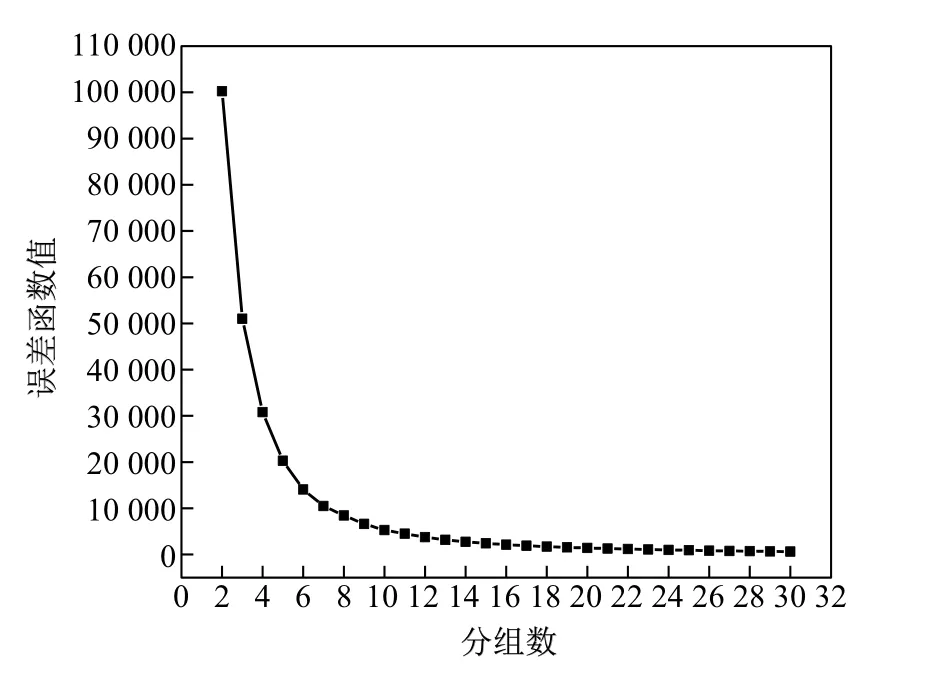
图1 分组数与最小误差函数关系Fig.1 Relationship between number of groups and the values of minimum error function

1.2 损坏特点分析

基于上述分组,分析不同PCI水平下的路面损坏分布特点.当路段存在多种损坏且损坏程度差异不大时,主导损坏可能失去代表性.因此,首先需要分析PCI水平和损坏种类数量的关系,其次需要明确多种损坏并存时,不同损坏之间的差异程度.

实测路段数据中共包含了9种损坏形式.PCI和损坏种类数的关系见表2.可以看出:当PCI较高时,绝大多数路段只有一种损坏(如分组10);随着PCI的下降,存在多种损坏的路段数逐渐增多,且分布越来越分散;当PCI低于90.8分时(分组1～7),95%以上的路段超过2种损坏.由此可见,大部分路段的损坏形式并不单一,还需进一步分析各损坏的差异程度.

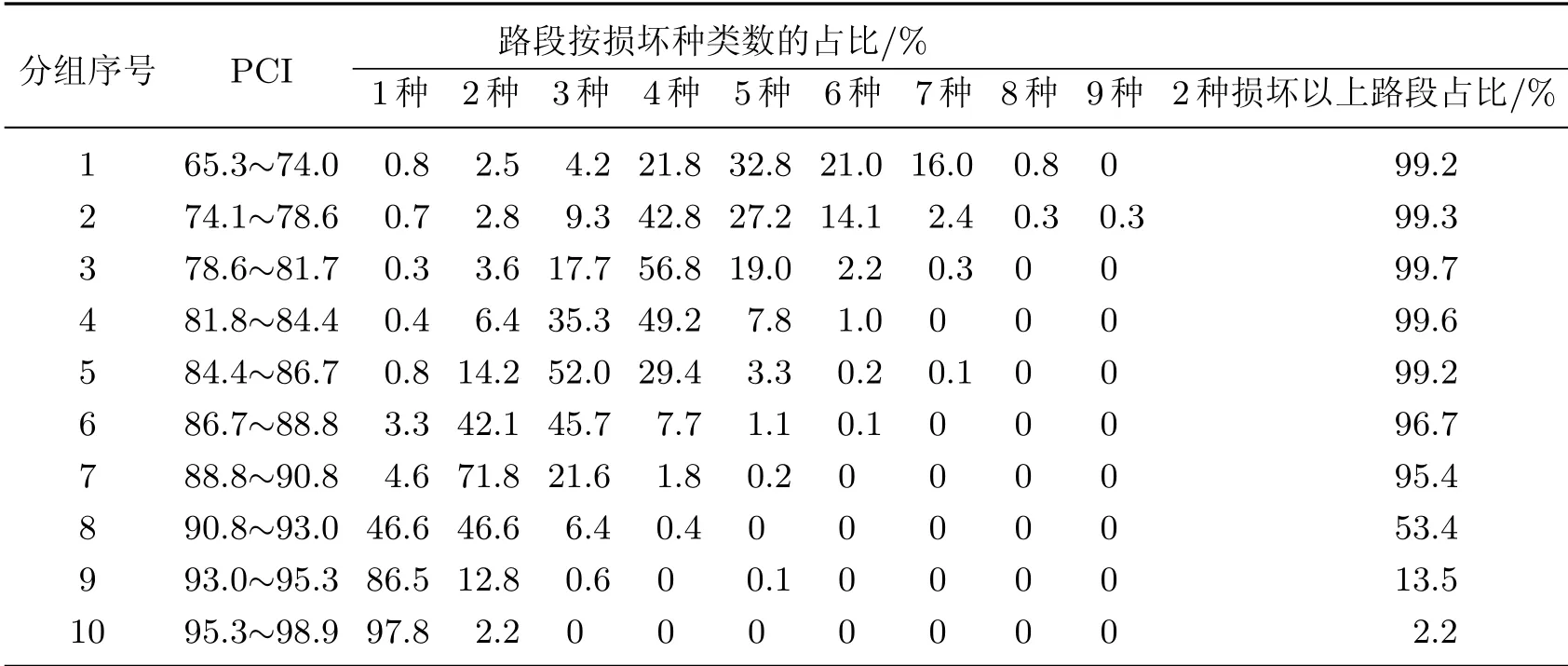
表2 各组路段按损坏种类数的统计结果Table 2 Statistical results of each section group according to the number of damage types

对存在2种及以上损坏的路段,进一步量化不同损坏的差异程度.PCI计算模型中的单项扣分值是根据损坏类型、密度、程度给出,从而使得不同的损坏具有可比性[1].因此本工作采用单项扣分值表征各种损坏的严重程度,变异系数Cv表征不同损坏扣分值的差异程度,

式中:σ为各损坏单项扣分值的标准差;μ为各损坏单项扣分平均值.

图2所示为各分组路段损坏差异的分析结果.可以看出:当PCI水平较高时,变异系数Cv较大,表明各损坏严重程度的差异较大,主导损坏较为突出;随着PCI水平的下降,变异系数Cv不断减小,表明损坏间的差异减小,各损坏的影响程度趋同;当PCI水平继续降低(低于86.7分)时,变异系数Cv再次逐步上升,表明不同损坏的差异逐渐增大,主导损坏的影响再次突出.总之,当PCI为84.4～93.0分时,不同损坏的差异尤为不明显,即主导损坏并不能概况路面实际损坏特征,而这个PCI评分范围恰是通常认为适合预防性养护的范围.这也间接证明了仅利用PCI这类综合性路况指标和主导损坏指导预防性养护决策可能并不准确.对多种损坏同时存在且差异较小的路段,应考虑更具区分度的决策方法.

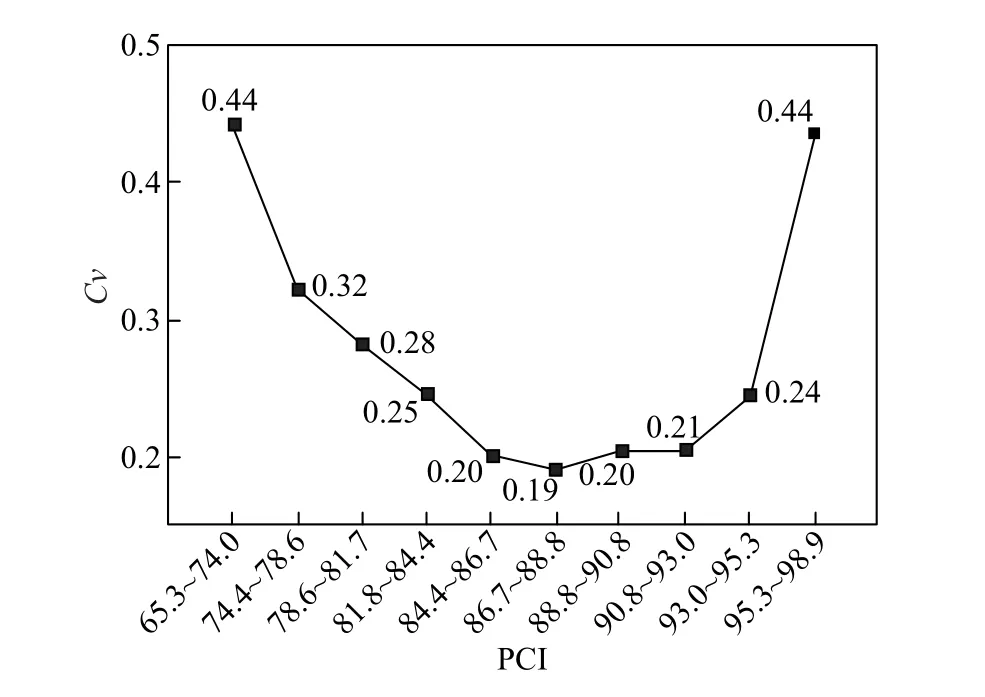
图2 各组损坏扣分变异系数图Fig.2 Variation coefficient of damage deduction for each group

2 基于损坏分布的BP神经网络建模

除了利用路况评价数据外,经验丰富的决策者一般会在实地踏勘的基础上根据路面具体损坏情况给出预防性养护建议.经验知识在解决复杂的养护决策问题时往往具有重要作用[25].传统的决策树和专家系统可根据经验知识来推理、判断,模拟资深专家的思维过程,利用经验知识指导解决实际的决策问题[26].但当输入变量增加时,多种指标的组合数呈指数级增长,经验知识难以通过决策树和专家系统准确表达.此外,当调整决策参数时,需重新定义规则,较为耗时耗力[27].相比而言,神经网络方法在经验知识模型化方面具备显著优势,不仅能够模拟参数之间复杂、模糊的因果关系,还能够根据数据变动自动学习规则、调整网络结构.神经网络在路面养护领域也已经大量应用,例如:沙爱民等[28]利用神经网络实现了路基病害的高效识别;陈仕周等[29]将BP神经网络用于沥青路面使用性能的预测,取得了较高的预测精度;Domitrovi´c等[30]利用神经网络建立路面养护决策模型,成功利用了工程实际中积累的养护经验知识.

BP神经网络能够通过输入、输出的数据不断调整内部结构参数,从而自动创建知识系统,属于有监督的学习方法[31].本工作采用BP神经网络方法对PCI水平接近、多种损坏并存且差异不大的路段进行预防性养护决策.BP神经网络方法有效的前提是能够利用反映正确预防性养护经验的数据进行模型训练,因此,首先需要筛选具备正确养护经验的路段.

2.1 有效养护路段筛选

“有效养护”定义为进行预防性养护后,路段的PCI评分有所提高.按照此标准,对PCI处于84.4～93.0分的路段进行筛选.首先,筛选出进行过预防性养护的路段,再分析路段在预防性养护前后的路况检测数据,筛选出ΔPCI＞0的路段,作为具备正确养护经验的路段.

式中:PCI1为路面养护后的PCI评分;PCI2为路面养护前的PCI评分.本工作共筛选出符合条件的路段431个,其检测数据、养护数据将用于BP神经网络建模.

2.2 模型参数分析

工程实践中,预防性养护措施的选择主要考虑路面技术状况、道路交通等级、面层厚度等因素[5].现行的预防性养护决策是以路面结构强度指数(structure strength index,SSI)足够、横向力系数(sideway force coefficient,SFC)优良为前提,而本工作的决策方法是在此基础上进行的补充,因此结构强度和路面抗滑不再作为补充方法的影响因素.路面行驶质量、路面损坏状况都对预防性养护对策的选择影响较大,因此将路面行驶质量指数(riding quality index,RQI)、PCI作为养护对策的影响因素.为了比较具体损坏构成对养护决策的影响,本工作建立了两个BP神经网络模型,二者的主要区别在于对路面损坏状况的表征方式不同.模型1为PCI和主导损坏,模型2为PCI和全体损坏.除此之外,面层厚度、交通荷载等路段基础数据也会影响预防性养护决策,故也将其作为建模参数.对于模型训练的预防性养护措施,本工作收集了相应路段2015—2019年的养护记录,由于是以城市道路为例,预防性养护措施种类相对较少,故分为灌缝、罩面、微表处3类.表3和4为BP神经网络建模所用的参数.

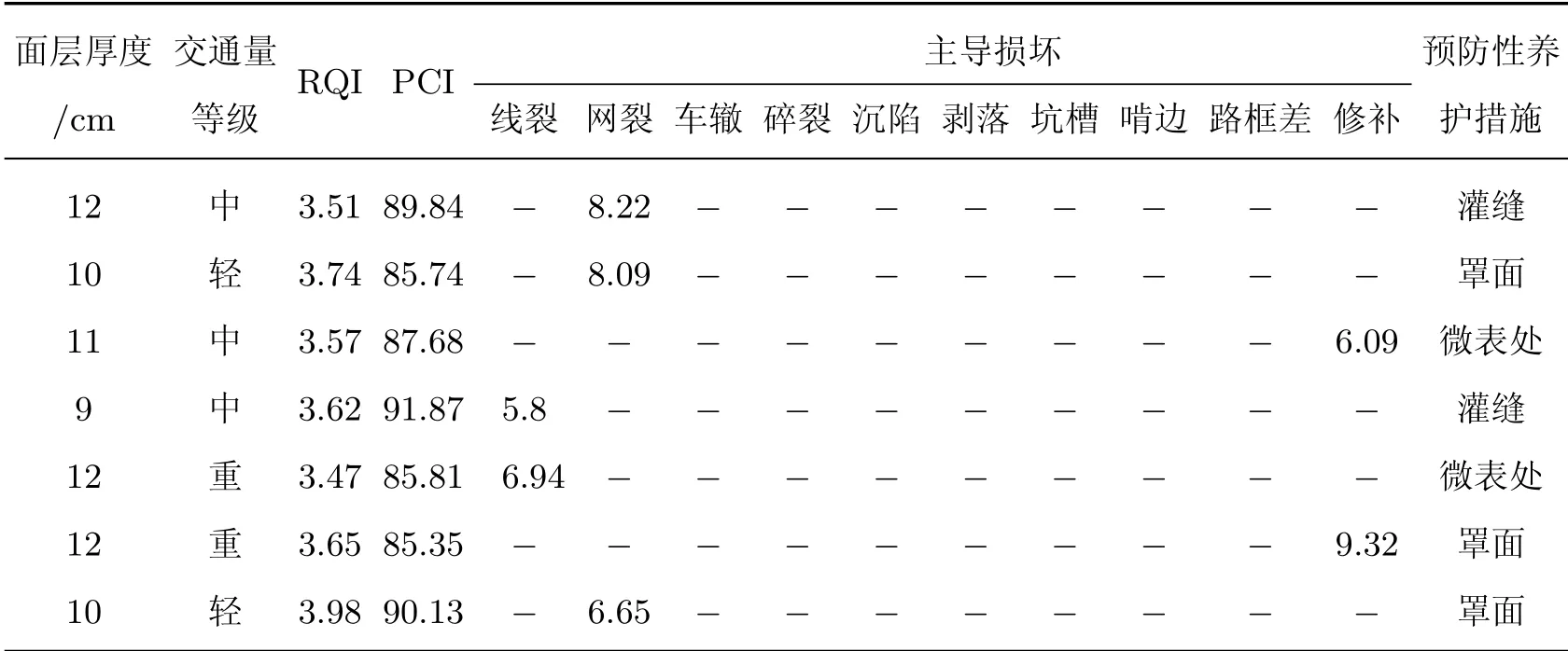
表3 BP神经网络模型1训练参数实例Table 3 The example of training parameters of BP neural network for Model 1

表4 BP神经网络模型2训练参数实例Table 4 The example of training parameters of BP neural network for Model 2

2.3 BP神经网络建模

Kolmogorov定理证明了BP神经网络具有强大的非线性映射能力和泛化能力,任一连续函数或映射函数均可采用3层网络加以实现[32],因此本工作采用3层(输入层、隐含层、输出层)BP神经网络建立两个模型.模型1和模型2的输入层神经元均为14个,输出层神经元均为3个(见表3和4).隐含层的神经元数量一般没有统一标准,但数量过少时易发生欠拟合,难以恰当表达输入和输出的关系,数量过多时又易出现过拟合,弱化模型的泛化能力,因此一般由经验公式确定隐含层神经元数量[33].

式中:N为隐含层神经元数量;m为输入神经元数量;n为输出神经元数量;a为1～10的常数.按照式(9),得到隐含层的数量为5～14个.本工作经反复调试,将隐含层神经元数量定为14个,得到的结果更加稳定(见图3).

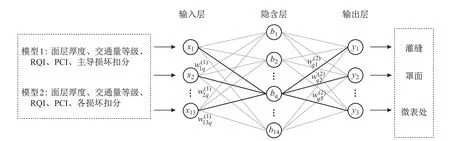
图3 BP神经网络模型结构图Fig.3 The structure diagram of BP neural network model

BP神经网络训练模型实际是优化误差函数的过程,反复训练迭代直至找到全局最优的权值和阈值[34].本工作采用Trainsag共轭梯度算法来调整全局权值和阈值,这是因为相比于其他算法,该算法的搜索方向是负梯度方向和上一次迭代搜索方向的组合,不需要矩阵储存,具有较快的收敛速率[35].

将431个养护效果良好的路段数据随机分为3份,其中训练集占70%,验证集和验证集各占15%.训练集用于计算梯度、更新权重和阈值;验证集用于确定最优迭代次数;测试集用于评估模型的泛化能力,即训练好的模型对新样本的判别、推广的能力.

2.4 结果分析

2.4.1 训练速度

当训练集误差降低而验证集误差升高时,停止训练,将此时对应的迭代次数作为最优迭代次数,可在一定程度上缓解过拟合的问题[36].图4为BP神经网络训练误差曲线.可以看出:随着迭代次数的增加,输出结果的误差迅速减小;模型1迭代34次时达到最优,交叉熵为0.28;模型2迭代72次时达到最优,交叉熵为0.14.因此,从收敛速度来说,模型1更优.

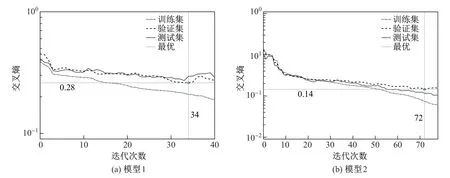
图4 BP神经网络训练误差曲线Fig.4 Training error curve of BP neural network

2.4.2 匹配精度

图5为模型1和模型2对各类养护措施匹配精度用混淆矩阵表示,其中对角线内数字表示分类正确的路段数及比例,对角线外为误分类.

图5 训练集混淆矩阵的Fig.5 Training confusion matrix

模型1对灌缝、罩面、微表处的匹配准确率分别为89.7%、75.6%、44.6%.对罩面和微表处的匹配精度较低,表明根据主导损坏难以确定选择罩面还是微表处.而模型2对灌缝、罩面、微表处的匹配准确率可达92.7%、86.8%、86.4%,较模型1有了明显提高,表明基于完整的损坏构成更容易得到针对性的养护措施.模型2的总体匹配精度可达89.7%,较模型1(77.1%)提高了16%.因此模型2的匹配精度更高,基于详细损坏分布选择的养护措施表现出的规律性更强,更符合预防性养护工程实际.

2.4.3 泛化能力

图6为两模型对训练集、验证集和测试集的准确率.可以看出,模型2测试集的匹配准确率为86.2%,较模型1(58.5%)明显提高.因此,模型2的泛化能力较强,对新样本的判别能力更强.模型2训练集、验证集和测试集的匹配精度变化幅度较小,说明模型2在3种数据集上的表现差异不大,得到的结果更加稳定;而模型1在不同数据集上的表现差异较大,测试集和训练集的匹配精度难以维持在相似的水平.因此,相比于主导损坏,基于详细损坏分布的养护决策模型的性能更加稳定,更适合用于指导路面预防性养护.

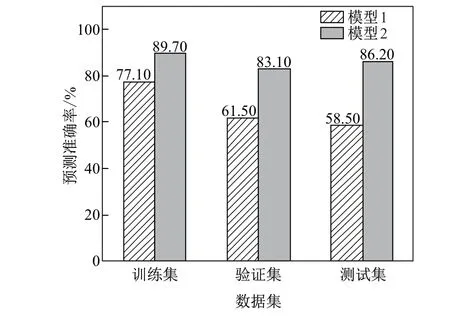
图6 模型1和模型2的准确率Fig.6 Decision accuracy of model 1 and 2

3 模型应用

基于以上分析,PCI处于优良之间(84.4～93.0分)的某一分段时,主导损坏可能无法概况路面损坏特征,采用传统的决策树法进行预防性养护对策选择可能难以取得良好效果,因此可在决策树法的基础上加以改进,引入模型2所示的BP神经网络.当路段满足预防性养护条件且PCI介于该分段时,将各损坏的单项扣分值、PCI、RQI等数据代入神经网络,即可得到更具有针对性的预防性养护参考意见,其决策流程如图7所示.随着路面历年检测数据的积累,上述损坏构成差异较小的PCI分段会更逐渐稳定.同时,随着养护数据的累积,神经网络也可通过不断的迭代、学习,将积累的正确有效的养护经验不断反馈到养护决策中,为复杂的路面养护决策问题提供一种高效、优化的解决方案.

图7 预防性养护补充决策方法Fig.7 Supplementary method of preventive maintenance decision

4 结束语

本研究针对综合指标和主导损坏对路面损坏特征表征不够全面的问题,在传统预防性养护决策树方法的基础上,提出了基于BP神经网络的改进方法,对主导损坏不突出的路段补充了针对性的决策方法.

(1)针对本研究中使用的数据,当PCI低于90.8分时(分组1～7),95%以上的路段有2～9种损坏;多种损坏的差异随着PCI的降低先减小后增大;当PCI处于84.4～93.0分时,不同损坏的差异尤为不明显,主导损坏难以表征路面实际损坏特征.

(2)基于有效养护路段和BP神经网络,考虑不同的损坏构成,分别建立并比较了2个预防性养护决策模型.模型2训练集的匹配准确率更高;模型2的泛化能力更强,测试集的匹配准确率达到了86.2%.因此,相比于主导损坏,基于多种损坏构成的养护决策模型精度更高、泛化能力更强且更稳定.

(3)BP神经网络与传统决策树法结合能够优化沥青路面预防性养护决策过程,提高养护对策选取的针对性,更符合实际的预防性养护决策,更适合推广用于指导路面预防性养护.