完形修复:指向数学素养的核心区域
江苏淮安市实验小学(223002) 薛仕扣
一、完形修复,人的一种基本认知活动方式
1.相映成趣的心理实验
如图1,如果遮住A 和C,我们会不约而同地认为图中有三个数,依次是12、13、14;如果遮住12 和14,同样我们会认为图中有三个字母,依次是A、B、C。对于中间的部分,放在不同的情境中竟然会出现不同的答案(13或B),然而这就是人之常情!

图1
2.人之常情的背后思考
人在认识事物时,首先映入大脑中的是事物的整体,而不是事物的各个组成部分,这个整体即为完形。图1 中12、13、14 或A、B、C 组成的整体就是不同的完形。
3.俯拾即是的完形修复
人在面对一种不完美的刺激物时,会在认知中情不自禁地产生一种急于要使之完满的趋向,从而倾向于建立一个完形整体,这一过程即为完形修复。例如,图2 是独立的三个扇形,但通常情况下,人的认知倾向于它是一个三角形(自觉弥补三角形边上的缺失部分),而忽视了其为独立的三个扇形。这个修复过程是个体主动的,且修复完成后将难以改变。

图2
二、完形修复,指向数学素养的核心区域
1.意义剖析,感受完形修复的价值性
(1)在元素与整体中辨析
完形之“形”不是外物的形状,也不是一种形式,而是知觉中的“形”。完形心理学认为,心理现象最基本的特征是意识经验中显现出来的整体性和结构性,整体性既包括构成它的部分,又包括产生于独立其组成要素的全新整体。元素论主张对事物进行解剖研究,把元素从整体中割裂出来,研究其属性,并把整体的特征简单归结为元素之和。F.克莱因认为,数学教师应使学生了解数学知识并不是孤立的各部分,而是一个有机的整体。教学中,教师要注重数学的不同分支和不同内容之间的联系,数学与日常生活的联系以及数学与其他学科的联系。
(2)在自然与数学中共鸣
完形心理学认为,人的大脑中先天存在着一些力的结构样式,当物理中的力的样式与心理上的力的样式相对应时,外在对象和内在情感便产生共鸣,外在对象便具有了情感表现性,人就会产生审美体验。自然美与数学美是相互呼应的,在数学世界里,鹦鹉螺线、对数螺线、黄金分割、斐波那契数列等都蕴含着数学的美妙与神奇。
(3)在张力与平衡中调和
张力与平衡是一对互相矛盾又互相补充的认知规律。平衡是富有张力的动态平衡,张力是在一个平衡的样式中呈现的富有倾向性的张力。数学课堂教学要凸显力的冲突,制造学生心理上的认知失衡。数学学习的内容应该是现实的、富有挑战性的。比如,教学“面积和面积单位”一课,在学生难以用重叠法比较两个不同长方形的大小时,便产生认知张力,进而思考“如何使用间接方法比较或用哪种图形作面积单位最合适”,通过问题引发认知冲突,进而引出面积单位。
2.追根溯源,寻找完形修复的“存在感”
(1)在同化和顺应的过程中修复完形
建构主义理论认为,人的知识获取存在着两种不同的方式,即同化和顺应。以顺应方式进行学习的原因是人的已有知识经验匮乏,需要通过顺应不断建立新的知识系统。在此过程中,顺应的过程从某种层面上讲就是个体修复的过程,即建立新的知识系统这一新的完形。
例如,在教学“圆锥的体积”时,部分教师会让学生先拿两个等底等高的圆柱和圆锥容器,然后用圆锥容器装满水倒进圆柱容器里,发现倒3 次后圆柱容器里的水正好满了,进而得出圆锥和圆柱体积的关系。这样的活动,看似是学生通过动手操作探究圆锥的体积,实质上是在教师的指令下完成的,学生未能积极主动地参与到知识顺应的过程中,只是被动学习。为此,笔者进行了调整,课前准备大小不等的圆柱和圆锥(其中有等底等高的圆柱和圆锥)容器,让学生自主选择后进行小组合作探究,最后师生共同得出结论。通过小小的调整,教师的指令没有了,学生真正通过自主合作探究,最终得出圆锥的体积计算方法。
随着知识经验的不断积累,当遇到新知时,人们更倾向于从旧知中寻找与新知的关联度,一旦找寻到,人们就会自觉将新知纳入原有的知识系统中,形成新的知识体系,最终建立更为完善的新的完形体系。这一同化的过程即为人自觉主动的修复过程。例如,当学生认识了长方形后,教师出示1 个长方形并提问“这是什么”,学生会回答“是长方形”,而不会回答“是4 条线段”。可见,长方形是学生自主修复所建立的新完形。同理,当学生认识长方体后,教师出示1 个长方体并提问“这是什么”,学生会回答“是长方体”,而不会回答“是6 个长方形”。
(2)在整体和系统的结构中修复完形
把知识整体、系统地呈现给学生,学生在旧知的基础上,把零散的知识按层次连接为系统结构体系。在连接的过程中,零散的知识不可能清晰地出现在结构体系中,很多时候是模糊的、有缺陷的,这给学生进行自主修复提供了可能。学生不仅要认识事物的外部特征,还要理解其隐含的本质规律;不仅要知晓个别零散的知识,还要把握知识之间的联系,由此构成由表及里、由此及彼的完形知识结构。
例如,在教学“分数的基本性质”时,当学生得出“分数的分子和分母同时乘或除以一个相同的数,分数的大小不变”的结论后,笔者略作停顿。不一会儿,一位学生举起了手,说:“同时乘或除以的数不能是0。”笔者因势利导,问:“为什么不能是0?”这位学生回答:“因为分母不能为0,如果分子和分母都乘或除以0,所得分母就是0。”
当学生总结概括出分数的基本性质(不完整的)后,笔者没有立即评价,也没有问学生“可不可以同时乘或除以0”,而是略作停顿,给学生提供了修复的时间和空间,让学生自主修复分数基本性质的完形。这种教学方式不仅有利于学生头脑中新旧知识的结合,而且还能激发学生的认知潜力,进一步培养学生用深入、联系的思维方式去认识周围事物。
(3)在留白和想象的地带中修复完形
首先,巧设板书,为学生完形修复搭建“脚手架”。
随着科技的发展,许多现代化的教学手段走进课堂,但是板书在教学中仍然起着不可替代的作用。板书是体现教材思路、教师教路、学生学路的最佳形式,一次好的板书能简练、系统地体现教学内容,以明晰的视觉符号启迪学生思维,给学生提供记忆的框架结构。
例如,在旁听“笔算两位数加两位数(进位加)”时,图3是执教教师设计的板书,图4是笔者在执教教师的基础上略加修改形成的板书。

图3

图4
图3 的板书直接告知学生笔算两位数加两位数(进位加)的步骤,图4 的板书则出现了一些空白,正是因为这些空白的存在,激起学生对笔算两位数加两位数(进位加)这一完形进行自主修复的欲望。
师生对话是课堂教学中最常用也是最主要的一种手段。对话不是简单的“教师问、学生答”,更不是“教师讲、学生听”,而是通过对话启迪、唤醒学生主动思考。在对话的过程中只有给学生提供完形修复的场域,才能启动学生思维的翅膀。
其次,杜绝啰唆,为学生完形修复营造“自组织”。
课堂教学是一门艺术,而课堂教学中的师生对话更是一门高级艺术。课堂上,教师的啰唆主要表现在三个方面:第一是无意识的口头禅,如“啊”“嗯”“哦”“这个”等;第二是意思相同的提问,如一个问题提出后,在学生还没有回答或者回答不出来时,又接二连三地换角度重复提同一个问题;第三是重复学生的答案,如学生回答后又重复学生的答案后才进行现场评价。久而久之,教师的这些啰唆会干扰学生进行自我修复。
教师应将课堂视为实现完形的阵地,充分调动可用资源,提供灵动“对话场”、营造积极“自组织”、激活融通的“心物场”和搭建最佳“脚手架”,以激发学生的完形意识,建立良性的“同构”关系,促成学生自觉能动地进行完形修复。学生在改造、补充完形的过程中,容易激起大脑的潜力,提高认知的兴奋程度,从而引起一种进取的、充满紧张感的内驱力。在这种内驱力的驱动下,学生会积极主动地去“填补”不完美的刺激物。
3.同课异景,让完形修复提升学生数学素养
例如,在教学“平行四边形的面积”时,笔者首先带领学生复习长方形面积的计算方法,接着问学生如何求平行四边形的面积。学生猜测用相邻两条边相乘,笔者否定了学生的答案,但没有告诉学生为什么否定,而是直接演示将平行四边形转化成长方形的过程(如图5)。在笔者的引导下,学生根据转化前后的关系,得出“平行四边形的面积=底×高”。

图5
上述教学中,学生真的掌握了求平行四边形面积的计算方法了吗?为求验证,笔者出示图6 并提问:“如何计算这个平行四边形的面积?”学生异口同声地回答:“10×15=150(cm²)。”笔者对学生的回答表示肯定,接着追问:“你们是怎么算的呢?”学生按照之前的方法画出了图7,可是画完后发现与之前学的(图5)不一样,学生陷入了思考。
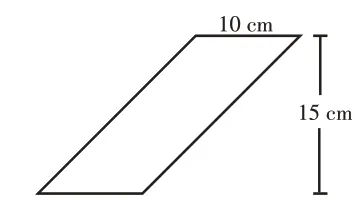
图6

图7
通过学生异口同声的回答可以发现,学生看似建立了平行四边形面积计算方法这一完形,但对图6 这种平行四边形,无法用之前的经验转化成长方形,说明这一完形是有缺陷的。学生陷入思考的过程是一种自觉完形修复的过程。
接着,笔者没有任何干涉,学生进行自主探索。有的学生从平行四边形上面切取一个直角三角形移到下面,转化成长方形(如图8);有的学生先将作业本旋转90°,再割补图形,最后转化成长方形(如图9)。

图8

图9
在仔细观察图形的基础上,如何把平行四边形转化成一个面积与之相等的长方形,围绕这样的中心问题,学生自觉对已建立的完形进行修复,最终豁然开朗。
三、理性把握完形修复过程中存在的问题
学生的学习过程不应只有教师的指导,还应有一种自觉的重新组织。学生的学习过程是在组织构造一种完形,并对其中各种关系进行认识,这种完形过程一旦建立,将会形成学生自动化的行为方式。
在教学过程中,如果教师制造的“陷阱”太少,学生不假思索就能轻易获得完形,缺少了修复的过程,但如果教师制造的“陷阱”太多,学生会因捉摸不透而无法修复。因此,在完形修复的过程中,教师需要把握一定的尺度,这样才能发挥应有的作用。
1.完形消逝,对学生修复的过程过度关照
课堂上,有的教师生怕学生听不懂,总是讲得太多且从不制造“陷阱”,或者制造“陷阱”自己跳,不敢让学生去跳,忽视了学生对所学内容的修复过程。一节课下来,教师口干舌燥,学生只是被动接受,如此,因缺少修复的过程导致完形消逝。
2.完形失败,对学生修复的过程放任自流
课堂上,有的教师对学生的想法缺乏恰当的引导,造成学生对所学内容完形失败。
例如,在旁听“倒数的意义”时,执教教师这样导入:“同学们,在日常生活中,很多东西可以倒置。比如,书可以倒放、杯子可以倒放(杯口朝下)……今天我们一起来学习倒数,猜猜看,倒数是什么?”学生的回答五花八门,有的说倒数就是将数倒过来,如1 倒过来是1,8 倒过来是8,6 倒过来就变成9;有的说倒数就是倒着数数……学生的回答与倒数的意义没有任何关系,最终导致学生对“倒数”这一概念完形失败。
“要使不同的人在数学上得到不同的发展。”在数学教学中,学生对某一学习内容的完形修复是存在差异性的,不能一概而论。教师要针对学生的不同特点,从多种角度发掘学生的潜能,用积极的心态去认识学生完形修复的过程,遵照不同学生完形修复的差异性。

