深度学习在ARX 分组密码差分分析的应用*

杨小雪, 陈 杰,, 韩立东

1. 西安电子科技大学 通信工程学院, 西安 710071

2. 杭州师范大学 浙江省密码技术重点实验室, 杭州 311121

1 引言

神经网络是实现深度学习的主要方式, 而深度学习属于机器学习的一个分支, 它利用算法来处理数据、提取特征、模拟人类思维或者进行开发. 深度学习的历史可以追溯到1943 年, 当时Walter Pitts 和Warren McCulloch 创建了一个基于人脑神经网络的计算机模型. 随着计算机处理数据速度的加快, 如今深度学习在很多领域都有广泛的应用[1–4], 比如图像识别、自动驾驶、AI 机器人等.

1991 年, Ronald Rivest 首次将深度学习和密码分析联系起来, 在文献[5] 中提出了关于密码学和机器学习两个领域的主题调查. 然而, 由于早期计算机硬件的运算能力有限, 深度学习的发展受到限制, 因此它在密码学领域的应用成果并不多, 主要集中在侧信道攻击[6,7]上. 但侧信道攻击属于物理攻击, 并不属于真正意义上的密码分析. 此后, 随着GPU (图形处理单元) 技术的不断发展和深度学习一些新算法的提出, 机器学习在密码分析上的应用越来越广泛. 2008 年, Bafghi 等人利用蚁群算法开发了一个模型,将Sperpent 分组密码差分特征空间用一个加权有向图表示, 再利用递归神经网络找到其中的最小权重多分支路径, 从而得到最佳差分路径[8]. 2009 年, Soos 等人将SAT 求解器引入到密码问题中[9], 并取得显著效果. 自此, 自动搜索技术得到广泛应用, 在发现分组密码特征上比机器学习更有优势. 由于机器学习在发现分组密码特征上的竞争力不够, 学者们开始关注其他方面的应用, 比如利用机器学习算法来对加密流量和密码算法进行分类. 2015 年, 文献[10] 使用了三种基于机器学习的分类方法来对加密数据进行分类, 均在实际药物数据集上运行时有效地执行分类. 2017 年, Liu 等人提出利用无监督学习来对无标记数据进行分类, 并展示了如何应用该方法来分析Caesar 密码[11]. 2018 年, De Mello 等人利用六种学习算法识别在EBC 和CBC 工作模式下的七种加密算法[12], 在EBC 模式下的识别成功率非常高, 在有些算法下甚至收敛到100%. 原本CBC 模式对区分攻击不敏感, 而在文献[12] 中, 在CBC 模式下成功识别密码算法的范围为40—50%. 然而以上工作都没有对现代密码算法进行实际的攻击和破解, 因此学者们开始进行一些新的研究, 他们利用机器学习寻找明文、密文和密钥的映射关系. 2018 年, Hu 等人开发了一个反向传播(BP) 前馈神经网络模型来攻击AES 算法[13], 以超过40% 的概率恢复明文的整个字节, 以超过89% 的概率恢复明文的一半以上的字节, 一定程度上可为暴力攻击降低计算复杂度. 2019 年,Gohr 首次将基于深度学习的差分密码分析与传统差分密码分析进行对比[14], 提出了利用深度学习对减轮的SPECK32/64[15]的差分攻击. 文献[14] 表明, 神经网络可以用来产生与公开的现有技术水平相当的攻击, 对抗现代分组密码的简化版本. 文献[14] 利用神经网络训练了SPECK 的5—8 轮差分区分器, 且区分准确率高于传统差分区分器. 同时, 文献[14] 在此基础上结合贝叶斯优化算法提出一种新的密钥搜索策略, 并结合该策略对11 轮的SPECK 进行密钥恢复攻击, 且计算复杂度低于传统分析手段. 这一成果一经发布就引起了密码学界对深度学习技术的研究热潮. 2020 年, So 等人开发了一个基于深度学习的通用自动密码分析模型[16], 并成功破解了基于纯文本密钥的SIMON32/64 和SPECK32/64[15]. 然而, 文献[16] 中的模型只能破解密钥空间有限的密码, 通用性较差. 在密码分析上, 结合深度学习技术和传统密码分析理念的工作并不多. 2021 年, Benamira 等人在EUROCRYPT 发表了对文献[14] 的工作的深入解释和一些改进, 提出了结合传统机器学习算法和差分分布表的替代策略[17].

对于已经成为研究热点的神经网络差分区分器模型, 我们发现两个未得到充分研究和解决的问题: 一是神经网络差分区分器面对密码算法本身不同的运算部件的表现如何; 二是对于同一种密码, 什么因素会影响神经网络差分区分器的准确率. 对此本文进行了以下三项工作, 并得到相应的结果:

(1) 构造了Speckey[18]和LAX32[19]两类密码的神经网络差分区分器, 并基于密码算法的线性运算部件进行对比分析. 其中Speckey 的有效区分器最高为7 轮, 准确率为0.69; LAX32 的有效区分器最高为4 轮, 准确率为0.55.

(2) 以SIMON32/64 为例, 测试并总结了输入数据所含信息量对神经网络差分区分器准确率的影响.实验结果表明在一定范围内神经网络学习到的信息越多, 其区分准确率也会提高, 差距最高可达0.18. 当提供给神经网络的信息增多到一定程度, 神经网络将不能继续利用更多的信息来提高区分准确率.

(3) 对11 轮的SIMON32/64 进行最后一轮子密钥恢复攻击. 在选择明密文对数为28时, 在1000 次攻击中的成功率为95.6%.

2 神经网络差分区分器模型

传统差分区分器的构造就是找到一条高概率的差分. 在输入差分确定的情况下, 通过观察一对密文的差分是否符合输出差分, 来判断这是真实密文对还是随机数据. 利用神经网络训练差分区分器实际要达到的效果也是类似的, 只是方法有所不同. 神经网络差分区分器的训练是一个挖掘和提取明密文数据特征并进行分类的过程, 所以需要事先生成训练数据. 本文构造区分器所采用的是深度残差神经网络[20], 相比其他网络结构, 残差网络在提高网络深度和特征提取上都具备比较大的优势. 文献[16] 中提出了一种基于残差块的神经网络区分器, 并应用于减轮的SPECK 密码. 同样地, 本文也是基于深度残差网络建立神经网络差分区分器模型, 下面介绍具体结构和数据生成过程.

2.1 神经网络结构

本文的网络包括3 个部分, 共5+2i(1≤i ≤10) 层, 由输入部分、特征提取部分和分类部分组成,网络结构如图1 所示.

(1) 输入部分. 输入部分包括输入层和初始卷积层. 因为训练面向16 比特的字结构, 输入层的输入数据格式为16i×1 (i为正整数, 可根据输入信息的长度来调整). 之后将输入数据整形(Reshape)为i×16 的格式, 并连接到初始卷积层, 即位片层. 该层由一个内核大小(kernel size) 为1 的1D-CNN (一维卷积神经网络), 一个批量归一化(batch normalization) 和一个ReLU (线性整流单元) 激活函数组成. 其中1D-CNN 包括32 个滤波器, 初始卷积层的输出为32×16 的矩阵, 这也是之后残差层所需的输入数据格式. 具体结构如图1(a) 所示.

(2) 特征提取部分. 输入数据已经整理好以后, 神经网络就要从中提取数据特征, 特征提取主要由残差网络来实现. 残差网络(residual network), 简称Resnet, 由一个或多个残差块组成. 此处使用的残差块包括两层卷积网络和一个连接输入输出的旁路(shortcut). 旁路的出现实际上是使用一般意义上的有参层来直接学习残差, 这比直接学习输入、输出间映射要容易得多, 也有效得多. 其中卷积层采用的是内核大小为3 的1D-CNN, 同时后面连接一个批量归一化和一个ReLU 激活函数. 该部分最终将得到一个32×16 的特征张量, 这一部分的残差块个数可取1 到10, 一个残差块的具体结构如图1(b) 所示.

图1 经网络差神分区分器模型Figure 1 Neural network differential partition divider model

(3) 分类部分. 分类部分包括两层全连接网络和一个输出单元, 这三者都属于感知机结构. 感知机是神经网络的基础模型, 用于线性二分类, 其输入是分类对象的特征向量, 输出则是输入的加权和. 对第二部分提取出来的数据特征, 要进行分类. 特征提取得到的数据格式为32×16 的矩阵,Reshape 为512×1 的向量输入到第一层全连接网络(512 to 64), 得到64×1 的向量, 再输入到第二层全连接网络(64 to 64), 得到64×1 的向量. 每层全连接层都要经过批量归一化和ReLU激活函数. 最后得到的64×1 的向量被一个输入为64, 输出为1 的感知器接收并进行评估. 该感知机的输出经过激活函数—Sigmoid 函数, 得到最后的分数, 该分数位于(0,1) 区间, 把分数大于0.5 的对象判为真实密文对, 小于等于0.5 则判为随机数据. 具体结构如图1(c) 所示.

2.2 数据生成

神经网络模型的产生需要训练数据和验证数据, 这两类数据都是由随机数生成器产生的, 其中验证数据是用来防止训练过拟合. 神经网络差分区分器和传统差分区分器一样, 要先确定输入差分, 再得到完整的区分器. 神经网络区分器所需要的数据是给定输入差分的密文对和随机密文对以及对应的标签, 这样做的目的是让神经网络区分器对这两类密文进行区分, 达到差分区分器的效果.

数据生成过程中, 首先, 生成n个随机明文对Pi和初始密钥Ki以及对应的标Yi(Yi= 1 或0); 其次, 对于Yi= 1 的数据, 明文对的差分为固定差分Δ. 对于Yi= 0 的数据, 明文对的差分随机; 然后, 用Ki对所有的明文对进行加密, 得到密文对Ci和对应的标签Yi; 最后, 对Ci进行一些不同的操作并二进制化得到最后的Xi和Yi作为输入数据.

3 基于不同线性部件的两类ARX 密码神经网络差分区分器的构造

2.1 节介绍的神经网络模型最开始应用于SPECK 密码, 而对其他密码的攻击效果目前还有待研究.考虑到Speckey 和LAX 这两类密码的线性运算具有极大相似性, 并且缺乏对其相关的分析结果, 我们选择对Speckey 和LAX 密码进行神经网络差分区分器的训练. 本文所用到的符号解释见表1.

表1 符号说明Table 1 Symbol description

3.1 Speckey 和LAX 简介

Speckey 密码[18]是Alex 等人在2016 年提出的一类ARX 密码, 它相当于SPECK 密码算法的一个变体. 更准确地说, Speckey 是改变了子密钥异或运算过程的SPECK32, 分组大小为32 bit. 其一轮加密包括循环移位、按位异或运算和模加运算等三类运算. 设第i轮的输入为(Li-1,Ri-1), 轮密钥为Ki-1的Speckey 密码的一轮加密过程如图2 所示.

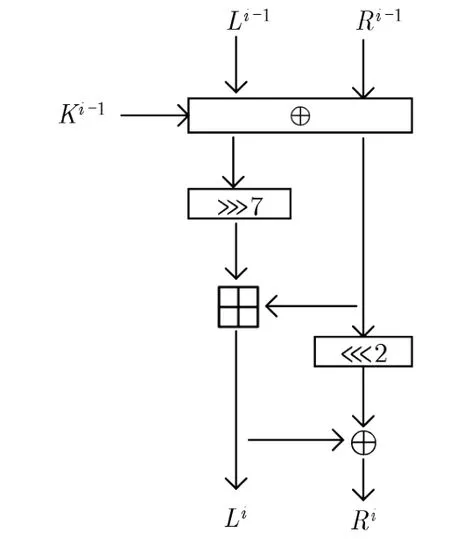
图2 Speckey 轮函数Figure 2 Speckey round function

LAX 密码[19]则是Dinu 等人在研究可证明安全性的ARX 设计策略时提出的, 它是一类只使用模2加法和GF(2) 仿射函数的密码, 是一种具有2n比特分组大小的分组密码结构, 实验采用的是分组大小为32 bit 的密码LAX32. 事实上, LAX 是根据Speckey 的结构来设计的, 它将Speckey 的所有线性运算替换为更一般的线性置换. 因此, 两者唯一的区别在于线性部件不同. LAX 第i轮的轮函数如图3 所示, 其中仿射变换是n比特的向量与n×n的矩阵L相乘, 可表示为:L(x)=L·x.

图3 LAX 轮函数Figure 3 LAX round function

3.2 构造Speckey 和LAX32 神经区分器

尚未有公开文献对Speckey 和LAX32 进行基于神经网络的差分分析, 我们训练了这两种密码的神经网络差分区分器并测试其区分真实密文对和随机数据的准确率. 选择这两种密码的主要原因是这两个密码在运算部件上的区别仅存在于线性运算. 除了线性运算部件, 它们的轮密钥加运算是相同的, 非线性运算也都是发生在轮密钥加之后的模216加运算. 这样, 通过对比两者的训练结果, 可以推出密码的线性运算部件对抵抗神经网络差分分析的影响. 同时, 我们设计了一个简单的实验来对比神经网络差分区分器和传统差分区分器在区分Speckey 和LAX32 时的不同表现.

3.2.1 神经网络差分区分器的构造

选择输入差分为Δ = 0x0040/0000, 加密生成107bit 的训练数据集和106bit 的验证数据集以及106bit 的测试数据集. 此外, 神经网络模型的参数选择如表2 所示.

表2 模型参数Table 2 Model parameter

对于Speckey 密码, 训练了其5—8 轮的神经网络差分区分器. 对于LAX32, 训练了其3—5 轮的神经网络差分区分器. 若输入数据经过神经网络差分区分器的输出大于0.5, 则将输入数据判断为真实密文对,否则判断为随机数据. 用107bit 的训练数据集和106bit 的验证数据集来进行训练, 所有数据遍历一次称为一个epoch, 共进行100 个epoch 的训练, 记录下每一个epoch 的准确率和损失函数值. 其中训练5 轮Speckey 神经网络差分区分器的准确率和损失函数随epoch 变化分别如图4 和图5 所示, 训练3 轮LAX32 神经网络差分区分器的准确率和损失函数随epoch 变化分别如图6 和图7 所示.

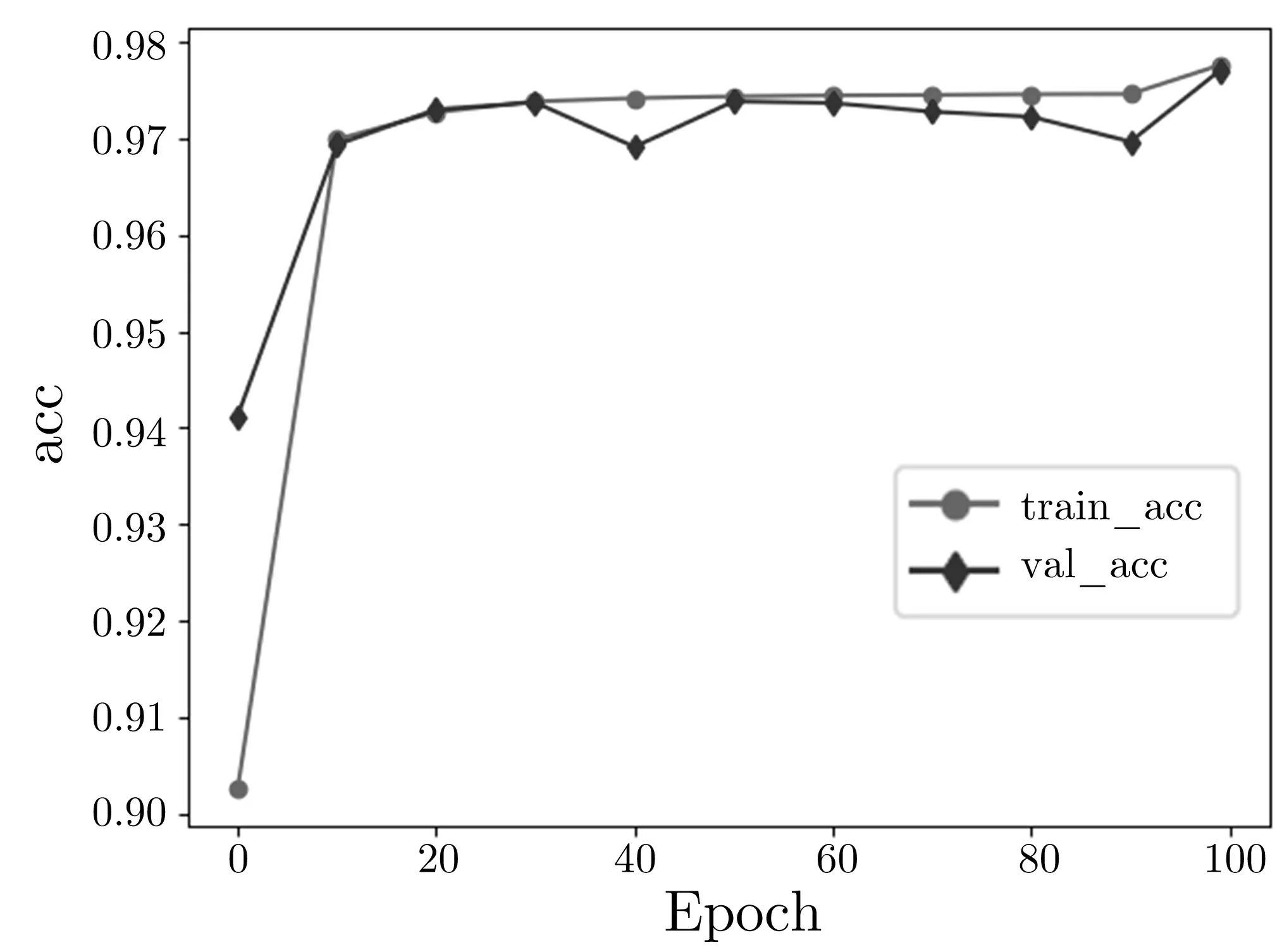
图4 准确率变化(5 轮Speckey)Figure 4 Change of accuracy (5 rounds Speckey)

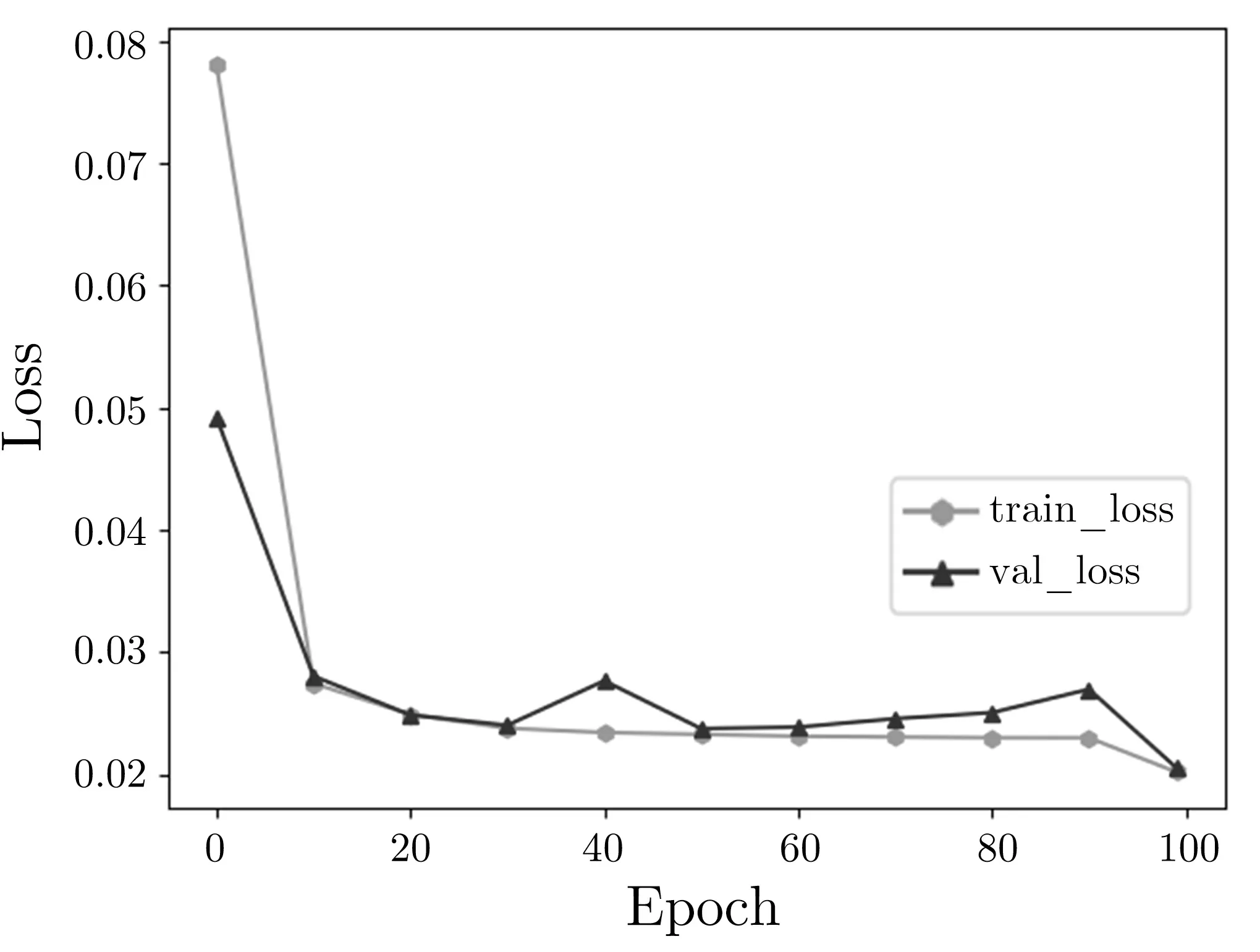
图5 损失函数变化(5 轮Speckey)Figure 5 Change of loss function value(5 rounds Speckey)

图6 准确率变化(3 轮LAX32)Figure 6 Change of accuracy (3 rounds LAX32)

图7 损失函数变化(3 轮LAX32)Figure 7 Change of loss function value (3 rounds LAX32)

以上是对训练过程的一个描述和记录, 对于训练好的神经网络差分区分器, 则用106bit 的测试数据集来测试其准确率. Speckey 和LAX32 的测试结果如表3 所示.

表3 Speckey 和LAX32 的测试准确率Table 3 Test accuracy of Speckey and LAX32

3.2.2 基于实验的传统差分区分器的构造

为了对比神经网络差分区分器和传统差分区分器的区分效果, 我们针对5 轮Speckey 和3 轮LAX32设计了简单的对比实验, 构造了5 轮Speckey 和3 轮LAX32 基于实验的传统差分区分器. 主要分为以下两个步骤:

(1) 搜索高概率差分. 由于传统差分区分器的构造大多是理论上的, 并且其区分效果的评估指标是差分概率, 无法与神经网络区分器的测试准确率进行横向对比. 因此, 我们通过实际实验来选取高概率的差分. 选择输入差分为Δ = 0x0040/0000 的n个明文对P1,P2,··· ,Pn, 加密r轮(对Speckey 加密5 轮, 对LAX32 加密3 轮) 得到密文对C1,C2,··· ,Cn, 再获得密文对的截断差分值(分别获取左半部分密文分组和右半部分密文分组的差分)ΔC1,ΔC2,··· ,ΔCn, 分别保存其中出现次数最多的100 个输出差分. 最后将上述过程迭代t次, 再从所有保存的差分中选择频率最高的100 个差分作为该传统区分器的输出差分, 这是借鉴了多重差分分析[21]和截断差分[22]的思想.

(2) 测试传统差分区分器的区分准确率. 以输入差分Δ = 0x0040/0000 生成带标签的测试数据, 将传统差分区分器的判定结果与标签进行对比得到测试准确率. 其中5 轮Speckey 和3 轮LAX32测试的都是由左半部分密文差分作为输出的截断差分区分器, 因为搜索得出左半部分密文差分出现的最高频次大于右半部分密文差分出现的最高频次.

当选择n= 107,t= 5 以及测试数据量为106bit 时, 基于实验的传统差分区分器测试结果和相应的神经网络差分区分器的对比结果如表4 所示. 值得一提的是, 每一次迭代得到的100 个差分重复率极高,频次最高的差分一直不变, 并且出现次数明显高于频次第二高的差分. 也就是说, 最后保存的100 个差分至少包含一个最高概率差分和其他多个较高概率差分.

表4 Speckey 和LAX32 的传统区分器和神经网络区分器对比Table 4 Comparison of conventional and neural network discriminators with Speckey and LAX32

3.3 实验结果分析

首先, 从神经网络差分区分器的准确率可以看到, 对于5—7 轮Speckey 和3—4 轮LAX32, 其区分器的准确率都明显高于0.5. 也就是说, 相应区分器都是有区分效果的, 并且区分效果是非常显著的, 5 轮Speckey 密码的神经网络差分区分器准确率甚至达到了0.95. 因而, 神经网络模型在训练过程中可以成功提取这两种密码的密文数据特征并实现正确分类. 而对于8 轮Speckey 和5 轮LAX32, 其神经网络差分区分器的准确率都低于0.5, 按照本文的定义是不具备区分效果的.

其次, 从表3 的结果可以看到, Speckey 的有效的神经网络差分区分器最多可达8 轮, 而且LAX32 最多可达5 轮. 当两类密码的轮数相同时, 即对于5 轮神经网络区分器, Speckey 的区分准确率明显高于LAX32. 可见, 神经网络差分区分器对Speckey 的区分效果明显高于LAX32. 这两类密码的分组大小都是32 bit, 加密中的唯一非线性运算都是模216加运算, 轮密钥加的位置也相同, 最大的不同就是线性运算部件. 结合实验结果, 可以看出轮数较低时, 在抵抗基于神经网络的差分攻击方面, 一般的线性仿射要比循环移位效果更好. 这是因为在加密过程中线性仿射的扩散效果要更好一些, 而这一点在传统差分分析中也有相同的表现[18,19].

文献[18]和文献[19]给出了Speckey 和LAX32 的最佳减轮差分搜索结果,此处列举3—5 轮Speckey和LAX32 的自动搜索结果并与3.2 节测试结果进行对比分析, 具体数据如表5 所示.

表5 3—5 轮Speckey 和LAX32 的自动搜索结果和测试准确率对比Table 5 Comparison between 3–5 round Speckey and LAX32 automatic search results and test accuracy

在轮数为5 时, Speckey 的最佳差分概率为2-9, 而LAX32 的最佳差分概率为2-11. 此外, 我们发现4 轮LAX32 的最佳差分概率和5 轮Speckey 的最佳差分概率是相同的, 都是2-9. 但5 轮Speckey的神经网络差分区分器准确率大约为4 轮LAX32 的准确率的2 倍. 由此说明, 扩散效果对神经网络差分区分器准确率的影响比传统差分概率要更明显, 但扩散效果越好, 安全性越高这一整体趋势是相同的. 设计者在设计密码时, 需要针对现有的各种攻击进行安全性分析. 当进行对基于深度学习的差分攻击的安全性分析时, 本文的实验结果对线性部件的设计可提供参考价值.

另外, 表4 的结果展示的是在利用相同的数据量时传统区分器和神经网络区分器的简单对比. 由于神经网络区分器所能利用的信息更多, 而我们构造的基于实验的传统差分区分器只能利用差分信息, 所以神经网络差分区分器的准确率更高. 这一结果是不难理解的, 而这也正是神经网络区分器的优势所在, 可以从密文数据中学习到除差分以外的其他信息来提升区分效果. 传统差分区分器想要达到类似的区分准确率则要收集大量的差分信息并存储为一个差分分布表, 比如文献[14] 给出的Speck32/64 的最佳差分分布表的存储需要35 GB 的读写空间, 而一个神经网络的权重文件大约为600 KB.

4 基于不同输入信息的神经区分器对SIMON32/64 的分析

经过对Speckey 密码和LAX 密码的神经网络差分区分器的构造, 我们继续利用神经网络模型对SIMON 密码进行分析. 在分析过程中, 我们结合文献[17] 的工作和SIMON 密码算法的轮函数发现: 可以通过改变输入数据的格式来改变传递给神经网络的有关密文数据的信息量, 以此探究输入数据包含的信息量对神经网络区分器准确率的影响. 此外, 我们在此基础上对11 轮SIMON 密码进行最后一轮子密钥恢复攻击, 得到1000 次攻击的成功率.

4.1 SIMON 密码算法简介

SIMON 密码[15]是一类轻量级分组密码, 在2013 年由美国国家安全局提出, 在发布之后受到广泛关注和分析. SIMON 密码是典型的Feistel 结构, 一轮加密包括循环移位、按位异或运算和按位与运算等三类运算. 因此, 它也属于广义的ARX 结构. SIMON 密码族作为一类分组密码, 其分组大小可表示为2n,单位是比特,n的值可以为16、24、32、48 和64, 对应的密钥长度为mn比特. 因此, 一个分组大小为2n, 密钥长度为mn的SIMON 密码可用SIMON2n/mn来表示. 设第i轮的输入为(Li-1,Ri-1), 轮密钥为Ki-1的SIMON 密码的一轮加密过程如图8 所示.

图8 SIMON 密码轮函数Figure 8 Round function of SIMON

4.2 输入信息量对神经区分器准确率的影响

在密码分析中, 差分攻击是分析分组密码最有效的方法之一. 本实验基于传统差分分析方法, 分别构造了SIMON32/64 的7—10 轮的神经网络差分区分器并测试其准确率. 训练该区分器采用的输入差分为Δ= (0x0000/0040), 该差分可以确定性地传递到第二轮输入差分0x0040/0000[23]. 由此生成的训练数据量为107bit, 验证和测试数据量为106bit. 此外, 模型的参数选择为: 训练期数(Epochs) 为100, 批次(Batch Size) 为5000, 优化算法(Optimizer) 选择了Adam 算法, 损失函数(Loss Function) 为MSE. 训练过程与3.2 节类似, 测试结果如表6 所示.

表6 SIMON32/64 的测试结果Table 6 Test result of SIMON32/64

上述实验中的输入数据为密文对的实际值, 若用C0,C1表示密文对, 用C0l,C0r,C1l,C1r分别表示C0,C1的左半部分和右半部分. 输入数据可表示为(C0l,C0r,C1l,C1r), 长度为16× 4. 这一输入是文献[14] 采用的, 而文献[17] 中采用了另一种输入, 并在SIMON32/64 的区分器上达到了更好的效果. 因此, 我们想进一步研究并系统分析输入信息量对神经网络区分器的影响, 于是采用四种信息量不同的输入数据对SIMON32/64 的7 到10 轮差分区分器进行训练. 四类数据分别为(C0l ⊕C1l,C0r ⊕C1r),(C0l,C0r,C1l,C1r),(C0l ⊕C1l,C0r ⊕C1r,t0⊕t1) 和(C0l,C0r,C1l,C1r,t0⊕t1), 其中t0和t1可由式(1)和(2)表示.

根据SIMON 的轮函数, 可以看到t0和t1包含了倒数第二轮的除密钥以外的信息.

4.3 部分密钥恢复攻击

在4.2 节的实验基础上, 进一步对11 轮SIMON32/64 进行部分密钥恢复攻击. 由于第一个子密钥异或发生在SIMON 首次进行非线性运算之后, 进行选择明文攻击的攻击者可以很容易地使他们选择的明文差分出现在第一轮SIMON 的输出中. 因此, 在进行密钥恢复攻击的时候, 可以很容易地把所有区分器再扩展一轮. 本文对11 轮SIMON 的最后一轮子密钥攻击过程如下:

(4) 保存高分密钥. 将所有的密钥值k按照其分数Vk进行降序排列, 留下分数最高的密钥值kmax作为候选正确密钥.

(5) 测试成功率. 将以上攻击过程实施1000 次, 若保存的候选密钥等于正确密钥则判为一次成功的攻击. 对于不同的神经网络差分区分器, 测试其成功率.

4.4 实验结果及分析

4.4.1 输入信息量不同的神经网络区分器测试结果及分析

4.2 节采用的分析方法属于选择明文攻击, 而这四种数据包括了该类攻击中神经网络能利用信息的所有具备代表性的组合. 将输入数据类型不同的神经网络区分器依次表示为Na, Nb, Nc, Nd. 4.2 节的测试结果如图9 所示.

图9 不同输入数据格式下SIMON32/64 的准确率测试结果Figure 9 Test results of accuracy for SIMON32/64 under different input data format

从图9 可以看到, 四种神经网络差分区分器的准确率随着输入数据的改变而发生变化. 这四种输入数据包含的神经网络所能利用的密码先验知识是不同的. (C0l ⊕C1l,C0r ⊕C1r) 只包含选择密文对的差分值信息, (C0l,C0r,C1l,C1r) 包含密文对的差分值和实际值, (C0l ⊕C1l,C0r ⊕C1r,t0⊕t1) 包含密文对的差分值和倒数第二轮的部分差分信息, (C0l,C0r,C1l,C1r,t0⊕t1) 则包含密文对的差分值和实际值以及倒数第二轮的部分差分信息. 可见, 输入数据的信息量是递增的. 根据实验结果, 当可利用的信息量越多, 神经网络差分区分器Na, Nb, Nc 的准确率是递增的, 但Nd 的准确率却没有比Nc 的准确率更高. 前三个区分器的准确率的递增很好理解, 输入数据的信息含量越多, 神经网络能学习到关于密码的知识更多, 对真实密文对和随机数据的区分能力就更强. 这也再一次印证了Ghor 在文献[14] 中对神经网络差分区分器的准确率比传统差分区分器高的原因解释, 神经网络能从密文对中学到除了差分信息以外的密码知识.但对于最后一类输入数据格式, 神经网络差分区分器准确率并没有继续升高, 我们推测原因是最后一类输入数据提供的数据特征太多, 该神经网络在这样一个结构下无法很好地整合这些特征. 这一点可以理解为:该神经网络结构在接受过多的数据信息后, 判断密文对是真实或随机的限制条件过多, 导致神经网络对所有输入数据的评分偏低, 出现一定的分类误差. 因此, 在神经网络模型的超参数确定的情况下, 研究合适的输入数据格式对于得到区分效果较好的神经网络差分区分器是十分有必要的.

在利用本文最好的输入数据格式, 即(C0l,C0r,C1l,C1r,t0⊕t1) 时, 本文和文献[14]、文献[17] 的对比结果如表7 所示.

表7 SIMON32/64 最佳分析结果对比Table 7 Comparison of best analysis results for SIMON32/64

从表7 可以看到: 对于SIMON32/64, 应用文献[14] 的方法训练的7—10 轮差分区分器的测试准确率均比本文的最佳测试结果低, 其中8 轮区分器的准确率相差5%. 同时, 应用文献[14] 训练的10轮SIMON32/64 的测试准确率是0.5, 该准确率对于二分类问题是无效的, 所以应用文献[14] 训练的SIMON32/64 有效区分器最高可达9 轮, 而本文训练的有效区分器可达10 轮. 文献[17] 应用Ghor 的模型[14]训练了SIMON32/64 的8 轮差分区分器并得到了0.834 的准确率, 但只给出了一个测试结果, 没有进行深入的研究, 缺少对比文献[14] 准确率高的原因分析, 也没有给出SIMON32/64 有效区分器的轮数上限. 而我们训练了7—10 轮的SIMON32/64 神经网络差分区分器, 其中8 轮的结果与文献[17] 的结果相当, 准确率为0.837. 同时, 分析了相对文献[14] 准确率提高的原因, 还给出了通过本文方法所训练的有效的SIMON32/64 神经网络差分区分器的最高轮数, 即10 轮.

4.4.2 部分密钥恢复的结果展示及分析

4.3 节的攻击采用的神经网络区分器包括Na, Nb, Nc, Nd, 也就是对于不同的输入数据格式都进行了部分密钥恢复实验. 在此设置下, 选取不同的明文对数所得到的攻击成功率如表8 所示. 当明文对数为n,数据量为2n. 由于9 轮Na 的准确率接近0.5, 不适合用来进行11 轮的密钥恢复攻击(实际攻击结果显示其对所有猜测密钥的评分都相同, 不具备区分能力), 其攻击成功率在数据量为29bit 时等于0, 所以其攻击结果不予展示. 而Nb 在数据量为29bit 时的攻击成功率接近0.1, 为了更好地比较Nb 和其他两类区分器在相同数据量下的攻击效果, 此处只展示利用Nb 的攻击中正确子密钥的分数在所有猜测子密钥分数中的平均排序, 我们把这个值称为krank. 在一次攻击中, 若krank为0, 则该次攻击是成功的,krank越大, 表示误判的子密钥数越多.

表8 不同区分器下的对SIMON32/64 攻击结果Table 8 Attack results of SIMON32/64 under different discriminators

在每一种输入格式下, 我们尝试了不同数据复杂度下的攻击. 从表8 可以看到: 最好的结果是在选择明密文对数为28, 即数据量为29时, 使用Nd 对11 轮SIMON32/64 的最后一轮子密钥进行1000 次攻击, 成功率可达95.6%. 可见, 神经网络差分区分器在差分分析中表现不错, 有较好的区分能力, 并且不需要存储差分分布表, 空间复杂度降低.

5 结束语

我们基于深度学习在分组密码差分分析方面进行研究. 首先, 构造了Speckey 和LAX32 两类密码的神经网络差分区分器, 并取得有效的结果. 我们训练了5—7 轮Speckey 和3—5 轮LAX32 的有效的神经网络差分区分器. 如果把测试准确率在0.5 以上的区分器视为有效的区分器, Speckey 的有效区分器可达到7 轮, 且准确率为0.69. LAX32 的有效区分器可达到4 轮, 且准确率为0.55. 在经过以上研究之后, 继续对SIMON 密码进行分析, 在分析过程中发现改变神经网络的输入数据形式会影响其差分区分器的准确率. 当输入数据所含信息量不同时, 区分器的最高准确率和最低准确率相差18%. 在构造完神经网络差分区分器后, 我们进一步对11 轮SIMON32/64 密码进行最后一轮子密钥恢复攻击, 在选择明密文对数为n=28时, 1000 次攻击中捕捉到正确密钥的成功率为95.6%.