无假阳性的可验证通配符可搜索加密

赵 博, 刘晋璐, 秦 静,2

1. 山东大学 数学学院, 济南 250100

2. 中国科学院信息工程研究所信息安全国家重点实验室, 北京 100093

1 引言

计算机网络的迅速发展和信息化进程的加速, 使得各领域中的数据飞速增长, 用户本地的存储空间已经无法满足这种需求. 此时, 云计算[1–4]服务为解决数据存储问题提供了重要的技术支撑. 借助互联网技术尤其是5G 通讯技术可以快速地将这些数据存储到具有强大数据存储和处理能力的云服务器上. 然而用户将数据外包给云服务器使数据脱离了物理控制, 存储在云服务器上的数据可能会遭受来自云存储服务器供应商的内部攻击或来自黑客的外部攻击, 导致用户隐私数据泄露. 为了保护云数据安全, 通常在数据外包之前对数据进行加密, 然后再上传到云服务器. 但是传统的加密算法使得密文不可区分, 因此搜索和定位密文数据变得困难.

为了解决上述问题, Song 等人[5]首次提出基于密文线性扫描的对称可搜索加密方案. 对称可搜索加密[6–8]是一种支持用户在密文上进行关键词检索的密码学原语, 用户使用可搜索加密技术加密明文数据,其他用户(包括加密者) 通过该协议可以实现对密文的关键词检索. 2004 年Goh[9]提出安全索引概念,并利用伪随机函数和布隆过滤器构建了索引形式为文件-关键词(称为正向索引) 的对称可搜索加密协议,在搜索某个关键字时利用BF 可以快速判断某元素是否在某个集合中的性质判定密文文件是否包含某个关键词, 搜索复杂度与文件总数相关. 与Goh 方案类似, Chang 等[10]在2005 年通过预先建立字典生成加密索引构建了可搜索加密方案.

上述方案只支持完整关键词的搜索. 然而, 在实际应用中, 用户可能不能或不需要输入完整的关键词,通配符可搜索加密[11–13]技术的提出解决了该问题. 在通配符可搜索加密中, 用户可以使用通配符表示询问关键词中不能具体表达的字符, 从而实现关键词的部分匹配而不局限于完整匹配. 通配符主要有“?” 和“*” 两种, “?” 代表一个字符, 称其为单字符通配符, “*” 可以代表任意多个字符, 称其为多字符通配符. 例如, Alice 想要搜索存储在云端的所有pdf 文件, 则可以使用“*” 表示文件名称, 从而利用“*.pdf” 搜索到所有的pdf 类型文件. 又如, Alice 想要搜索在2021 年10 月的某一天存储的一份文件, 但忘记了具体的存储日期, 这时Alice 不需要分别搜索10 月份每一天存储的文件, 而可以使用“*102021” 搜索到10 月份所有的文件, 从而筛选得到目标文件. 2011 年, Bösch 等人[14]利用布隆过滤器(bloom filter, BF) 与伪随机函数构造联合通配符对称可搜索加密方案, 该方案的索引为正向索引, 为了实现通配符搜索, 在索引生成阶段, 需将每个文件包含的所有关键词及每个关键词通配符形式的所有变体插入到文件对应的BF中. 2016 年, Hu 等人[15]提出一种多功能可搜索加密方案, 同时支持通配符搜索、近似搜索、模糊搜索、分离关键词搜索和对文件的更新. 该方案的索引为关键词-文件形式(称为倒排索引), 为了实现通配符搜索, 在陷门生成时, 需要对关键词通配符所有可能形式进行枚举. 上述两个方案通过在索引或陷门生成时枚举关键词通配符形式的所有变体实现通配符搜索, 效率低且存储或通讯负担大. 2012 年, Suga 等人[16]对关键词中每个字符提取位置特征构造了一个支持多种类型搜索的可搜索加密方案. 该方案的索引为倒排索引, 在索引生成阶段, 按照字符位置级联字符的方式提取特征集合, 然后将特征集合中每一个元素映射到BF 中. 由于提取特征方式的局限性, 该方案只能支持单字符通配符搜索. 2016 年, Hu 等人[17]改进文献[16] 中的特征提取方式, 利用关键词每个字符的正序、倒序以及存在性, 提出了一个多字符通配符搜索方案. 同年, Zhao 等人[18]提取单字符绝对位置, 两字符相对位置特征也解决了多字符通配符搜索问题. 2019 年, 于文等人[19]基于Hu 的方案利用隐藏向量加密技术, 将索引过滤器和陷门过滤器分别看作索引向量和查询向量, 然后对BF 加密提出了一个更加安全的通配符搜索方案. 该方案的数据保密性更强,而且在搜索时避免了陷门和索引的两个BF 之间比特值的一一匹配, 提高了搜索效率. 但在该方案中, 过滤器的每一比特都要通过一个伪随机函数进行加密, 增大了索引存储.

可以看出, 现有的通配符可搜索加密方案基本都基于布隆过滤器构造索引, 但是布隆过滤器一个显著的弊端就是存在假阳性, 即搜索时会返回多余的文件给用户, 这不仅带来不必要的网络通讯量, 而且增加了用户对密文文件处理的负担. 另外, 现有的通配符可搜索加密方案只考虑了半诚实的服务器[20], 但是在商业云计算服务中, 云服务器可能是自私的, 为了节省计算量或者下载带宽, 服务器可能会返回错误的搜索结果或者部分搜索结果. 针对上述问题, 本文设计了一个无假阳性的可验证通配符可搜索加密方案. 主要工作如下:

(1) 无假阳性. 本文将一种特殊的通配符搜索类型—前缀类型, 转化为范围搜索. 具体地, 对关键词字典进行编码, 使得每一个关键词对应一个二十六进制数字. 这种编码方式保证了编码数值大小顺序等价于原始关键词的字典顺序. 然后将所有的关键词编码存储在一个数组中, 搜索时将询问的单字符通配符分别替换为a 与z, 并对替换后的两个关键词进行编码, 索引数组中的编码值介于这两者数值之间的关键词即为搜索结果.

(2) 有序二叉位图树(ordered binary bitmap tree, OBBT) 索引结构. 当关键词字典包含的关键词较多, 使用数组索引进行线性查找的搜索效率较低, 为此我们提出有序二叉位图树索引. OBBT 通过提取关键词字符每一位特征, 将其存储在树的各层结构中, 树的第i层表示关键词第i个字符的存在性, 每个节点用位图表示该层包含的所有字符, 叶子节点存储该路径包含的所有可能关键词编码值, 使得数组的大范围搜索转化为其子范围搜索. 进一步地, 为了提高在每个叶子节点内的搜索效率及保证索引关键词的隐私性, 令每个叶子节点数组的元素按照数值大小进行排序并利用保序加密对编码值进行加密, 匹配出介于两个编码密文值区间的所有关键词即为搜索结果.

(3) 搜索结果可验证. 为了验证搜索结果的正确性, 在每个编码值的后面级联一个验证标签(验证标签是对关键词信息、密文hash 校验值、密文标志符进行加密). 用户与服务器第一轮交互之后,云服务器返回一个验证标签集. 用户解密验证标签集中的每一个标签, 得到关键词及包含每个关键词的文件标识符与密文hash 校验值. 然后用户对比询问关键词和解密得到的关键词判定返回密文标识符的正确性. 第二轮交互云服务器返回密文, 用户利用hash 值校验返回密文的正确性和完整性.

2 预备知识

2.1 符号说明

首先给出本文中用到的符号说明.

2.2 伪随机置换

定义1 (伪随机置换[21])F:{0,1}k×{0,1}l →{0,1}l是一个函数族, 若F满足以下两个条件则称F是(t,ε,q) 伪随机置换.

(1) 任意给定x ∈{0,1}1和密钥k ∈{0,1}k都能有效的计算F(k,x).

(2) 对于任意t时间多项式时间算法A做至多q次自适应询问都有

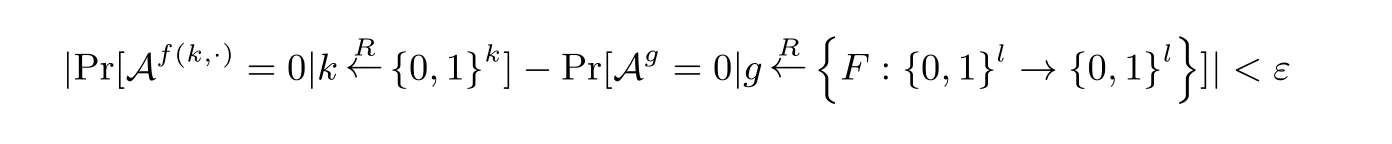
2.3 保序加密

定义2 (保序加密) 对于群R中的子集A,B, 满足关系|A|≤|B|. 函数f:A →B为一个保序函数,即对于∀i,j ∈A有f(i)＜f(j) 当且仅当i ＜j. 对于一个加密算法Π=(Gen,Enc,Dec), 明文空间和密文空间分别为M,C. 如果Enc(k,·) 是一个满足上述条件的保序映射函数, 那么Π = (Gen,Enc,Dec) 就是一个保序加密算法.

定义3 (random order preserving function, ROPF[22]) 保序加密方案Π = (Gen,Enc,Dec), 明文空间M, 密文空间C, 满足|D|≤|R|. 方案Π 被认为是ROPF 安全的, 如果对于任意概率多项式敌手A, 存在一个可忽略函数negl 使得,

2.4 PCPA 安全

定义4(pseudo-randomness against chosen plaintext attacks,PCPA[6]) 令SKE=(Gen,Enc,Dec)表示为一个对称加密方案,A表示一个敌手, 考虑如下概率实验PCPASKE,A(λ):

(1) Gen(λ) 产生一个密钥K.

(2) 敌手A允许访问随机预言机EncK(·).

(3)A输出一个信息m.

(4) 两个密文文本c0,c1按照如下方式产生,c0←EncK(m),c1从SKE 的密文空间中随机选取. 随机选择一个比特b, 将cb发送给敌手A.

(5)A允许访问加密随机预言机, 经过多项式次询问之后输出一个比特b′.

(6) 如果b′=b, 实验输出1, 否则输出0.

我们说SKE 是PCPA 安全的, 如果对于任意概率多项式(probabilistic polynomial-time, PPT) 敌手A, 存在一个可忽略函数negl 使得,

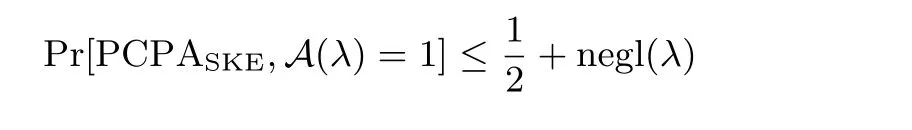
2.5 系统模型

如图1 所示, 系统模型包括三个实体, 数据拥有者、云服务器和数据使用者. 假定数据拥有者和数据使用者是诚实可信的, 会忠实执行协议. 云服务器是半可信且好奇的[23], 即其可能为了节省其计算量或者下载带宽而返回错误的搜索结果或者部分搜索结果.

图1 系统模型Figure 1 System model

数据拥有者拥有一个文档集D, 想要外包给云服务器. 首先, 为了确保数据的安全性, 将文档集加密得到密文文档C. 其次, 为了对密文文档进行高效的检索及验证搜索结果, 从文档集中提取关键词字典, 并利用关键词字典构建一个可验证的安全索引I, 最后将索引I和密文C上传到云服务器. 数据使用者经过数据拥有者授权, 利用数据拥有者提供的密钥生成搜索陷门TQ并发送给云服务器. 云服务器利用陷门在索引上搜索并返回搜索结果Tagsecond, 数据使用者利用Tagsecond与服务器交互验证搜索结果的正确性和完整性.

定义5 (无假阳性的可验证通配符可搜索加密系统) 无假阳性的可验证通配符可搜索加密系统Π 由以下算法组成:

(1) KeyGen(λ)→(sk,k): 输入安全参数λ, 数据拥有者调用密钥生成算法, 输出密钥k和密钥集sk.

(2) Enc(k,D)→C: 输入密钥k和文档集D, 数据拥有者调用加密算法, 输出密文文档C.

(3) BuildIndex(sk,D)→I: 输入密钥集sk 和文档集D, 数据拥有者调用索引建立算法, 输出索引I.

(4) Trapdoor(sk,Q)→TQ: 输入密钥集sk 和询问关键词Q, 数据使用者调用陷门生成算法, 输出陷门TQ.

(5) Search(TQ,I)→Tag: 输入陷门TQ和索引I, 云服务器调用搜索算法, 输出验证标签集Tagsecond.

(6) Verify(sk,Tag)→0/1: 输入验证标签集Tagsecond和密钥集sk 数据使用者调用验证算法与服务器进行交互验证, 验证搜索结果.

2.6 安全模型

首先介绍一些辅助性概念.

定义6 (查询历史) 一个方案的查询历史包括: 文档集合D= (D1,D2,··· ,Dm) 以及询问列表Qk=(q1,q2,··· ,qk), 将查询历史表示为H=(D,Qk).

定义7 (视图) 查询历史的视图包括: 加密文件Encsk(D), 安全索引Encsk(Ikw) 和陷门Tr(Qk), 将视图表示为V(H)={Encsk(D),Encsk(Ikw),Tr(Qk)}.

定义8 (访问模式) 一个查询历史的访问模式指的是询问Qk的搜索结果AP ={D(q1),D(q2),···,D(qk)}.

定义9 (轨迹) 一个查询历史的轨迹指的是云服务器能捕捉到的信息, 将查询的轨迹表示为T(H) ={AP,|·|},|·| 表示索引结构本身的特性.

定义10 (非适应性语义安全) 令Π = (KeyGen,Enc,BuildIndex,Trapdoor,Search,Verify) 表示一个无假阳性的可验证通配符可搜索加密方案,S表示一个模拟器, 非适应性语义安全描述如下:

·RealΠ,A(λ) 的具体过程如下:

(1) 挑战者运行KeyGen(λ)→K.

(2) 敌手选择文档集合D.

(3) 挑战者运行Enc(k,D) 和BuildIndex(sk,D) 算法得到Encsk(D) 和索引Encsk(Ikw). 同时运行Trapdoor(sk,Q) 算法为敌手的询问列表Qk生成陷门Tr=(Tr1,Tr2,··· ,Trk).

(4) 输出视图V=(Encsk(D),Encsk(Ikw),Tr(Qk)).

·SimΠ,A,S(λ) 是如下一个模拟过程:

(1) 敌手输入查询历史H.

(2) 模拟器S根据T(H) 模拟Encsk(D),Encsk(Ikw),Tr(Qk).

(3) 输出视图V′= (Encsk(D),Encsk(Ikw),Tr(Qk)),. 我们称方案是Π 是非适应性语义安全的, 如果对于任意多项式时间的敌手A, 均存在一个多项式时间模拟器S, 使得Real 与Sim 的视图V和V′是计算不可区分的.

3 无假阳性的可验证通配符可搜索加密方案

为了设计一个在加密数据上安全有效的搜索方案, 需要做三个重要的设计:

(1) 建立安全的索引和陷门数据结构.

(2) 一个高效的匹配询问和索引中关键词的搜索算法.

(3) 可以将安全索引和搜索算法整合的在一起的隐私保护机制.

3.1 节阐述设计(1)(2) 的主要步骤, 为了便于理解先介绍在明文数据下的索引结构和搜索算法. 3.2 节展示带有安全机制和隐私保护的通配符搜索方案.

3.1 明文OBBT 索引

我们将一种特殊的通配搜索类型—前缀搜索, 转化为范围搜索. 具体来讲, 对于给定的关键词字典WD={kw1,kw2,··· ,kwn}, 首先使用二十六进制对每个关键词kw 进行编码, 即将英文字符a—z 与0—25 分别一一对应, 并将所有的数字级联为一个整数codekw. 例如, searchable 对应的二十六进制编码为codesearch= 18×269+4×268+···+4×260. 关键词按照该规则得到的编码值顺序与关键词按照字典排序结果是一致的. 将所有的关键词编码值存储在一个数组中, 对于任意的带“?” 通配符的搜索关键词Q, 将关键词中的“?” 替换为a, 对应的关键词编码记为codemin; 将关键词中“?” 替换为z, 对应的关键词编码记为codemax. 依据编码规则, 与Q匹配的关键词编码数值一定介于codemin与codemax之间.

当关键词字典的空间较大时, 使用数组存储所有的关键词编码进行线性查找, 搜索效率较低, 为此我们设计了一个OBBT 索引将数组分隔并划分到不同的叶子节点中, 使得大范围的数组搜索转化为其子范围搜索. OBBT 是利用逐字符对比判断每个字符是否相同, 进而判定关键词是否存在. 也就是说, OBBT提取出关键词的每一字符特征, 将其存储在二叉树的各层中. 二叉树的第i层表示关键词第i个字符的存在性, 每个节点用位图表示该层包含的所有字符. 其中根节点为26 位的位图表示首字符的存在性, 第二层开始每个节点为13 位的位图(左节点代表a—m, 右节点代表n—z). 叶子节点存储该路径包含的所有可能关键词编码值-关键词对. 搜索时, 对比每一层的位图是否包含询问关键词的特征, 定位到与询问关键词匹配的叶子结点, 从而进入叶子节点的子范围搜索. 进一步, 为了提高每个叶子节点内部搜索效率, 令每个叶子节点数组的元素按照编码值数值大小进行排序, 匹配出介于codemin, codemax区间的关键词即为搜索关键词. 下面具体介绍OBBT 的构建.

(a) OBBT 预置

给定关键词字典WD={kw1,kw2,··· ,kwn}, 假设关键词长度都为l, 则二叉树的高度为l. 二叉树根节点为26 位的位图(bit map, bm), 其余节点结构为13 位的位图, 叶子结点级联一个数组. 初始化阶段将所有bm 全置为0, 得到二叉位图树.

(b) 字符映射

建立字符与数字之间一个1-1 映射关系, 将英文字母a—z 分别映射到1—26, 通配符“?” 映射到“?”.利用1-1 映射规则将关键词kwi转化对应的特征数组Tkwi.

(c) 特征填充

通过步骤(b) 将关键词字典转化为对应的特征数组集T={Tkw1,Tkw2,··· ,Tkwn}, 并按照如下规则将T中元素逐个填充到OBBT 中. 对于T中任意的数组Tkwi= [θ1,θ2,··· ,θl], 首先填充根节点, 将根节点位图的θ1位置置为1. 接下来填充其他层的节点, 判断数组Tkwi的第j位值θj, 若θj ≤13, 则将第j层的左节点θj位置置为1; 若θj ＞13, 则将第j层的右节点θj-13 位置置为1. 逐层填充直到完成最后一层, 将关键词kwi填充到叶子节点的数组中. 按照上述流程将特征数组集T全部填充到OBBT 中,如图2 所示. 下面以searchable 为例, 描述如何构建OBBT 以及填充关键词.

图2 OBBT 索引Figure 2 OBBT index

首先, 根据关键词长度确定 OBBT 的高度为 10, 按照 (a) 所述构建一个 10 层的全 0 二叉位图树. 其次, 根据 (b) 所述的 1-1 对应规则将字符转化为对应的特征数组: searchable→[19,5,1,18,3,8,1,2,12,5]. 接下来, 将数组填充至OBBT 中, 数组的第一位为19, 将根节点的第19位置为1; 数组的第二位是5, 将第二层的左节点第5 个位置置为1. 依次类推直至填充到最后一层. 最后将关键词searchable 级联在叶子节点.

(d) 编码与排序

按照上述规则将所有的关键词填充到OBBT 中, 每个叶子节点级联该分支所有可能的关键词. 接下来, 将叶子节点所有关键词进行编码和排序. 我们利用二十六进制规则对关键词的每一个字符进行编码,也就是将英文字符a—z 与0—25 分别一一对应, 并将编码后的数字级联得到一个对应的整数. 将每个叶子节点的级联的所有关键词按照如上规则得到编码值-关键词对组, 将其级联在OBBT 叶子节点. 最后, 将每个组的元素按照编码值大小进行排序, 得到有序二叉排序树.

(e) 逐层匹配算法

给一个询问关键词Q, 我们利用逐层匹配算法进行查询. 不妨设Q的第i位为“?”, 将关键词Q按照步骤(b) 通过1-1 对应关系转化为特征数组TQ={θ1,θ2,··· ,?,··· ,θl}; 将Q的第i位替换为a 和z,并利用算法(d) 计算出其对应的编码值, 记为codemin,codemax. 首先将特征数组与根节点进行匹配, 判断位图θ1位的值, 如果该位置为1, 继续搜索; 否则停止搜索, 表示关键词不存在. 接下来判断θ2的值, 如果θ2≤13, 那么搜索第二层的左节点, 并判断θ2位置是否为1, 如果为1 继续搜索, 否则停止搜索; 如果θ2＞13, 则搜索右节点, 判断θ2-13 位置是否为1, 如果为1 继续搜索, 否则停止搜索. 依据上述规则,直到遇见通配符, 跳过第i层, 直接进入第i+1 层, 如果θi+1≤13, 则同时搜索i+1 层的两个左节点;如果θi+1＞13, 同时搜索两个右节点; 直到最后一层匹配结束, 返回叶子节点数组中codemin,codemax区间的所有关键词.

3.2 通配符搜索加密方案

本节展示带有安全机制和隐私保护的通配符方案. 本文方案包括六个多项式时间算法:

- KeyGen(λ): 输入一个安全参数λ, 输出密钥k, 密钥集sk ={skop,skver,skf}, 其中skop是保序加密密钥, sktag是加密标签密钥, skf是伪随机置换密钥.

- Index_Enc(sk,OBBT): 输入OBBT 和密钥sk. 对每层节点进行加密, 若节点位于第i层, 则令该节点的位图作伪随机置换F(ski,bm), 其中ski= skf ⊕i. 对于叶子结点层级联的数组中每个元素编码-关键词, 将其加密生成一个tag ={tagfirst,tagsecond}: tagfirst= Encop(codekw) 其中Enc 为保序加密算法. tagsecond= Encver(kw||id1||id2||···||idk||hash(C1,C2,··· ,Ck)) 其中Enc为语义安全的对称加密算法, idi为包含kw 的文档标识符,Ci为idi对应Di密文. 输出加密后的OBBT 索引.

- Enc(D,k): 输入密钥k, 明文文档集D={D1,D2,··· ,Dm}, 加密每个文档Di得到密文文档集C={C1,C2,··· ,Cm}, 其中Ci=Enck(Di), Enc 为语义安全的对称加密算法.

- BuildIndex(sk,D): 输入密钥sk, 文档集D={D1,D2,··· ,Dm}以及密文文档对应的ID ={id1,id2,··· ,idm}.

(1) 从文档集D中提取出关键词字典WD={kw1,kw2,··· ,kwn}.

(2) 利用关键词字典WD按照3.1 节步骤(a),(b), (c), (d) 构建OBBT.

(3) 使用Index_Enc(sk,OBBT) 加密, 输出加密的OBBT 索引I.

- Trapdoor(sk,Q): 输入一个询问关键词Q和密钥sk. 首先, 按照步骤(b) 得到特征数组T′Q=[θ1′,··· ,?,··· ,θl′], 并对数组中每个数字进行如下置换θi=F(ski,θ′i) 其中ski= sk⊕i得到数组TQ= [θ1,··· ,?,···θl], 其中“?” 代表单字符通配符. 其次, 将通配符“?” 替换为a 和z, 利用编码算法分别计算出codemin,codemax, 并对编码值进行如下加密trcode= Encop(code) 其中code={codemin,codemax}, 输出陷门TQ,trcode.

- Search(TQ,I): 输入陷门TQ和索引I, 根据逐层匹配算法, 返回叶子节点所有的验证标签Tagsecond.

- Verify(sk,Tag): 输入密钥sk 和验证标签集Tagsecond.

(1) 利用skver解密tag(second,i)得到对应的kw,ids={id1||id2||···||idk},hash(C1,C2,··· ,Ck)

(2) 判断kw 与关键词Q是否匹配. 如果匹配, 将所有的ids 发送给云服务器; 如果不匹配, 结束此次验证.

(3) 云服务器返回所有的id-密文对(id1,Cid1),(id2,Cid2),··· ,(idk,Cidk).

(4) 把返回的密文进行hash 值校验, 验证hash(C1,C2,··· ,Ck)?=hash(Cid1,Cid2,··· ,Cidk) 如果相等输出1, 否则输出0.

注1 在验证阶段, 第一轮交互过程中, 验证kw 与关键词Q是否匹配, 如果匹配, 则说明服务器搜索结果是正确的, 否则认为搜索结果是错误的. 在第二轮交互过程中, 验证hash(C1,C2,··· ,Ck)?=hash(Cid1,Cid2,··· ,Cidk). 如果hash(C1,C2,··· ,Ck)/= hash(Cid1,Cid2,··· ,Cidk), 则说明至少有一个返回密文不正确的或返回结果不完整. 由此验证了服务器返回密文的正确性和完整性.

4 安全性分析

定理1 如果使用的对称密钥加密SKE 是PCPA 安全的,置换函数是伪随机置换,保序加密是ROPF安全的, 则无假阳性的可验证通配符可搜索加密方案是非适应性语义安全的.

证明: 如果对于PPT 敌手, 均存在一个多项式时间模拟算法Sim, 使得云服务器无法区分Real 的视图V和Sim 的视图V′, 那么云服务器就无法获得索引和数据集的其他任何信息.

给定一个查询历史的轨迹为T(H) ={AP,|·|},|·| 表示树的结构特性, 如树的高度和叶子结点的分布等. 模拟Real 的视图V=Encsk(D),Encsk(Ikw),Tr(Wk), 假设模拟器为Sim, Sim 具体工作步骤如下:

(4) 对于编码值对应的关键词密文, Sim 选择与关键词密文等长的随机串级联在数组中.由于密文是由语义安全的对称加密生成, 任意PPT 敌手无法区分Encsk(D) 与D′. 各层结构是由伪随机函数加密的, 叶子结点是由ROPF 保序加密函数和PCPA 安全的对称加密, 任意PPT 敌手无法区分I′与I. 陷门是由伪随机函数加密的, 因此Tr(Wk) 与Tr(W′k) 在多项式时间无法区分. 因此, 视图V(Encsk(D),I,Tr(Wk)) 与V′(D′,I′,Tr(W′k)) 在PPT 敌手下是计算不可区分的, 本文方案是非适应语义安全的.

5 功能与性能分析

本节将本文方案与Hu[17]的方案进行功能和性能对比, 通过仿真实验分别模拟用户和云服务器索引生成时间和搜索时间. 仿真实验是采用C++ 语言对方案性能进行测试, 运行环境是在AMD Ryzen 5 4600H CPU 3.00 GHz 和4 GB 内存的linux 系统上, 基于Boldyreva 的保序加密python 库.

由图3 可以看出, 本文方案相较于Hu 等人的方案, 存储复杂度几乎是不变的, 这是因为本文方案是预先建立的树形结构, 然后可以在树形结构中填充任意数量的关键词, 而Hu 的方案是倒排索引, 随关键词数量呈线性增长. 由图4 可以看出, 本文方案相较于Hu 等人的方案, 搜索效率极大提升, 且关键词数量的变化对本文方案搜索时间基本没有影响, 而Hu 等人方案的搜索时间随关键词数量线性增加, 这是由于我们构造了OBBT 索引, 而Hu 等人的方案为倒排索引. 由图5 可以看出, 本文方案相较于Hu 的方案, 需要更多的时间建立索引, 这是因为本文方案采用保序加密构造索引, 而保序加密本身效率较低且我们在实验时索引生成依赖于保序加密python 库, 但保序加密的使用使得本文方案实现了无假阳性, 且在加密数据库中索引建立的频率一般是远小于用户搜索频率的, 故这样的开销是可以接受的. 同时, 在表1 列出了与文献[14,16,17] 的功能对比, 相较于文献[14,16,17], 本文方案同时实现了通配符搜索、搜索结果无假阳性和搜索结果的可验证. 因此, 本方案能够很好地应用在云环境下.

表1 功能性对比Table 1 Functional comparison

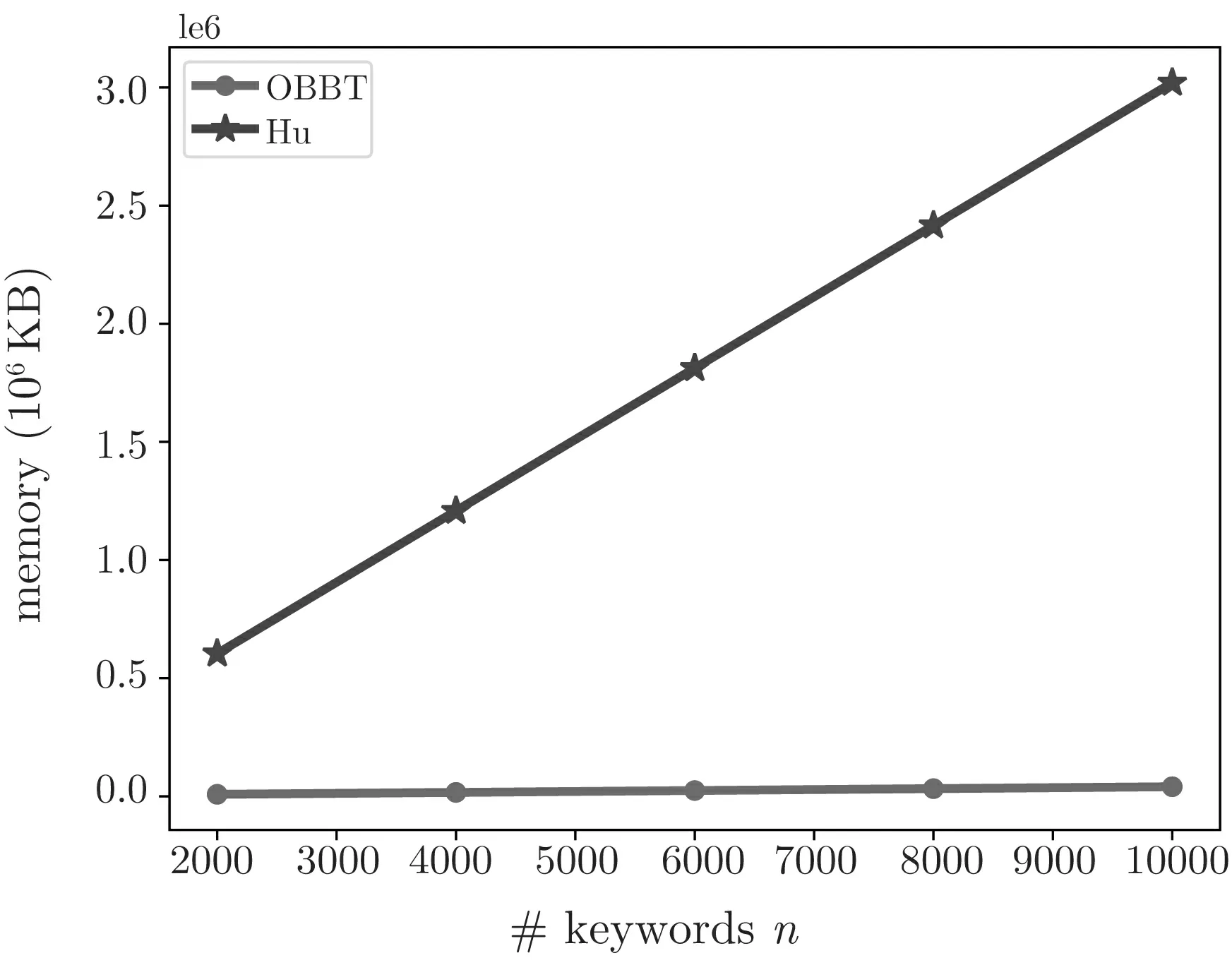
图3 存储开销Figure 3 Storage cost

图4 搜索时间Figure 4 Search time

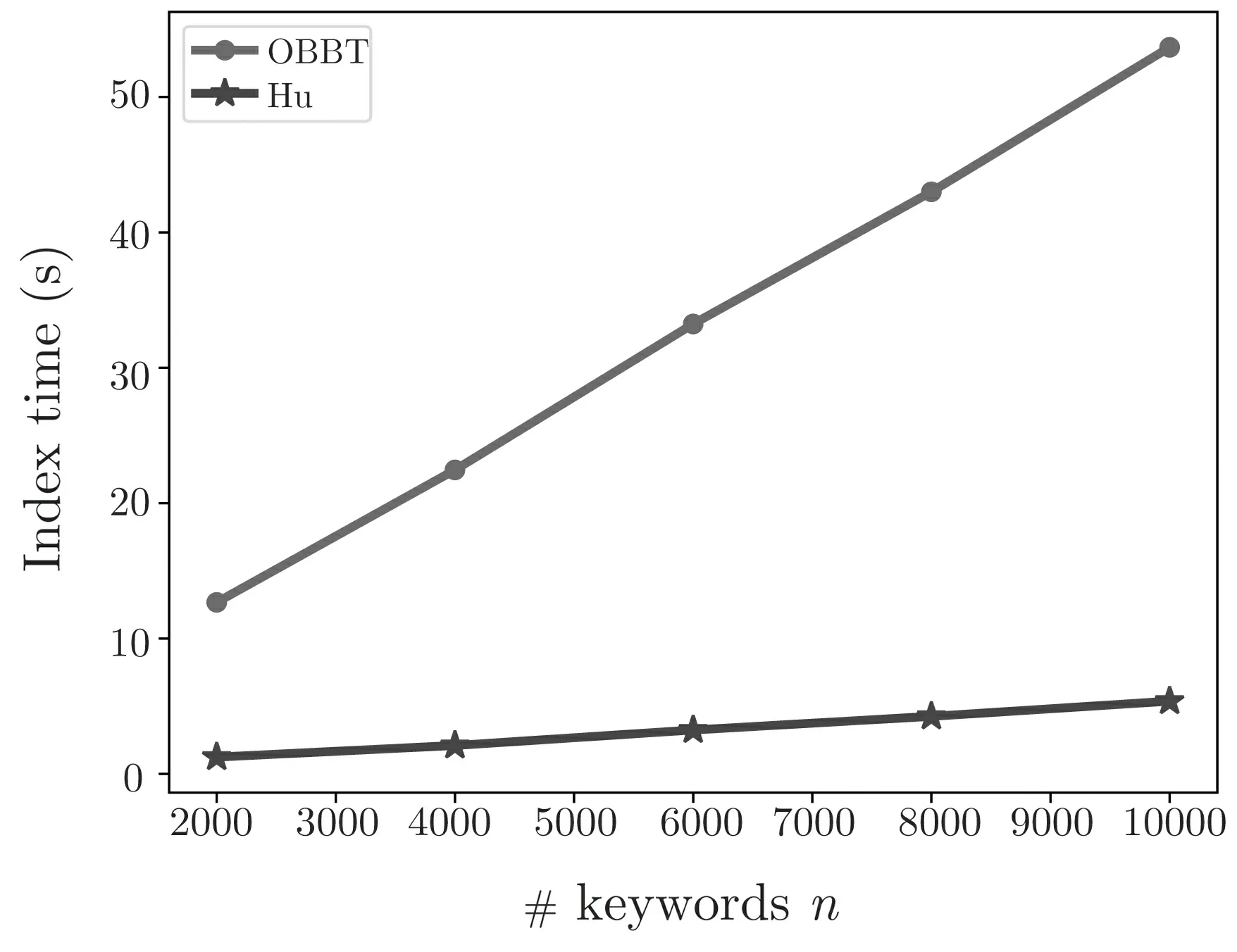
图5 索引构造时间Figure 5 Index construction time

6 结论

通配符可搜索加密的提出增加了用户的搜索体验. 针对现有通配符可搜索加密方案搜索结果存在假阳性且只考虑半诚实服务器模型的局限性, 本文提出了一个无假阳性的可验证单字符通配符搜索方案. 该方案将通配符搜索转化为范围搜索, 使用保序加密保证明文顺序与密文顺序的一致性, 并提出OBBT 索引提高其搜索效率. 所提出的方案搜索结果不存在假阳性, 支持对搜索结果正确性和完整性的验证, 且方案是非适应性语义安全的. 最后, 性能分析表明本文方案是高效的. 因此, 本文所提出的无假阳性的可验证通配符可搜索加密能够在实际中实现更好的应用.