一种在基于格的加密方案中搜索解密失败密文的方法*

陈昱帆, 陈辉焱, 张 珍, 张亚峰

北京电子科技学院, 北京 100070

1 引言

1.1 背景介绍

现代公钥密码的安全性大多数基于因子分解与离散对数问题. 然而, 由于量子计算机的发展, 世界对后量子密码的需求与日俱增. 格上的数学困难问题被认为在量子环境下仍然难解. 因此, 基于格的密码作为一种后量子密码而备受关注. 基于格的密码具有广泛的应用, 包括数字签名[1,2]、零知识证明[3,4]、公钥加密[5,6]与密钥封装等. 与其他后量子公钥加密方案相比, 基于格的公钥加密方案有着严格的可证明安全、灵活的安全等级、较小的计算量. 总之, 基于格的公钥加密方案是最好的后量子公钥加密方案之一. 美国国家安全局(NIST) 正在公开征集后量子公钥加密方案, 此时已经进行到了第三轮, 其中很多基于格的公钥加密方案入选了决赛, 例如saber[7]与kyber[8].

基于格的公钥加密方案与密钥封装方案都缺乏完美的正确性, 即使在加密过程中使用了正确的公钥与正确的加密方法, 仍然有可能发生加解密不一致. 本文中将加解密不一致的情况称为解密失败, 将导致解密失败的密文称为解密失败密文. 解密失败是由私钥与密文的共同作用所导致的结果, 解密失败密文会泄露私钥的信息, 进而影响方案的安全性. 由解密失败密文而推测私钥的攻击方法在本文中被称为解密失败攻击.

为了抵抗解密失败攻击, 大多数基于格的公钥加密方案会尽可能减少解密失败发生的概率. 然而降低解密失败概率必须调整方案参数, 导致方案的性能降低. 在NIST 公开征集的候选方案中, 解密失败概率普遍低于2-120. 部分方案会为了增加方案性能而选取较高的解密失败概率, 然后通过增加纠错码来降低解密失败概率[9]. 纠错码可以显著降低解密失败概率, 但是解密失败概率仍然不为0, 攻击者还是可以从解密失败密文中获得私钥信息.

因此, 研究如何在基于格的加密方案中搜索解密失败密文, 对基于格的加密方案的安全性有重要意义.

1.2 相关工作

在LWE 问题提出之前, 针对基于格的公钥加密方案的解密失败攻击就已经被提出. James 和Joux在文献[10] 中提出了针对NTRU 的解密失败攻击, 然后又对其加以拓展[11,12]. 之后, Fluhrer 提出了针对基于Ring-LWE 问题的方案的解密失败攻击[13], 然后Betu 在文献[14] 中对其进行了拓展.

然而, 上述所有的解密失败攻击都有一个使用前提: 攻击者必须使用特定的密文. 而文献[15] 与[16]中提出的FO 转换可以将选择明文安全的公钥加密方案转换为选择密文安全的密钥封装方案, 并且不允许攻击者随意创造密文. 因此, 上述的解密失败攻击都无法应用于FO 转换.

2018 年, D’Anvers 等人在文献[17] 中提出了一种在基于格的加密方案中搜索解密失败密文的方法,并将其命名为“failure boosting”. 此攻击方法可以应用于所有的基于LWE/LWR 问题的公钥加密与密钥封装方案. 之后在2019 年, D’Anvers 等人在文献[18] 中对“failure boosting” 进行了进一步的分析与拓展. 同年, D’Anvers 等人改进了“failure boosting”, 提出了一种新的搜索解密失败密文的方法, 并将其命名为“directional failure boosting”[19].与此同时, Guo 等人提出了两种分别针对LAC[20]和SS-NTRUPKE[21]的解密失败攻击. 2020 年, Bindel 和Schank 证明了没有产生解密失败的密文也可以用于解密失败攻击[22].

尽管解密失败攻击已得到了有效的优化, 但是仍然需要很高的计算量, 因此上述方法的有效性难以直接通过实验来验证.

1.3 本文贡献

D’Anvers 等人提出的“directional failure boosting” 有着一个不合理的假设: 在“directional failure boosting” 中, D’Anvers 等人将私钥设定为一个多项式向量,并且将私钥的l2-模设定为私钥中的多项式的系数所组成的向量的l2-模. D’Anvers 等人假设私钥中所有的系数在方案给定的分布中随机选取, 并且在选取时相互独立, 进而得出私钥的l2-模的分布函数.

在单密钥攻击的前提下, 私钥的l2-模是一个固定的数值. 仅仅利用私钥中系数的分布很难准确推测出私钥的l2-模. 本文中提出了一种新的搜索解密失败密文的方法, 该方法从解密失败密文的数量与解密查询的次数中提取出私钥的信息, 然后得出一个新的私钥的l2-模的分布函数, 进而改进了“directional failure boosting”. 第4 节中的实验表明, 本文提出的方法比“directional failure boosting” 更加有效.

2 基础知识

2.1 格密码基础知识

2.1.1 数学知识

2.1.2 LWE 问题

同时还存在着Mod/Ring-LWE 问题. 将上述LWE 问题中的Zq更改为Rq来获得Rq上的矩阵和向量. 如果上述维度l不等于1, 那么就形成了Mod-LWE 问题; 如果l等于1, 就形成了Ring-LWE 问题.

2.1.3 基于LWE 问题的公钥加密方案

D’Anvers 等在文献[17,19] 中总结出基于LWE 问题的公钥加密方案的通用构架, 本文将简要描述.

公钥加密方案包括密钥生成算法、加密算法和解密算法. 下面, Gen 代表密钥生成算法, Enc 代表加密算法, Dec 代表解密算法. 定义M ⊆Rq代表明文空间. 明文中的多项式的系数从{0,1}中选取. 下述Enc 中的r是一段比特串.x ←χ(Rq;r) 代表将r看做随机选取而得的比特串, 并利用r在分布χ(Rq)中选取x.

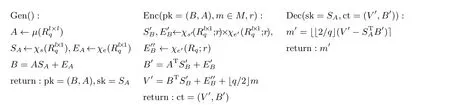
在文献[19] 中, D’Anvers 等人定义χs、χe、χs′、χe′为四个相同的期望值为0 的高斯分布, 并且分布的方差很小. 本文中假定上述四个分布都是以零为中心的对称离散分布, 并且取值空间很小.

很多基于格的公钥加密方案都有着较高的带宽. 所有在实际应用过程中, 很多加密方案都会对密文进行压缩. 而压缩会产生一个额外的误差, 这个误差会影响解密失败. 在文献[19] 中, D’Anvers 等人仅仅考虑上述模型下的加密方案, 没有考虑密文的压缩. 本文中的方案作为文献[19] 中“diectional failure boosting” 的改进, 也不考虑上述密文压缩的问题.

为了将选择明文安全的公钥加密方案转换为选择密文安全的密钥封装方案, 很多方案设计者会选择FO 转换[15,16]. 一个密钥封装方案包括封装算法和拆封算法. 本文中将封装算法记为Encaps, 将拆封算法记为Decaps. 下述H() 与G() 代表在密钥封装方案中所使用的两个哈希方程, 其输入可以是任意数值,输出是一段可以近似看作随机的比特串.

为了更方便的表达解密失败, 需要定义出下述多项式和向量.

定义1

然后, 解密出的明文m′可以表示如下:

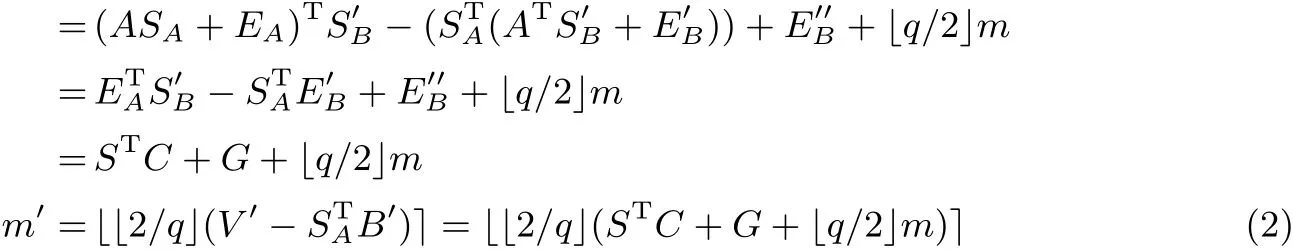
在上述加密方案中, 本文设定qt=/4」. 可以发现,‖STC+G‖∞＞qt与m′/=m可以近似看作等价,所以, 可以认为‖STC+G‖∞＞qt时解密失败才会发生.

根据公式(1), 可以发现:

因为S和C都是由2l个n-1 级多项式组成的向量, 所以每个STC中的系数都是由2l*n个数值相加得到.G中的系数是从χe′中选取而来. 在本文的设定中,χs、χe、χs′、χe′都是以0 为中心的离散分布, 并且取值空间很小. 因此,G中的系数的绝对值与STC中的系数的绝对值比起来, 非常小,P(‖STC+G‖∞＞qt)≈P(‖STC‖∞＞qt). 在文献[19] 中, D’Anvers 等人也直接忽视了G的影响.P(‖STC‖∞＞qt) 可以写作:

本文中, 将‖STC‖∞＞qt描述为STC产生了解密失败. 如果STC中的某个系数的绝对值大于qt,本文中描述为这个系数产生了解密失败.

2.1.4 选择密文安全

定义κ代表密钥K的选择空间. 一个攻击者A攻击密钥封装方案的优势由下述公式定义. 如果该优势可以忽略, 那么密钥封装方案可以被认为选择密文安全.

2.2 D’Anvers 的方法

本小节将简述D’Anvers 的“failure boosting” 和“directional failure boosting” 两种方法. 对于详细细节与原理, 请参阅文献[17,19].

在文献[17] 中, D’Anvers 等人提出了一种获得解密失败密文的方法, 并将其命名为“failure boosting”. 然后在文献[19] 中, D’Anvers 等人又提出了一种“failure boosting” 的改进, 并将其命名为“directional failure boosting”. 两种方法的大致思路如下:

第一步: 获得一个密文(C,G), 然后计算出该密文产生解密失败的概率, 如果该概率大于一定数值, 就将该密文选为“弱密文”.

第二步: 获得了一定量的弱密文之后, 将所有的弱密文输入解密查询, 意图获得解密失败.

两种方法的差别在于: 对于给定密文, 如何计算该密文的解密失败概率. 下面将简要介绍两种方法的差别.

2.2.1 failure boosting

“failure boosting” 可以应用于所有基于LWE/LWR 问题的加密方案.

对于给定的C和G, 假定S中的系数从分布χs和χe中随机选取且相互独立. 因此,STC中的每个系数都可以看作由2l*n个相互独立的数值相加而来, 进而都可以看作从同一个高斯分布中选取. 且STC中的系数之间可以近似看做相互独立.

D’Anvers 等人通过下述公式计算出高斯分布的方差. 设Cij代表C中第i+1 个多项式的Xj的系数.STCi代表STC中Xi的系数. var(STCi) 代表STCi的分布的方差. 因为χs和χe都以0 为中心,所以STCi的分布的期望值为0.

将解密失败记作事件F. 然后用下述公式计算给定密文(C,G) 的解密失败概率.

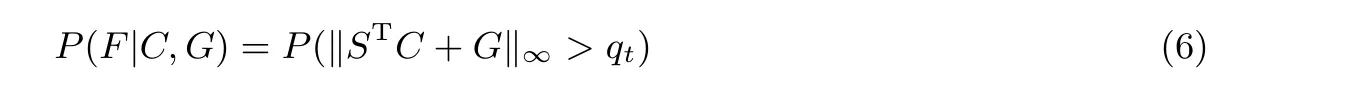
2.2.2 directional failure boosting

尽管“directional failure boosting” 是“failure boosting” 的一个改进, 但“directional failure boosting” 有两个局限性:

在单目标攻击的情况下,‖S‖2是一个固定的数值. D’Anvers 等人缺少了对‖S‖2的合理预测, 而是直接假设其在相应的分布中随机选取. 这样很显然会影响弱密文筛选的准确性.

2.2.3 恢复私钥

仅仅获得解密失败密文不会影响方案的准确性, 但是解密失败密文可以应用于某些私钥恢复攻击, 如文献[17,21] 中的方法.

2.3 改进“directional failure boosting”

根据第2.2.2 节所述, “directional failure boosting” 缺少了对‖S‖2的预测. 并且在“directional failure boosting” 使用之前, 需要先使用“failure boosting” 来获得至少一个解密失败密文.

本文中假定攻击者首先使用“failure boosting” 进行了多次解密查询, 并且获得了至少一个解密失败密文. 然后本文将详细阐述如何应用“failure boosting” 中的解密查询次数与解密失败密文个数来预测‖S‖2.

2.4 方法简介

由于本文中的方法是针对“directional failure boosting” 的一个提升, 所以本文中的方法也仅仅可以应用于单目标攻击. 在单目标攻击的情况下, 本文将攻击者要攻击的私钥称为目标私钥.

根据公式(6), 可以发现: 对于一个特定的私钥, 解密失败不仅仅取决于输入查询的密文, 还取决于该私钥. 假设输入解密查询的密文从某个特定的分布中随机选择, 那么就可以从解密失败概率中获得私钥的信息.

然而, 上述思路存在如下两个需要解决的问题:

P1: 只有弱密文才能输入解密查询. 想要实现上述思路, 就必须计算出弱密文的分布.

P2: 对于某个特定的目标私钥, 攻击者并不知道该私钥的解密失败概率.

为了解决上述两个问题,本文将注意力集中于“failure boosting”.下面将介绍如何利用“failure boosting” 来解决上述两个问题.

D’Anvers 等人在“failure boosting” 将弱密文定义如下: 假设私钥中的系数都是从χs或χe中随机选取且相互独立, 对于给定密文通过公式(6) 计算出解密失败概率, 如果解密失败概率大于一定数值, 就将其选择为弱密文. 本文中将弱密文中的系数所服从的分布称为“弱密文分布”.

利用“failure boosting” 中弱密文的概念, 通过贝叶斯公式可以计算出“failure boosting” 中的弱密文分布. 然后假设输入解密查询的弱密文的系数都是从弱密文分布中随机选取, 就解决了问题P1. 在2.5 节中, 将会对这一步骤的原理进行详细的阐述.

在获得“failure boosting” 的弱密文分布之后, 本文中假设攻击者使用“failure boosting” 针对目标私钥进行了数次解密查询并且获得了至少一个解密失败密文. 利用解密查询次数以及所获得的解密失败密文的个数, 可以推测出目标私钥的解密失败概率, 进而解决问题P2.

综上, 在利用了“failure boosting” 获得了至少一个解密失败密文之后, 可以利用解密失败密文的个数与解密查询的次数来推测出私钥的信息.

在解决了问题P1 与P2 之后, 将注意力集中到“directional failure boosting”. 如2.2.2 节中所述, 在“directional failure boosting” 使用之前, 必须首先使用“failure boosting” 来获得至少一个解密失败密文; 并且“directional failure boosting” 中缺少对‖S‖2的合理推测. 因此, 在使用“failure boosting” 获得了至少一个解密失败密文之后, 攻击者可以利用解密查询次数与解密失败密文的个数来推测出私钥的信息, 并将其转换为‖S‖2的信息. 然后攻击者就可以通过得出的‖S‖2的信息来改进“directional failure boosting”.

本文中将上述方法的具体实现分为四个步骤:

第一步: 计算出“failure boosting” 中的弱密文分布. 这一步的目的是解决问题P1. 在计算出之后, 可以假设“failure boosting” 中的弱密文的系数都是从其弱密文分布中随机选取.

第二步: 计算出目标私钥的解密失败概率的概率密度函数. 这一步的目的是解决问题P2. 如前文所述, 利用“failure boosting” 的解密查询次数与解密失败密文个数, 可以推测出目标私钥的解密失败概率的概率密度函数.

第三步: 解决了问题P1 与P2 之后, 可以获得目标私钥的部分信息. 然后这一步的目的就是将私钥的信息转化为‖S‖2的分布函数.

第四步: 在获得了‖S‖2的分布函数之后, 使用其来改进“directional failure boosting”.

2.5 第一步: 计算弱密文分布

本小节的目的是获得“failure boosting” 中的弱密文分布. 在获得了弱密文分布之后, 就可以假设“failure boosting” 中输入解密查询的弱密文的系数都是弱密文分布中随机选取, 进而解决问题P1.

在本小节的最后额外说明, 在S固定, 并且C中的系数在弱密文分布中随机选取的情况下, 由于C中的各个系数之间的协方差为0, 所以STC中的系数可以近似看作高斯分布.

首先将“failure boosting” 中的弱密文的选择标准进行等价转换.

在本小节中假设“failure boosting” 中的弱密文的选择标准是解密失败概率大于Pt. 已知对于给定的C和G, 在“failure boosting” 中将解密失败概率表示为P(‖STC+G‖∞＞qt). 在本文的设定中,G的影响非常有限, 可以假设P(‖STC+G‖∞＞qt)≈P(‖STC‖∞＞qt), 文献[19] 中也做出了同样的假设.

在本文的设定中,S和C都是2l维的多项式向量, 所以STC只包含一个多项式. 在“failure boosting” 中假设STC中的n个系数都是从相同的高斯分布中随机选取并且相互独立. D’Anvers 在文献[18] 中说明上述假设在没有纠错码的情况下是合理的. 由此, 可以得到: 1-P(‖STC‖∞＞qt)≈(1-P(|STCi|＞qt))n. 设定数值P′t, 令其满足1-Pt=(1-P′t)n.

在上述公式中共有2l*n项元素, 并且所有元素之间相互独立. 将前2l*n-1 项元素相加所得到的和近似看作一个高斯分布, 记为分布N′. 由于var(χs) 和var(χe) 都是已知的数值, 并且χe′和χs′已知,所以分布N′的期望值和方差可以通过计算轻松得到.

需要注意, 当χe′与χs′都是高斯分布且相同, 并且var(χs)=var(χe) 的时候, 也可以将N′看作是一个卡方分布.

将密文被选为弱密文记为事件Fw.s′0在弱密文中的分布可以被下述公式计算出:

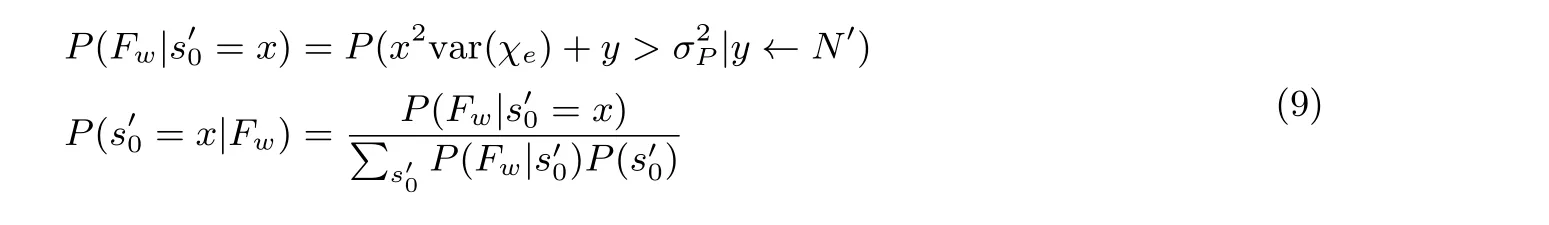
将弱密文中的s′i和e′i的分布分别记作χs′-new、χe′-new.

显然, 所有的s′i都服从和s′0相同的分布. 若延续文献[19] 中的参数设定, 可以得到相同的χs′-new和χe′-new. 而当χs和χe不同的时候, 可以用相同的方法计算出χe′-new.

至此, 获得了弱密文分布, 解决了问题P1.

需要注意的是, 在C被选为弱密文的前提下, 其中的系数显然已经不满足相互独立.

然而, 根据2.1.3 节中所述,χs′和χe′都是以0 为中心的对称分布. 通过公式(9) 可以得到χs′-new和χe′-new也都是以0 为中心的对称分布. 根据协方差公式cov(a,b) =E(ab)-E(a)E(b), 可以得到弱密文C中的所有系数之间的协方差为0.

因此, 当S是一个固定的私钥,C中的系数从弱密文分布中选取的情况下,STC中的每个系数都可以近似地看作由2l*n个相互独立的数值相加而来, 然后近似地看作一个高斯分布. 显然该高斯分布的期望值仍然为0, 参考公式(5), 该高斯分布的方差为‖EA‖22var(χs′-new)+‖SA‖22var(χe′-new).

2.6 第二步: 计算解密失败概率的概率密度函数

首先获得“failure boosting” 中的γ与解密失败概率之间的一一映射.

在S为目标私钥、C中的系数在弱密文分布中选取的前提下,STC中每个系数的解密失败概率可以表示为:

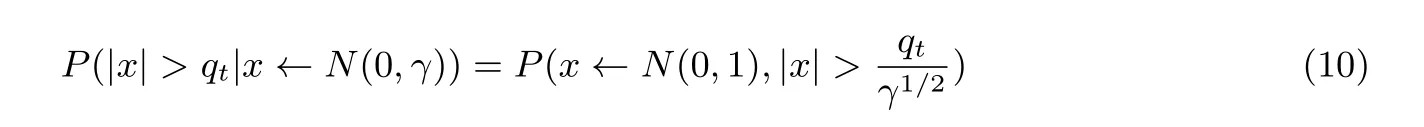
根据上述公式, 可以得知: 存在一个STC中每个系数的解密失败概率与γ之间的一一映射. 进而知道存在一个γ与STC的解密失败概率的一一映射. 对于固定的γ, 假设STC中的系数之间相互独立, 设相应的STC的解密失败概率为Pγ. 映射方程可以表示为:

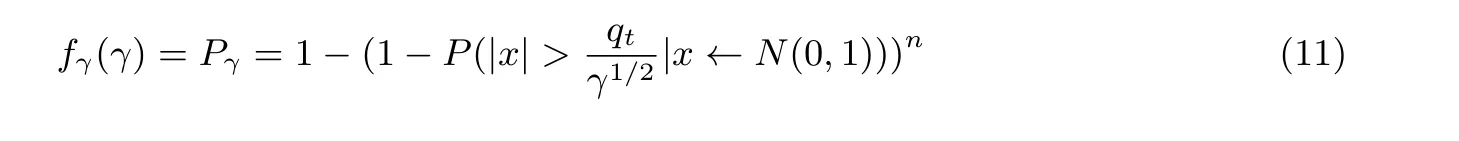
然后本小节的剩余目的就是通过解密查询次数与解密失败密文个数来获得一个γ的概率密度函数.

假设私钥S中的系数都是从分布χs和χe中选取而来. 由于γ共由2l*n个相互独立的数值相加得到, 所以可以将γ近似的看作服从高斯分布, 记为Nγ.

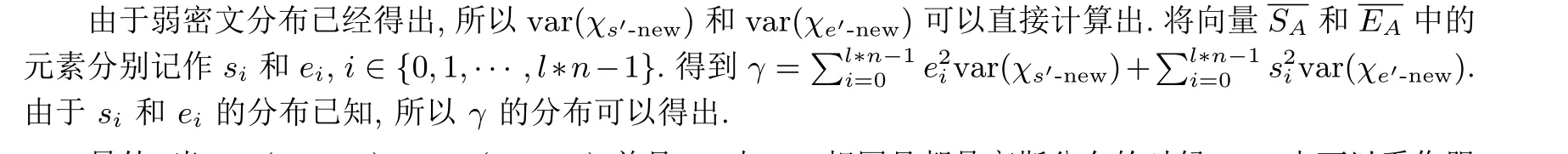
另外, 当var(χs′-new) = var(χe′-new) 并且χs与χe相同且都是高斯分布的时候,Nγ也可以看作服从卡方分布.

至此, 获得了γ的概率密度函数. 最后, 利用贝叶斯公式, 带入解密查询次数与解密失败密文的个数,可以获得γ的新的概率密度函数, 记为fγnew. 假设“failure boosting” 中进行了k次解密查询并且获得了k1个解密失败密文, 可以得到:

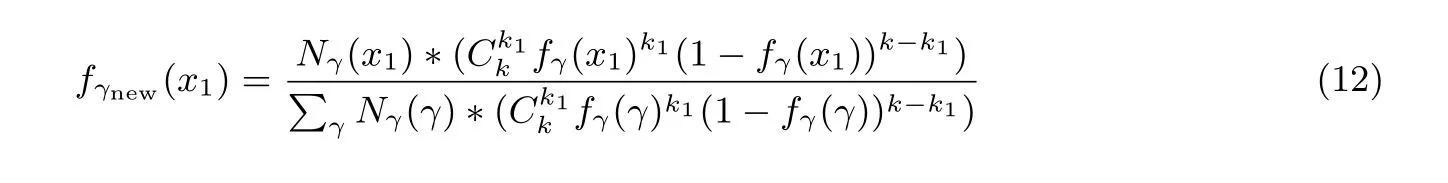
由于上式的分母难以有效求出原函数, 所以将其当作离散的函数, 并假设其取值为整数且间隔为1. 由于在实际的加密方案中S中系数的分布是离散的, 所以γ的分布本就是离散的, 上述假设相当于将间隔相近的离散数值当作同一个数值考虑.

需要注意的是在实际应用中, 最有效的攻击方法是利用“failure boosting” 获得了一个解密失败密文之后立刻转而使用“directional failure boosting”, 所以在大部分情况下k1=1.

2.7 第三步: 获得私钥信息

现在, 问题P1 和P2 都已经解决, 可以开始提取目标私钥的信息.

本小节中, 将会详细解释如何从现有信息中提取出目标私钥的信息, 然后将私钥的信息转化为‖S‖22的分布函数.

2.7.1 提取私钥信息

第一个目的是利用fγnew来获得目标私钥中的系数的信息.

对于一个固定的目标私钥S, 假设密文C在弱密文分布中随机选取. 如2.5 节所述,STC中的参数的分布的方差是γ, 可以写作:

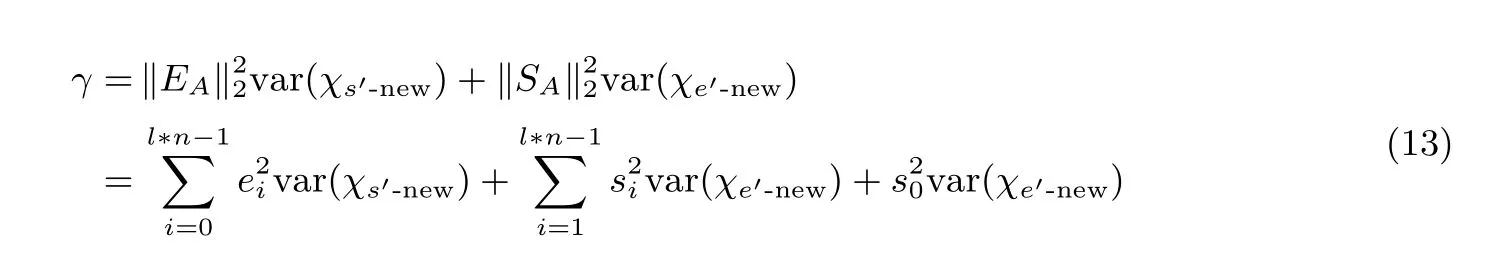
在没有fγnew的情况下, 已知si和ei在选取时相互独立. 所以上述公式的前2l*n-1 项可以看作一个高斯分布, 将其记为Nr.Nr的方差和期望值可以像Nγ一样被计算出来.

需要注意, 当设定Nγ为卡方分布的时候,Nr也必须设为卡方分布.

在2.6 节, 关于γ的新的概率密度函数已经得到.s20的分布可以通过χs得到. 然后应用贝叶斯公式将fγnew代入, 就可以得到一个新的s20的分布, 将其记为χs2-new:

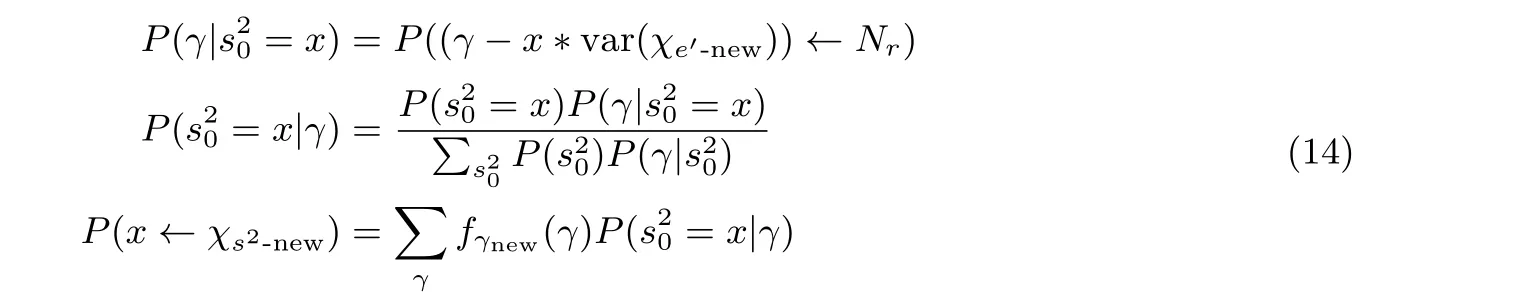
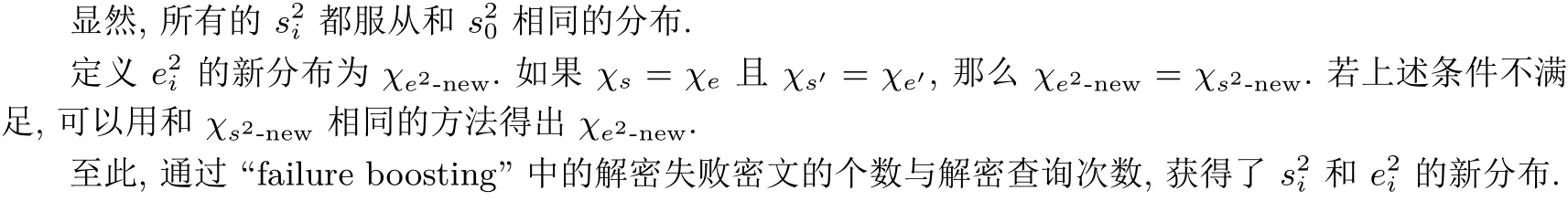
2.7.2 获得‖S‖2的分布函数

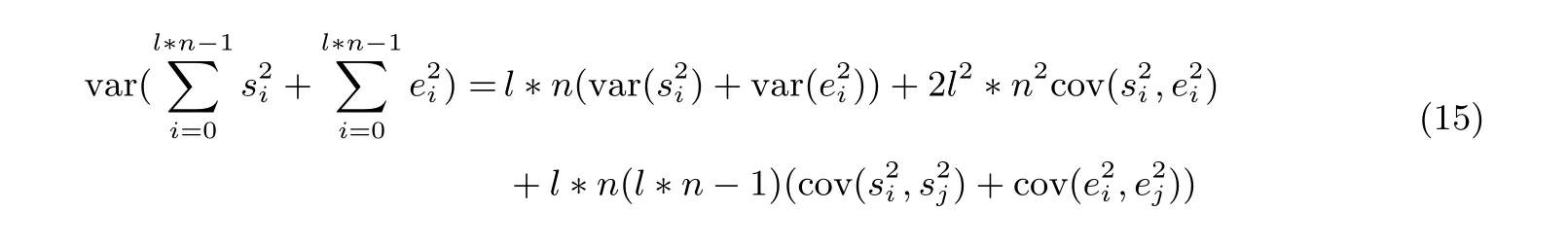
与公式(13) 相似, 为了获得协方差, 将s20+s21记作t. 下一步的目的就是通过γ的新分布获得t的新分布.

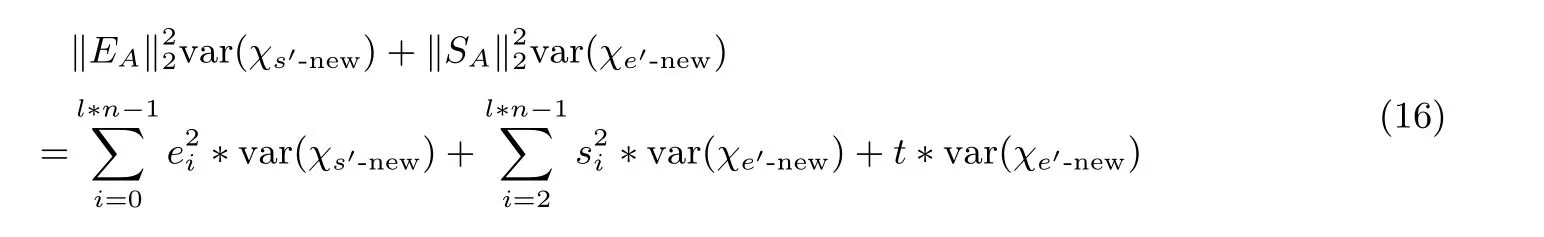
首先写出在没有fγnew的情况下,γ的表达式:知, 所以分布N′r的期望值和方差可以通过和Nr类似的方法得到.

在没有任何私钥信息的情况下,t的分布可以通过χs得到. 然后通过贝叶斯公式和γ的新分布, 可以获得t的新的分布:

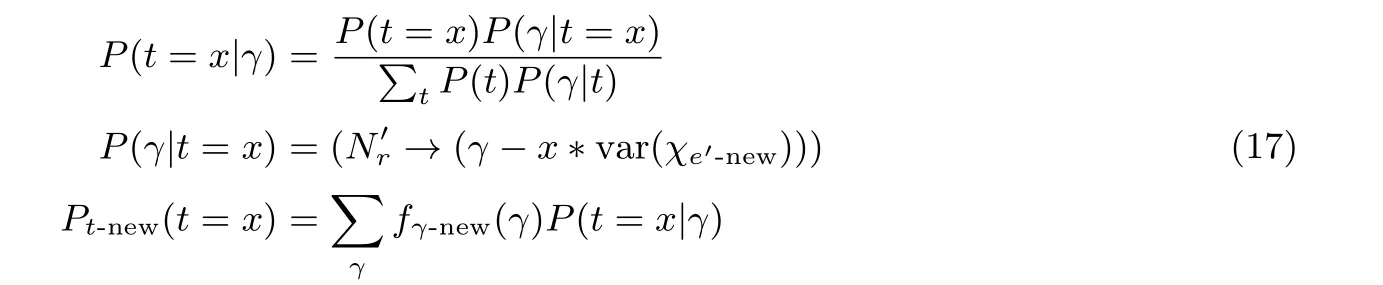
2.8 第四步: 提升“directional failure boosting”

在2.7 节的最后, 获得了‖S‖2的分布. 将‖S‖2的分布函数代入公式(7), 就可以获得一个更加有效的“directional failure boosting”.

3 讨论

3.1 本文中的改进方法的开销

对于大多数加密方案来说,私钥S和密文C中的系数的选取范围非常有限.在文献[19]中,D’Anvers等人以saber[7]和kybe[8]作为参考来选择参数. 在saber[7]和kybe[8]中,S和C的系数的选取范围都不超过10 个整数.

但是有些加密方案中的S和C的系数选取范围很大. 例如SS-NTRU-PKE 中,S和C的系数是从期望值为0、标准差为724 的离散高斯分布中选取而来. 而过大的选取范围会显著影响本文中的方法的计算开销. 为了应对上述情况, 可以将S中的系数的选取范围分割为数个区间, 然后以区间为单位来进行操作. 另外, 当S和C中的系数的选取范围增大时, 为了保证解密失败概率很低,q也必须相应增大. 如SS-NTRU-PKE 中,q=230+213+1. 显然,qt会随着q的增大而增大, 进而‖STC‖∞＞qt中的所有系数都会很大. 所以当本文中的改进方法在实际应用过程中计算开销过大时, 只需将‖STC‖∞＞qt中的所有系数都等比例缩小然后取整数, 就可以显著降低计算开销.

由于本文中的改进方法是文献[19] 中的“directional failure boosting” 的改进, 所以在本节中, 假设S和C中的系数的选取范围都是非常有限的整数集合.

本文中的改进方法的第一步仅仅需要对C的系数的选取空间进行遍历, 其计算开销可以直接忽略.

本文中的改进方法的第二步的计算开销主要集中于γ的取值空间的遍历. 将γ的所有可能的离散值的个数记为|γ|. 根据文献[19] 中的参数选取,|γ|≈217. 在文献[19] 中, D’Anvers 等人对使用“failure boosting” 获得第一个解密失败密文所需要的解密查询次数进行了预估, 认为需要2102.21次解密查询. 本文中假设对于给定数值x, 计算x2102.21需要27次运算. 由于第二步对γ的每个取值的遍历中, 指数运算的开销占据了绝大部分, 所以本文中的改进方法的第二步的计算开销大约为224. 由于γ的新的分布函数在之后数次用到, 所以可以消耗|γ| 大小的存储, 用来储存γ的新的分布.

在本文的改进方法的第三步中, 总计算开销大约为|γ|*|χs|2*22. 根据文献[19] 中的参数选取, 大约为224. 另外, 如果在具体应用时,χs/=χe或χs′/=χe′, 那么第三步的计算开销就扩大为4 倍.

如2.6 节所述, 本文中假设γ的取值范围是离散且间隔为1 的. 如果在具体应用的时候计算开销不可接受, 也可以通过改变假设中γ的离散间隔来减少计算开销.

在文献[19] 中, D’Anvers 等人预测: 在解密查询次数没有限制的情况下, 以1-e-1的概率获得第二个解密失败密文大约需要2110的计算开销. 根据文献[19] 中的参数选取, 本文中的方法所造成的额外的计算开销仅仅需要230, 相较之下可以直接忽略.

3.2 与文献[19] 中“directional failure boosting” 的对比

本文中所提出的方法是对“directional failure boosting” 的一个改进, 所以本小节中将本文的方法与“directional failure boosting” 进行对比.

本文中的方法与“directional failure boosting” 的差异在于本文中的方法增加了额外的步骤. 如果“directional failure boosting” 的假设足够理想, 那么本文中的方法不会带来任何提升. 但是如前文所述,“directional failure boosting” 缺少对‖S‖2的预测, 进而导致弱密文的选择不够合理. 本文的方法通过增加对‖S‖2的预测来使弱密文的选择更加合理, 进而可以使“directional failure boosting” 更加有效.

另外, 本文中的方法有着比“directional failure boosting” 更加宽松的要求. 例如, 本文中的方法不要求χs、χe、χs′和χe′相同, 但是“directional failure boosting” 要求. 所以, 在某些情况下, 即使“directional failure boosting” 不可用, 攻击者仍然可以用本文中的方法来获得私钥的信息.

4 实验验证本文中的方法所带来的提升

尽管我们认为本文中的方法可以为“directional failure boosting” 带来提升, 但是难以从理论上量化具体的提升数值. 所以本节中, 将会用实验来量化本文中的方法所带来的提升.

本文中的方法与“directional failure boosting” 的差别在于本文中的方法对‖S‖2做了额外的预测.而“directional failure boosting” 则假设χs、χe、χs′和χe′都是相同的高斯分布, 然后认为‖S‖22在相应的卡方分布中随机选取. 所以本节中, 将本文中的方法所获得的‖S‖22的分布函数与“directional failure boosting” 中所使用的卡方分布进行对比, 进而验证本文中的方法所带来的提升.

4.1 参数选取与假设

为了更加方便与“directional failure boosting” 进对比, 本文的实验的参数选取会尽可能的满足“directional failure boosting” 的要求. 在文献[19] 中, D’Anvers 等人假设χs和χe是相同的离散高斯分布. 实验中我们参考了kyber768[8]的方法, 用中心二项分布来代替高斯分布, 生成私钥. 具体的参数选取如下: 设定l=3、n=256, 对于每一个si, 采用下述方法生成. 而ei的生成方法与si相同.

在“directional failure boosting” 中, D’Anvers 等人假设χe和χs都是高斯分布, 然后利用卡方分布得到‖S‖的分布, 进而得到‖S‖2的分布函数. 需要注意的是, 由于理想的高斯分布难以实现, 用中心二项分布来代替高斯分布是一种非常常见的方法, 在很多的加密方案中都被使用.

本文中的方法的使用前提是攻击者已经使用“failure boosting” 获得至少一个解密失败密文. 但是在实际应用过程中, 使用“failure boosting” 获得一个解密失败密文需要很大的计算开销, 难以实现. 所以本文根据一些假设来调整实验.

已知在“failure boosting” 中, 只有弱密文会被输入解密查询. 在2.5 节中, 攻击者可以获得弱密文分布. 并且在本文的方法的第二步和第三步中, 仅仅用到了弱密文分布的方差, 没有用到具体的弱密文.

所以, 实验中做出如下假设:

假设 1 实验中不再设定 “failure boosting” 中弱密文的选择标准, 直接设定 var(χs′-new) =var(χe′-new)=3.

由于弱密文的选取标准可以由攻击者随意指定, 且弱密文分布的方差由弱密文的选取标准而确定, 所以, 在实验中, 弱密文分布的方差var(χs′-new) 和var(χe′-new) 也可以由攻击者任意指定. 上述假设1 可以认为合理.

通过公式(10) 和(11), 可以计算出给定私钥在“failure boosting” 中的解密失败概率. 然后, 在区间(0,1) 之间的均匀分布中任意选取一个小数. 通过这个小数, 可以模拟一次解密查询:

如果这个小数的数值小于等于给定私钥的解密失败概率, 那么就认为进行了一次解密查询并且发生了一次解密失败. 否则, 认为进行了一次解密查询但没有发生解密失败.

通过上述方法, 对于给定私钥, 可以在“failure boosting” 中获得一个相对合理的解密查询次数和解密失败密文个数. 所以实验中做出如下假设:

假设2 实验中认为公式(10) 和(11) 是正确的. 然后通过在区间(0,1) 之间的均匀分布中任意选取一个小数来模拟一次解密查询. 如果这个小数的数值小于等于给定私钥的解密失败概率, 那么就认为进行了一次解密查询并且发生了一次解密失败. 否则, 认为进行了一次解密查询但没有发生解密失败.

公式(10)和(11)的正确性依赖于以下两点: 在S固定、C中的系数从弱密文分布中随机选取的前提下,

(1) 将STC中的系数看做从高斯分布中随机选取.

(2) 假设STC中的系数相互独立.

第(1) 点在2.5 节末尾进行了说明, 第(2) 点在文献[18] 中得到了证明.

在公式(10) 和(11) 正确的前提下, 通过公式计算出的给定私钥的解密失败概率是合理的, 所以利用假设2 获得的解密查询次数与解密失败密文个数也是合理的. 所以假设2 可以被认为合理.

通过上述两个假设, 可以在试验中直接获得解密查询次数和解密失败密文个数, 而不需要真正的解密查询. 然后, 为了进一步减少实验的计算开销, 设定qt=300.

最后, 由于最有效的攻击方法是在使用“failure boosting” 获得一个解密失败密文之后立刻转而使用“directional failure boosting”, 所以在公式(12) 中, 设k1=1.

4.2 本文中获得的分布的准确度

在实验中, 我们首先扮演挑战者, 生成私钥, 然后使用4.1 节中的方法模拟解密查询, 直到获得一次解密失败. 最后将解密查询次数与解密失败密文个数发送给攻击者.

然后扮演攻击者, 使用本文中的方法获得一个‖S‖22的分布.

最后, 为了量化本文中的方法获得的‖S‖22分布的准确度, 我们将目标私钥的‖S‖22分别带入到本文中的方法获得的概率密度函数、“directional failure boosting” 所使用的卡方分布的概率密度函数之中, 然后进行对比.

基于以上假设, 我们在matlab2020b 中进行了实验.

4.3 本文中的方法所带来的提升

在获得了‖S‖2的分布之后, 实验的目的就是量化本文中的‖S‖2的分布能为“directional failure boosting” 带来多大的提升. 然而, 由于客观条件的限制, 结果难以直接通过实验验证.

图1 实验中adv1 的数值Figure 1 adv1 in experiment

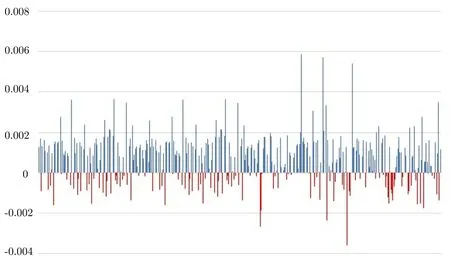
图2 实验中adv2 的数值Figure 2 adv2 in experiment

图3 实验中adv3 的数值Figure 3 adv3 in experiment

4.3.1 “directional failure boosting” 的效率

从上述公式可以看出, cos(θSE)cos(θC(r)E)+sin(θSE)sin(θC(r)E)cos(t) 可以看作是cos(θSC(r)) 的一个预测. 所以实验中做出下列假设:

假设3 对于一个给定的密文C,假设对于所有的r ∈{0,1,··· ,2n-1},攻击者可以获得cos(θSC(r)).

需要注意,在“directional failure boosting”中,攻击者仅仅可以获得一个cos(θSC(r))的分布,而不是cos(θSC(r)). 只有当该分布足够合理的时候, 上述假设才可以被认为合理. 在文献[19] 中, D’Anvers 等人认为“directional failure boosting” 中cos(θSC(r)) 的分布是合理的, 然后利用该分布来预测“directional failure boosting”的攻击效率.并且D’Anvers 等人认为随着解密失败密文个数的增加,“directional failure boosting” 可以获得近乎准确的cos(θSC(r)) 的值. 另外, 当攻击者可以获得cos(θSC(r)) 时, 弱密文的筛选的准确程度将仅仅取决于‖S‖2的分布的准确程度,所以假设3 可以使实验很好的反映本文中获得的‖S‖2的分布在实际中所带来的提升. 所以, 假设3 在本实验中可以被认为是合理的.

接下来将会解释“directional failure boosting” 如何在假设3 成立的条件下运行. 对于一个给定的密文C, 在cos(θSC(r)) 的情况下, 公式(7) 可以写作:

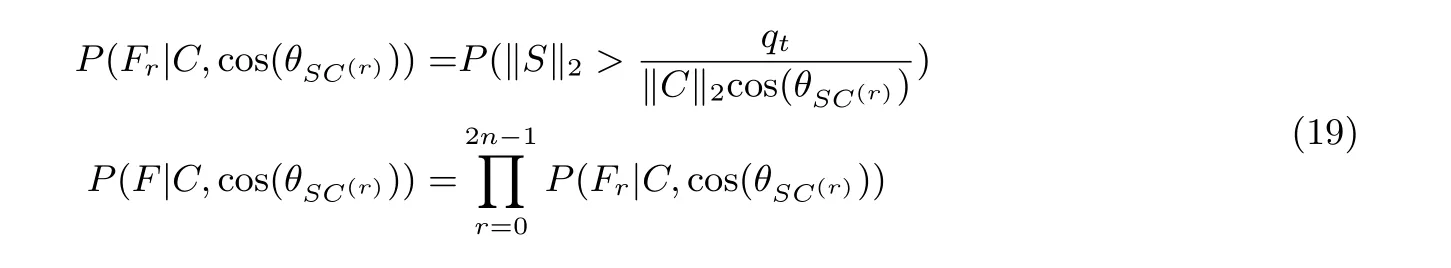
下面将解释, 对于一个Pt, 如何获得ωPt和QPt.

如文献[18] 中所述, 在‖S‖2和‖C‖2确定的前提下,STC中的系数然可以被看作相互独立. 所以对于r ∈{0,1,··· ,n-1},θSC(r)之间可以看作相互独立. 对于r ∈{n,1,··· ,2n-1}, 有cos(θSC(r)) =-cos(θSC(r-n)).

文献[19] 中所述,‖C‖2和cos(θSC(r)) 可以看作相互独立.

通过上述假设, 当C中的系数与S中的系数选取方式相同时, 可以得知‖C‖2和cos(θSC(r)) 的分布.在给定‖S‖2的分布和Pt的情况下, 可以计算出αPt和βPt, 进而计算出ωPt和QPt.

在文献[19] 中, D’Anvers 等人在选取Pt的数值的时候, 会选取使得ωPt的值取到最小值的Pt. 在本文的实验中, 会延续这一设定.

4.3.2 本文中的方法所带来的提升

在单目标攻击的时候,‖S‖2是一个固定的数值, 所以实际中的βPt的数值会和预期的有所不同, 进而导致实际中的ωPt和QPt与预期有所不同. 对于一个给定的‖S‖2, 将公式(19) 的‖S‖2的分布替换为固定的数值, 可以获得实际中的βPt、ωPt和QPt.

在本节中, 我们将4.2 节中所获得的‖S‖2的分布与D’Anvers 等人所用的卡方分布进行对比, 进而验证本文中的方法的提升. 在选择Pt的时候, 将会选取使得预期ωPt的值取到最小值的Pt.

对于D’Anvers 等人所使用的卡方分布, 我们将4.2 节中所获得的所有的‖S‖2带入, 进而获得实际中的计算开销与解密查询次数, 将其期望值记为ω1和Q1. 然后, 对于4.2 节中所获得的‖S‖2的分布, 将相应的‖S‖2的数值带入, 进而获得实际中的计算开销与解密查询次数, 将其期望值记为ω2和Q2.

经过实验, 得到ω2/ω1≈98.4%,Q2/Q1≈97.0%. 即, 在我们的假设与实验设定下, 实验表明本文中提出的方法可以使“directional failure boosting” 的计算开销与解密查询次数分别降低至98.4% 和97%.

另外, 实验中还将本文中所获得的‖S‖2的分布与相应的正态分布、而不是卡方分布进行对比. 所得到的结果与和卡方分布对比基本一致.

5 总结

本文中提出了一种新的在基于LWE 问题的加密方案中获得解密失败密文的方法. 本文中的方法是“directional failure boosting” 的一个提升, 与“directional failure boosting” 相比, 本文中的方法在效率上有优势, 可以使获得一个解密失败密文所需要的计算开销与解密查询次数分别降低至98.4% 和97%.本文方法还存在两个不足之处, 将在今后的研究工作中继续研究改进.

(1) 在文献[19] 中, D’Anvers 等人提到大多数基于LWE 问题的加密方案都会对密文进行压缩, 进而减少带宽. 但是不论是“directional failure boosting” 还是本文中的方法, 都没有考虑压缩密文所带来的影响.

(2) “directional failure boosting” 的使用前提是至少已经获得一个解密失败密文. 本文假设在使用“directional failure boosting” 之前, 需要用“failure boosting” 来获得至少一个解密失败密文.但是在实际应用中, 即使第一个解密失败密文并不是通过“failure boosting” 获得, “directional failure boosting” 也可以使用. 但是本文中的方法并不适应这种情况.