适用于压缩机定速控制的电-气综合能流计算方法

赵 霞，王 骆，谭 红，戴 蓉

（输配电装备及系统安全与新技术国家重点实验室（重庆大学），重庆市 400044）

0 引言

近年来，为应对能源环境危机、实现低碳可持续发展，综合能源系统（integrated energy system，IES）成为能源领域的新趋势［1-2］。电-气综合能源系统（integrated electricity-gas energy system，IEGS）由电网和天然气网经燃气机组、电转气（power to gas，P2G）装置和电驱动压缩机等耦合形成，是IES 的一种典型形式，电-气协同规划与运行也成为IES 研究的热点问题。

能流计算是IEGS 稳态分析的基本工具以及联合系统规划运行研究的基础，是电网潮流计算和气网水力计算［3］向IEGS 的拓展和延伸。文献［4］提出了气网节点的分类并定性讨论了气网节点法和回路法的优缺点。文献［5］总结了气网节点方程、回路方程和回路-节点方程及其牛顿迭代步骤，是早期的IEGS 能流研究。其后，国内外进一步提出考虑温度［6］、电-气双向耦合［7］及气质影响［8］的IEGS 能流计算模型和方法，利用遗传算法确定气压初值［9］或基于牛顿下山法修正迭代步长［10］以减少节点法对初值的依赖，还开展了考虑不确定性的概率能流研究［11-13］以 及 电-气-热［14-19］、电-气-冷-热［20］和 电-气-水［21］等多能流研究。

根据求解策略，IEGS 能流计算可以分为联立法［6-7，10-13，14-17，19-20］和 分 立 法［8-9，18，21］两 大 类。联 立 法 统一求解电网潮流方程、气网水力学方程和耦合元件方程；分立法根据运行方式分别求解潮流方程和水力学方程，并在耦合环节对两者的结果进行交互。此外，在潮流计算中节点法占据绝对优势，但在气网水力计算中，回路法等其他方法也有广泛应用。目前，IEGS 能 流 计 算 以 节 点 法［6，8-11，13，15-17，19］（即 以 节 点气压为待求变量建立节点方程）为主流方法，仅少量研究考虑回路方程，如文献［14，18，20］以管道流量为待求变量，联解节点方程和回路方程，而文献［7，12，21］以管道流量和节点气压为待求变量，联解节点方程和管道方程。

然而，上述研究对压缩机模型及其适用于能流计算方法的讨论并不充分。一方面，现有研究通常根据压缩机控制模式，将其建模为定出口/入口气压、定压缩比、定气压差或定流量的支路元件［4，15］。对于气网中广泛采用的离心式压缩机，最方便、经济的控制模式为定速控制［3，22］，而前述研究未考虑定速控制模式，工程适用性有局限。另一方面，对于压缩机的各种控制模式，节点法和回路法并不一定直接适用（例如对含压缩机的回路，回路法仅适用于定气压差控制模式），而现有研究对此缺乏系统的讨论。现有IEGS 能流计算方法及其适用的压缩机控制模式详见附录A。

本文研究适用于压缩机定速控制的电-气综合能流计算方法。首先，根据离心式压缩机工作特性，建立定速控制压缩机的支路特性及耗量特性方程；然后，基于节点法和回路法提出适用于定速控制压缩机的扩展节点法、解节点-支路法和扩展节点-回路法，并讨论所提各方法的计算性能及其对压缩机其他控制模式的适应性；最后，采用3 个气网算例和2 个IEGS 算例验证所提方法的有效性及其对压缩机各种控制模式的适用性。

1 IEGS 的稳态模型

IEGS 包含电网、天然气网和电-气耦合元件。电网采用经典交流潮流方程，以下重点说明气网和耦合元件的模型。

1.1 天然气网的稳态模型

气网稳态模型由元件特性方程和拓扑特性方程构成。其中，气源、储气罐和负荷通常建模为定压/定流节点，管道及压缩机特性详述如下。

1.1.1 管道方程

假设气流为一维等温稳定流［3］，高压气网管道方程［23］为：

1.1.2 压缩机及其控制模式

压缩机是实现气体增压输送的重要元件，根据压缩原理可分为活塞式和离心式两大类。活塞式压缩机多用于制备压缩天然气，离心式压缩机因体积小、流量大、供气均匀、运转平稳、经济性好等优势，广泛应用于长输气管道［3，22］。

压缩机按驱动方式可分为电驱动和燃气驱动，接入节点i、j的压缩机的示意图如附录B 图B1 所示。压缩机原动机所需功率［24］为：

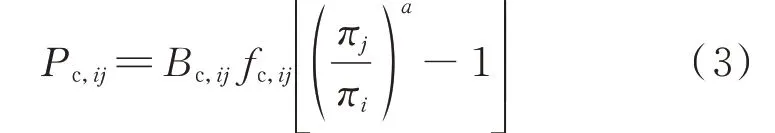
式 中：fc，ij和Pc，ij分 别 为 压 缩 机ij的 流 量 和 所 消 耗 功率；Bc，ij为压缩机常数；a=(k-1)/k，其中k为比热容比。

电驱动压缩机实质是一种电-气耦合元件，需要将Pc，ij作为等效电负荷。对于燃气驱动压缩机，通常将Pc，ij转化为首节点气负荷［25］：

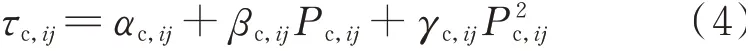
式中：τc，ij为燃气轮机消耗的气流量；αc，ij、βc，ij、γc，ij为耗量系数。

式（3）、式（4）仅给出压缩机耗量特性，在能流计算中还需根据压缩机控制模式补充支路方程才能满足定解条件。现有研究仅考虑定出口/入口气压、定压缩比、定气压差及定流量控制［4，15］，本文进一步考虑离心式压缩机广泛采用的定速控制模式。

离心式压缩机的工作特性可用图1 所示的一组曲线描述，每条曲线对应某转速下压缩机绝热压头与入口流量的稳态关系［26］。

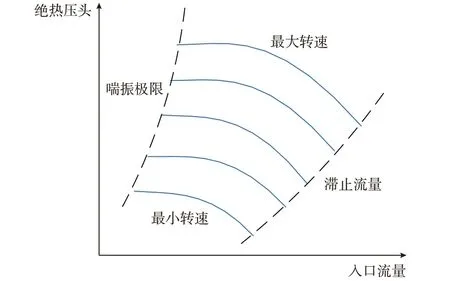
图1 离心式压缩机工作特性示意图Fig.1 Schematic diagram of operation characteristics for centrifugal compressor

式中：Z和R分别为压缩因子及气体常数；Ts为入口气体温度。

联立式（5）和式（6），有

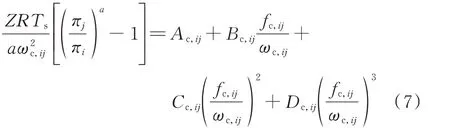
式（7）即定速控制压缩机的支路特性方程。与其他控制模式不同，定速控制压缩机的转速给定，其支路特性由出口/入口气压和流量共同刻画。式（7）可表示为如下的一般形式：

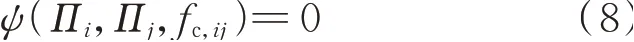
需注意的是，式（2）表明管道流量为节点气压的显函数，而压缩机流量则为节点气压的隐函数。此外，结合式（3）、式（4）及式（7）可知，若定速控制压缩机由燃气驱动，其耗量仅为流量的函数τ(fc，ij)，即有：

1.1.3 节点方程及回路方程

与电网类似，气网同样满足基尔霍夫第一定律（KCL）和基尔霍夫第二定律（KVL）。

根据KCL，流入任一节点流量的代数和为零，即满足节点流量连续性方程（简称“节点方程”）：

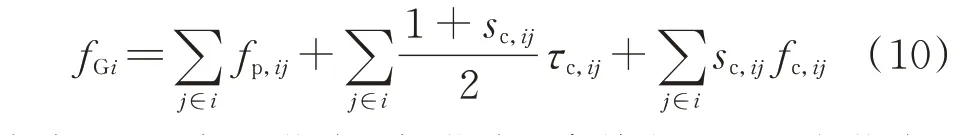
式中：j∈i表示节点j与节点i直接相连；fGi为节点i的注入气流量；sc，ij为压缩机气流方向指示变量，当节点i为入口节点时sc，ij=1，为出口节点时sc，ij=-1。

根据KVL，任一闭合回路中各支路两端气压（平方）差的代数和为零，即满足如下回路方程：

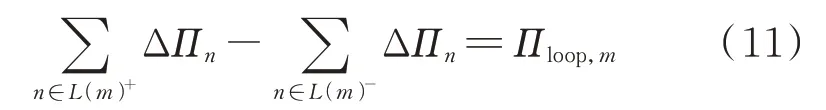
式中：L（m）+和L（m）-分别为回路m中与回路方向相同、相反的支路集合；ΔΠn为支路n两端气压平方差；Πloop，m为回路能量差。若m为闭合回路（简称“实回路”），则Πloop，m=0；若m为虚回路（即连接任意2 个定压节 点的路径），则Πloop，m为沿虚回路方向2 个定压节点的气压平方差。

1.2 电-气耦合元件

本文考虑燃气机组、P2G 装置及电驱动压缩机。电驱动压缩机消耗的电功率由式（3）确定。

燃气机组利用天然气生产电能［11］：

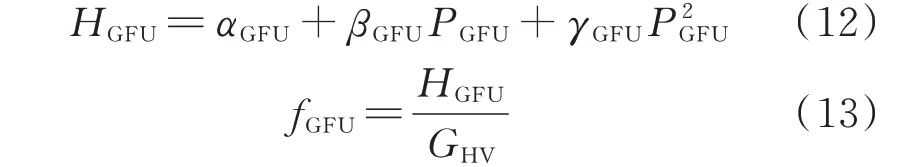
式中：HGFU和fGFU分别为燃气机组的热功率和耗气量；PGFU为燃气机组输出电功率；GHV为天然气热值；αGFU、βGFU、γGFU为燃气机组耗热系数。

P2G 的电-气耦合关系为［27］：

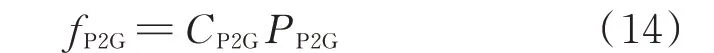
式中：fP2G和PP2G分别为P2G 产生的气流量及消耗的电功率；CP2G为能量转化系数。

2 适用于定速控制的3 种气网水力计算方法

本章考虑压缩机定速控制模式，提出3 种气网水力计算方法，所提方法对其他控制模式的适应性分析见附录C。此外，水力计算中的电驱动压缩机可视为耗量为0 的燃气驱动压缩机，下文仅以燃气驱动压缩机为例说明所提方法。

假设气网节点数为ng（其中定压节点数为n0，其余为定流节点），管道数为p，压缩机台数为c，实际回路数为l，由图论有以下关系［3］：

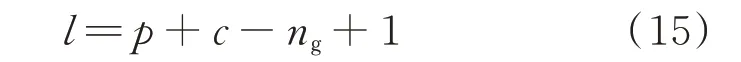
当气网有多个定压节点，选其中一个节点（即主节点）与其余定压节点形成虚回路，则虚回路数量为n0-1。

气网待求变量与水力学方程如表1 所示。

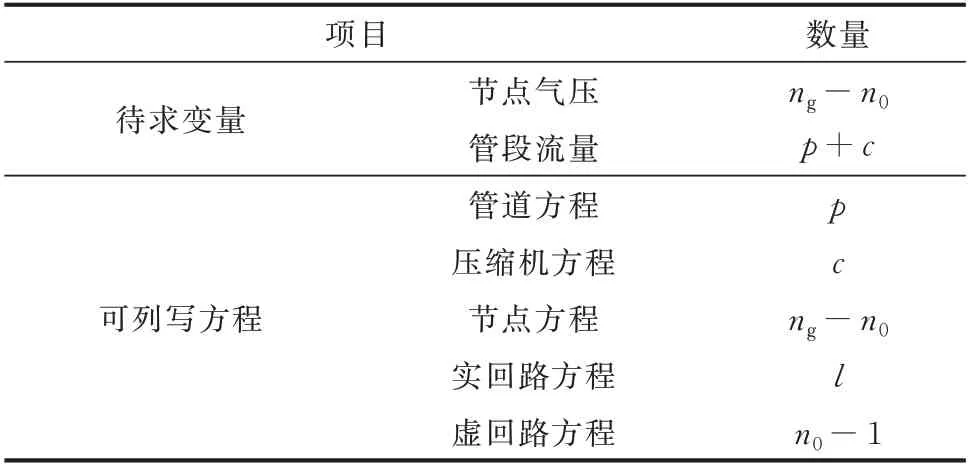
表1 天然气网的待求变量与水力学方程Table 1 Unsolved variables and hydraulic equations of natural gas network

2.1 方法1：扩展节点法

节点法以节点气压为待求变量，求解节点方程。然而，定速控制压缩机的流量为气压的隐函数，节点法无法直接适用。为此，本文引入定速控制压缩机的支路方程（式（8））并新增压缩机流量fc，ij为待求变量，即扩展节点法。

扩展节点法的水力学方程为：

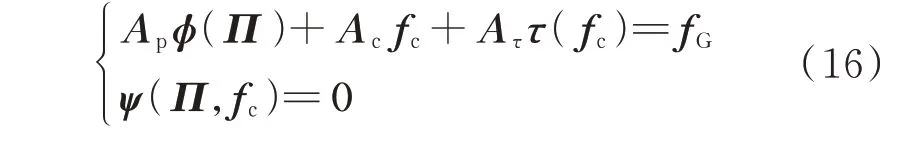
式中：Ap、Ac和Aτ分别为定流节点与管道、压缩机及燃气驱动压缩机的关联矩阵；Π和fc分别为节点气压与压缩机流量列向量；fG为定流节点注入气流量列 向 量；ϕ(·)、ψ(·)和τ(·)分 别 表 示 管 道 方 程（式（2））、压 缩 机 支 路 方 程（式（8））和 其 耗 量 方程（式（9））。

Aτ表征燃气驱动压缩机耗气量等效负荷的接入节点关联矩阵，其元素aij=1 表示压缩机j的耗气负荷接入节点i，否则aij=0。Ap和Ac的定义类似，以Ap为例，其元素为：

式（16）是非线性方程组，采用Newton-Raphson（N-R）法求解。由式（16）解得节点气压及压缩机流量后，由管道方程可求解出各管道流量。

2.2 方法2：解节点-支路法

在扩展节点法的基础上，将管道流量同时作为待求变量并补充管道方程，即形成方法2。该方法同时求解各节点气压和各支路流量，称为“解节点-支路法”。

解节点-支路法的水力学方程为：

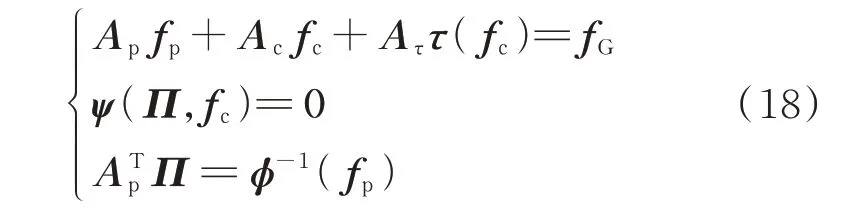
式中：ϕ-1(·)为管道方程（式（2））的反函数，表征管道气压平方差与流量的函数关系；fp为管道流量列向量。

式（18）同样是非线性方程组，规模较式（16）增加p个，但由于扩展了支路流量作为待求变量，应用N-R 法求解时，方法2 的初值依赖性和工况适应性较方法1 有明显改善（详见算例分析）。

2.3 方法3：扩展节点-回路法

以上2 种方法的待求变量包含所有节点气压，应用N-R 法求解时难以设置气压初值。为此，本文进一步基于气网的解管段流量法［3］研究以各支路流量为主要待求变量的计算方法。

解管段流量法以管段流量为待求变量，联解节点方程和回路方程（简称“节点-回路法”），与节点法相比，具有初值依赖性小的突出优势［4-5］，但对于含压缩机回路，该方法仅适用于定压差控制模式。为此，本文基于解管段流量法，提出以各支路流量为主要待求变量、适用于多种压缩机控制模式的扩展节点-回路法。

扩展节点-回路法的水力学方程随气网拓扑结构及定速控制压缩机所处位置不同而不同。为此，将气网分为如表2 所示的3 种类型。本节重点说明如何应用方法3 构建不同类型气网的水力学方程，具体计算流程见附录D。

表2 天然气网分类Table 2 Classification of natural gas network

2.3.1 树状网

树状网不含回路，方法3 退化为以支路流量为待求变量的节点方程法，其水力学方程为：

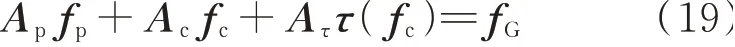
由于τ(·)的非线性，式（19）仍是一组非线性方程。若压缩机均为电驱动，则式（19）为线性方程。由式（19）解得各支路流量后，再由管道及压缩机支路方程（式（2）、式（8））求解各节点气压。

2.3.2 Ⅰ型环网

仍以支路流量为待求变量，Ⅰ型环网的方程为：

2.3.3 Ⅱ型环网

Ⅱ型环网的回路方程中含压缩机，需要引入压缩机气压变量。同时，由于压缩机气压变量的引入，需要在节点方程和回路方程的基础上，进一步补充主节点和压缩机入口节点之间的等效虚回路方程。因此，Ⅱ型环网的水力学方程为：

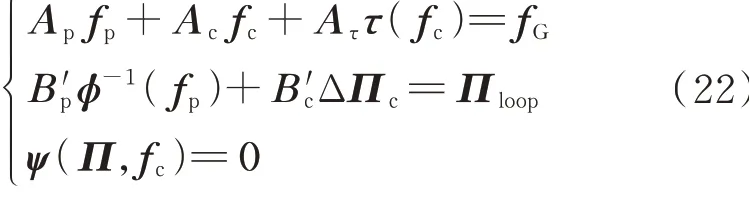
式中：Bp′ 和B′c分别为管道-回路关联矩阵及压缩机-回路关联矩阵，其元素定义与Bp类似，区别在于B′p和B′c对应的回路包含实回路、虚回路和等效虚回路；ΔΠc为压缩机支路气压差列向量。

为简化N-R 法求解式（22）时雅可比矩阵的计算，可以用压缩机入口气压和压缩比作为变量来建立Ⅱ型环网的水力学方程。

2.4 3 种方法的比较

表3 从建模依据、方程规模及初值依赖性等方面对3 种方法进行定性比较。由于气网管道一般多于节点，而压缩机数量较少，方法1 的方程规模一般小于方法3。由表3 可见，方法3 是含定速控制压缩机气网水力计算的首选方法，其缺点是需要进行拓扑分析以获取回路信息，方程建立较困难。方法1和2 无须拓扑分析，方法2 计算规模大，但性能优于方法1。下文将通过算例定量比较3 种方法。

表3 所提3 种方法的比较Table 3 Comparison of proposed three methods

3 IEGS 的稳态能流计算

IEGS 能流计算本质上是联立或分立求解电网潮流方程、气网水力学方程和电-气耦合元件方程。由于本文方法的区别在于气网水力学方程，结合潮流方程和电-气耦合元件方程，所提方法可以直接推广应用于IEGS 能流计算。限于篇幅，仅通过IEGS算例分析本文方法的能流计算性能。

4 算例分析

用多个算例验证本文3 种方法的有效性，并对比分析其对N-R 法初值的依赖性和工况适应性。算例接线见附录E，详细数据见文献［28］。所有仿真均在MATLAB R2016a 平台进行，计算环境为1.20 GHz Intel Core i5-1035G7 CPU、8 GB RAM 笔记本电脑。

4.1 天然气网的水力计算

选取树状网、Ⅰ型环网和Ⅱ型环网3 个气网算例进行水力计算。N-R 法初值选取原则为：1）以定压节点为参考，沿输气方向，按管道首、末端气压相差5%～10%设置气压初值（记为Π0）［6，16］；2）考虑如图1 所示的压缩机运行边界，计算设计流量上下限的中点值，再取全部压缩机中点值的均值作为支路流量初值（记为f0）；3）压缩比初值设为1。

本节3 个算例均考虑2 种场景。

场景1：考察初值依赖性。以Π0和f0为参考，按k1Π0和k2f0选取气压和流量初值，其中k1和k2分别为 气 压、流 量 初 值 系 数，取k1∈[0.7，1.3]，k2∈[0，2]。在k1和k2的 取 值 范 围 内 等 间 距 各 选 取100 个样本，从而形成10 000 个初值样本，再应用3 种方法对所得样本进行水力计算。

场景2：考察工况适应性。由于3 种方法均涉及求解部分或全部支路流量，仍沿用场景1 的方法选取支路流量初值并按Π0设置气压初值。此外，以原始负荷（记为fL0）为参考，假设负荷水平按k3fL0变化，其中k3为负荷水平系数，取k3∈[0.7，1.3]。与场景1 类似，等间距选取k2和k3形成10 000 个样本，再应用3 种方法进行水力计算。

4.1.1 算例1（20 节点树状网）

场景1 下3 种方法的收敛性及计算时间如表4所示，表中迭代次数及计算时间均为收敛样本的平均值。图2 用节点气压和支路流量初值范围来刻画3 种方法的收敛域，图中蓝色散点表示收敛样本。

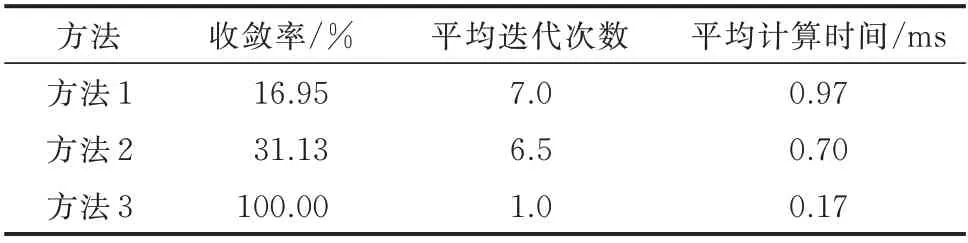
表4 算例1 中3 种方法的收敛性和计算时间（场景1）Table 4 Convergence and computation time of three methods in case 1 (scenario 1)

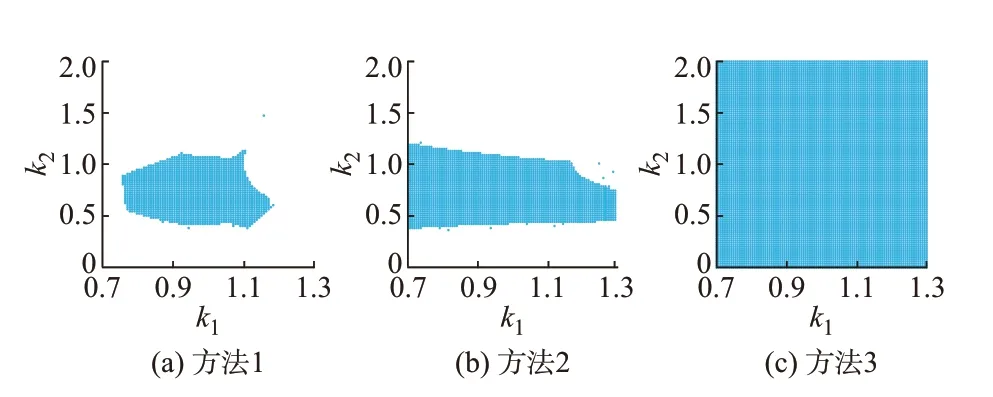
图2 算例1 中3 种方法的收敛域（场景1）Fig.2 Convergence domain of three methods in case 1(scenario 1)

由表4 可见，方法1、2 的迭代次数相当，但方法2的收敛性有显著改善。方法3 全部收敛且迭代次数明显优于前2 种方法。此外，方法1、2 的计算时间相当，而方法3 用时最少，这是因为算例1 为树状网，拓扑分析用时极少。由图2 可见，方法1 收敛域对应的气压及流量初值范围较小，方法2 的气压初值收敛范围则明显放宽。

场景2 下3 种方法的收敛性及计算时间如表5所示。由表5 可见，方法3 仍保持最高的收敛率和求解效率，工况适应性良好，而方法2 次之，方法1 最差。其中，由于算例1 为树状网，应用方法3 时所有样本均能解得一组收敛解，但对于负荷水平较高的样本，部分气压为负，本文将其视为不收敛样本。

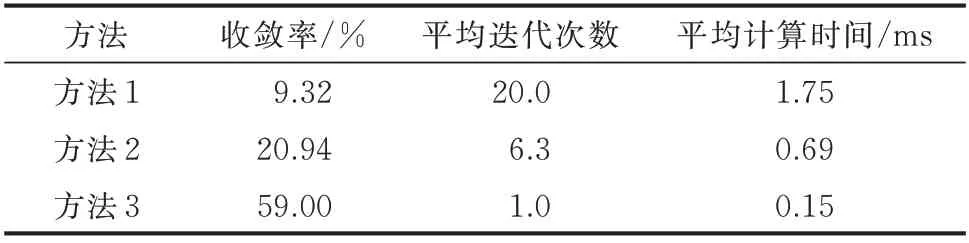
表5 算例1 中3 种方法的收敛性和计算时间（场景2）Table 5 Convergence and computation time of three methods in case 1（scenario 2）

综合场景1、2 可见，对于树状网，方法3 的收敛性和用时均明显优于前2 种方法，方法1 的性能最差，而与方法1 相比，方法2 的性能有明显提升。以上结果表明，方法3 的初值依赖性小、工况适应性好，是气网水力计算的首选方法。

4.1.2 算例2（11 节点Ⅰ型环网）

场景1 下3 种方法的收敛性、计算时间及收敛域分别如表6 和图3 所示。

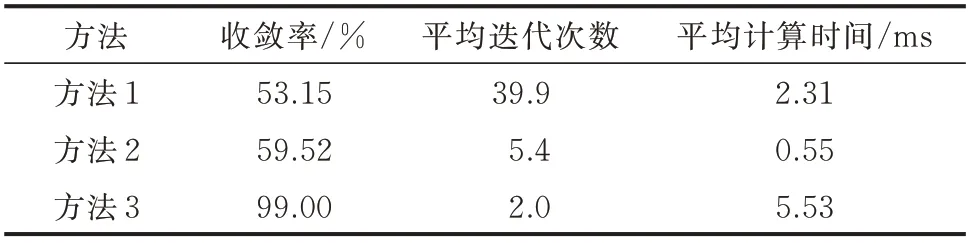
表6 算例2 中3 种方法的收敛性和计算时间（场景1）Table 6 Convergence and computation time of three methods in case 2 (scenario 1)

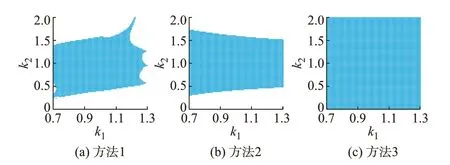
图3 算例2 中3 种方法的收敛域（场景1）Fig.3 Convergence domain of three methods in case 2(scenario 1)

由表6 可见，方法1 的收敛率最低且迭代次数远大于方法2、3。方法2 的收敛率较方法1 仅有小幅提升，但迭代次数明显降低。方法3 在收敛率为99%的情况下可靠收敛，迭代次数较方法1、2 有明显优势。计算时间方面，方法2 最少，方法1 次之，由于方法3 需进行拓扑分析，用时明显增加（计算总时间为5.53 ms，拓扑分析时间为5.32 ms，占比超过90%），但所需时间仍然很少，表明拓扑分析对方法3 计算效率的影响不大。此外，由图3 可见，方法1、2 的流量初值k2取过大或过小都不利于收敛，而方法3 仅在k2为0 时不收敛。

场景2 下3 种方法的收敛性及计算时间如表7所示。其中，方法3 的不收敛样本同样仅含k2为0 的样本。可见，方法3 在收敛性及迭代次数方面仍然具有明显优势，表明方法3 对工况变化的适应性良好，而方法2 次之，方法1 最差。

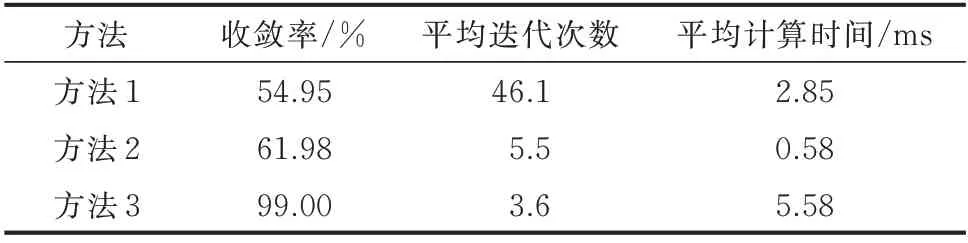
表7 算例2 中3 种方法的收敛性和计算时间（场景2）Table 7 Convergence and computation time of three methods in case 2 (scenario 2)

综合场景1、2 可见，对于Ⅰ型环网，方法1 的整体性能最差，方法2 的收敛性较方法1 有小幅提升，但迭代次数和用时显著降低。方法3 的初值依赖性和工况适应性明显优于方法1、2（但应避免流量初值取0），尽管由于拓扑分析，其用时明显增加，但2 种场景的计算时间均小于6 ms，总体计算性能良好。

4.1.3 算例3（48 节点Ⅱ型环网）

场景1 下3 种方法的收敛性、计算时间及收敛域分别如表8 和图4 所示。由表8 可见，方法1 的收敛率最低且迭代次数显著多于另2 种方法。与方法1相比，方法2 的收敛率有小幅改善，但迭代次数显著降低。方法3 与方法2 迭代次数相当，但收敛性进一步提升。计算时间方面，方法2 用时最少，方法1次之，方法3 用时最多（计算总时间为16.33 ms，拓扑分析时间约为13.52 ms，占比约为80%）。由图4进一步可见，3 种方法收敛域对应的气压初值范围相当。对于流量初值范围，方法3 最宽，方法2 次之，方法1 最窄，且随着气压初值增大，方法1、2 收敛域对应的流量初值范围明显收窄。

表8 算例3 中3 种方法的收敛性和计算时间（场景1）Table 8 Convergence and computation time of three methods in case 3 (scenario 1)

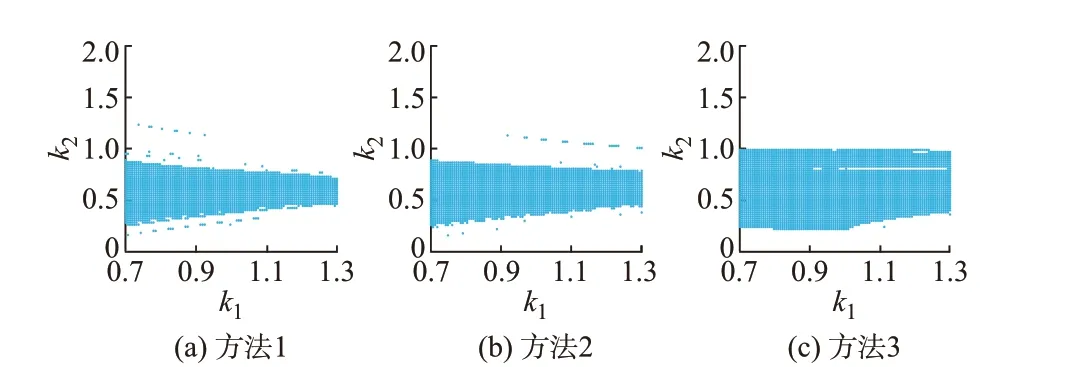
图4 算例3 中3 种方法的收敛域（场景1）Fig.4 Convergence domain of three methods in case 3(scenario 1)

场景2 下3 种方法的收敛性及计算时间如表9所示。从表中可以看出，方法2、3 的收敛性显著优于方法1。与方法2 相比，方法3 的收敛性有一定提升，但迭代次数有小幅增加。

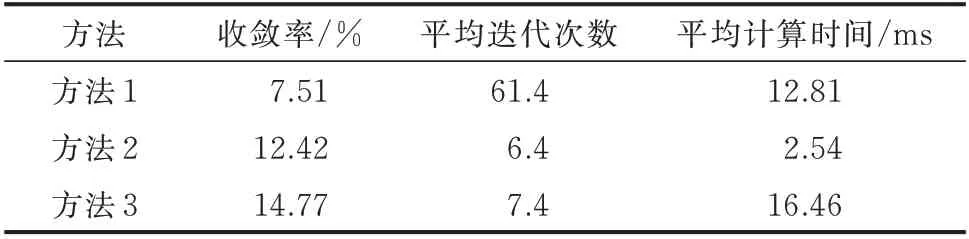
表9 算例3 中3 种方法的收敛性和计算时间（场景2）Table 9 Convergence and computation time of three methods in case 3 (scenario 2)

综合场景1、2 可见，对于Ⅱ型环网，方法3 的收敛性最好，方法2 次之，方法1 最差。方法3 用时大于方法1、2，但2 种场景下都在0.02 s 内完成计算，总体性能良好。进一步对比算例2、3 可见，随着系统规模增加，3 种方法的用时均显著增大，但均小于0.02 s。此外，方法3 拓扑分析时间占比下降，表明随着系统规模的增加，拓扑分析对方法3 计算效率的影响进一步降低。

为方便对不同类型算例进行纵向比较，将上述3 个算例中各场景下的收敛率汇总于图5。

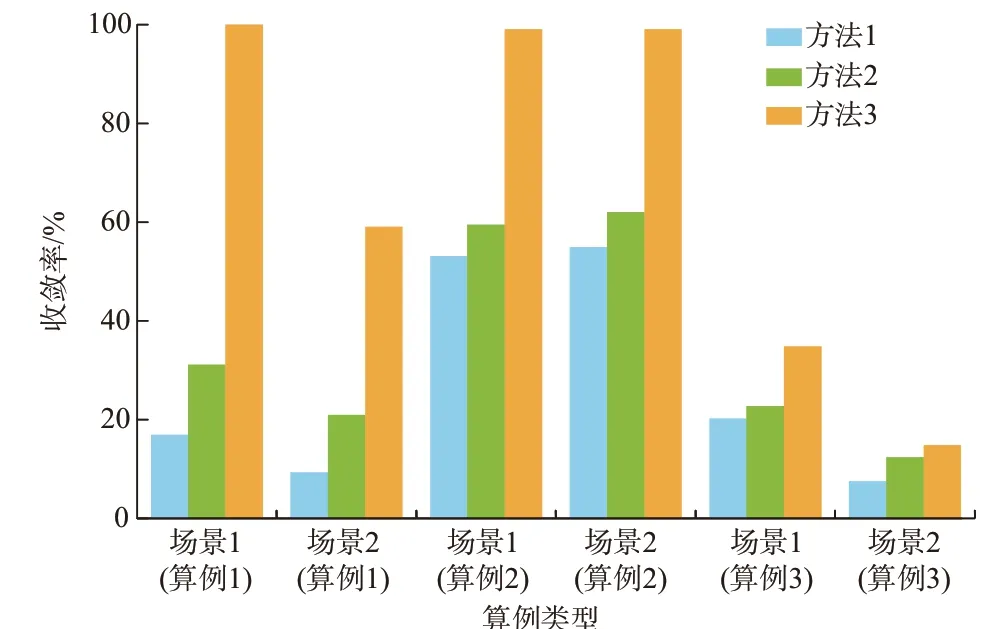
图5 3 个算例的收敛率Fig.5 Convergence rate of three cases

由图5 可见，对于各类型算例，方法3 初值依赖性和工况适应性均为最佳，方法2 次之，方法1 最差。特别是对于树状网和Ⅰ型环网，方法3 较方法1、2 有绝对优势，而在Ⅱ型环网中，该优势程度有所削弱。此外，与算例1、3 相比，算例2 中方法1、2 的收敛性均有明显提升，表明这2 种方法更适用于Ⅰ型环网。

附录F 用算例3 对比分析了压缩机控制模式对水力计算的影响，并进一步验证本文3 种方法对压缩机其他控制模式的适用性。

4.2 电-气综合能流计算

用IEEE 39 节点电网+20 节点气网（算例4）和IEEE 118 节点电网+48 节点气网（算例5）验证本文方法对IEGS 能流计算的有效性，重点分析联立求解和分立求解2 种策略下3 种方法对初值的依赖性。

假设燃气机组耗气量恒定且P2G 装置产气量恒定。电网采用平启动，气网按4.1 节场景1 的初值设置方式选取10 000 个样本，分别应用本文3 种水力计算方法联立、分立求解IEGS 能流，结果如表10和表11 所示。

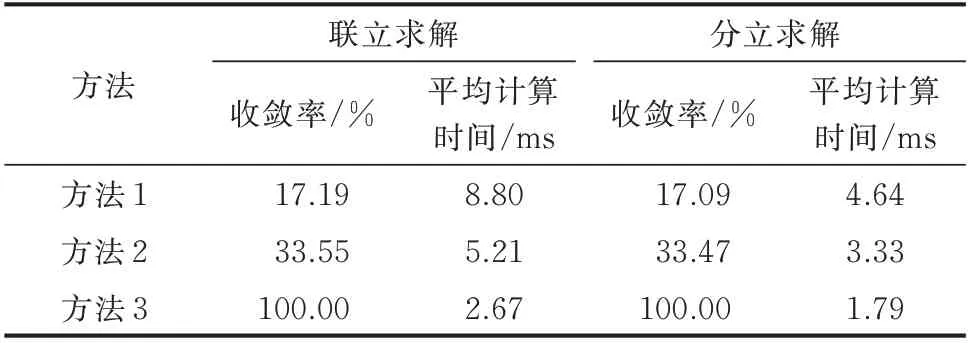
表10 算例4 中3 种方法的收敛性和计算时间Table 10 Convergence and computation time of three methods in case 4

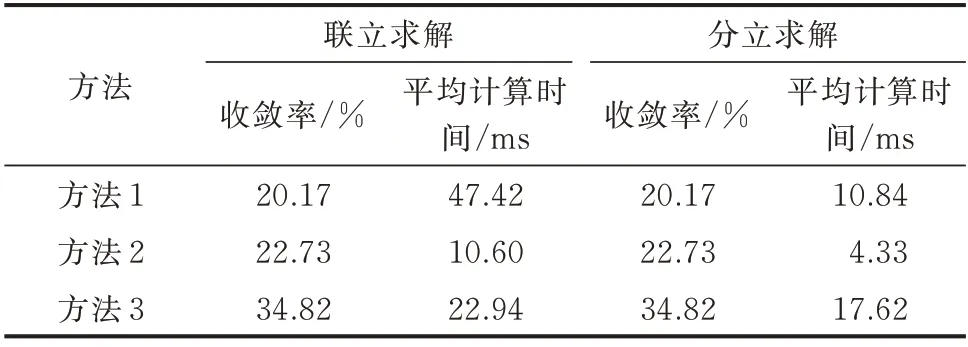
表11 算例5 中3 种方法的收敛性和计算时间Table 11 Convergence and computation time of three methods in case 5

由表10 和表11 可见，3 种方法的收敛性均不受求解策略影响。对比气网相同的算例结果（即表4和表10、表8 和表11）可见，3 种方法的收敛率基本一致，表明IEGS 能流计算对初值的依赖性主要取决于气网。进一步对比3 种方法的收敛性可见，对于算例4（树状气网），方法3 的收敛性有显著优势，而方法1、2 对初值的依赖性较大，方法1 尤其突出（其收敛率约为方法2 的1/2、方法3 的1/6）；对于算例5（Ⅱ型环网），方法3 的收敛性仍然优于前2 种方法（其收敛率较方法1 提高70%、较方法2 提高50%）。从计算时间来看，方法3 应用于算例4 时耗时最少，而应用于算例5 时，由于拓扑分析导致其不再具有时间优势，但2 种策略下方法3 仍能在20 ms左右完成能流计算。

综合以上全部算例可见，与方法1、2 相比，方法3的收敛性均有明显优势，而计算时间可接受，表明对气网水力计算及IEGS 能流计算而言，方法3 都是总体计算性能最佳的方法。

5 结语

考虑气网广泛采用的离心式压缩机及其定速控制模式，提出了适用于压缩机定速控制的扩展节点法、解节点-支路法和扩展节点-回路法，并将其推广应用于IEGS 能流计算。对比分析了3 种方法的可解性、计算规模和收敛性，并讨论了所提方法对定压缩比、定气压差等控制模式的适应性。

不同结构及规模的气网和IEGS 算例分析表明：扩展节点-回路法的初值依赖性小，工况适应性好，但需要进行拓扑分析；节点法无须拓扑分析，计算规模小，但初值依赖性强、工况适应性差；解节点-支路法是前两者的折中，无须进行拓扑分析，且初值依赖性和工况适应性良好。

后续将研究适用于压缩机定速控制的电-气动态能流计算方法。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。