考虑荷电状态恢复的储能一次调频控制策略
严干贵,王铭岐,段双明,张 薇,李军徽,蔡长兴
(1. 现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林省吉林市 132012;2. 国网江西省电力公司赣州供电公司,江西省赣州市 341000)
0 引言
随着能源系统清洁化转型战略的深入推进,中国清洁能源占比逐步提高,其中,以风能、太阳能为代表的清洁能源正逐步取代传统化石能源,电力系统逐渐呈现出“高比例可再生能源渗透”的特点[1-3]。然而,清洁能源发电的随机性和波动性将导致电源侧功率波动加剧,给电网调频带来巨大的挑战。因此,亟须引入一种新的调频手段来缓解传统调频机组的调频压力[4-5]。电池储能系统(battery energy storage system,BESS)作为解决清洁能源并网的有效手段,凭借其精确跟踪、响应速度快、控制精度高、具有双向调节能力等优点在一次调频领域备受关注[6-9]。
国内外学者已经从储能调频模型和储能控制策略等方面开展了关于电池储能系统参与电网一次调频的研究。文献[10]推导出适用于电网一次调频的储能简化模型,并验证了储能调频模型的有效性。文献[11]采用固定的虚拟下垂系数对储能出力进行控制(即定K下垂控制),并提出了储能容量的配置方法。文献[12]考虑储能调频出力的自适应性,将虚拟下垂系数定义为储能荷电状态(state of charge,SOC)的函数(即变K下垂控制),有效避免了储能可能出现的过充、过放现象。文献[13]在火电机组的调频死区内设置恰当的储能调频死区,有效减少了常规机组的动作次数,提高了储能和常规机组运行的经济性。文献[14]提出利用权重因子调节虚拟惯性控制和虚拟下垂控制出力比重的储能调频策略,有效减小了电网频率波动。文献[15]提出一种分配系数模型实现虚拟惯性控制和虚拟下垂控制的平滑切换,有效避免了2 种控制策略直接切换对电网的二次冲击。文献[16]考虑储能的电量管理,充分利用调频死区并基于SOC 基点提出一种储能SOC 恢复策略,以保证储能SOC 长时间处于良好状态。
上述研究在电池储能系统参与电网一次调频的控制策略方面存在以下不足:当前研究主要集中在虚拟惯性控制和虚拟下垂控制的协调配合和切换时机 方 面[13-15,17-18],实 现 了2 种 控 制 策 略 的 优 势 互 补,有效改善了调频效果,但却没有从调节系数方面考虑当储能SOC 偏低或偏高时储能调频功率不足导致调频效果不理想的问题。文献[14]在储能SOC恢复阶段提出储能SOC 恢复方法,一定程度上解决了此问题,但却没有在储能调频阶段提出合理的控制策略来解决此问题,同时所提储能SOC 恢复方法仍有待改善。
为了解决储能SOC 偏低或偏高时储能调频能力不足的问题,从而更好地满足系统调频需求,本文提出一种考虑SOC 恢复的储能一次调频控制策略。在储能调频阶段,储能SOC 偏低时增加储能充电功率(储能SOC 偏高时增加储能放电功率),使储能SOC 向理想状态恢复,为储能后续调频提供放电(充电)空间;在储能SOC 恢复阶段,合理选取储能SOC 恢复系数,调整SOC 恢复速率使其具备较强的双向调频能力。最后,搭建储能参与电网一次调频仿真系统,对所提调频策略的有效性进行了仿真验证。
1 含储能的电网一次调频模型
基于区域等效的原理,建立含储能的电网一次调频模型[14],其框图如图1 所示。图中:s为拉普拉斯算子;KG为火电机组单位调节功率;Tg为火电机组调速器时间常数;FHP为汽轮机再热器增益;TRH为再热器时间常数;TCH为汽轮机时间常数;Gg(s)为火电机组传递函数;ΔPG(s)为火电机组出力;e0(s)为系统一次调频分配给储能的信号;TE为储能响应时间常数;GE(s)为储能电池的传递函数;Pb为系统一次调频分配给储能的功率,并规定Pb>0 表示储能处于放电状态,Pb<0 表示储能处于充电状态;η为电池储能系统的充放电效率;Erated为电池储能系统的额定容量;Sinitial为电池储能系统的初始SOC;ΔPE(s)为电池储能系统出力;ΔPL(s)为综合负荷扰动;M为电网惯性时间常数;D为系统阻尼系数;ΔF(s)为系统频率偏差。
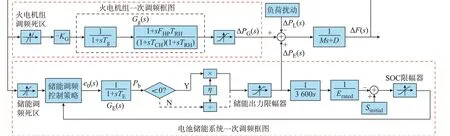
图1 含储能的电网一次调频模型框图Fig.1 Block diagram of primary frequency regulation model for power grid with BESS
2 考虑SOC 恢复的储能一次调频控制策略
2.1 储能一次调频控制策略框架
储能的调频能力和SOC 密切相关[19]。当储能SOC 偏低或偏高时,双向调频能力会受到限制,为了使储能保持较强的双向调频能力,从而更好地满足系统调频需求,储能SOC 应尽可能维持在良好状态。因此,本文以电池储能系统的调频死区上下限±Δfdb为界限,将储能参与电网一次调频划分为储能调频阶段(系统频率偏差在储能调频死区外,即|Δf|>Δfdb)和储能SOC 恢复阶段(系统频率偏差在储能调频死区内,即|Δf|≤Δfdb)。在储能调频阶段,将变K下垂控制(主调频控制)与辅调频控制的充放电系数相加作为储能调频系数,进而控制储能调频阶段的出力,使储能SOC 更快恢复到良好状态以改善储能后续时段的调频能力;在储能SOC 恢复阶段,在保证系统频率偏差不跌出储能调频死区的基础上,对储能SOC 进行恢复。基于上述思路,本文提出一种考虑SOC 恢复的储能一次调频控制策略,其整体框架如图2 所示。
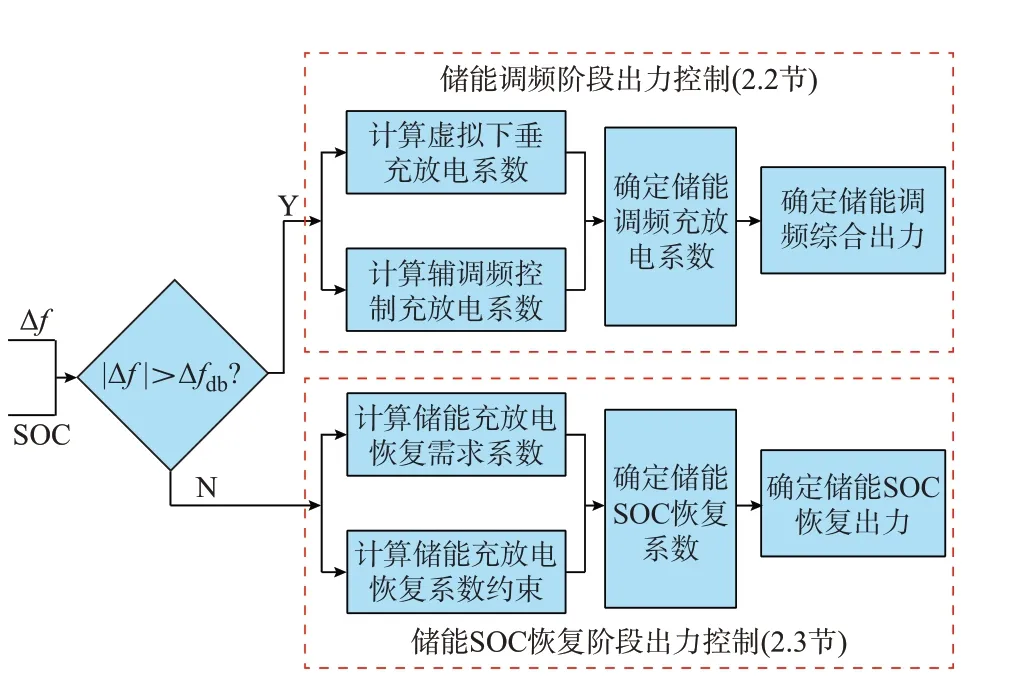
图2 储能一次调频控制策略框架Fig.2 Framework of primary frequency regulation control strategy of BESS
2.2 储能调频阶段出力控制
为避免储能SOC 在长时间扰动中快速消耗殆尽或饱和,本文首先采用变K下垂控制作为主调频控制对电网频率进行调节[12],但变K下垂控制仍然存在一些不足。为解决变K下垂控制在储能SOC偏低或偏高时储能调频能力不足的问题,本文提出2.2.2 节的辅调频控制,此控制在储能调频阶段与2.2.1 节的变K下垂控制结合使用共同对电网频率进行调节。
本文提出的辅调频控制不局限于与变K下垂控制结合使用,变K惯性控制以及变K下垂控制和变K惯性控制协调配合的控制都可以借鉴本文辅调频控制的构建思路,以解决储能SOC 偏低或偏高时储能调频能力不足的问题。本文仅以变K下垂控制作为主调频控制为例,对辅调频控制的构建方法和储能调频系数的计算方法进行说明。
2.2.1 变K下垂控制
储能通过变K下垂控制参与频率调节。变K下垂控制出力ΔPE1与频率偏差Δf的关系为:
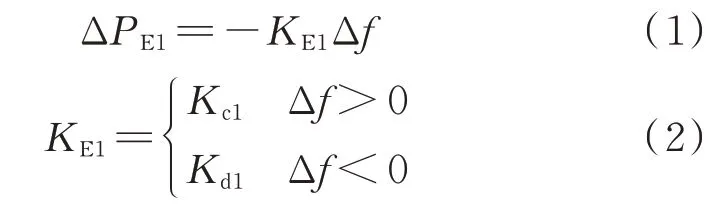
式中:KE1为虚拟下垂系数;Kc1为虚拟下垂充电系数;Kd1为虚拟下垂放电系数。
当储能SOC 偏低时,Kc1设置为最大值,使得储能具有良好的调频效果,而Kd1设置较小且随着储能SOC 的降低而减小;当储能SOC 偏高时,Kd1设置为最大值,使得储能具有良好的调频效果,而Kc1设置较小且随着储能SOC 的升高而减小[12]。基于上述分析,采用S 型函数对虚拟下垂充放电系数进行构建。S 型函数的特点是:初始阶段近似呈指数增长,随着逐渐饱和,增加速度减慢,达到一定程度时停止增加,并稳定在某一数值。以储能SOC 值S为自变量,Kc1和Kd1为因变量,建立虚拟下垂充放电系数表达式如式(3)和式(4)所示。
式 中:KE,max为 虚 拟 下 垂 系 数 的 最 大 值;Smin、Slow、Shigh、Smax分别为储能SOC 的最小值、较低值、较高值、最大值;n为曲线的自适应系数,其值决定了曲线的变化趋势。当n取不同值时,虚拟下垂系数的变化曲线如附录A 图A1 所示。
由附录A 图A1 可知,当n值较大时,KE1仅在很小的一段范围内跟随储能SOC 有较大变化,自适应度较弱;而当n值较小时,一定程度上影响了储能的调频效果。因此,本文n取中间值15,在保证储能调频效果的同时,也兼顾了KE1随储能SOC 变化的自适应性。
2.2.2 辅调频控制
本文设计此控制的目的是在储能SOC 偏低(偏高)时,通过辅调频控制使储能以更大功率进行充电(放电),以便储能SOC 更快地向理想状态恢复,改善储能后续的放电(充电)调频能力。
辅调频控制的动作时机由系统频率偏差和储能SOC 决定。以储能SOC 值S为横坐标,系统频率偏差为纵坐标,构建辅调频控制动作时机图,如附录A图A2 所示。图中的4 条虚线中,与横坐标平行的2 条虚线代表储能调频死区的上下限;与纵坐标平行的2 条虚线代表储能SOC 处于理想状态的边界,即Slow≤S≤Shigh时,储能SOC 为理想状态。储能调频阶段所在区域,即|Δf|>Δfdb的区域,4 条虚线将其分为6 个区域。
区域Ⅰ的Δf>Δfdb且S<Slow,Δf为正,需要储能充电调频以降低系统频率,而此时储能SOC 处于较低状态,若此时进行辅调频控制(储能进行充电),不仅可以使储能SOC 恢复到较好的状态以改善储能后续的放电调频能力,同时也提升了储能当前的充电调频能力;同理,区域Ⅵ的Δf<-Δfdb且S>Shigh,Δf为负,需要储能放电调频以提高系统频率,而此时储能SOC 处于较高状态,若此时进行辅调频控制(储能进行放电),不仅可以使储能SOC 恢复到较好的状态以改善储能后续的充电调频能力,同时也提升了储能当前的放电调频能力。因此,在区域Ⅰ、Ⅵ储能采用变K下垂控制+辅调频控制。
区域Ⅲ的Δf>Δfdb且S>Shigh,Δf为正,需要储能充电调频以降低系统频率,而此时储能SOC 处于较高状态,若此时进行辅调频控制(储能进行放电),会影响系统频率的降低,违背了储能调频阶段调频这一主要目标;同理,区域Ⅳ的Δf<-Δfdb且S<Slow,Δf为负,需要储能放电调频以提高系统频率,而此时储能SOC 处于较低状态,若此时进行辅调频控制(储能进行充电),会影响系统频率的提高,违背了储能调频阶段调频这一主要目标。因此,在区域Ⅲ、Ⅳ储能只采用变K下垂控制。
区域Ⅱ、Ⅴ的储能SOC 处于理想状态,若此时进行辅调频控制,虽然可以提升储能当前的调频能力,但储能SOC 可能会很快跌出理想状态范围,影响储能后续的调频能力。因此,在区域Ⅱ、Ⅴ储能只采用变K下垂控制。
综上,在区域Ⅰ、Ⅵ储能采用变K下垂控制+辅调频控制,在区域Ⅱ、Ⅲ、Ⅳ、Ⅴ储能只采用变K下垂控制。同时,在区域Ⅰ,辅调频控制充电系数应设置较大且随着储能SOC 的升高而减小;在区域Ⅵ,辅调频控制放电系数应设置较大且随着储能SOC 的降低而减小。
结合上述分析,采用S 型函数对辅调频控制充放电系数进行构建。以S为自变量,辅调频控制充放电系数为因变量,建立辅调频控制充放电系数表达式如式(5)和式(6)所示。

式中:Kc2为辅调频控制充电系数;Kd2为辅调频控制放电系数;α为调整系数,用于调整Kc2和Kd2曲线整体的大小,值得注意的是,α的取值并不唯一,可以根据电池储能系统的功率容量配置进行适当调整;S′0为低中间值,其值决定了Kc2曲线的变化趋势,0.1 <S′0<0.45;S′1为高中间值,其值决定了Kd2曲线 的 变 化 趋 势,0.55 <S′1<0.9。S′0取 值 为0.15、0.20、0.25、0.30、0.35、0.40 时对应的Kc2曲线,以及S′1取值为0.85、0.80、0.75、0.70、0.65、0.60 时对应的Kd2曲 线 如 附 录A 图A3 所 示。图 中,KE2为 辅 调 频控制系数。
由附录A 图A3 可知,S′0越大、S′1越小,辅调频控制的调频效果和储能SOC 恢复效果越好。但S′0太大、S′1太小,可能会导致储能SOC 很快跌出理想状态范围,储能后续的调频能力下降,同时S′0太小、S′1太大,会使辅调频控制的效果不明显。因此,S′0和S′1的取值应该适当,本文S′0取0.3,S′1取0.7。
2.2.3 储能调频阶段综合出力控制
在储能调频阶段,储能在辅调频控制动作时机图中的区域Ⅰ、Ⅵ采用变K下垂控制+辅调频控制,在区域Ⅱ、Ⅲ、Ⅳ、Ⅴ只采用变K下垂控制。由于本文构建的辅调频控制充放电系数在区域Ⅱ、Ⅲ、Ⅳ、Ⅴ取值为0,故辅调频控制在区域Ⅱ、Ⅲ、Ⅳ、Ⅴ出力也为0。因此,储能调频阶段的综合出力只需变K下垂控制出力与辅调频控制出力相加即可(虚拟下垂充放电系数与辅调频控制充放电系数相加即可得到储能调频充放电系数),而无须判断系统频率偏差和储能SOC 处于辅调频控制动作时机图中的第几区域再决定辅调频控制是否可以动作。因此,建立储能调频阶段的综合出力ΔPE与Δf的关系式如式(7)和式(8)所示。
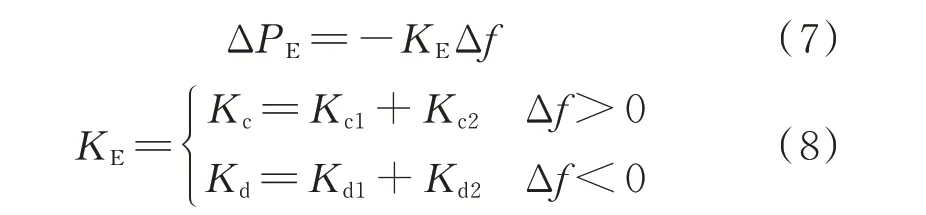
式中:KE为储能调频系数;Kc为储能调频充电系数;Kd为储能调频放电系数。
以S为自变量,建立Kc、Kd的关系式如式(9)和式(10)所示。储能调频充放电系数随S变化曲线如图3 所示。
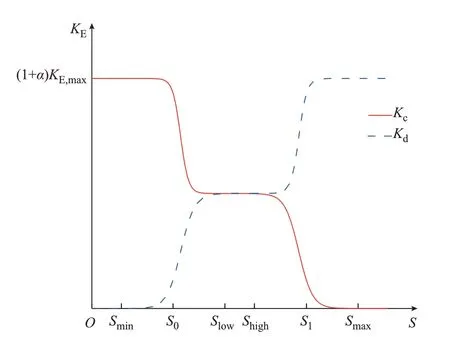
图3 储能调频系数Fig.3 Frequency regulation coefficient of BESS

2.3 储能SOC 恢复阶段出力控制
当电网调频需求不大时,即系统频率偏差在储能调频死区内时,为应对未来调频需求,对储能进行SOC 恢复控制,以保证储能SOC 处于或接近理想状态[20-21]。
从电池储能系统SOC 恢复的需求出发,对储能恢复需求系数进行建模。储能恢复需求系数构建方法如下:当储能SOC 偏低时,储能放电恢复需求系数Kd3设置为0,以免储能电量快速殆尽,而储能充电恢复需求系数Kc3设置得较大且随着储能SOC 的升高而减小;当储能SOC 偏高时,Kc3设置为0,以免储能电量快速饱和,而Kd3设置得较大且随着储能SOC 的降低而减小[14]。
以S为自变量,储能充放电恢复需求系数为因变量,采用S 型函数建立储能充放电恢复需求系数的表达式如式(11)和式(12)所示。
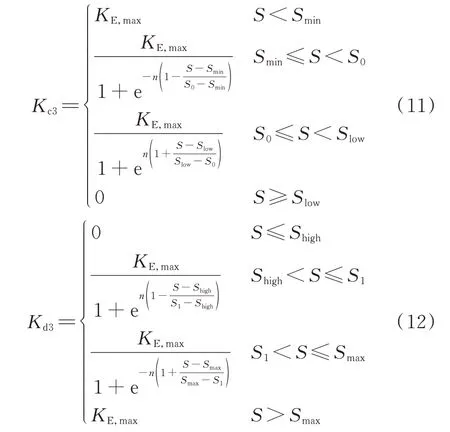
式中:S0和S1分别为储能SOC 的偏低值和偏高值。当曲线的自适应系数n取不同值时,储能恢复需求系数的变化曲线如附录A 图A4 所示。图中,KE3为储能恢复需求系数。
由附录A 图A4 可知,当n值较大时,KE3仅在很小的一段范围内跟随储能SOC 有较大变化,自适应度较弱;而当n值较小时,一定程度上影响了储能SOC 的恢复效果。因此,本文n取中间值15,在保证储能SOC 恢复效果的同时,也兼顾了KE3随储能SOC 变化的自适应性。
电池储能系统在考虑SOC 恢复需求的同时,还要保证系统频率偏差不能跌出储能调频死区,因此必须对储能恢复需求系数加以约束。
储能恢复系数约束构建方法如下:当Δfmin≤Δf<Δf0时(其中Δfmin和Δf0分别为频率偏差的最小值和偏小值),系统频率偏差接近死区下限,若此时储能有充电恢复需求,只能从电网中吸收电能,如果储能充电恢复系数约束Kc4设置得较大,则储能会吸收大量电能导致系统频率偏差跌出死区下限,故Kc4应设置得较小且随着Δf的减小而减小,若此时储能有放电恢复需求,由于系统频率偏差远离死区上限,储能即使大量放电也不会导致系统频率偏差超过死区上限,故储能放电恢复系数约束Kd4应设置得较大;当Δf0≤Δf<Δflow时(其中Δflow为频率偏差的较小值),系统频率偏差仍然距离死区下限较近,故Kc4不应设置得过大且随着Δf的减小而减小,而此时系统频率偏差仍然远离死区上限,故Kd4仍可设置得较大;当Δflow≤Δf<Δfhigh时(其中Δfhigh为频率偏差的较大值),系统频率偏差距离死区上下限都较远,故储能充放电恢复系数约束均可设置得较大;当Δfhigh≤Δf<Δf1时(其中Δf1为频率偏差的偏大值),与Δf0≤Δf<Δflow同理,Kd4不应设置得过大且随着Δf的增大而减小,而Kc4可设置得较大;当Δf1≤Δf<Δfmax时(其中Δfmax为频率偏差的最大值),与Δfmin≤Δf<Δf0同理,Kd4应设置得较小且随着Δf的增大而减小,Kc4应设置得较大[14]。
以Δf为自变量,储能充放电恢复系数约束为因变量,采用S 型函数建立储能充放电恢复系数约束的表达式如式(13)和式(14)所示。

当n取不同值时,储能恢复系数约束的变化曲线如附录A 图A5 所示。图中,KE4为储能恢复系数约束。
由附录A 图A5 可知,当n值较大时,KE4仅在很小的一段范围内跟随Δf有较大变化,自适应度较弱;而当n值较小时,可能会使系统频率偏差跌出储能调频死区。因此,本文n取中间值15,在保证系统频率偏差在储能调频死区内的同时,也兼顾了KE4随Δf变化的自适应性。
同时兼顾储能SOC 恢复需求以及电网运行状态的限制(系统频率偏差不能跌出储能调频死区),取储能恢复需求系数和储能恢复系数约束的较小值作为储能SOC 恢复系数KR,如式(15)所示。储能SOC 恢复系数曲线如图4 所示。
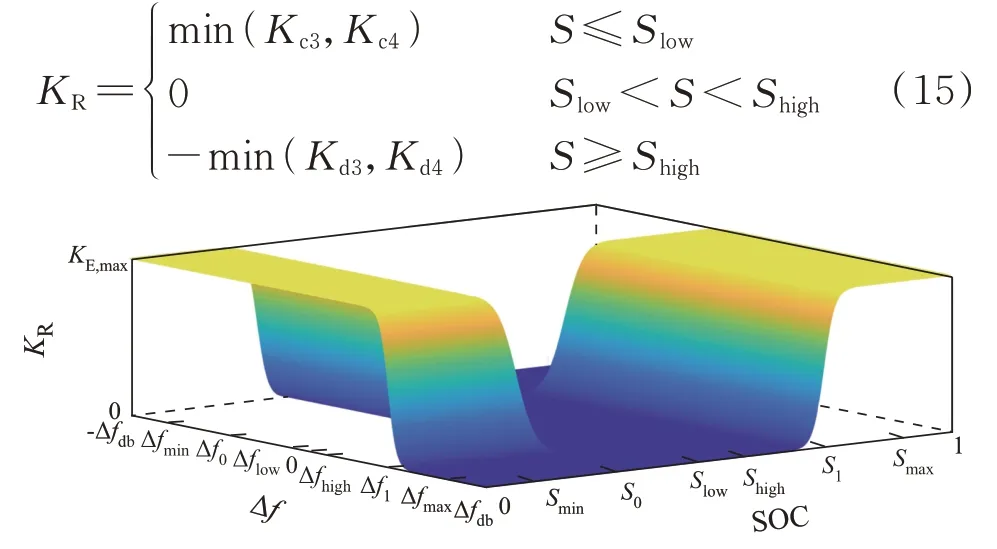
图4 储能SOC 恢复系数Fig.4 SOC recovery coefficient of BESS
综上所述,储能SOC 恢复出力ΔPR的表达式如式(16)所示。
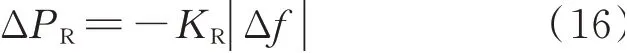
2.4 储能一次调频控制策略
结合2.2 节的储能调频阶段出力控制和2.3 节的储能SOC 恢复阶段出力控制,提出储能一次调频控制策略。储能一次调频控制策略流程图如附录A图A6 所示。
2.5 控制策略评价指标
为了定量评估和对比本文控制策略的调频效果和储能SOC 恢复效果,根据负荷扰动类型分别提出2 类评价指标。
针对阶跃负荷扰动,提出最大频率偏差Δfm和频率下降速度Vm作为评价指标。Δfm的值越小,系统频率变化幅度就越小,相对应策略的调频效果就越好;Vm的值越小,系统频率变化就越缓慢,相对应策略的调频效果就越好。
针对连续负荷扰动,提出频率偏差的均方根值Δfrms和SOC 偏差的均方根值ΔSrms作为评价指标,其中,Δfrms反映控制策略的调频效果,ΔSrms反映控制策略的储能SOC 恢复效果。表达式具体如下:
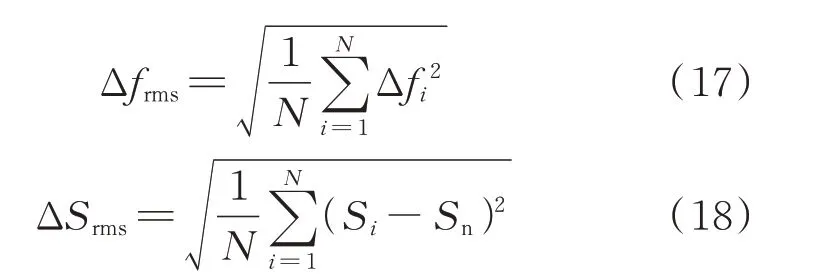
式中:Δfi为采样点i的系统频率偏差;Si为采样点i的储能SOC 值;Sn为本文设定的储能SOC 理想值,取值为0.5;N为总采样点的个数。Δfrms的值越小,电网频率波动就越小,相对应策略的调频效果就越好;ΔSrms的值越小,储能SOC 的值就越接近储能SOC 理想值,相对应策略的储能SOC 恢复效果就越好。
3 仿真分析
3.1 仿真系统参数
本文以MATLAB/Simulink 为仿真环境,搭建如图1 所示的仿真系统。其中,火电机组额定容量为1 000 MW,电池储能系统参数为15 MW/2 MW·h,火电机组一次调频的死区上下限为±0.033 Hz(标幺值为0.000 66),电池储能系统的调频死区上下限为火电机组一次调频死区上下限的60%[13](标幺值为0.000 4)。其余仿真系统参数按火电机组额定容量和电网额定频率50 Hz 为基准值进行标幺化,仿真系统参数(标幺值)如附录A 表A1 所示,控制策略的相关参数(标幺值)如附录A 表A2 所示。
3.2 控制策略对比仿真分析
在2 种典型工况(阶跃负荷扰动工况、连续负荷扰动工况)下,采用控制变量法将本文所提控制策略(2.2.3 节+2.3 节)与无储能和变K下垂[12]+SOC 恢复控制策略(2.2.1 节+2.3 节)进行对比仿真,来验证本文所提控制策略的有效性和优越性。
3.2.1 阶跃负荷扰动工况仿真分析
在仿真模型中的3 s 时刻加入幅值标幺值为0.02 的阶跃负荷扰动,电池储能系统的初始SOC 设置为0.8,仿真时长设置为60 s。阶跃负荷扰动下的频率偏差变化曲线、储能出力曲线和SOC 变化曲线如图5 所示,相应评价指标如表1 所示。
由图5(a)可知,在3 s 加入阶跃扰动后,3 种调频控制策略所对应的频率偏差都快速下降,其中,无储能控制方式的频率偏差下降最快,最大频率偏差也最大。由表1 可知,本文策略的最大频率偏差Δfm比无储能小58.84%,频率下降速度Vm比无储能小62.73%,可见引入储能可以有效改善频率响应效果。同时,从图5(a)的局部放大图中可以看出,本文策略的最大频率偏差比变K下垂+SOC 恢复策略的小,并且到达最大频率偏差的时刻也更晚,表明本文策略的调频效果更优。本文策略在储能SOC偏高时具有更大的储能调频放电系数,故本文策略的储能出力比变K下垂+SOC 恢复策略的储能出力更大,但由于储能受额定功率的限制,导致储能无法提供更多的调频出力,故本文策略与变K下垂+SOC 恢复策略的最大频率偏差相差不大。
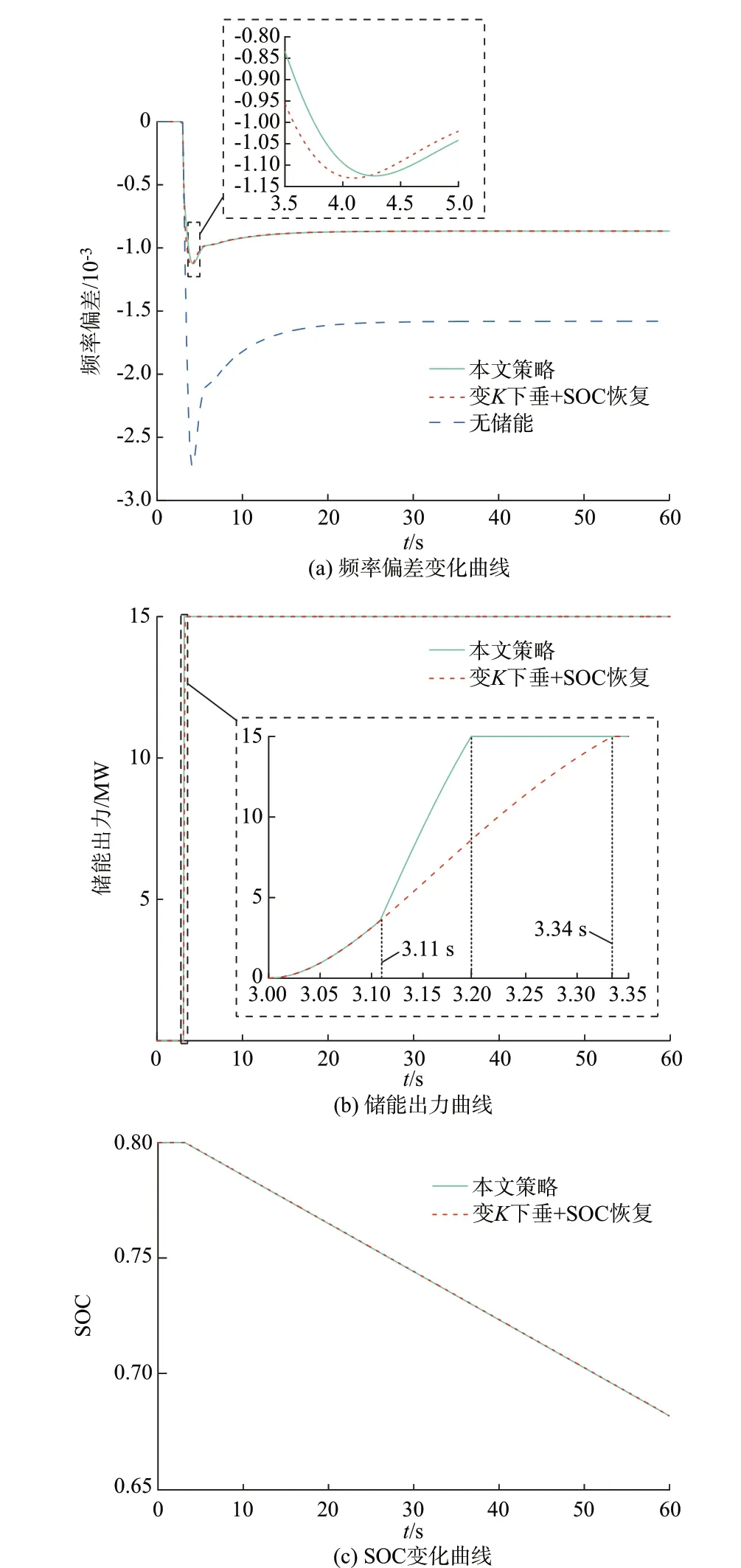
图5 阶跃负荷扰动下的频率偏差变化、储能出力、SOC 变化曲线Fig.5 Curves of frequency deviation variation,output power of BESS and SOC variation with step load disturbance

表1 阶跃负荷扰动下的调频评价指标Table 1 Evaluation index of frequency regulation with step load disturbance
由图5(b)可知,2 种策略的储能出力在阶跃扰动发生后都快速由0 上升到储能的最大出力15 MW,充分体现了储能调频的快速响应特性。同时,从图5(b)的局部放大图中可以看出,从3.11~3.34 s 这一阶段,本文策略的储能出力一直大于变K下垂+SOC 恢复策略的储能出力,且本文策略的储能出力更快到达最大值,故本文策略的最大频率偏差更小,并且频率下降速度也更慢。
由表1 可知,本文策略的Δfm比变K下垂+SOC恢复策略小0.44%,Vm比变K下垂+SOC 恢复策略小13.73%,可见,本文策略的调频效果略好于对比策 略。由 图5(c)可 知,2 种 策 略 的 储 能SOC 消 耗相同。
综上所述,在阶跃负荷扰动工况下,本文策略能够有效改善频率响应效果,并且调频效果略好于变K下 垂+SOC 恢 复 策 略。
3.2.2 连续负荷扰动工况仿真分析
在仿真模型中加入幅值标幺值为0.025 的连续负荷扰动,即连续负荷扰动在(-0.025,0.025)内波动,电池储能系统的初始SOC 设置为0.15,仿真时长设置为10 min。连续负荷扰动下的频率偏差变化曲线、SOC 变化曲线和储能出力曲线如图6 所示,相应评价指标如表2 所示。
由图6(a)和表2 可知,无储能的频率偏差波动幅度最大且本文策略的频率偏差的均方根值Δfrms比无储能小64.97%,充分说明了储能可以有效减小频率波动。将图6(a)的频率偏差分为正频率偏差和负频率偏差(正频率偏差对应储能充电出力和储能充电调频效果,负频率偏差对应储能放电出力和储能放电调频效果)。可以看出,本文策略和变K下垂+SOC 恢复策略的正频率偏差均小于无储能的正频率偏差,且本文策略的正频率偏差更小,说明本文策略在储能SOC 偏低时,提升了储能的充电调频效果;而本文策略和变K下垂+SOC 恢复策略的负频率偏差与无储能的负频率偏差相差并没有像正频率偏差相差得那么大,且在前半段时间内,本文策略与变K下垂+SOC 恢复策略的负频率偏差几乎相同,但在后半段时间内,本文策略的负频率偏差更小。由此可见,本文策略改善了储能的放电调频效果,在一定程度上解决了储能SOC 偏低时储能放电调频能力不足的问题。

表2 连续负荷扰动下的调频评价指标Table 2 Evaluation index of frequency regulation with continuous load disturbance

图6 连续负荷扰动下的频率偏差变化、SOC 变化、储能出力曲线Fig.6 Curves of frequency deviation variation,SOC variation and output power of BESS with continuous load disturbance
由图6(b)可知,本文策略的储能SOC 比变K下垂+SOC 恢复策略恢复更快,表明本文策略在储能SOC 偏低时,可以使储能SOC 更快地恢复到较好的状态。
由图6(c)可知,本文策略的储能充电出力(储能出力小于0 表示储能充电)比变K下垂+SOC 恢复策略的储能充电出力大,这是由于储能SOC 偏低时,辅调频控制发挥作用,使得本文策略的储能调频充电系数更大,故储能充电出力更大,进而导致本文策略的正频率偏差更小,储能充电更快,储能SOC恢复得也更快。同时,为了防止储能SOC 快速殆尽而影响储能循环寿命,在储能开始调频时,2 种策略的储能放电出力都接近于0,随着储能SOC 的恢复,2 种策略的储能放电出力开始慢慢增大,由于本文策略的储能SOC 恢复更快,储能调频放电系数也更大,故本文策略的储能放电出力逐渐大于变K下垂+SOC 恢复策略的储能放电出力,使得本文策略在储能调频后半段时间内的负频率偏差更小。
由表2 可知,本文策略的频率偏差均方根值Δfrms比变K下垂+SOC 恢复 策略小3.37%,SOC 偏差的均方根值ΔSrms比变K下垂+SOC 恢复策略小2.54%。可见,本文策略具有更好的调频效果以及储能SOC 恢复效果。
为验证本文采用的储能SOC 恢复出力控制的有效性和优越性,将本文所提控制策略(2.2.3 节+2.3 节)与仅有调频控制无储能SOC 恢复(2.2.3 节)和调频控制+SOC 恢复控制策略[14](2.2.3 节+文献[14]采用的SOC 恢复控制策略)进行对比仿真。3 种策略下的SOC 变化曲线如附录A 图A7 所示。
由附录A 图A7 可知,本文策略的SOC 变化曲线比调频控制无SOC 恢复与调频控制+SOC 恢复[14]的曲线更接近SOC 的理想状态,说明本文采用的储能SOC 恢复出力控制能够有效调整储能SOC,使得SOC 变化曲线向理想状态偏移,并且可以使储能SOC 更快恢复。经计算,本文采用的储能SOC 恢复出力控制使储能恢复0.108 MW·h 的电量,恢复电量十分可观,这部分电量在一定程度上可以使储能SOC 更接近理想状态,以更好地应对下一阶段的调频任务;而文献[14]采用的SOC 恢复控制策略仅使储能恢复0.038 MW·h 的电量,说明本文采用的储能SOC 恢复出力控制具有更好的储能SOC 恢复效果。
综上所述,在连续负荷扰动工况下,本文策略可以有效减小电网频率波动,并能使储能SOC 更快地恢复到较好的状态,在一定程度上解决了储能SOC偏低或偏高时储能充放电调频能力不足的问题,并且能有效调整储能SOC,使储能SOC 更接近理想状态。同时,与对比策略相比,还具有更好的调频效果以及储能SOC 恢复效果。
4 结语
本文针对储能SOC 偏低或偏高时储能充放电调频能力不足的问题,提出一种考虑SOC 恢复的储能一次调频控制策略。仿真结果表明,本文提出的储能一次调频控制策略具有以下优势:
1)在阶跃负荷扰动工况下,本文策略能够有效改善频率响应效果,最大频率偏差Δfm与频率下降速度Vm分别比变K下垂+SOC 恢复策略小0.44%和13.73%,调频效果略好于对比策略。
2)在连续负荷扰动工况下,本文策略能够有效减小频率波动,并能使储能SOC 更快地恢复到较好的状态,在一定程度上解决了储能SOC 偏低或偏高时储能充放电调频能力不足的问题,频率偏差的均方根值Δfrms与SOC 偏差的均方根值ΔSrms分别比变K下垂+SOC 恢复策略小3.37%和2.54%,具有更好的调频效果以及储能SOC 恢复效果。
3)在连续负荷扰动工况下,本文采用的储能SOC 恢复出力控制可以有效对储能SOC 进行恢复,使储能SOC 更接近理想状态,以提高储能下一阶段的调频能力,同时与对比策略相比,还具有更好的储能SOC 恢复效果。
电池储能系统不仅可以辅助电网调频,还可以辅助电网进行削峰填谷,如何充分利用电池储能系统,设计合理的储能调频/调峰策略以保证电池储能系统调频和调峰的协调配合还有待进一步研究。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

