主辅电力市场外部性价值优化定价方法
刘 硕,王剑晓,宋懿洋,陈启鑫,杨知方,夏 清
(1. 新型电力系统运行与控制全国重点实验室,清华大学电机工程与应用电子技术系,北京市 100084;2. 北京电力交易中心有限公司,北京市 100031;3. 大数据分析与应用技术国家工程实验室,北京大学,北京市 100871;4. 新能源电力系统国家重点实验室,华北电力大学电气与电子工程学院,北京市 102206;
5. 重庆大学电气工程学院,重庆市 400044)
0 引言
2022 年,《关于加快建设全国统一电力市场体系的指导意见》[1]发布。意见指出,加快建设国家电力市场,推进适应能源结构转型的电力市场机制建设。因此,为了逐步增强市场在电力资源优化配置中的作用,促进“碳达峰·碳中和”工作的全面部署[2],以市场化手段解决负荷及新能源的能量及辅助服务需求问题是迎合当今中国电力市场深化改革的必然要求,如何构建能够量化市场成员外部性价值的电能量及备用市场机制成为当前的研究重点。
目前,边际价格交易机制普遍应用于国内外电力市场[3],理论上,其能够以市场手段提高电力资源使用效率,然而,实践证明边际价格交易机制仍面临多方面的挑战[4-6]。随着能源结构转型,越来越多的可再生能源并入电网带来了大量的备用容量需求[7]。与此同时,备用市场与能量市场耦合紧密,而边际价格交易机制下的火电机组有意愿对其提供的能量及辅助服务虚报高价,导致市场行为异常。现有市场机制难以量化市场成员的外部性价值[8],为精准辨识市场成员价值,更多的学者专注于研究满足激励相容性质的市场机制。文献[9]将Vickey-Clarke-Groves(VCG)机制应用于电力市场,精准评估市场成员所创造的价值。文献[10]对比分析了边际价格机制和VCG 机制,证明了边际节点平均电价低于VCG 机制节点平均电价。文献[11]证明了VCG 机制满足激励相容、成本最小化和个体理性。文献[12]提出了信息租金的分摊机制,使得VCG 机制能满足收支平衡。为了有效促进市场成员真实报价,本文采用VCG 机制,基于替代效益[13]精确辨识火电机组为新能源及负荷提供的能量与辅助服务价值。
与现有电力市场广泛应用的边际价格机制相比,VCG 机制虽然满足了激励相容性质,但计算效率却不高。边际价格机制只需1 次出清即可实现对所有市场成员的结算[14];而VCG 机制需要分别移除所有市场成员,并在每次移除后都需要进行1 次优化出清,即对N台发电机组进行N+1 次优化出清,计算效率明显降低。本文针对VCG 机制求解效率低的问题,在基于单纯形法求解过程中,约束条件的右端项改变时检验数不发生改变[15]的结论,提出了基于最优基替换的加速算法。对市场成员真实成本的辨识方法进行了改进。基于IEEE 57 节点系统和IEEE 118 节点系统,验证了所提算法的有效性。本文的主要贡献如下。
1)面对负荷的波动及新能源的高比例并网,本文提出主辅电力市场外部性价值优化定价方法,精确辨识新能源及负荷的外部性价值。其中,新能源外部性价值的精确辨识对指导新能源价格申报、促进绿色电力参与交易意义重大。
2)本文提出基于最优基替换的快速求解算法,相比于对新问题重新求解,可以在初始问题最优基的基础上进行热启动,有效利用初始问题最优解,提高VCG 机制的计算效率。
1 系统模型
随着电力系统中新能源发电的渗透率不断提高,市场主体应当为新能源提供更为全面的辅助服务以应对新能源并网带来的备用需求[16]。为此,本文将可再生能源纳入市场出清模型,构建计及负荷和新能源的主辅电力市场出清模型。以火电机组发电成本及旋转备用成本最小为目标函数,考虑潮流约束、负荷平衡约束、机组运行约束等。采用直流潮流进行计算。
1)目标函数
本文将备用容量细化为上旋转备用和下旋转备用,火电机组通过调度上、下旋转备用分别满足高峰负荷及低谷负荷,考虑发电成本和备用容量调度成本的目标函数如下:
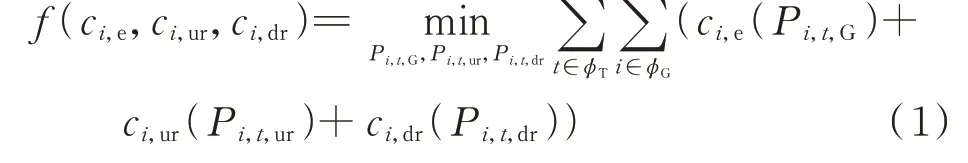
式中:f(ci,e,ci,ur,ci,dr)为火电机组发电成本及旋转备用成本总和;ϕT为量测时刻集合;ϕG为火电机组集合;ci,e、ci,ur、ci,dr分别为火电机组的发电成本、上调旋转 备 用 成 本 以 及 下 调 旋 转 备 用 成 本;Pi,t,G为t时 刻火 电 机 组i的 有 功 出 力;Pi,t,ur为t时 刻 火 电 机 组i提供的上调旋转备用容量,包括为负荷提供上调旋转备用和为新能源机组提供上调旋转备用;Pi,t,dr为t时刻火电机组i提供的下调旋转备用容量,包括为负荷提供的下调旋转备用和为新能源机组提供的下调旋转备用。
2)系统约束
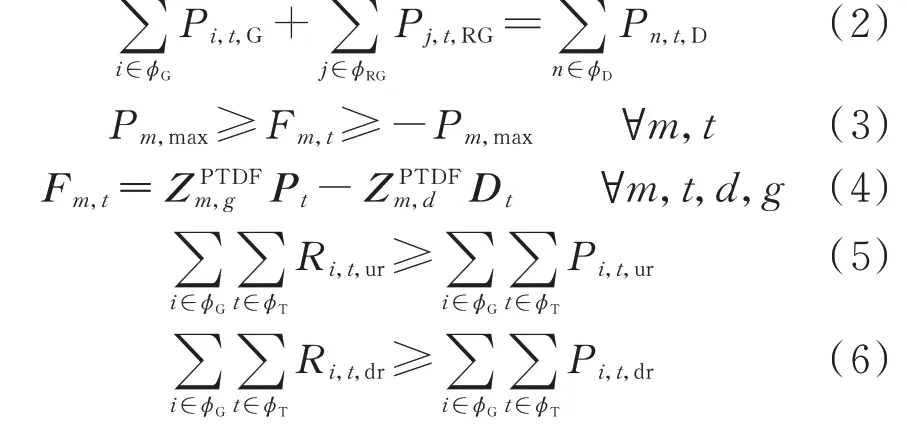
式中:ϕRG为可再生能源机组集合;ϕD为负荷集合;Pj,t,RG为t时 刻 可 再 生 能 源 机 组j的 有 功 出 力;Pn,t,D为t时刻负荷n的有功需求;Pm,max为输电线路m断面潮流功率限制;Fm,t为t时刻输电线路m的传输功率;ZPTDFm,g为机组g到输电线路m的潮流灵敏度分布因子矩阵;ZPTDFm,d为负荷d到输电线路m的潮流灵敏度分布因子矩阵;Pt为t时刻机组出力计划矩阵,包括火电机组和新能源机组的出力计划;Dt为t时刻系 统 负 荷 需 求 矩 阵;Ri,t,ur和Ri,t,dr分 别 为 火 电 机 组i在t时刻申报的上调和下调备用容量供给能力。
其中,式(2)是系统功率平衡约束;式(3)是线路热稳定约束;式(4)是输电线路潮流计算公式;式(5)和式(6)分别为系统的上、下备用容量约束。
3)火电机组有功出力约束
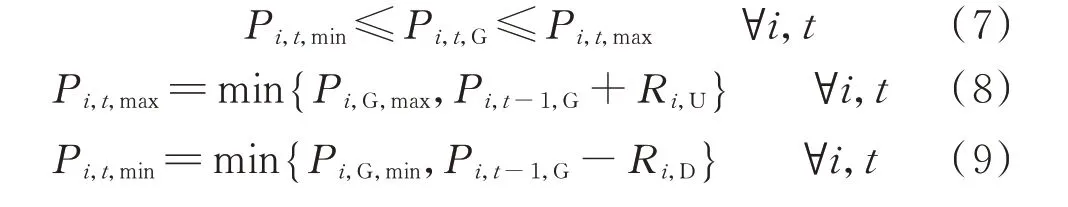
式 中:Pi,t,max为t时 刻 火 电 机 组i输 出 有 功 功 率 上 限;Pi,t,min为t时 刻 火 电 机 组i输 出 有 功 功 率 下 限;Pi,G,max和Pi,G,min分 别 为 火 电 机 组i最 大 有 功 出 力 和 最 小 有功 出 力;Pi,t-1,G为 时 刻t的 前 一 时 刻 火 电 机 组i的 有功 出 力;Ri,U和Ri,D分 别 为 火 电 机 组i的 向 上 爬 坡 功率最大值和向下爬坡功率最大值。
式(7)为t时刻火电机组i有功出力的最大、最小约束;式(8)为t时刻火电机组i输出有功功率上限的计算公式;式(9)为t时刻火电机组i输出有功功率下限的计算公式。
4)火电机组备用约束
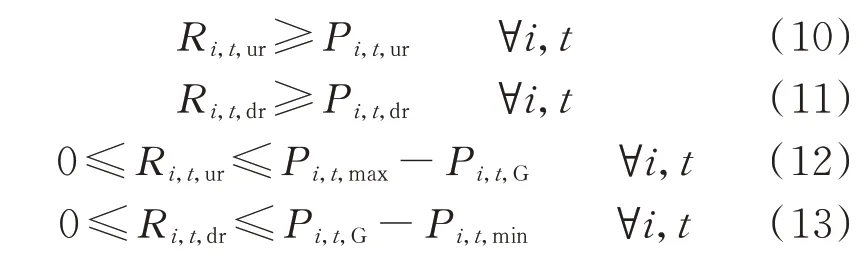
式(10)—式(13)为火电机组备用约束。火电机组为负荷和新能源机组提供备用容量且火电机组申报的备用容量供给能力不小于新能源机组和系统负荷的备用需求总和。其中,式(10)和式(12)为t时刻火电机组i的上旋转备用约束;式(11)和式(13)为t时刻火电机组i的下旋转备用约束。
5)火电机组爬坡约束
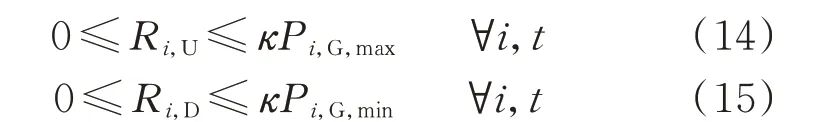
式中:κ为火电机组爬坡容量系数。
其中,式(14)为机组i的上爬坡约束;式(15)为机组i的下爬坡约束。
6)可再生能源约束
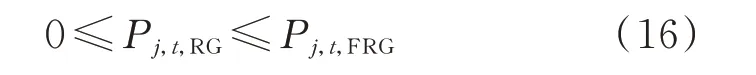
式 中:Pj,t,FRG为t时 刻 可 再 生 能 源 机 组j的 有 功 出 力预测值。
式(16)表示新能源机组有功出力的预测值为其有功出力最大值。式(1)—式(16)可以被写成如下矩阵形式:
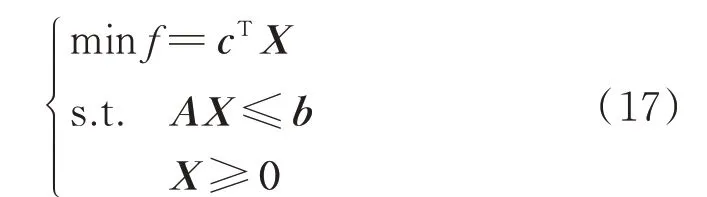
式中:c为成本系数向量;X为决策变量向量,包括火电机组出力、火电机组上调旋转备用容量和下调旋转备用容量;A为约束条件的系数矩阵;b为约束条件右端项。
式(17)中c、A、b均与式(1)—式(16)中的系数相对应。在主辅电力市场中,对于向新能源和负荷提供备用的火电机组辅助服务定价问题,应先获取火电机组所申报的能量、上旋转备用容量和下旋转备用容量的成本系数,随后求解电力市场优化出清模型,得到火电机组的计划出力和上、下旋转备用容量,最终基于VCG 机制,得到运营商需要向火电机组支付的费用。
2 外部性定价机制设计
本文研究以系统容量充足为前提,即任意一台发电机组的缺失都不会导致优化出清模型中可行解的缺失。考虑到市场供需关系对外部性定价机制的影响,在实际应用中,可通过切除一定量负荷或将储能资源纳入新型电力系统需求响应以应对供需紧张问题。
2.1 基于VCG 的外部性定价机制原理
在基于VCG 的外部性定价机制中,市场成员的价值被定义为该市场成员对其他市场成员的替代效益[13]。文献[11]从成本最小化、个体理性和激励相容等方面量化评价了该机制的可行性,VCG 机制满足成本最小化、个体理性和激励相容。其中,成本最小化对应了电力系统经济调度的优化结果;个体理性保证了市场成员参与电力日前市场的积极性;激励相容性质促进了市场成员的真实报价。
文献[17]指出:任何一种市场机制都不能同时满足成本最小化、个体理性、激励相容和收支平衡4 种性质。而VCG 机制不满足收支平衡性质,针对VCG 机制不满足收支平衡性质,采用信息租金的分摊机制[12]以解决收支不平衡的问题,信息租金可被分别分摊至可再生能源、所有时刻负荷以及尖峰时刻负荷,以促使VCG 机制满足收支平衡性质。特别地,当信息费用被分摊至高峰负荷时,高峰负荷被削减,这将有利于进一步促进用户侧的需求响应。需要说明的是,在外部性定价机制下,运营商为激励火电机组真实报价支付了信息租金,这笔费用引起的电价上涨要远小于火电机组策略性报价时引起的市场效率损失。
VCG 机制基于市场成员对其他成员的替代效益定义了市场成员的价值[18]。发电机组的价值决定了其获得的系统调度支付,系统中发电机组i获得的系统调度支付可表示为:
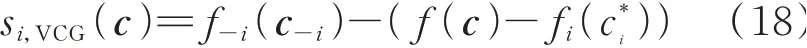
式中:si,VCG(c)为发电机组i获得的系统调度支付;f-i(c-i)为发电机组i被移除市场后剩余发电机组的总成本;f(c)为移除发电机组i之前所有发电机组的总成本;fi(c*i)为发电机组i在最优出力时的发电成本。
式(18)表示基于VCG 的外部性定价机制下发电机组i的定价方式,等号右边两项相减即为发电机组i被移除市场前后其他发电机组的成本变化量,反映了发电机组i对其他发电机组的替代效益。
基于VCG 的外部性定价机制利用市场成员之间的替代效益,定义了发电机组报价方式,实现了市场成员与市场整体利益的一致性,有效促进了市场成员的真实报价。
2.2 边际价格机制与VCG 定价机制案例对比
本节引入两节点两机组系统案例,通过对比发电机组1 虚假申报和真实申报时机组1 净利润的变化,分析得出边际价格机制和基于VCG 的外部性定价机制的效果差异。两节点两机组系统如图1所示。
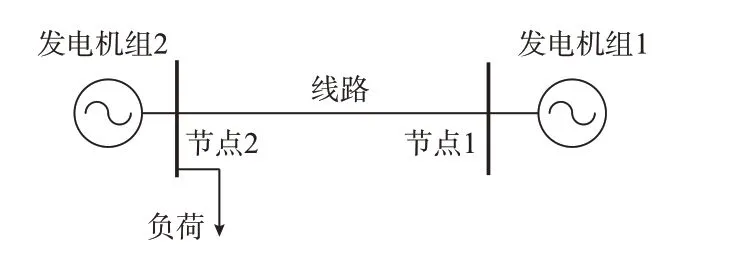
图1 两节点两机组系统结构Fig.1 Structure of a 2-bus 2-generator-unit system
在本案例中,发电机组1 和2 的真实成本系数分别为2c′和3c′,两节点之间线路容量为0.5D′,负荷为0.5D′,发电机组出力范围为[0,2D′]。其中,c′和D′分别为成本系数基值和容量基值。
对于边际价格机制,综合考虑式(1)—式(4),在发电机组1 和2 真实申报成本系数下的出力计划为:
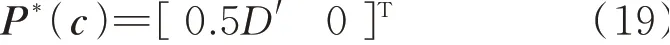
式中:P*(c)为发电机组申报真实成本系数下的出力计划。
此时,节点1 的节点电价为2c′,发电机组1 和2的净利润均为0。当发电机组1 虚报价格为3c′,此时发电机组出力计划如式(20)所示,发电机组1 收益变为0.25D′c′,且大于真实申报时的收益。因此,发电机组有意愿虚报高价,提高自身收益。
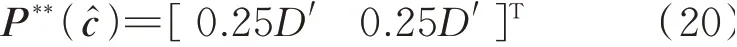
式中:P**(ĉ)为发电机组申报虚假成本ĉ时的出力计划,此时,发电机组出力计划P**(ĉ)已经偏离最优出力计划P*(c)。
可见,在边际价格机制下,机组虚假报价有可能导致机组出力偏离最优出力计划,此时系统发电成本增加,难以实现系统成本最小化。
对于基于VCG 的外部性定价机制,以机组1 为例,当发电机组1 和2 申报真实成本系数时,发电机组1 的净利润为0.5D′c′;当发电机组1 提高申报成本系数至3c′时,机组出力计划变为式(20),此时发电机组1 的净利润为0.25D′c′。可以看出,发电机组1在真实申报时得到的净利润大于虚假申报时的净利润,申报真实成本为其最优申报策略。因此,基于VCG 的外部性定价机制能有效抑制发电机组的策略性报价行为。
3 基于最优基替换的加速算法
3.1 加速算法设计
VCG 机制下,计算市场成员真实支付时应首先计算市场中N台发电机组总成本及发电机组i最优出力时的成本,二者分别对应式(18)中的f(c)和fi()。然后,移除发电机组i并重新进行市场出清,即获得火电机组为市场成员提供的能量及辅助服务的报价时,需要对N个市场成员进行N+1 次优化计算,与边际价格机制相比,计算效率较低。VCG机制未能有效利用第1 次的计算结果,造成了计算资源的浪费。因此,如何提升VCG 机制的优化计算效率成为其在电力市场应用中的关键。
在进行电力市场出清时,移除1 台发电机组i的操 作 等 价 于 将 原 市 场 出 清 模 型 中Pi,G,max设 置 为0,即改变式(17)中约束条件的右端项,右端项的改变不会引起求解过程中检验数的变化,故所有机组未被移除时的原问题最优基B可作为机组i被移除后的初始可行基。依据该性质,本节充分利用初次优化的最优解,在移除发电机组后使用对偶单纯形法在原问题最优基的基础上进行热启动,提出基于最优基替换的加速算法,对市场成员真实报价的计算方法进行改进。
加速算法利用对偶单纯形法,在原问题最优基的基础上继续进行最优基变换;传统的逐次优化算法则需要对新问题进行重新求解。基于最优基替换的加速算法有效利用了原问题的出清结果及最优基,显著提高了求解效率,其具体过程如下。
1)对N台发电机组进行优化出清,得到N台发电机组总成本f(c)和待定价机组i的成本fi(c*i),二者相减得到式(18)中的部分优化结果,其中原市场出清模型的最优解见式(21)。
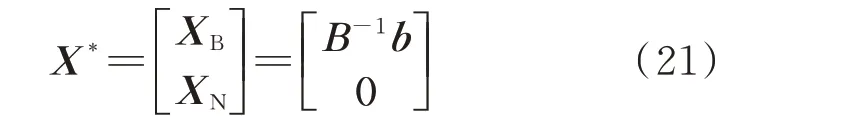
式中:XB为基变量,包括中标发电机组的出力以及非零的松弛变量和辅助变量;XN为非基变量,包括未中标的发电机组出力以及数值为0 的松弛变量和辅助变量;X*为原市场出清模型式(17)的最优解。
2)移除发电机组i,此时式(17)中b发生变化,即b'=b+Δb,Δb如式(22)所示,由于原问题最优基可当作新问题初始可行基继续使用,新问题可由式(23)和式(24)求解,最终得到N-1 台发电机组的出清结果。
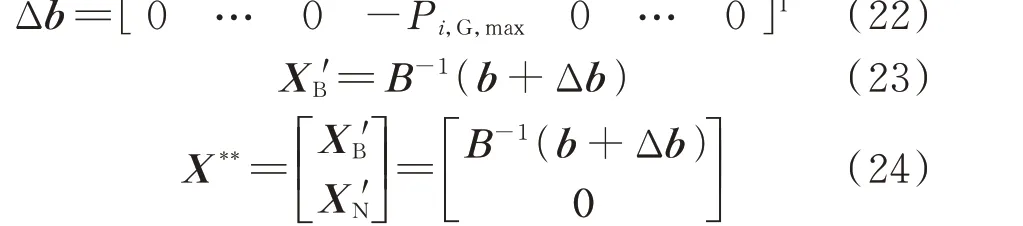
式中:Δb为约束条件右端项变化量;X'B为新基变量,由新问题中标发电机组出力以及非零的松弛变量和辅助变量组成;X'N为新非基变量,由新问题中未中标的发电机组出力以及数值为0 的松弛变量和辅助变量组成;X**为新市场出清模型的最优解。
3)判断新问题的初始解X**是否非负。若X**非负,则X**为新问题的最优解,X'B包含新问题里中标发电机组的最优出力;若X**存在小于0 的情况,则说明发电机组i在原问题的电力市场中未中标,应继续通过对偶单纯形法[19]寻找最优解,使用对偶单纯形法寻优的具体步骤如下。
步骤1:检查式(17)中约束的右端项b和单纯形表中的检验数。当右端项b非负且检验数均为非正,表明已达到最优解,此时可停止计算;当右端项b存在负数且检验数均非正,则按步骤2 和步骤3 确定换出、换入变量。
步骤2:确定换入变量。由式(25)计算(B-1b)l,(B-1b)l对应的xl为待换出基变量。
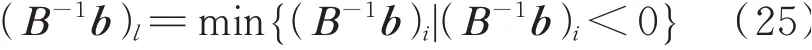
步骤3:确定换入变量。若xl所在行的所有系数alh均大于等于0,则无可行解;若存在alh小于0,则按θ规则[20]确定换入变量,θ规则如式(26)所示。
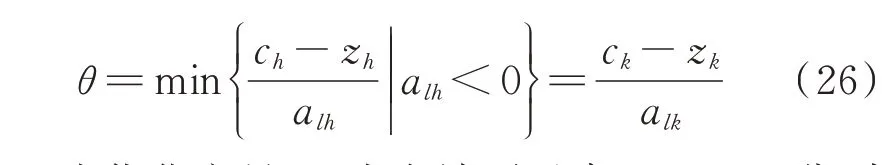
式中:θ为优化变量;zh为右端项元素;ck、zk、alk分别为待换入变量xk所在行的成本系数、右端项以及所有不等式系数。
步骤4:利用单纯形法,以alk为主元素进行迭代计算,重复步骤1 到步骤4,直至得到最优解或无可行解。
3.2 案例说明
为了说明在VCG 机制下与需要逐次移除机组的原始出清算法相比,基于最优基替换的加速算法在计算效率上的优越性,采用如式(27)所示的模型说明。
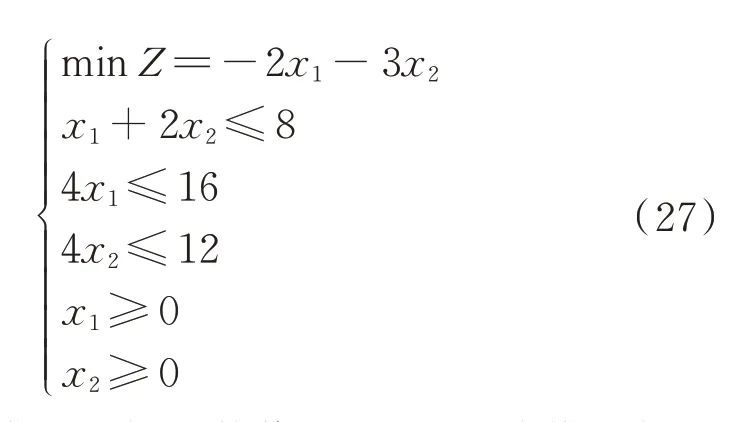
式中:Z为该模型目标函数值;x1和x2为该模型优化变量。
对于式(27),现引入正松弛变量x3、x4和x5,将式(27)转化为标准型,并将约束条件右端项中的16设置为0,这表示将变量x1设置为0,此时Δb=[0,-16,0]T。引入Δb和松弛变量后的标准型如式(28)所示。
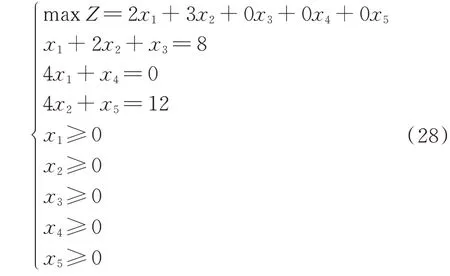
首先,对原问题进行优化出清,得到原问题最优解及其最优基;然后,将变量x1设置为0,分别用逐次优化的传统算法和基于最优基替换的加速算法,计算移除变量x1后变量x2的最优解,并对比2 种算法的寻基效率。
1)在变量x1被移除之前,对原问题优化出清,在本次结算过程中,得到了变量x1、x2的最优解,实现了从[x3,x4,x5]到[x1,x5,x2]的基变换。
2)设置变量x1为0 后,对于VCG 机制下原始的电力市场优化出清问题,需要从初始可行基[x3,x4,x5]重新计算,经过4 次基变换,得到最优基[x1,x3,x2],传统结算方式的寻基过程如图2 所示。
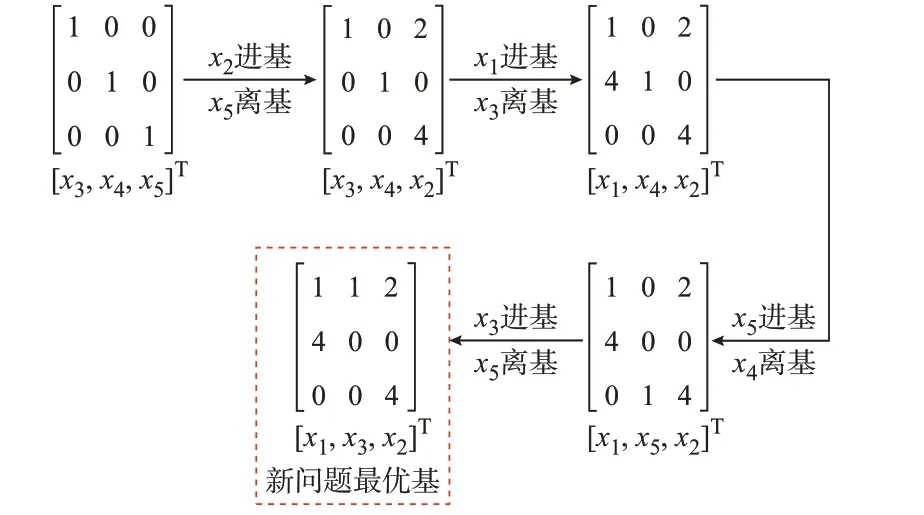
图2 传统算法的寻基过程Fig.2 Base-finding process for traditional algorithm
3)对于基于最优基替换的加速算法,利用右端项改变时检验数的不变性,原问题的最优基就是新问题的初始可行基,针对式(28),等号两端同时乘以B-1得到新的X'B,如式(29)所示。
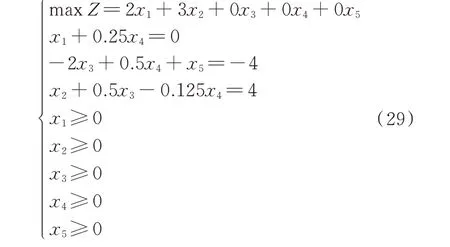
由于X**中存在小于0 的值-4,因此原问题的最优基[x1,x5,x2]不是新问题的最优基,此时选择b中最小值对应的基变量x5作为离基变量,按照最小比值规则[21]选择进基变量,完成1 次基变换,变换结果见式(30),此时b全部非负,则此时[x1,x3,x2]为最优基。
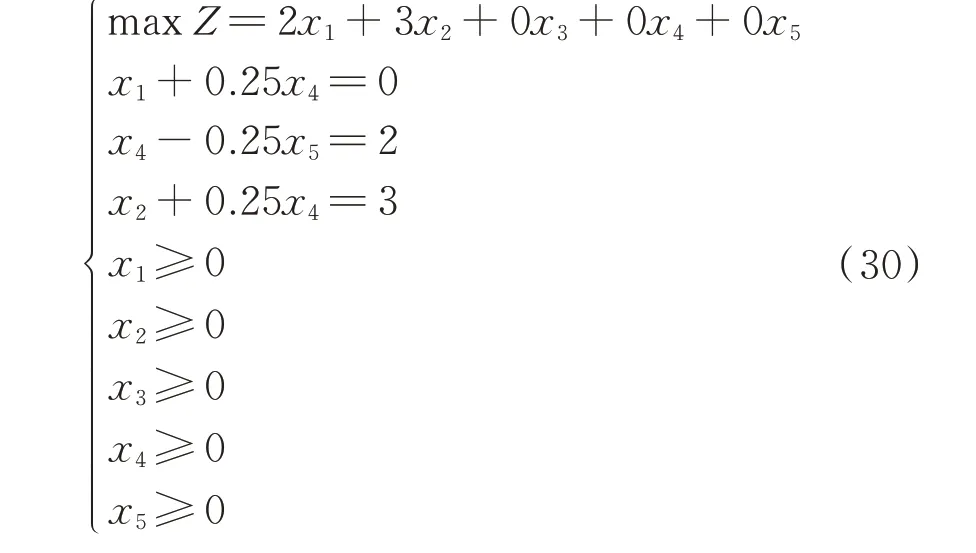
对于本案例,使用加速算法时,公式等号两端同乘B-1的操作可等价于选择原问题的最优基作为新问题的初始可行基,经过1 次基变换得到新问题的最优基,其寻基过程如图3 所示。
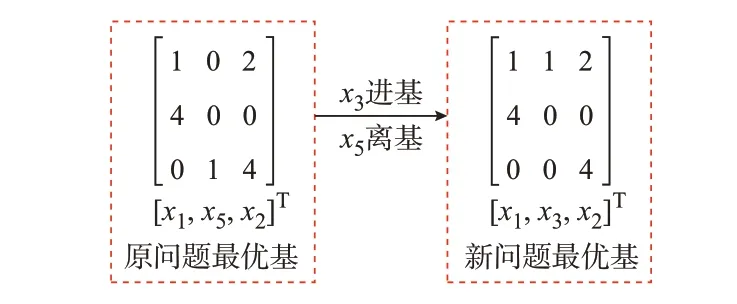
图3 基于最优基替换的加速算法寻基过程Fig.3 Base-finding process for accelerated algorithm based on optimal base substitution
通过对本案例的分析:若选择原问题最优基变量作为新问题初始基变量,只需进行1 次换基即可得到新问题最优基;若利用传统算法对新问题进行重新优化出清则需要4 次换基。可见,基于最优基替换的加速算法显著提高了优化计算效率。
4 算例分析
本文应用IEEE 57 节点系统和IEEE 118 节点系统验证VCG 机制下基于最优基替换的加速算法的有效性,基于IEEE 57 节点系统算例计算可再生能源的外部性成本并验证VCG 机制是否满足占优策略的激励相容性质。本文所涉及算例的测试环境均为2.5 GHz CPU、8 GB RAM 的笔记本电脑,使用MATPOWER 6.0[22]作为潮流计算求解器,潮流优化 计 算 工 具 为IBM ILOG CPLEX 12.6[23],编 程 平台为MATLAB R2016a。
4.1 IEEE 57 节点系统
IEEE 57 节 点 系 统 共 包 含80 条 线 路、7 台 火 电机组,算例的相关参数及系统拓扑结构均参照IEEE 57 节点标准系统参数设置,火电机组相关参数见表1。
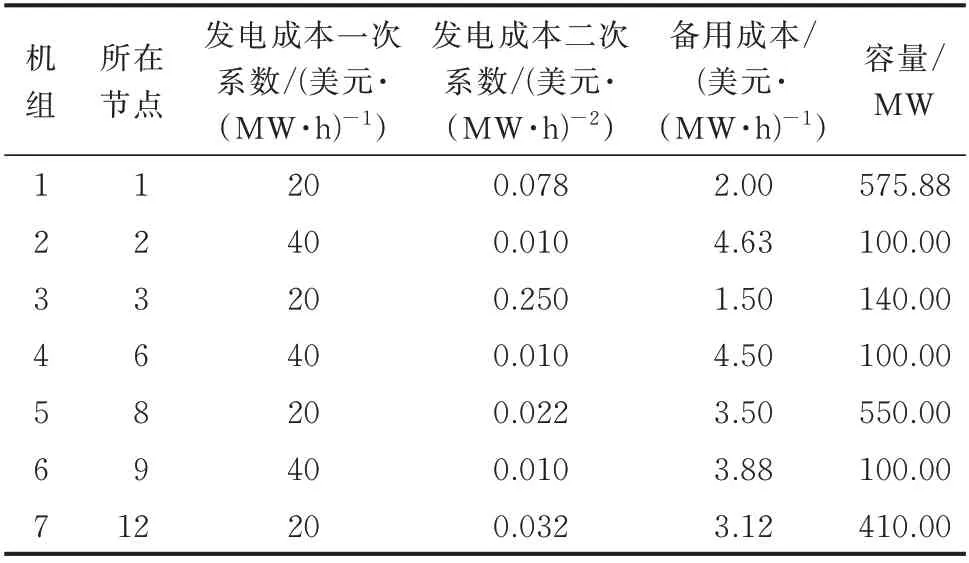
表1 火电机组参数Table 1 Parameters of thermal power units
4.1.1 新能源外部性成本计算
在IEEE 57 节点系统算例中加入4 台新能源机组,分别在节点6、9 设置风电机组1、2,在节点41、56 设置光伏电站3、4,新能源机组的装机容量均为50 MW。
如表2 所示,本文采用VCG 机制计算新能源并入电网的外部性价值。通过计算新能源机组并入电网前后火电机组成本的变化量,量化了新能源并入电网的外部性价值。算例涉及的新能源数据均来自美国国家能源实验室。
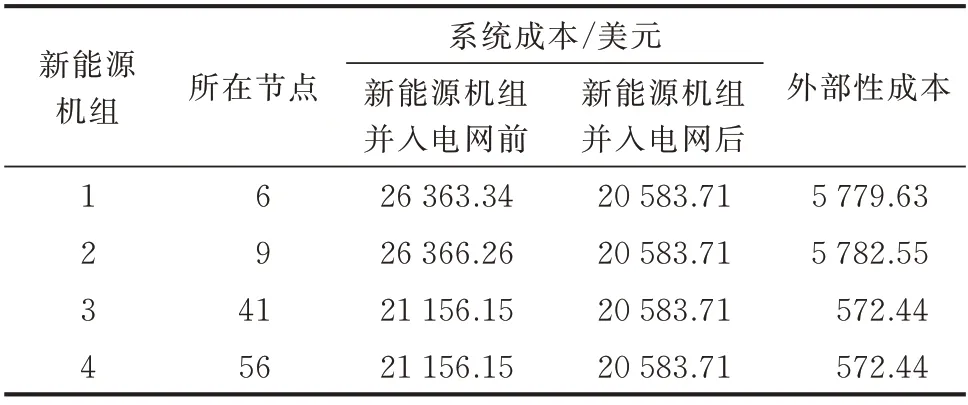
表2 IEEE 57 节点系统中新能源机组外部性价值计算Table 1 Calculation of externality value of renewable energy units in IEEE 57-bus system
4.1.2 VCG 机制下激励相容性质验证
在IEEE 57 节点系统的算例中,为验证参与调度的7 台火电机组是否满足占优策略的激励相容性质,本文对比了火电机组申报不同备用成本时净利润的变化情况。火电机组净利润最大在图中表示为净利润比例等于1。
如图4 所示,以火电机组7 为例,当火电机组备用申报价格从真实成本逐渐降低,系统支付给火电机组的费用逐渐接近甚至低于火电机组发电成本,机组净利润降低甚至出现负值;当火电机组备用申报价格从真实成本逐渐升高,机组外部性价值减小,系统支付给机组的费用减少并趋于固定值,此时火电机组真实申报成本和虚假申报成本相同,表明该机组没有为新能源提供辅助服务,即机组未中标。
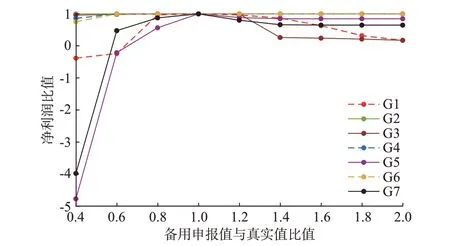
图4 发电机组不同备用申报系数下的净利润比值Fig.4 Ratio of net profits with different reserve bidding factors of generator units
可见,当火电机组申报的备用成本为真实成本时机组净利润最大,这表明VCG 机制满足激励相容性质,火电机组对其提供的辅助服务真实报价是最优报价策略。VCG 机制避免了市场成员的虚假报价行为,这有利于维持市场安全运行,提高市场经济效益。
4.1.3 基于最优基替换的加速算法
如前文所述,VCG 机制满足激励相容、个体理性、成本最小化等性质,在引入信息租金的分配机制后[12],VCG 机制不满足收支平衡的缺陷得到改进。但与边际价格机制相比,VCG 机制的计算效率仍需提升,为验证本文提出的基于最优基替换的加速算法的有效性,本节利用IEEE 57 节点系统,对比原始算法与基于最优基替换的加速算法在计算效率上的区别。
首先,对参与市场调度的发电机组进行优化出清,可得到各机组的最优出力和原问题的最优基,对原问题进行一次优化出清所用时间为0.155 7 s。
在得到原问题的最优基和机组最优出力后,辨识火电机组在VCG 机制下为市场成员提供的辅助服务价值。以火电机组8 为例,该机组的有功出力上限P8,G,max为550 MW,将 火电机组8 移 出 系统,即将P8,G,max设置为0,计算移除该火电机组后的系统成本,随后依据式(18)可最终得到该火电机组获得的系统支付。
在计算移除火电机组8 后的系统成本时,本文在原问题约束条件的右端项上添加Δb得到新问题,对机组8 而言,Δb=[0,…,0,-550,0,…,0]T。原问题的最优基即为新问题的初始可行基,依据前文具体步骤,得到移除机组8 后的各发电机组最优出力和新问题最优基。经计算,基于最优基替换的加速算法下新问题寻基所耗时间为0.068 1 s。而对新问题采用原始算法进行优化出清时,难以有效利用第1 次出清结果,此时新问题寻基所用时间明显变长,经计算,原始算法下新问题寻基所耗时间为0.143 3 s。对IEEE 57 节点系统移除发电机组i后优化寻基,并对寻基时间进行统计,在原始算法和基于最优基替换的加速算法下,移除各参与调度的火电机组后重新优化寻基的时间如图5 所示。
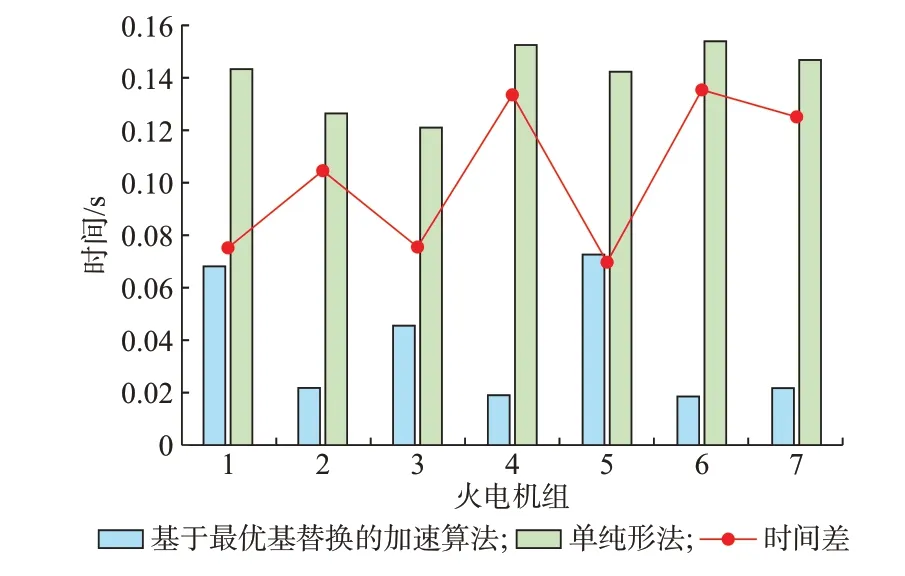
图5 IEEE 57 节点系统寻基时间对比Fig.5 Comparison of base-finding time of IEEE 57-bus system
其中,基于最优基替换的加速算法的平均寻基时间为0.038 2 s,而单纯形法的平均寻基时间为0.140 9 s,基于最优基替换的加速算法将计算效率提升了26.885%。从图5 可以看出,基于最优基替换的加速算法显著提高了VCG 机制的计算效率,这将为VCG 机制的广泛应用提供支持。
4.2 IEEE 118 节点系统
IEEE 118 节 点 系 统 包 含116 条 线 路、54 台 火 电机组,算例的相关参数及系统拓扑结构均参照IEEE 118 节点标准系统参数设置。IEEE 118 节点系统中共有19 台机组参与系统调度,剩余机组不参与调度且不为新能源并入电网提供辅助服务,因此,剩余35 台火电机组不在本文算例研究范围之内。
图6 给出了基于最优基替换的加速算法和单纯形法对于IEEE 118 节点系统的寻基时间,从图中可以看出,基于最优基替换的加速算法显著提高了VCG 机制的计算效率。本节统计了移除每台发电机组后的优化出清时间,其中,加速算法的平均优化出清时间为0.178 2 s;单纯形法的平均优化出清时间为1.429 0 s。在IEEE 118 节点系统中,加速算法将计算效率提高了69.792%。
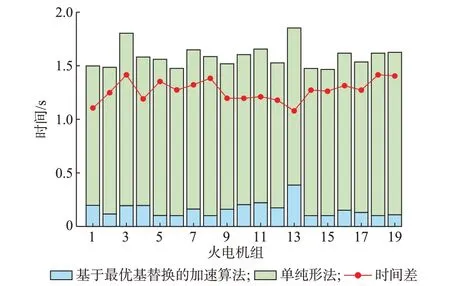
图6 IEEE 118 节点系统寻基时间对比Fig.6 Comparison of base-finding time of IEEE 118-bus system
5 结语
为促进主辅电力市场安全运行,提高市场经济效益,本文针对现有市场机制难以对市场成员外部性价值进行有效辨识的问题做进一步研究,量化市场成员外部性成本,提出主辅电力市场外部性价值优化定价方法。
与边际价格机制相比,VCG 机制需要逐台移除机组并重新优化出清,即对N台机组进行N+1 次优化出清,在计算效率上存在不足。为此,本文提出基于最优基替换的加速算法,在移除机组后将原问题的最优基重新选作新问题的初始可行基,利用对偶单纯形法在原问题最优基的基础上进行热启动,显著提高了VCG 机制的计算效率。最后,基于IEEE 57 节点系统和IEEE 118 节点系统算例验证基于最优基替换的加速算法的有效性。算例分析表明:1)基于VCG 的外部性价值分配机制满足占优策略的激励相容性质;2)对于IEEE 57 节点系统算例中添加的新能源机组,VCG 机制能够量化新能源机组并入电网的外部性成本,这将促进新能源参与交易;3)辨识火电机组为新能源及负荷提供的能量及辅助服务价值时,VCG 机制计算效率较低,针对该问题,本文提出基于最优基替换的加速算法,并验证了其在计算效率上的优越性。
未来,将在以下3 个方面继续探索:
1)本文利用基于最优基替换的加速算法提高了VCG 机制的计算效率,但在实际计算中仍需要分别移除每1 台发电机组进行重复优化出清。为了实现VCG 机制的广泛应用,避免重复优化的VCG 求解算法将是未来研究的重点。
2)考虑到中国自然资源分布和消费者低碳意识逐渐增强,更多有需求的用户将直接购买绿色电力,这将导致跨区域电力交易主体的决策行为发生改变。因此,随着电力系统中新能源的高比例渗入,各交易主体参与区域间电力交易的最优决策值得探讨。
3)本文研究以电力系统发电容量相对充足为前提,市场供需关系会对基于VCG 的外部性定价机制产生影响。因此,由于系统容量不足、供求关系紧张而导致的市场失灵问题值得进一步探讨。

