基于盖尔原理的逆变器并网系统稳定性判据
徐衍会,高天初,滕先浩,2
(1. 华北电力大学电气与电子工程学院,北京市 102206;2. 国网辽宁省电力有限公司大连供电公司,辽宁省大连市 116000)
0 引言
近年来,风电发展迅猛。风机通过电力电子逆变器接入电网,逆变器与电网的相互作用可能引发次同步振荡(subsynchronous oscillation,SSO),危及电网的安全稳定运行,该类振荡主要与电力电子换流器相关[1]。
阻抗分析法是分析逆变器并网系统稳定性问题的重要方法[2],它可以分析电力系统元件的阻抗-频率特性,具有明确的物理含义,适用于电力电子设备的谐波稳定性分析[3]。文献[4]将系统建模为源子系统和负载子系统,建立了逆变器的导纳模型,基于广义奈奎斯特稳定性判据(generalized Nyquist stability criterion,GNSC)分析了逆变器并网系统的稳定性。文献[5]提出了基于LCL 滤波电容电压全前馈的并网电流延迟级联反馈控制。文献[6]提出了一种自同步电压源逆变器(self-synchronous voltage-source inverter,SVI)改进控制策略,实现逆变器在不对称电网条件下的入网电流平衡输出,同时兼顾了SVI 对极端输出电压的稳定控制。文献[7]根据变换器的控制特性建立了电力电子变压器二次侧变换器及分布式能源逆变器的阻抗模型。文献[8]建立了锁相环、电流调节器等控制环节影响的阻抗分析模型,提出了多组逆变器并联接入弱电网的阻抗稳定性判据。文献[9]利用逆变器时间尺度自然分离的特性提出了一种基于时间常数的模型降阶方法。文献[10]提出一种基于阻抗测量的多逆变器系统稳定性校验方法,用于多个逆变器接入电网前的稳定性校验。以上研究基于阻抗分析方法分析了控制环节对系统稳定性的影响,但对于逆变器参数是否影响系统稳定性仍需要继续研究。
三相并网逆变器是一种多输入多输出系统,可以通过稳定性判据计算特征值来判定系统稳定性。当系统规模增大时,GNSC 这类方法需要逐点采样计算特征值,分析时间较长[11],不利于在线应用。
为了避免计算时间较长,通过矩阵元素估计特征值的分布范围来研究谐波谐振稳定域成为一种新的方向。在控制工程领域,文献[12-14]基于李雅普诺夫稳定理论和盖尔圆盘定理[15]提出了范数判据(norm criterion,NC),但是NC 保守性较高,判定结果准确率不高。文献[14]提出了D 通道判据和左半平面禁区判据(forbidden region-based criterion,FRBC)[16],D 通 道 判 据 在 实 际 应 用 中 有 较 大 局 限性,而FRBC 在分析车网系统的稳定性方面比其他判据要好,但是保守性仍然较高。文献[17]提出了一种基于阻抗模型和盖尔原理的并网逆变器稳定性判据。文献[18]基于盖尔原理提出一种构建参数稳定域的方法,降低了保守性。但是这些应用于多输入多输出系统的简化稳定性判据依旧有较高局限性。
本文基于盖尔原理提出了快速低保守性稳定性判 据(fast low-conservativeness stability criterion,FLCSC)。FLCSC 可以对系统特征值所在范围进行快速估计而非具体的特征值计算,能够提升稳定域构建效率。通过建立直驱风电场并网模型,对比分析不同稳定性判据的计算速度和准确性,验证了FLCSC 的计算速度较快,虽然稳定性判断依然具有保守性,但FLCSC 的保守性大大降低。
1 逆变器并网系统及等效电路
1.1 系统结构
新能源逆变器并网系统结构如图1 所示,逆变电路输出电流经滤波和升压后接入主电网,电流内环的反馈信号为逆变侧电感电流,锁相环的输入电压为变压器低压侧电压。
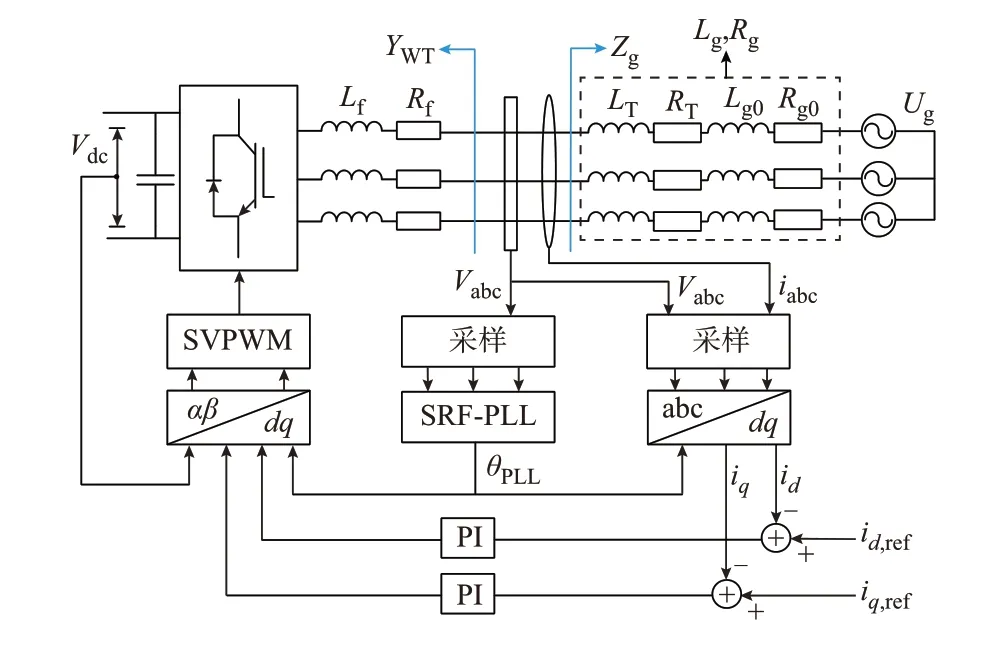
图1 逆变器并网系统结构Fig.1 Structure of grid-connected inverter system
图1 中:Vdc为直流侧母线电压幅值;Vabc为网侧母线三相电压幅值;iabc为网侧三相电流;id和iq分别为网侧电流的d、q轴分量;id,ref和iq,ref分别为d、q轴电流给定值分量;θPLL为由同步坐标系锁相环(synchronous reference frame phase-locked loop,SRF-PLL)得到的电网电压相位信息;PI 表示比例-积分控制器;Lf和Rf分别为逆变侧电感、电阻;Ug为网侧电源电压;SVPWM 表示空间矢量脉宽调制。为便于阻抗建模与稳定性分析,将变压器阻抗和电网阻抗折算到低压侧,根据变压器电感LT、电阻RT和电网阻抗电感Lg0、电阻Rg0可得电网侧电感Lg、电阻Rg,阻抗建模时可将图1 中滤波电感右侧视为公共连接点(point of common coupling,PCC),由PCC向逆变器看可得逆变侧导纳YWT,由PCC 向电网看可得电网侧阻抗Zg。
1.2 逆变器并网系统等效电路
由于并网逆变器的稳态轨迹呈周期性变化,系统没有固定的直流工作点,不能用传统的小信号线性化方法建模。为此,提出了dq轴线性化建模方法[18],将交流逆变器模型转换到dq轴坐标系。不同于阻抗分析法,dq轴线性化建模是将三相并网逆变器等效为2 个相互耦合的直流系统,从而推导出dq轴阻抗模型。
假设矩阵UPCC(s)为PCC 电压,Ig(s)为并网电流,三相并网逆变器等效为理想电流源矩阵Ieq(s)和输出导纳矩阵YWT(s)并联。在分析逆变器并网系统稳定性时,任意频率s下电流Ig(s)的表达式为:
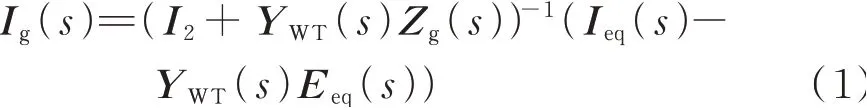
式中;I2为2×2 的单位矩阵;Zg(s)为电网阻抗矩阵;Eeq(s)为电网等效电源的电势。
当电流源和电压源均保持恒定时,风电场和电网在各自单独运行时才能够保持稳定。因此,逆变器并网系统稳定的条件是当且仅当逆变器输出导纳与电网阻抗乘积YWT(s)Zg(s)满足GNSC。
2 GNSC
GNSC 定义:使多变量反馈系统处于开环不可控模式,其相应的特征频率处于右半平面内,当且仅当回率矩阵L(s)=G(s)K(s)的特征值集对临界点(-1,j0)的逆时针包围净和等于前向通道传递函数G(s)和反馈通道传递函数K(s)的右半平面极点的总数,该系统是闭环稳定的[19]。根据GNSC,当且仅当回率矩阵L(s)的2 个特征值λ1(s)和λ2(s)在任意频率s下围绕临界点(-1,j0)逆时针包围的净和等于风电场导纳矩阵YWT(s)和电网阻抗矩阵Zg(s)的右半平面极数总和时,系统闭环稳定。
回率矩阵L(s)为:
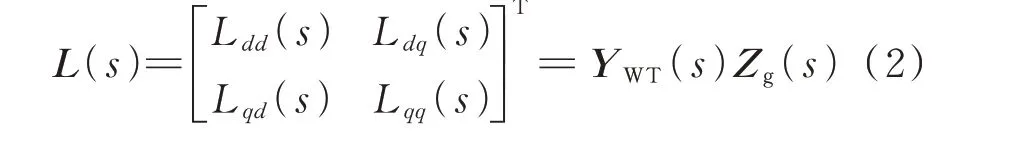
式 中:Ldd(s)、Ldq(s)、Lqd(s)、Lqq(s) 为 回 率 矩 阵L(s)的元素。
3 基于盖尔原理的稳定性判据
3.1 盖尔原理
为了简化稳定性分析,回率矩阵L(s)的特征值可以用盖尔原理来估计:A为一个n×n矩阵,ai,j为

相似矩阵定理3:若n阶矩阵A与B相似,则A与B的特征多项式相同,从而A与B的特征值亦相同[20]。可以通过使用2 个具有相同特征值的回率矩阵来提高特征值估计的准确性,即回率矩阵L(s)和L2(s)。
因此,特征值λ1(s)和λ2(s)会位于根据2 个回率矩阵L(s)和L2(s)所得到的盖尔圆盘的相交部分,可通过利用2 个特征值相同但是形式不同的系统回率矩阵来提高对特征值位置估计的准确性。
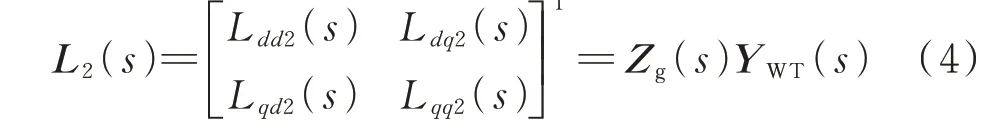
式 中:Ldd2(s)、Ldq2(s)、Lqd2(s)、Lqq2(s)为 回 率 矩 阵L2(s)的元素。
如图2 所示,分别以回率矩阵L(s)、L2(s)对角线元素为圆心,非对角线元素幅值为半径,不同频率下在复平面上形成蓝色、黑色圆带。
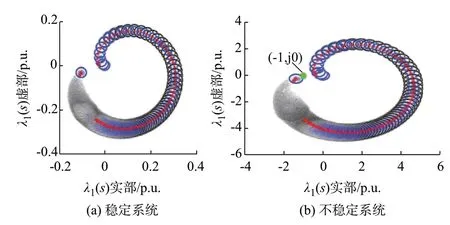
图2 回率矩阵的圆带轨迹示意图Fig.2 Schematic diagram of circular belt trajectory of return ratio matrix
图2 中,红色轨迹为特征值轨迹,即广义奈奎斯特曲线。根据GNSC,当圆带逆时针包围(-1,j0)的极数净和与风电场导纳矩阵YWT(s)和电网阻抗矩阵Zg(s)的右半平面极数总和相等时,系统稳定;反之,系统不稳定。
3.2 FLCSC
若状态矩阵元素为关于控制参数的函数,则可根据圆盘定理结合李雅普诺夫稳定条件获得参数的稳定边界,即得到相应的参数稳定域[18]。
只要λ1(s)和λ2(s)在任意频率s下的特征根轨迹不进入不稳定区,就可以保证特征根轨迹不穿越-1 的左实轴,从而不包围临界点(-1,j0)。
根据GNSC,回率矩阵L(s)的特征轨迹越接近临界点,系统的稳定性裕度越低。因此,测量从临界点到盖尔圆盘上最接近点的距离作为系统的稳定性裕度ΔsΙ:

交点的位置用于判断系统的稳定性。若横坐标交点的值小于或等于-1,则系统不稳定;否则,系统稳定。
基于回率矩阵L(s)的2 个稳定条件QFLCSC1和QFLCSC2在任意频率下均为正。由于回率矩阵L(s)和L2(s)的特征值相同,因此,回率矩阵L(s)的所有特征值也分布在回率矩阵L2(s)的盖尔圆盘中。盖尔圆盘与实轴交点的位置ΔxΙ可表示为:
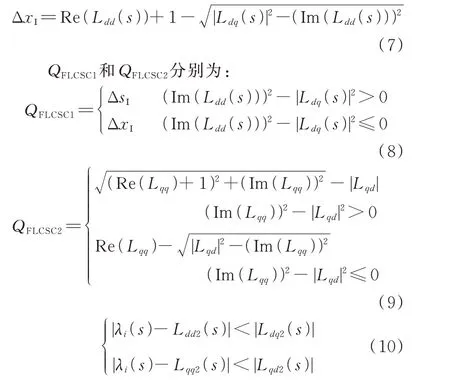
基于回率矩阵L2(s)的2 个稳定条件QFLCSC3和QFLCSC4分别如式(11)和式(12)所示。
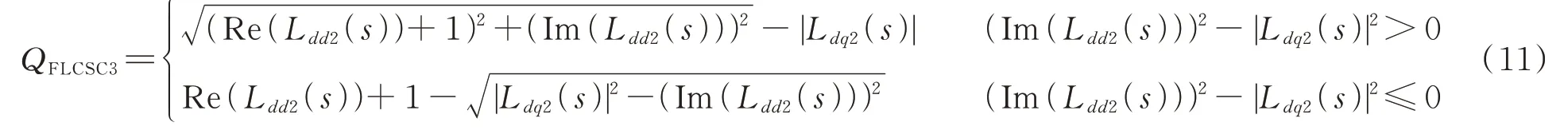
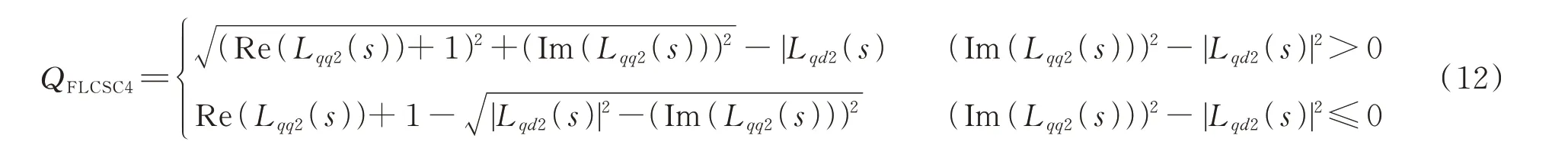
所有特征值都位于回率矩阵L(s)与L2(s)的盖尔圆盘的相交处。设2 个事件a 和b 分别表示回率矩阵L(s)和L2(s)的盖尔圆盘在稳定区,即肯定域。aˉ和bˉ分别为事件a 和b 的相反事件。稳定系统的否定域可以减小为aˉ和bˉ的交集。
稳定系统的肯定域为事件a 和b 的并集。事件a 满足式(13),事件b 满足式(14),因此,肯定域应满足式(13)或式(14),即FLCSC 稳定系统的条件。
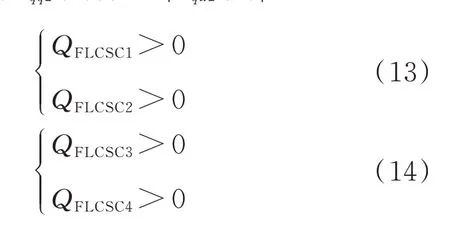
图3(a)和(b)分别为NC 和FRBC 的稳定域示意图。与FRBC 相比,FLCSC 的不稳定区进一步减小到-1 的左实轴上,如图3(c)所示。
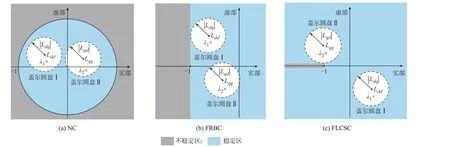
图3 3 种稳定性判据下回率矩阵L(s)特征值的禁区范围Fig.3 Forbidden region of eigenvalues for return ratio L(s)with three stability criteria
4 直驱风电场并网系统稳定性算例
算例采用如图4 所示的等值系统模型:大型风电场包括800 台参数相同的直驱风机,单机容量为1.5 MW,经过单台逆变器、机端箱式变压器(0.69 kV/35 kV)升压后汇集到汇流站母线,经变压器升压后接入交流主网。T1、T2、T3分别为35 kV/110 kV、110 kV/220 kV、220 kV/750 kV 等级的升压变压器,Z110和Z220分别为110 kV 线路与220 kV 线路的等效阻抗。直驱风机详细参数见附录A 表A1。
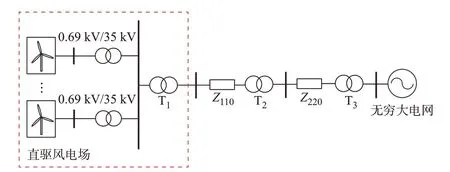
图4 直驱风电场并网系统示意图Fig.4 Schematic diagram of grid-connected system of direct-drive wind farm
直驱风机并网逆变器采用SRF-PLL[19],相应的开环传递函数HPLL(s)为:
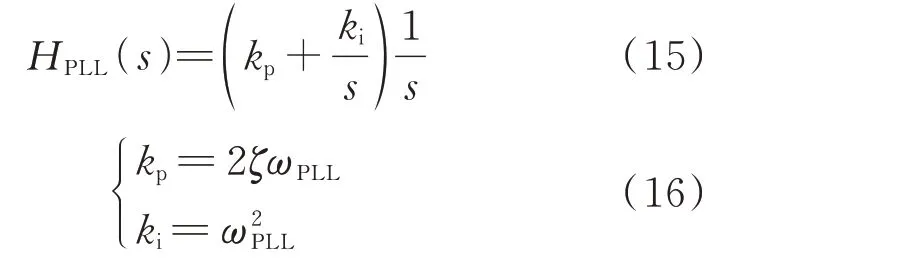
式中:kp和ki分别为锁相环的比例、积分系数;ζ=1/ 2 为最佳阻尼特性;ωPLL为自然频率。ωPLL越大,调整时间越短,响应速度越快,但较大的ωPLL会影响滤波能力。
4.1 不同判据的稳定性分析结果
应用不同稳定性判据对算例系统稳定性进行分析。图5 中:2 个NC(即NC1 和NC2)判断系统不稳定;4 个FRBC(即FRBC1 至FRBC4)判断系统不稳定;4 个FLCSC(即FLCSC1 至FLCSC4)判断系统稳定;GNSC 判断系统稳定。可以看出,本文提出的FLCSC 与GNSC 的结果一致,准确性高于NC 和FRBC。
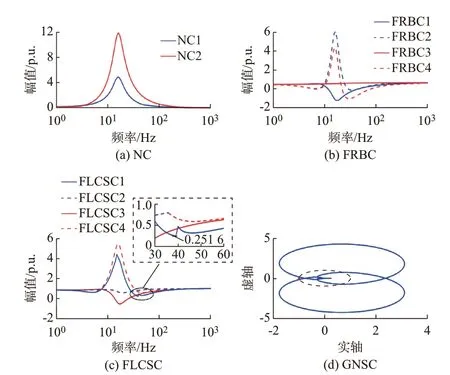
图5 不同判据的稳定性分析Fig.5 Stability analysis of different criteria
4.2 不同判据的稳定域保守性对比分析
本节构建以锁相环角频率和电网电抗值为参数的稳定域,分析不同判据的保守性。首先,调整系统连接电抗Xg和ωPLL,固定其他参数以获得不同的工况。对于每种工况,系统的稳定性均由GNSC、FLCSC、FRBC、NC 进 行 评 估,其 稳 定 域 如 图6所示。
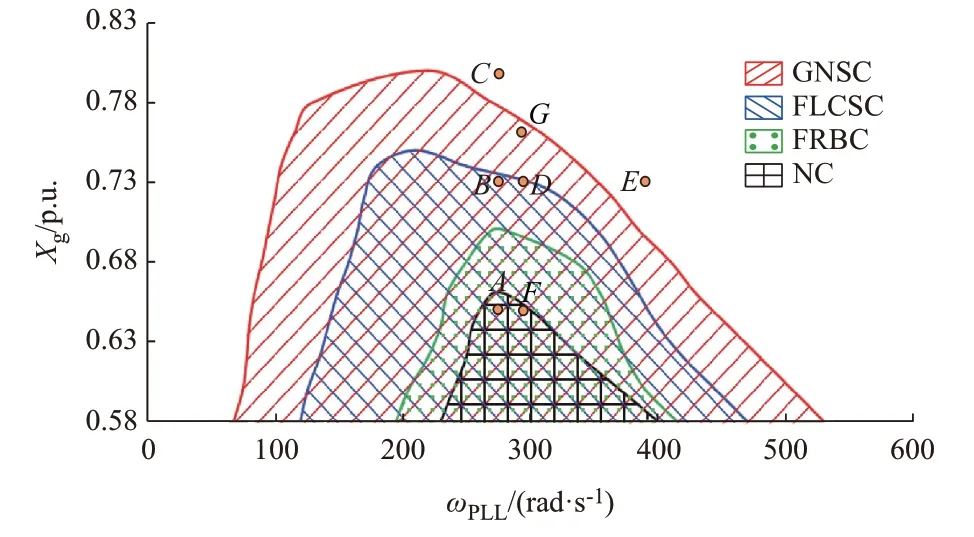
图6 不同判据的稳定域Fig.6 Stability regions of different criteria
图6 中阴影部分表示稳定域。可以看出NC 和FRBC 的稳定域过于保守,可能会出现系统稳定而被误判为不稳定的情况,判据准确性较低;本文提出的FLCSC 比NC 和FRBC 的稳定域更大,保守性大大降低,从而提高了稳定性判断的准确性。
4.3 时域仿真验证
为了验证所提FLCSC 的有效性,在PSCAD/EMTDC 中搭建了如图4 所示直驱风电场并网系统仿真模型,仿真结果如图7 所示。
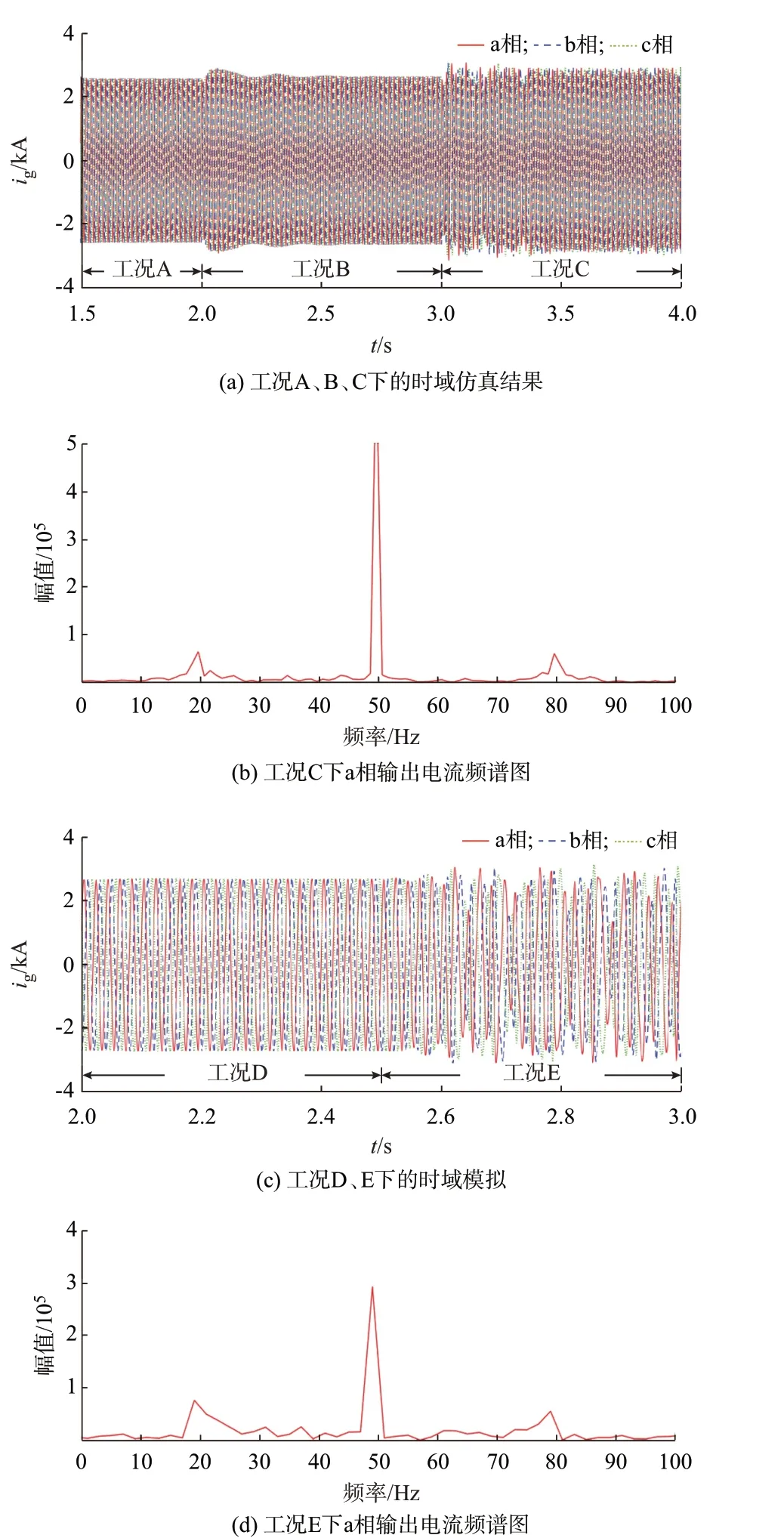
图7 时域仿真结果Fig.7 Results of time-domain simulation
2 s 时,由工况A 变为工况B,风电场出口电流ig最终稳定。3 s 时,由工况B 变为工况C,ig开始振荡,与FLCSC 的分析结果一致。2.5 s 时,由工况D变为工况E,ig开始振荡,频谱图如图7(d)所示。可见,时域仿真结果验证了本文所提FLCSC 的有效性。
4.4 不同稳定性判据的计算时间对比
4 种判据稳定性分析与仿真结果比较如表1 所示。可以看出,FLCSC 与GNSC 的结果在所有情况下一致。FLCSC 比NC 和FRBC 的稳定性分析更准确,且保守性更低。
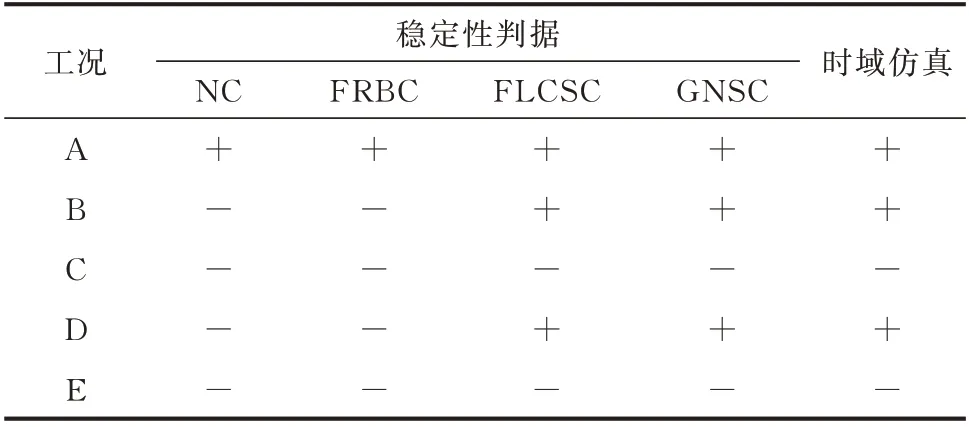
表1 典型工况的稳定性分析Table 1 Stability analysis of typical working conditions
表2 显示了每次判据的程序运行时间。由于GNSC 需要连续求解矩阵的特征值,所以运行时间较长,而FLCSC 计算速度比GNSC 快很多。计算机处理器为2.60 GHz Intel Core i5-6440HQ。
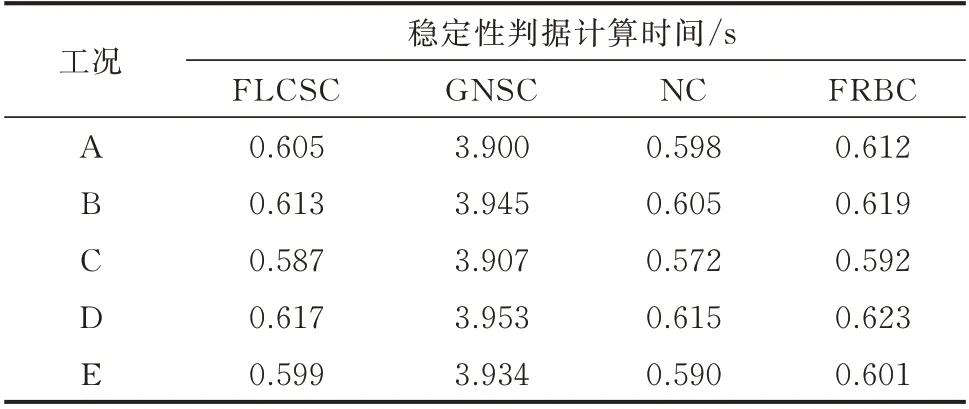
表2 稳定性判据的计算时间Table 2 Computation time of stability criteria
与GNSC 相比,FLCSC 仍然具有保守性,本文也给出这种情况下FLCSC 的判定结果和仿真验证。调整锁相环频率和电网电抗,使系统从F点运行至G点,此时仍在GNSC 的稳定域内而在FLCSC的稳定域外。GNSC 和FLCSC 的结果和时域仿真曲线如图8 和附录A 图A1 所示。
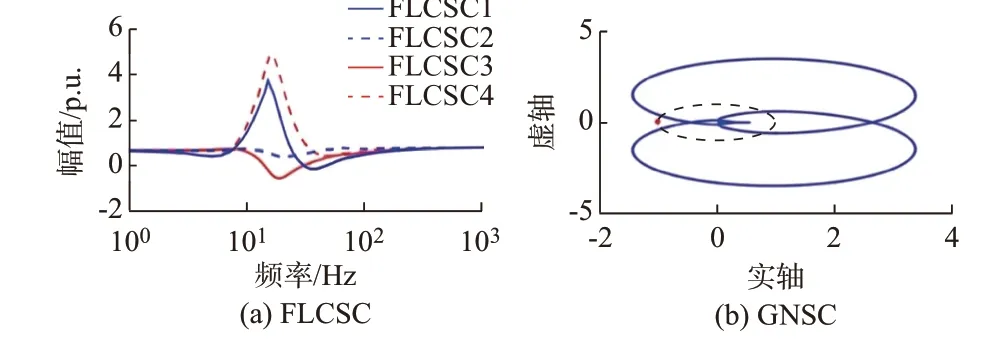
图8 FLCSC 与GNSC 的稳定性分析Fig.8 Stability analysis of FLCSC and GNSC
可以看出,FLCSC 判断系统运行在G点不稳定,而GNSC 判断该运行点系统稳定。时域仿真结果表明,系统从F点切换至G点并未发生次同步振荡,系统稳定。
5 结语
本文在盖尔原理的基础上,缩小禁区范围并根据概率论原理推导了用于判断逆变器并网系统稳定性的FLCSC,通过与现有判据的对比分析和时域仿真验证得出以下结论:
1)与GNSC 相比,FLCSC 不需要逐点采样计算特征值,计算速度更快;
2)与NC 和FRBC 相比,FLCSC 保守性更低,从而显著提升了稳定性判断的准确度。
FLCSC 作为一个实用的系统稳定临界点估算方法,在系统参数不断变化时能避免耗时较长的逐点计算,快速估算出系统的稳定区域。
本文构建稳定域是以锁相环角频率和系统电抗为参数的,除此之外其他参数也可能较大程度地影响稳定域。选择2 个参数构建的是二维稳定域,选择3 个参数构建的可能是三维乃至多维稳定域。后续将研究影响稳定域的参数,力求得到更准确的稳定域,提高稳定性判据的准确性。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

