基于截断系数实现状态合并的直流配电系统可靠性评估

高清旭，梁定康，韩肖清，王 磊

（太原理工大学电气与动力工程学院，山西省太原市 030024）

0 引言

相较于交流配电系统，直流配电系统具有供电容量大、电能质量高、便于新能源接入等优点［1-2］。直流配电系统可靠性评估是保证用户安全可靠用电的重要环节之一。目前，直流配电系统的工程应用较少［3］，可靠性的研究相对匮乏，现有研究主要集中在以下3 个方面：

1）直流设备建模。系统可靠性水平取决于系统中各类设备的可靠性水平。直流配电系统包含大量电力电子设备（直流断路器、直流变压器等），评估直流配电系统的可靠性需要建立直流设备的故障模型［4-5］。文献［6］采用部件计数法建立了电压源型换流器、直流变压器和直流断路器的可靠性模型，分析了器件级冗余和设备级冗余对直流配电系统可靠性的影响。 文献［7］基于模块化多电平换流器（modular multilevel converter，MMC）的组件串并联关系和冗余配置建立了可靠性模型，采用最小割集法评估直流配电系统可靠性。

2）直流配电系统故障后果分析。电力系统中，某些设备发生故障可能导致负荷停电，需要根据负荷停电情况计算系统可靠性指标。因此，故障后果分析是评估直流配电系统可靠性的重要环节之一。文献［8］在最小割集法的基础上，考虑直流负荷比例系数、分布式电源供电路径等因素的影响，并将改进后的最小割集法应用于直流配电系统可靠性评估。文献［9］结合直流变压器、直流断路器等直流设备的马尔可夫模型改进最小路法，分析了孤岛内有无分布式电源接入对直流配电系统可靠性的影响。

3）直流配电系统状态选取。在直流配电系统中，随着功率半导体器件的发展与应用［10］，直流电源能够根据负荷需求灵活调节输出功率［11-12］，拥有多个输出层级。直流配电系统存在真双极、伪双极等多种接线方式［13-15］，负荷既可以单极运行，也可以双极运行，运行方式灵活多变。电源输出层级与负荷运行方式之间存在多种组合形式，进一步增加了直流配电系统的运行状态［16］。因此，状态合并对直流配电系统更有意义。传统的状态合并方法［17］以转移率（设备故障率和修复率）相同为合并前提，但在电力系统实际运行中，即便是同一工况下的相同设备，故障率和修复率也存在差异，无法在直流配电系统中实现大规模应用，导致多状态直流配电系统的可靠性评估效率低下。

本文提出基于故障树分析法［18-19］和马尔可夫过程［20-22］的状态合并方法，通过引入截断系数C提高合并状态转移率的求解效率，实现了差异化转移率情况下的状态合并，以改进的IEEE-RBTS BUS 6直流配电系统为例验证了所提方法的有效性。

1 直流配电系统多状态分析与建模

直流配电系统往往存在多个直流电源和多种负荷运行方式，本章以如图1 所示的真双极系统为例，分析直流配电系统的多种运行状态。中压侧电压等级依据文献［9］以及中国江苏省苏州工业园区的中压直流示范工程［2］设定为±7.5 kV，低压侧电压等级设定为±375 V。

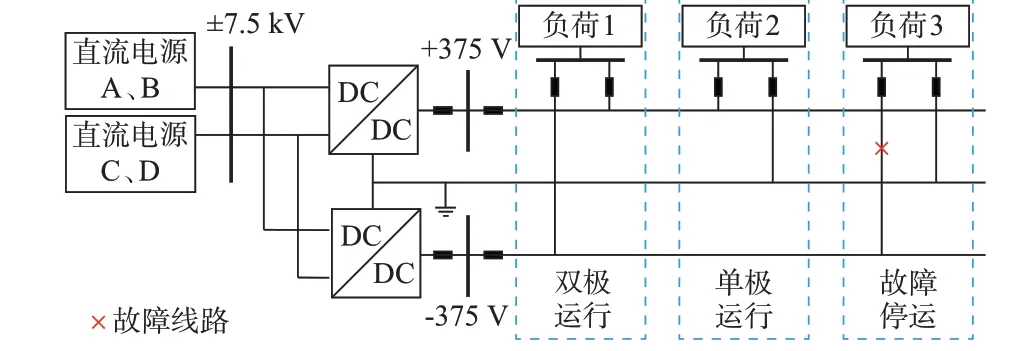
图1 直流配电系统源-荷运行状态Fig.1 Source-load operation state of DC distribution system

由图1 可知，直流配电系统共有4 个直流电源，每个电源都有“工作”和“故障”2 种状态，4 个电源共有24=16 种状态，分别对应双极运行、3/4 双极运行、1/2 双极运行、单极运行、1/2 单极运行以及故障停运，上述系统运行状态之间的转移关系通过转移率（设备故障率和修复率）描述。马尔可夫过程是分析可修复系统状态转移过程的常用方法。本章选用马尔可夫过程建立直流配电系统的状态空间模型如图2 所示。图中：i1至i16为系统状态编号；γ1至γ4、μ1至μ4分别为4 个直流电源的故障率和修复率。

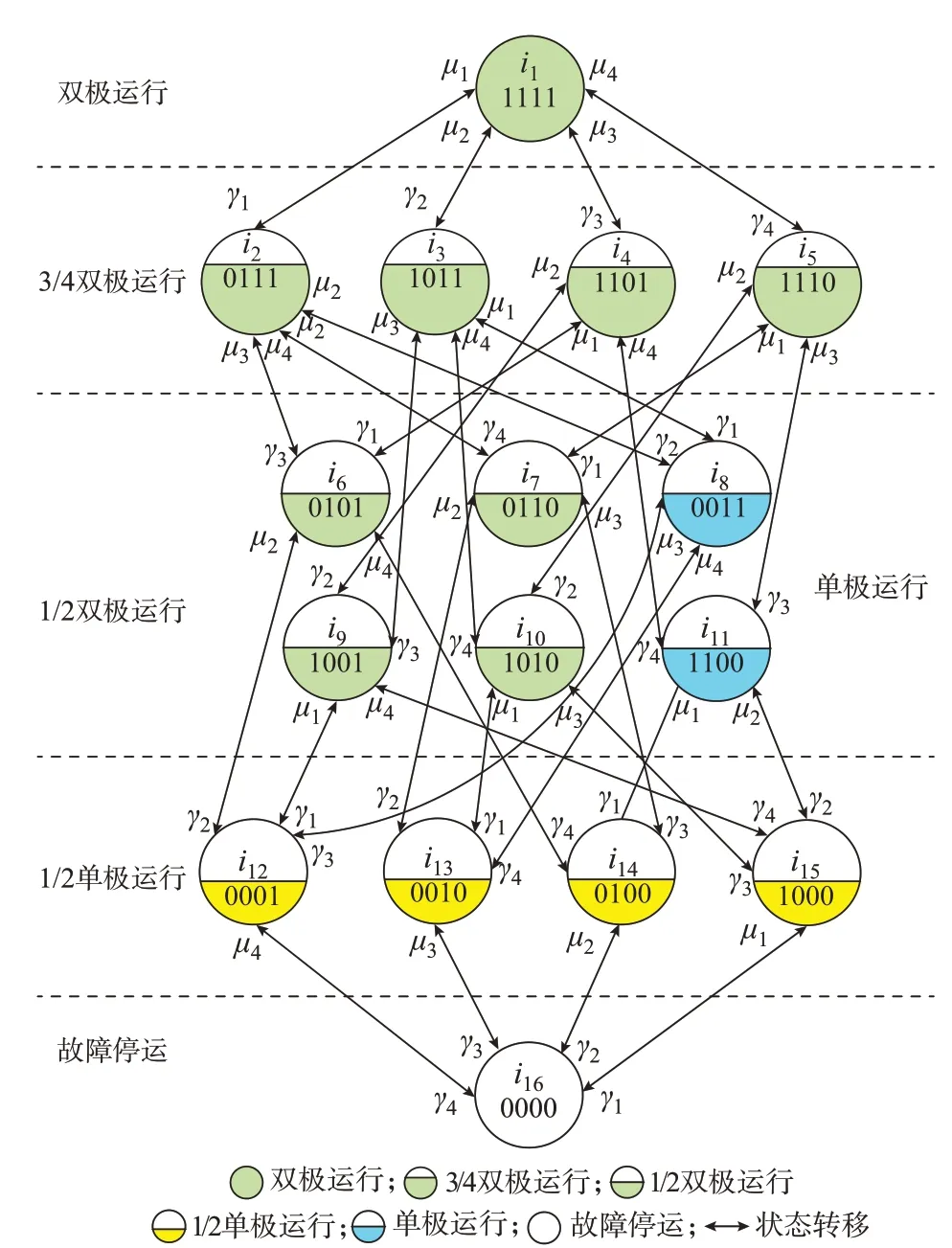
图2 直流配电系统状态空间模型Fig.2 State space model of DC distribution system

在确定直流配电系统状态空间模型的基础上，求解状态概率是本章的主要研究内容。首先，根据直流配电系统状态空间模型建立转移矩阵A，表达式为：

式中：Ai，j为矩阵A的元素，i、j为系统状态编号，当i≠j时，Ai，j数 值 上 为 状 态i到j的 转 移 率，当i=j时，Ai，j数值上等于1 减去该行非对角线元素之和。

根据马尔可夫过程可知，当系统达到稳态运行时，状态概率不随系统运行状态的改变而改变［19］，表达式为：

式中：P=[p1，p2，…，p16]为系统状态概率行向量。

式（2）可等效为：

式中：I为单位矩阵。

通过式（3）的转置运算，得到矩阵代数方程为：

由于矩阵(A-I)T的对角线元素可由非对角线元素表示，因此不是满秩矩阵，无法求解系统状态概率，于是增加“系统所有状态概率之和为1”的全概率条件，表达式为：

式中：pi为系统处于状态i的概率。

联立式（4）和式（5）可得系统状态概率为：

2 状态合并

2.1 状态合并的条件分析

传统状态合并方法基于相同的状态转移率确定待合并的系统运行状态［17］。在电力系统实际运行中，几乎不存在转移率相同的应用场景。但在相同或相似的场景中，可能存在设备故障率、修复率相近的情况。因此，本节提出了基于差额阈值δ的状态合并条件，差额阈值的选取依据工程实际需求及可靠性评估精度。在计算状态转移率与参考值差值的基础上，将差值绝对值小于或等于差额阈值的系统运行状态确定为待合并状态，表达式为：

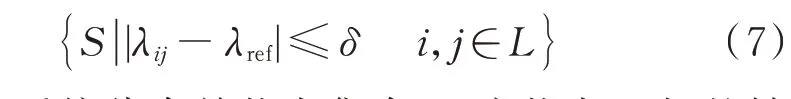
式中：S为系统待合并状态集合；λij为状态i到j的转移率，如果状态i为故障状态，则λij为修复率，反之为故障率；λref为转移率参考值；L为系统状态集合。

需要注意的是，给出的状态合并条件虽然在数学方法上实现了相近系统运行状态的聚类，但为了体现可靠性评估的合理性，一般基于同类设备选择待合并的系统运行状态。在实际工程应用中，异类设备的状态合并缺乏合理性与可解释性。

2.2 合并状态转移率的求解

合并状态转移率定义为合并状态与待转移状态之间的转移率，包括故障率或修复率。以图2 中3/4双极运行方式为例，假定该运行方式的4 个状态合并为一个状态（合并状态），需要确定该合并状态与双极运行的独立状态（待转移状态）之间的转移率。由此可推知，合并状态转移率包括2 种形式：合并状态与独立状态之间的转移率；合并状态之间的转移率。本节针对上述2 种形式开展转移率的求解分析。

2.2.1 合并状态与独立状态之间的转移

本节阐述合并状态与独立状态之间的转移率求解方法。如图3（a）所示，拟定系统的4 个状态合并为状态J，求解合并状态与独立状态i之间的转移率。虽然解析过程以4 个状态合并为例，但所提方法可推广至多状态合并与独立状态之间的转移率求解。

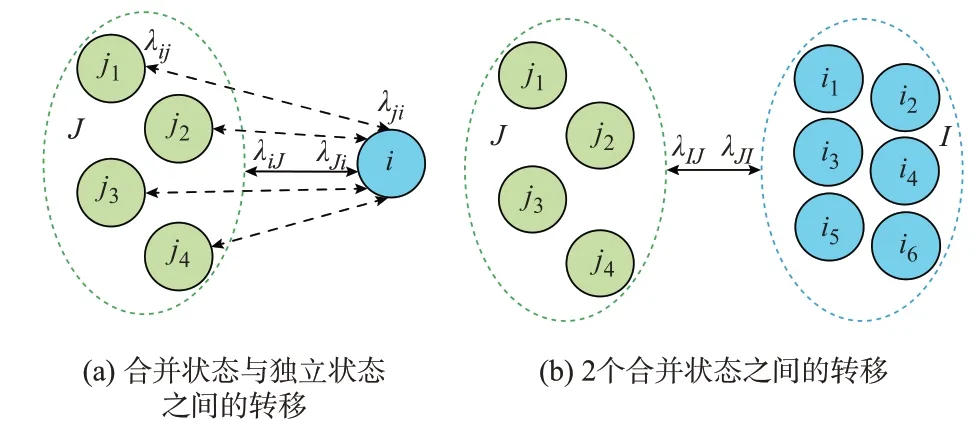
图3 合并状态之间的转移Fig.3 Transition between merged states

由图3（a）可知，状态i到状态J的转移频率有2 种描述方式：1）状态J作为合并状态，状态i到状态J的转移频率等于状态i的概率乘以状态i到状态J的转移率［17］；2）状态J拆分为4 个独立状态，状态i到状态J的转移频率等于状态i到每个独立状态j的转移频率求和。由于图3（a）所示为遍历系统，2 种方式下的转移频率在数值上相等，表达式为：

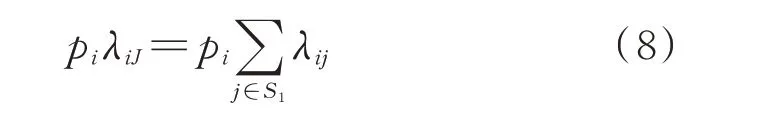
式中：S1为状态J中的待合并状态集合。

消去公因子pi，得到状态i到状态J的转移率λiJ为：

上述过程求解了状态i到状态J的转移率，为了满足可靠性评估要求，以下部分介绍状态J到状态i的转移率求解方法。与式（8）的分析过程类似，状态J到状态i的转移概率为：

式中：pJ为系统处于合并状态J的概率。

由式（10）可知，转移率λJi的求解分为2 种情况。第1 种情况，当状态转移率λji相同时，即传统状态合并方法，不需要求解系统状态概率，根据式（10）求得状态J到i的转移率λJi为：

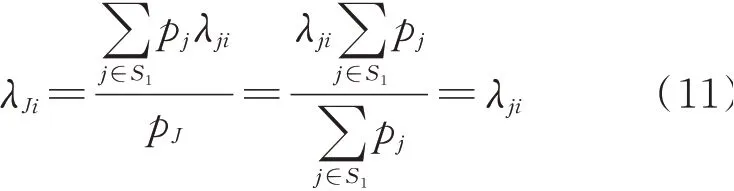
第2 种情况，当状态转移率λji不同时，求解转移率λJi需要计算系统状态概率。虽然状态概率可以通过马尔可夫过程求解，见式（1）至式（6），但由于直流配电系统运行状态较多，若采用马尔可夫过程求解，消耗的时间将大于状态合并所节省的时间。为提高状态转移率的求解效率，本文提出基于截断系数C的转移率求解方法。令C=pj/pk，代入式（10）约去公因子pk，得到状态J到状态i的转移率λJi如式（12）所示。由此可见，当转移率不同时，截断系数C的求解是状态合并的关键，截断系数的分析及计算过程详见2.3 节。

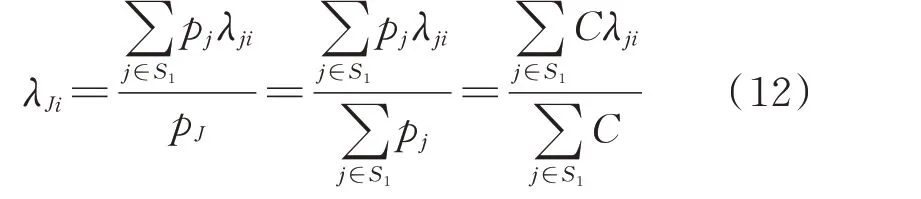
2.2.2 2 个合并状态之间的转移

本节主要阐述将多个系统运行状态合并后，如何求解2 个合并状态之间的转移率。以图2 中的1/2 双极运行、单极运行为例，将2 种运行方式包含的6 个状态合并后，为开展可靠性评估，需要确定该合并状态I与上一层合并状态（3/4 双极运行的合并状态J）之间的转移率。根据上述分析建立状态合并模型如图3（b）所示。图3 中，状态转移率λIJ和λJI的求解过程如下。

根据遍历系统的频率概念可知，状态I到J的转移频率为：

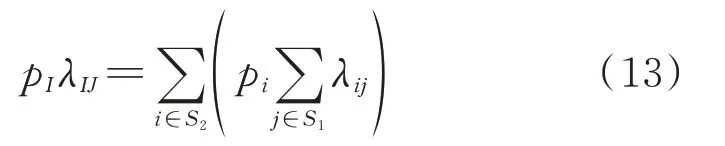
式中：S2为合并状态I中的待合并状态集合。

分析式（13）可知，转移率λIJ的求解分为2 种情况。第1 种情况，当状态转移率λij相同时，合并状态转移率λIJ为：

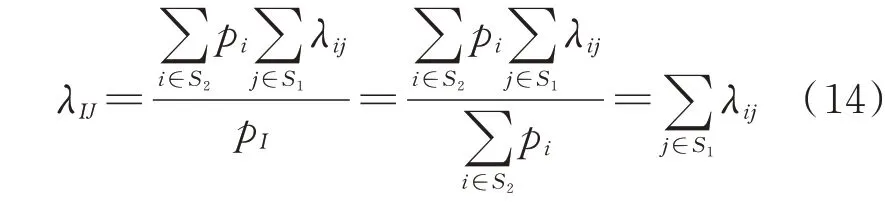
第2 种情况，当状态转移率λij不同时，合并状态转移率λIJ为：

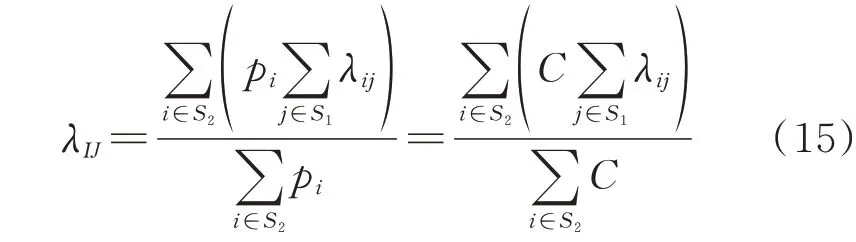
状态J到状态I的转移率求解过程与状态I到状态J的转移率求解过程类似，为避免冗余，当状态转移率λji相同或不同时，合并状态转移率λJI的求解过程分别如式（16）和式（17）所示。

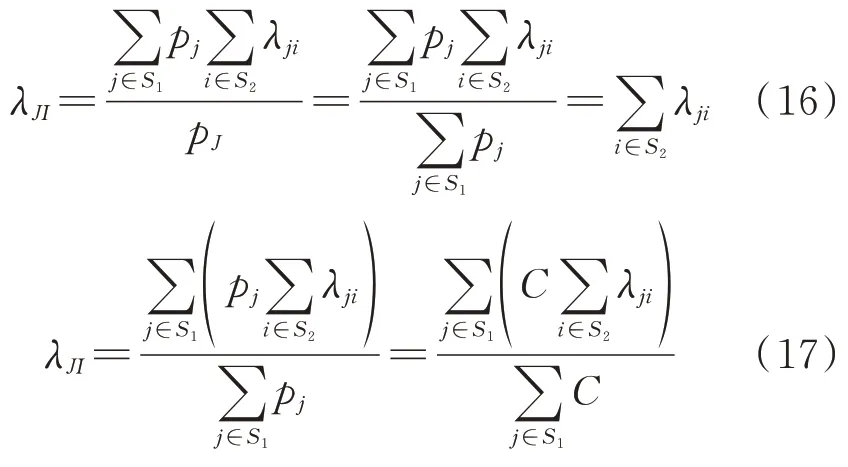
状态合并部分主要介绍了状态合并条件与合并状态转移率的求解方法，二者结合可用于简化直流配电系统状态空间模型（见图2）。首先，根据状态合并条件确定模型每一层的待合并状态；其次，根据转移率求解方法建立合并状态之间的转移关系。状态空间模型的简化有利于提高直流配电系统可靠性评估效率。

2.3 截断系数的求解方法

为提高合并状态转移率的求解效率，实现差异化转移率情况下的状态合并，本节研究了截断系数C的求解方法。首先，该方法根据故障树分析法确定截断系数随时间变化的截断函数C(t)。其次，利用马尔可夫过程确定截断函数达到稳态时段tp。最后，将稳态时间代入截断函数从而确定截断系数C=C(tp)。

2.3.1 截断函数的求解过程

在故障树分析法中，系统运行状态的概率取决于系统各设备所处状态的概率［18］，设备的可用率通过可靠度函数R(t)描述。当设备工作于稳态阶段时，其故障率为常数γ，此时，可靠度函数R(t)=e-γt表示设备在（0，t）区间内处于工作状态的概率［17］。根据故障树分析法，直流配电系统状态概率函数等于系统部分设备处于工作状态的概率乘以剩余设备处于故障状态的概率，具体表达式为：

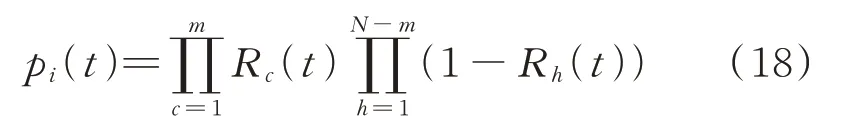
式中：pi(t)为时段t状态i的概率函数；Rc(t)和Rh(t)分别为时段t第c个和第h个设备的可靠度函数；m为状态i中正常运行的设备数量；N为系统设备总数。

截断函数C（t）描述了截断系数C随时间的变化规律。由2.2.1 节可知，C=pj/pk，其中，状态j为待合并状态，状态k为参考状态，参考状态可在待合并状态中任意选取。由式（18）可知，只要确定pi(t)的稳态值即可求得合并状态I中每一个独立状态i的概率。根据截断系数的定义可知，截断函数的表达式为：

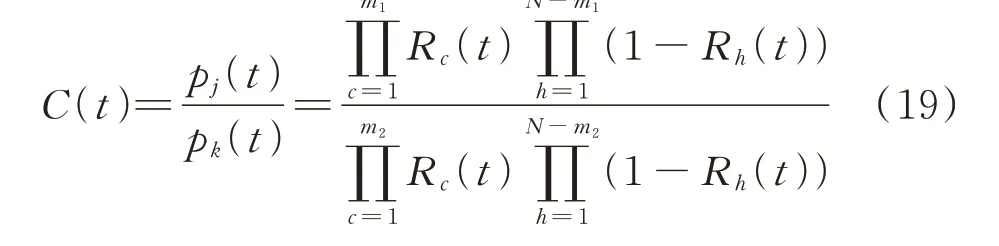
式中：m1和m2分别为独立状态j和状态k中正常运行的设备数量。

需要注意的是，故障树分析法求解状态概率的效率高于马尔可夫过程；截断函数的比值运算约去了2 个状态概率函数的公因式，进一步提升了求解效率。

2.3.2 稳态时间tp的求解过程

系统达到稳态运行的时段t即为稳态时间tp，本节利用马尔可夫过程求解系统达到稳态的时间。首先，根据马尔可夫过程得到一组关于系统状态概率函数的微分方程为［17］：

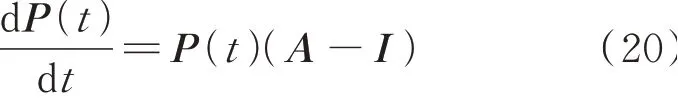
式 中：P(t)=[p1(t)，p2(t)，…，pi(t)，…]T为 状 态概率函数列向量。

其次，对式（20）应用拉氏变换，变换过程为：

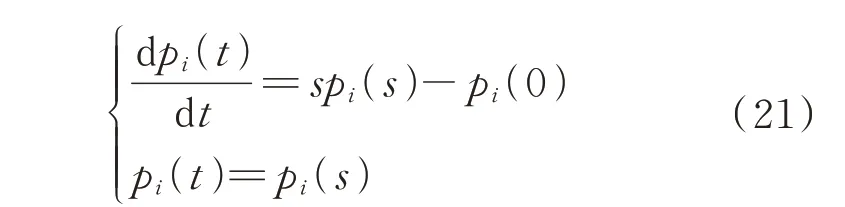
对于多状态直流配电系统，一般设状态p1为正常工作状态。任意设备在投入运行时必然处于正常工作状态，因此有p1(0)=1，p2(0)=p3(0)=…=pi(0) =…=0。结合上述条件将式（21）代入式（20）得到P(s)=[p1(s)，p2(s)，…，pi(s)，…]T的表达式为：

对式（22）应用反拉氏变换得到系统状态概率的函数曲线如图4 所示。

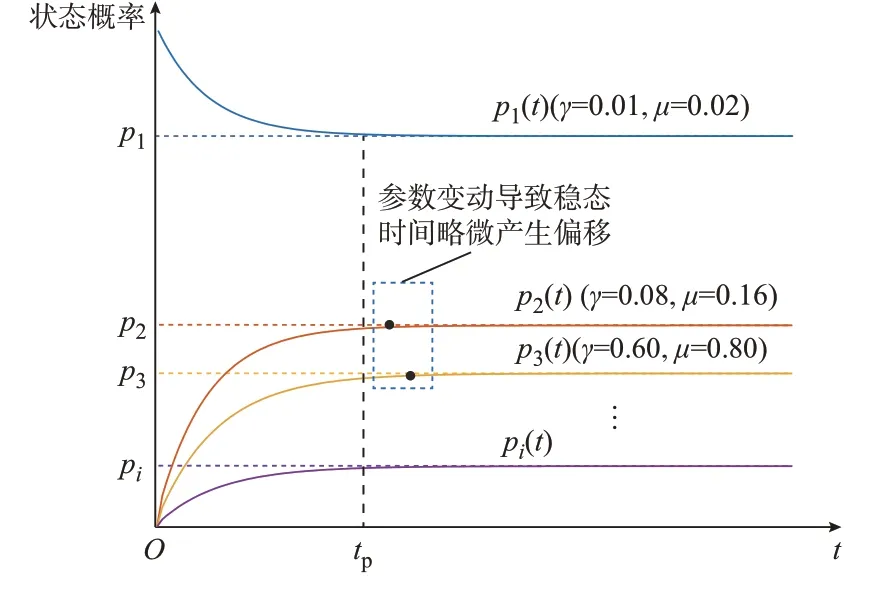
图4 状态概率函数曲线Fig.4 Curve of state probability function

由图4 可知，系统状态概率函数为单调函数，且收敛速度很快。当状态概率函数pi(t)与pi(t+Δt)差值的绝对值首次小于ε时，认为系统达到稳态运行，其中，ε为无穷小量。此时，自变量t即为稳态时段tp，表达式为：

2.3.3 截断系数的求解过程

马尔可夫过程与故障树分析法都是由指数函数衍生的，因此具有相同的函数主体。由于二者在数学本体上存在联系，将稳态时段tp代入截断函数C（t）即可求得截断系数C，其表达式为：

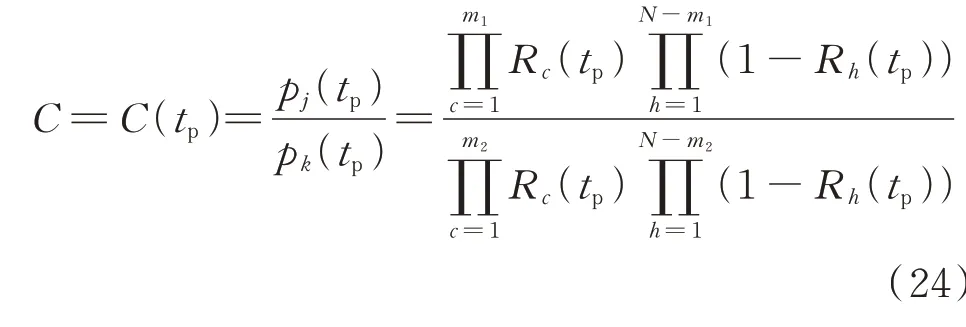
由图4 可知，即使设备的故障率、修复率不同，状态概率函数达到稳态的时间也仅在小范围内波动。本节设置了8 组数值差距在100 倍左右的故障率和修复率参数，稳态时段tp的范围在6.124 6 s 至9.499 2 s。待合并状态的转移率相近，稳态时段的波动范围进一步缩小。因此，对于不同状态只需计算一次稳态时段，避免了多状态系统稳态时段的重复计算过程，进一步提升了状态合并效率。详细数据见附录A 表A1。

2.3.4 截断系数法与马尔可夫过程的比较

2 种方法本质上都是求解系统状态概率，得到系统状态概率即可实现不同转移率情况下的状态合并。但由于马尔可夫过程求解效率较低，本文提出了截断系数法。提出截断系数的目的在于消去状态概率求解过程中的公因式，提高求解效率。本节基于马尔可夫过程和截断系数法求解系统状态概率，详细数据见附录A 表A2。由表A2 可知，对于图2所示的16 种系统运行状态，相较于马尔可夫过程，本文所提方法求解系统状态概率的平均误差率为3.547 5%。由此可知，截断系数法能够满足系统状态概率的求解精度要求。

3 基于状态合并的直流配电网可靠性评估

基于状态合并的直流配电系统可靠性评估首先列举直流电源的所有状态，然后根据本文所提方法实现状态合并，将合并后的电源状态与直流配电系统网架结构结合，利用状态枚举法［23］列举系统所有设备的N-1 阶故障。最后，根据线路、直流断路器等设备的可靠性参数（故障率γ、故障平均停电持续时间r、年平均停电时间U）计算可靠性指标。

直流配电系统负荷的平均停电频率（average interruption frequency，AIF）等于系统所有故障运行状态的频率之和。故障运行状态的频率等于状态概率乘以离开该状态的转移率［17］，表达式为：

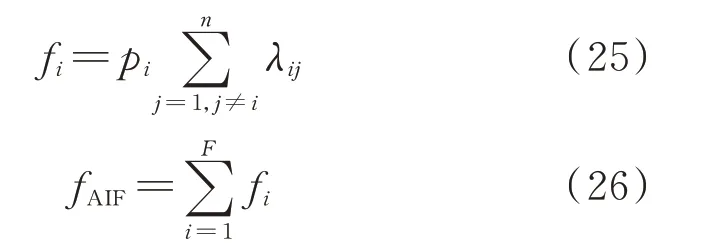
式中：fi为故障运行状态i出现的频率；n为系统运行状态数量；fAIF为AIF 的值；F为故障运行状态数量。

直流配电系统负荷的平均停电持续时间（average interruption duration，AID）等于系统全部故障运行状态的平均停电时间之和除以负荷的AIF。故障运行状态的平均停电时间等于离开该状态的转移率的倒数［17］。具体表达式为：

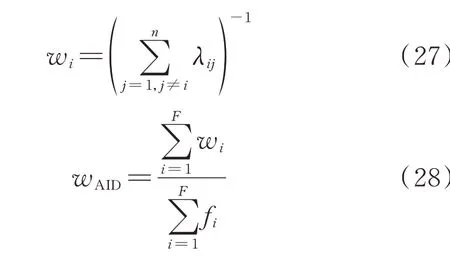
式中：wi为故障运行状态i的平均停电时间；wAID为AID 的值。

获取负荷可靠性指标后，根据配电系统可靠性指标计算方法［23］，进一步计算整个系统的可靠性指标，例如系统平均停电频率指标（system average interruption frequency index，SAIFI）、系统平均停电持续时间指标（system average interruption duration index，SAIDI）以及平均供电可用率指标（average service availability index，ASAI）。

4 算例分析

本文按照IEEE-RBTS BUS 6 建立直流配电系统，网架拓扑如附录B 图B1 所示。本算例将MMC视作直流电源，根据文献［11］可知，换流站内往往配置若干个小容量换流器作为子电源为直流配电系统供电。本算例的中压直流母线配有2 个换流站，每个换流站内有3 台额定容量为5 MW 的MMC，共计6 个MMC 作为中压直流母线电源参与可靠性评估，A 至F 为换流器编号。直流配电系统的电源配置及可靠性参数见附录A 表A3。

直流配电系统采用真双极接线方式，中压直流母线额定电压为±7.5 kV，低压直流母线额定电压为±375 V。系统共包含42 个直流变压器，80 个熔断器，9 个直流断路器，40 个负荷节点，总负荷容量为20 MW，共有2 938 户用户。为验证本文所提方法的正确性，基于上述理论编写C++程序，计算机处理器型号为Intel Core i5-4258U，内存容量为4 GB，系统类型为64 位操作系统。

为体现状态合并方法的优越性，算例划分了3 种场景，每种场景下的系统电源都有26=64 种状态，具体场景设置如下：

场景1：未计及状态合并。

场景2：状态分类合并，差额阈值δ1为0.01。

场景3：状态统一合并，差额阈值δ2为0.05。

4.1 未计及状态合并的直流配电系统可靠性评估

场景1 的直流配电系统可靠性评估通过马尔可夫过程列举直流电源的所有状态，将电源状态与直流配电系统网架结构结合，利用状态枚举法列举系统中的N-1 阶故障，并求解直流配电系统可靠性指标。根据上述求解过程得到的直流配电系统可靠性指标如表1 所示。直流配电系统的设备可靠性参数见文献［24］，具体如附录A 表A4 所示。

表1 未计及状态合并的直流配电系统可靠性指标Table 1 Reliability indices of DC distribution system without state merging

由表1 可知，直流配电系统可靠性指标包括负荷和系统2 个层面。由于场景1 未计及状态合并，因此，将其可靠性指标作为标准值，为4.3 节计及状态合并的可靠性评估效率与误差提供参考。

4.2 计及状态合并的直流配电系统可靠性评估

计及状态合并的直流配电系统可靠性评估是将系统电源状态按照本文所提方法，根据不同差额阈值实现状态合并。然后，基于4.1 节所述的可靠性评估方法计算可靠性指标。

状态合并选用的差额阈值决定了参与可靠性评估的系统状态数量。在3 种场景中，场景2 和场景3计及了状态合并。其中，场景2 的差额阈值δ1为0.01，是将正、负极母线电源状态分类合并；场景3的差额阈值δ2为0.05，是将所有电源状态统一合并。不同场景计及状态合并后的电源状态数量变化及可靠性指标如表2 所示。

表2 计及状态合并的直流配电系统可靠性指标Table 2 Reliability indices of DC distribution system considering state merging

由表2 可知，当差额阈值由0.01 增至0.05 时，场景2 的电源状态数量由64 降至12，场景3 的电源状态数量由64 降至7，并且相较于场景2，场景3 的可靠性指标有所降低。由此可见，差额阈值越大，参与可靠性评估的状态数量越少，并且还会导致可靠性评估出现误差。因此，差额阈值的选取应综合考虑可靠性评估的精度与效率，根据不同的应用场景选择合理的差额阈值。

4.3 计及状态合并的可靠性评估效率与误差

本节基于4.1 节和4.2 节直流配电系统的可靠性评估结果，进一步分析不同场景下可靠性指标的计算效率与平均误差率，分析结果如表3 所示。

表3 不同场景下可靠性指标计算效率与误差Table 3 Calculation efficiency and error of reliability index in different scenarios

由表3 可知，场景2 中负荷可靠性指标的平均误差率为0.55%，系统可靠性指标的平均误差率为0.84%；场景3 中2 类可靠性指标的平均误差率分别为5.65% 和5.07%。场景2 的误差率明显低于场景3，说明对于本算例，选用差额阈值δ1更为合理。计及状态合并后，场景2 的枚举状态数量由114降低至64，降低了43.86%，可靠性评估的计算时长由3.512 0 s 降至1.835 9 s，评估效率提升了47.72%。计及状态合并后的可靠性评估效率提升了约50%。由于实际配电系统的节点数量众多，因此，将本文提出的方法应用于实际配电系统能够节省的计算时间是可观的。

另外，本文通过改变直流配电系统电源数量建立16 种状态系统，并将本文所提方法应用于该系统的可靠性评估。由数据分析可知，虽然系统状态数量不同导致可靠性指标数值不同，但在可靠性评估效率与误差方面，16 种状态系统所得结论与64 种状态系统基本一致。16 种状态系统的具体数据分析见附录A 表A5 至表A8。

5 结语

本文提出一种基于状态合并的直流配电系统可靠性评估方法，该方法在保证计算精度的同时，有效提高了评估效率。

1）在应用场景方面，直流配电系统由于运行状态增多导致可靠性评估效率降低，本文首次将状态合并思想应用于直流配电系统可靠性评估。通过建立多状态直流配电系统的状态空间模型，将符合条件的系统运行状态合并，减少系统运行状态数量，提升多状态直流配电系统的可靠性评估效率。

2）从方法论的角度，本文将故障树分析法与马尔可夫过程结合，通过截断状态概率收敛进程确定截断系数。在保证精度的同时，提高了合并状态转移率的求解效率，实现了差异化转移率情况下的系统状态合并，拓展了状态合并在直流配电系统可靠性评估中的应用范围。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。