SAR performance-based fault diagnosis for electrohydraulic control system: A novel FDI framework for closed-loop system

Yng ZHANG,Shoping WANG,Jin SHI,*,Xinyu YANG,Jirui ZHANG,Xi WANG

a School of Energy and Power Engineering, Beihang University, Beijing 100191, China

b School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China

c Institute for Automatic Control and Complex Systems (AKS), University of Duisburg-Essen, Duisburg 47057, Germany

KEYWORDS Electro-hydraulic servo valve(EHSV);Fault diagnosis;Fuel metering unit;Performance degradation;Performance residual;Stability, accuracy, and rapidity (SAR)

Abstract Model-based fault diagnosis serves as an efficient and powerful technique in addressing fault detection and isolation(FDI)issues for control systems.However,the standard methods and their modifications still encounter some difficulties in algorithm design and application for complex higher-order systems. To avoid these difficulties, a novel fault diagnosis framework based on multiple performance indicators of closed-loop control system is proposed.Under this framework,a socalled performance residual vector is constructed to measure the differences between the real system and the nominal model in terms of system stability,accuracy,and rapidity(SAR)respectively.The criteria for quantification, normalization of the SAR residuals and the explicit mappings between the thresholds and the required performance are given. FDI can be easily achieved simultaneously by monitoring the normalized residual vector length and direction in the SAR performance residual space. A case study on electro-hydraulic servo control system of turbofan engine is adopted to demonstrate the effectiveness of the proposed method.

1. Introduction

Over the past decades, fault detection and isolation (FDI)issues have received much attention in both research fields and practical engineering applications due to the increasing demands of reliability in safety-critical systems.1-3As a result,numerous FDI methods have been reported for various dynamic control systems such as aerospace systems,4,5chemical processes,6and wind energy conversion systems.7Generally, control system faults will cause the performance degradation,mission failures or even major safety accidents,it is thus paramount to investigate the FDI techniques of control systems.

Traditional model-based fault diagnosis approaches, such as observer-based,8-10parity space-based,11and parameter identification-based12,13methods have been intensively investigated. Typically, these schemes are developed to detect faults by means of system output or parameter consistency checking between the real system and the reference model. To realize fault isolation, additional specialized algorithms, such as a bank of observers,14are also required to obtain the structure residual or the generalized residual. Despite the mature techniques, they may still suffer the practicality problems in engineering applications due to the difficulties in accurate modeling and algorithm designing of complex higher-order systems.

On the other hand, some of the existing observer-based approaches are designed for open-loop systems and will not be applicable for closed-loop systems due to the feedback control.15It was found that there is a trade-off between the control performance and the detection filter performance in feedback control systems.16Therefore, some hybrid FDI approaches combined the traditional observer-based method with artificial neural networks17to diagnose the actuators faults in closedloop control systems. Alternatively, recent developments have paid attention to the active fault detection problems by injecting auxiliary signals.18-21Despite the interesting results, there is still no a unified theoretical framework to design the auxiliary signals, therefore these schemes are far from mature and also have some limitations in practical engineering. Recently,some researchers have paid attention to the performance monitoring and evaluation methods in fault diagnosis and faulttolerant system.22-24However, to our best knowledge, few research efforts have been made to the multi-performance evaluation of the closed-loop system and use a multiple performance requirement-based method to diagnose system faults.

Generally, the fundamental task of a control system is to realize position, velocity, and force control with desired control requirements, such stability, accuracy, and rapidity (or speed of response) and so on.25-27In fact, different faults will have different influence on these performance requirement indicators,and different performance indicators have different sensitivities to the same fault, which may result in different or even wrong diagnosis results if we use less or only one performance indicator. For example, additive faults usually do not affect system stability, because these faults have no influence on system parameter matrix.Also,the decreased control accuracy caused by sensor fault cannot be discovered by the sensor output.28In order to detect and isolate more system faults,it is thus important to investigate such a multiple performancebased fault diagnosis framework.

Motivated by the above observations,we proposed a novel SAR performance based FDI scheme for the first time to deal with the fault diagnosis issues in closed-loop control systems.By contrast, we select the stability, accuracy, and rapidity(SAR) indicators of control system as the so-called multiple performance indicators. By constructing a three-dimensional normalized SAR residual space, we can easily detect and isolate different faults based on their different effects on these three performance indicator in this residual space.Specifically,we use the residual vector’s length to detect faults and use the residual vector’s direction to isolate faults, i.e. the so-called performance degradation trajectories.

The main contributions of this paper include: (1) the presented method provides a novel multiple performance-based FDI framework,which avoids the complex observer algorithm design of the conventional FDI approaches for complex higher-order systems and therefore has a better practicality in engineering, (2) under this unified framework, it provide a more comprehensive quantitative evaluation of the system running state and it can recognize more potential faults as long as they have influence on SAR performance whether they are additive or multiplicative, (3) the designed thresholds have explicit mappings with the required SAR performance requirements of control system, which facilitates the intuitive assessment of performance degradation and fault severity. It helps operators determine at what performance degradation level the fault-tolerant control measures should be taken to compensate for the SAR performance loss.

This paper is organized as follows.In Section 2,some useful preliminaries and the problem formulation are introduced.The multiple performance-based fault diagnosis schemes are developed in Section 3. A case study on electro-hydraulic fuel metering system of aircraft is given in Section 4, which is followed by the conclusions and future work in Section 5.

2. Preliminaries and problem formulation

2.1. Description of control system

For simplicity, consider a single-input single-output (SISO)closed-loop control system shown in Fig. 1, G(s) is the controlled object model, K(s) is the controller, r is the system input, y is the system output, d is the additive fault or disturbance, u is the control signal, and e is the error signal.

Coprime factorization of a transfer function is a kind of system representation form which will be adopted in our subsequent study.Let G(s)be a proper real-rational transfer function,then the coprime factorizations of G(s)can be written by29

where I is unit matrix with appropriate dimensions.

2.2. Problem formulation

As previously mentioned, SAR are the three basic control requirements of a control system. In other words, these three performance indicators are usually considered as the designed targets of a new control system. As shown in Fig. 2, system faults will cause some parameter changes,which definitely lead to some degradations in the SAR performance, and therefore the system cannot longer meet the control requirements.

To realize FDI from the perspective of fault effects, a natural idea is to discover the fault information by monitoring these degraded macro performances. Due to the fact that different faults usually have varying degrees of impacts on the SAR respectively,it is thus feasible to isolate the faults according to these influence differences.

Given the required performance vector

where γ is the system phase margin,esis the steady-state error,tsis the setting time and R is field of real numbers. They are indicators in stability, time-domain and frequency-domain control requirements, which are usually known parameters.There is no doubt that these required performances should be satisfied for a well-designed fault-free control system in practical engineering.

We can define a corresponding performance residual vector that indicates the performance differences between the nominal model and the actual system as follows

where δS, δAand δRdenote the performance residuals in SAR respectively.By doing so,it is guaranteed that the performance changes and the fault criticality of closed-loop system can be monitored and evaluated intuitively.

However, it is quite difficult to directly calculate the SAR performance of current system in an analytic way for complex high-order systems.Even though it is possible,there is actually no need to calculate the absolute performance values.Because FDI only needs information about the relative performance difference, i.e., how much has the SAR performance changed when fault occurs compared with the fault-free system. Therefore, there are three key problems need to be addressed to achieve FDI under the SAR performance-based diagnosis framework, they are (1) how to characterize and quantify the SAR performance difference, (2) how to normalize the SAR residuals, (3) how to determine the thresholds and achieve fault isolation according to the normalized residual vector.

In this paper, it is assumed that only the controlled object and sensor faults are considered, and the controller will not fail. Besides, the considered system faults are soft faults, i.e.,extreme faults such as the servo valve stuck and the open circuit of the sensor will not happen in the system.

3.SAR performance-based fault detection and isolation schemes

3.1. Characterization and quantification of SAR residuals

Consider a nonlinear system described by the following nonlinear differential equations

where f and g are nonlinear functions of system, x is system state vector, θ0denotes system parameters, and y0represents system fault-free output. When the system has a fault, the initial system parameter vector θ0will be changed to θ1,and correspondingly y0will be changed to faulty output y1.In general,y0can be the output of a linear or nonlinear reference model and y1can be obtained by sensor measurement.

The steady-state error esis a time-domain evaluation of the system performance. The accuracy residual δAbetween the actual faulty output and the nominal output can be easily expressed by

It is clear that the time-domain residual can be obtained just by the sensor measurement and the model-based reference output, while an actual model of the operating system is needed to evaluate the other two performance residuals δS,and δR.

For the system working at a certain operating point(x0, u0, θ0), where x0and u0are the initial system states and input, we can obtain a linearized frequency-domain reference model G0(s) by using the fault-free data. Let G1(s) be the actual model of the system,which describes the current inputoutput characteristics of the real system, i.e. G1(s) = G0(s)when the system is fault free, and G1(s) ≠G0(s) when there is a fault in the system.

By using the system input-output data, generally the controller output and the sensor measurement for SISO systems,the actual frequency-domain model can be easily identified according to the following least-squares cost function

where Ai, Bi, Ci, and Diare system matrices of the minimal state space realizations, subscript i = 0 denotes the fault-free case and i = 1 represents the identified actual model. Based on this state-space representation, we can easily calculate the right-coprime and left-coprime pairs of G1(s) and G0(s) as follows30the rapidity residual between the nominal model G0(s) and the actual model G1(s) is defined as follows:

Otherwise, δR(G0,G1)=1. Note that, the value δRis a supremum of the frequency response over the entire frequency domain and the value varies between 0 and 1.A greater rapidity residual value indicates a greater difference in closed-loop dynamics, so it is indeed a good indicator detecting faults of closed-loop system in this paper.

When the system has a fault, the dynamic response may change and the difference in rapidity can be evaluated by Eq. (12). Note that, a greater rapidity residual value δRindicates a bigger difference in system dynamic response, but it is just a concept of relative distance, and it is still uncertain that whether the degraded system gets faster or slower compared with the nominal case,so this problem will be addressed

With the coprime-based model representation, we can use the concepts of ν-gap and internal stability to evaluate the difference in rapidity and stability of closed-loop system. Specifically, the rapidity residual describes the performance difference in response speed, which is closely related to the position of poles in complex plane of a transfer function. To quantify this difference between two systems, we used the νgap metric theory, which has a clear frequency-domain interpolation. Compared with the operator norm, ν-gap metric measures the generalized distance between two models with respect to the closed-loop response difference. As the closedloop characteristics of two systems could be quite similar even though the norm of the difference between the two open-loop systems is very large,ν-gap metric is a better choice in evaluating the closed-loop differences.

Define

This indicator guarantees that all signals in a system are bounded provided that the input any signals to the closedloop system are bounded. The stability margin bGi,Kis the inverse of the maximum transfer gain and the value is between 0 and 1.If bGi,Kis close to one,it indicates that the system stability is being degraded due to the system faults.

Thus,when the system has a fault that influence the system stability,the stability residual between the identified model and the nominal model can be computed by Eqs.(14)-(15).If δSis a negative number, it shows that the current fault leads to a more stable system, so the normalization problems are also needed to evaluate the performance degradations, which will be addressed in the next section.

3.2. Normalization of SAR residuals and threshold functions

Fault thresholds have significant effects on the detection performance, but before designing the thresholds, the obtained SAR residuals need to be transformed into non-dimensional and normalized values,and. As aforementioned,the δRis a value between 0 and 1, and δSis a value from -1 to 1,but they may change within a very small range when fault occurs, which makes it difficult to detect these faults. On the other hand, in order to isolate more possible system faults,we used the normalized negative residuals to indicate the direction of performance degradations.As we all know,the closedloop SAR performance could be better or worse when a fault occurs.Therefore,when we consider the degradation direction information or the residual sign information, we can identify more faults that cause different performance changes. To deal with this problem, the critical fault severity factors (FSFs) are introduced to specify the critical performance degradations based on the initial Preq, as shown in Table 1.

In Table where α′and α′′represent the minimum and maximum degradation degrees with respect to the corresponding performance indicators. Based on this degradation factors,we can define the critical fault area boundaries of each performance, as shown in Fig. 3.The performance-related threshold design processes are given in the following contents in detail.

In practice, we can select appropriate FSFs shown in Table 1 to define a reasonable range of SAR performance degradation, as shown in Fig. 3. Namely, the minimum and the maximum performance degradations can be expressed by

For the rapidity residual, δRis a relative distance between two systems and an additional reference model is needed to establish the relationship between the setting time and the rapidity residual of the closed-loop system. Here we take a second-order open-loop model Gref(s)=ω2n/(s2+2ζωns) as a reference benchmark, where ωnis the equivalent natural frequency and ζ is the equivalent damping ratio. Then the time constant of the envelope of the transient response is 1/ζωnand typically ts=4/ζωncan be adopted to calculate the setting time.

According to Ref.29,the robustness stability margin is closely related to the phase margin, which provides the upper bound of the stability margin. i.e.,

Table 1 Control requirements and critical FSFs.

It is clear that these residuals have physical meanings and the thresholds have explicit mappings with the initial SAR performance requirements of control system. These advantages will help us to evaluate the fault severity intuitively, as shown in Fig. 3, we can divide the different fault cases into healthy state, minor fault, moderate fault, and major fault according to the size of residuals.

3.3. FDI in the SAR residual space

Consider the three normalized SAR residuals as the coordinates of a point in a three-dimensional space, then different faults with different magnitudes will correspond to the different points as well different space vectors in the SAR space.With these residual vectors,we can realize FDI easily by monitoring the vector length and vector direction.

where εland εdare the uncertainties of the vector length and vector direction respectively and they are identified according to the specific applications. In most cases, the monitored fault vector will not exactly the same to the theoretical value, so a reasonable tolerance helps to isolate fault accurately and quickly, as shown in Fig. 4.

It should be note that the fault database can be preestablished through simulation or experiment methods. In other words, the performance effects of the possible faults should be known quantitatively or qualitatively.On these conditions, the residual vector length can be used to detect faults and the vector direction can be used for fault isolation.Regarding this point, it will be illustrated in the subsequent case study.

4.Case study on fuel metering control system of turbofan engine

In this section,a case study on the fuel metering control system(FMCS) of aircraft turbofan engine will be introduced to demonstrate the effectiveness of the proposed method. The FMCS supplies the desired fuel flow to the engine combustor according to thrust demands during the flight. Suppose the engine is a two-spool turbofan,which consists of fan,compressor, combustor, low-pressure turbine (LP Turbine) and highpressure turbine (HP Turbine). Fig. 5 shows the schematic description of the FMCS of a turbofan engine, which mainly consists of fuel pump, electro-hydraulic servo valve (EHSV),fuel metering valve(FMV),controller and displacement sensor(LVDT).

4.1. Performance effects of the key components

The EHSV is used to control the FMV opening,which directly affects the fuel flow to the combustor. It is a two-stage nozzle flapper servo valve with sophisticated components,as shown in Fig. 6. The first stage has a flapper-nozzle type magnetic torque motor, the second stage has a precision ground four-way control spool and a mechanical feedback system.The displacement sensor measures the opening of the FMV and feedback the actual position signal to the controller.

The common degradations of EHSV and sensor faults and their effects on the system performance are summarized as follows.Note that,these fault influence can be analyzed in a theoretical way and we only give the qualitative conclusions due to the space constraints.

1) Sensitivity reduction of torque motor(Fault-1).This can be caused by the coil short-circuit and the irreversible degradation of the magnetic properties. The reduction of magnetomotive force will decrease the motor torque and therefore results in slower response of the fuel supply under the same input, but due to the feedback correction, the final position output will not be affected.

2) Partially nozzle clogging (Fault-2). This can be a result of fluid contamination due to the presence of some metallic debris. A partially clogged left nozzle (Fault-2L) will lead to an increased pressure in the left control chamber p1.Thus,the valve spool moves to a new equilibrium position with a constant steady-state error of the metered fuel flow.

3) Stiffness reduction of the feedback spring(Fault-3).This is a result of the normal component aging.A yield feedback spring will decrease the feedback force from the spool to the flapper, and consequently leads to an increase in the response as well as the instability of the FMCS.

4) Occlusion of the first-stage filter(Fault-4).This is due to the contaminant accumulation in the filter over time.This fault causes a larger pressure drop across the filter and a reduced filter flow capacity, which significantly affects the dynamic response and the stability of the FMCS.

5) Variation of the feedback sensor gain (Fault-5). This is due to the temperature drift or the loose connection cables of sensor. A varied gain sensor still results in an output error in the actual metering valve position as well as a changed dynamic response.

4.2. Nonlinear modeling and model reduction of FMCS

A high fidelity nonlinear mathematical model is essential to test the FMCS under different degraded conditions, some of which are practically impossible in real systems. Suppose ieis the input current,θais armature rotation angle,p1,p2are pressures in the left and right side of flapper valve respectively,p3is pressure in the flapper return chamber, xsis servo valve spool displacement and y is the opening of FMV,then the nonlinear model of FMCS is given by

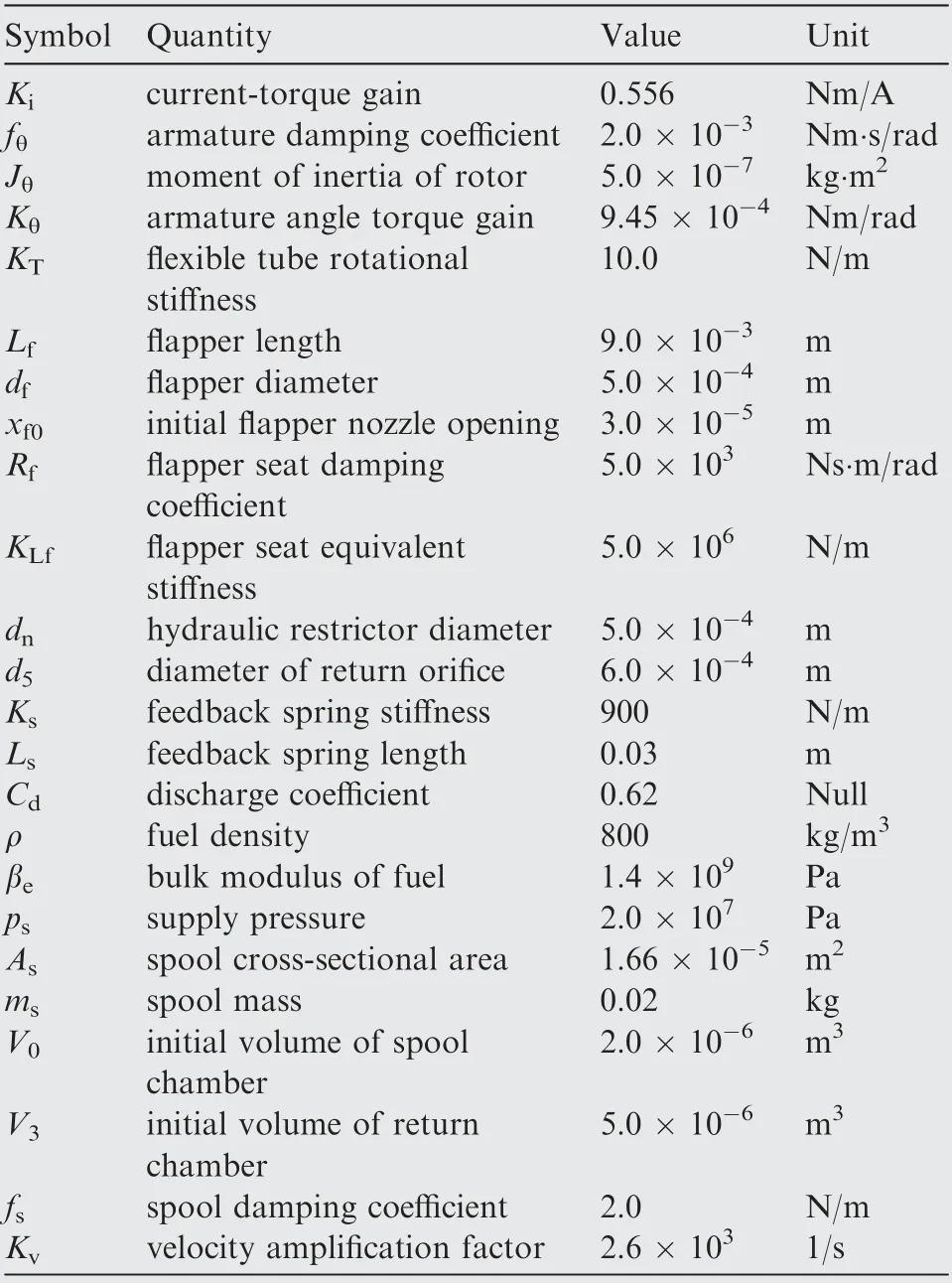
Table 2 Model parameters of the FMCS.

where all the relevant model parameters and values are given in Table 2.

We can consider this complex high-order nonlinear model as the ‘‘real” system and inject some faults to acquire the input-output data. Besides, the nominal model can also be obtained based on this model.Although the high-order nonlinear model includes all the parameters that describe the considered faults, a low-order linear nominal model around the FMCS working point is also needed to compute the performance residuals. Therefore, we discard the system states that have relatively smaller Hankel singular values such that

From the closed-loop frequency response in Fig. 7(b), the reduced-order model does not match well with the highorder model at high frequencies, but achieves a good approximation of below 1000 rad/s, which is far beyond the desired system bandwidth.To further verify the time-domain precision of the approximation model, the output responses are compared under the step and sine inputs respectively and the results are shown in Fig. 8.

From Fig. 8(a), the reduced model overall achieves a good match to the nonlinear model both in the transient and steadystate stages under the step input.The only difference is that the reduced model shows a slightly faster response due to the neglect of the low energy dynamic characteristics. According to Fig. 8(b), both the two models show a similar dynamic lag of around 0.025 s and there are slight tracking errors between the nonlinear model and the approximation model under the 6 Hz sine input. Hence, the reduced model can represent the nonlinear model around the working point without losing the major system characteristics.

4.3. Fault simulations and degradation analysis

The considered five fault modes in this study can be simulated by changing the corresponding model parameters in the nonlinear model. Fig. 9 shows the different degradations of the torque sensitivity with 15%, 30% and 45% respectively and the corresponding ν-gap based rapidity residuals between the degraded systems and the normal system.

It can be seen form Fig. 9(a) that the torque motor degradation has great impacts on the system rapidity, but has little effects on the steady-state error. The response time significantly decreases from around 0.1 s to 0.2 s as the degradation degree increases from 15% to 45%. Despite the slowed response, the steady-state error remains unchanged due to the compensation of the closed-loop controller. Meanwhile, a slower response generally indicates a greater stability margin,therefore the torque sensitivity reduction will make the system more stable.It is noticeable that the three ν-gap curves peak all at around 35 rad/s. A larger ν-gap value corresponds to a greater dynamic difference between the degraded system and the nominal model, which is consistent with the time-domain results shown in Fig. 9(a). Hence, the ν-gap metric can be a good rapidity indicator to evaluate the closed-loop control system.

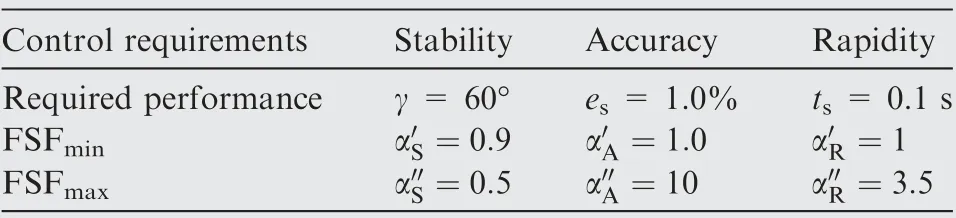
Table 3 SAR performance requirements of FMCS and FSFs adopted in this study.

The right nozzle (RL) and left nozzle (LN) of EHSV are blocked by 0.1%,0.2%respectively,and the results are shown in Fig.10(a). Fig.10(b)shows the 15%, 30%and 45%degradation of the feedback spring stiffness respectively. The filter contamination faults were simulated with 20%, 40%, 60%and 80% degradation respectively in Fig. 10(c). The sensor gain faults with the degradation of±5%and±10%were also simulated and the results are shown in Fig. 10(d).

It can be seen from Fig. 10(a) that the nozzle degradation has great influence on the steady-state accuracy, but has little impacts on rapidity and stability. The faulty systems have a constant setting time of around 0.1 s and a similar overshoot with the increasing nozzle degradations. In addition, the right nozzle degradation results in a positive output error, which is quite opposite for the left nozzle. In fact, a single partially clogged nozzle will lead to a new equilibrium position of the flapper, which corresponds to an additional spool output, as a result, only the static performance will be affected.

From Fig. 10(b), it is obvious that this fault will lead to a worse stability but a faster response.The maximum overshoot is approximately 20%when the degradation is 45%,because a fatigued spring provides a lower mechanical feedback force and thus the spool needs to move a greater displacement to achieve the same feedback force.

As shown in Fig.10(c),the system dynamics will be gradually delayed, but it is interesting to note that the system overshoot shows an upward trend in the initial degradation process and decreases when beyond a certain degradation level.The reason for this phenomenon is that the contaminative filter will result not only in a larger pressure drop across the filter, but also in a lower filter flow capacity. This is a comprehensive result impacted by the pressure drop and flow capacity of the filter.

According to Fig. 10(d), an increased sensor gain will lead to a faster response and a decreased gain will lead to a slower response, because the changed sensor gain corresponds to the changes in the reference input signal and the forward path transfer gain.

4.4. Normalized SAR residual space and degradation trajectories

For the FMCS,the required SAR control performance and the FSFs adopted in this study are given in Table 3.

According to the threshold functions designed in Section 3,we can calculate the fault normalized SAR thresholds and obtain the health region of FMCS, and the normalized SAR threshold vector is

To further analyze the residual distribution of different faults in the SAR residual space,i.e.the performance degradation trajectories,we performed a total of 350 fault simulations,with each fault mode being simulated for 50 different degrees of parameter degradation. All the monitored residual values and their spatial distribution and degraded projections in SA, A-R, and S-R planes are shown in Fig. 11 respectively.

It can be seen from Fig.11(a)that different faults generally show different distribution characteristics in the SAR residual space, except for the Fault-2 and Fault-5, which are mixed together, but actually they can be isolated by comparing the measurement output with the actual system outputs, which can be estimated by using a state observer or the inverse model of the turbofan engine.Regarding this point,relevant research will not be covered in this study. The other three fault modes have effects on both the stability and the rapidity.Specifically,Fault-1 and Fault-3 show a negative correlation between the stability and the rapidity, i.e., a system with a faster response shows relatively poor stability. However, Fault-4 shows a non-monotonic variation of the SR performance residuals, as shown in Fig.11(d),and the reasons for this phenomenon have been discussed earlier.

It should be noted that the SAR residual points are getting farther and farther from the original point in the SAR space as the performance degradation increasing and some residual points are so close from each other or even mixed together that we cannot determine the exact degradation degrees. But as long as any two SAR residual points on different trajectories are not overlapped or very close from each other, we can distinguish the faults and there is no need to determine the exact degradation value. In a word, all the considered actuator and sensor faults can be isolated intuitively according to the different performance degradation trajectories by using the proposed multiple performance-based method.

5. Conclusions

In this paper, a novel multiple performance-based fault diagnosis scheme for closed-loop control system is proposed. The presented normalized SAR residual vector is proved to be a good evaluation of the system performance degradation. To the best of authors’knowledge,this is the first trial to diagnose the multiple different faults of electro-hydraulic servo valve by using only one unified approach. The case study of FMCS shows that the proposed method has a good performance in diagnosing the electro-hydraulic servo system in the presence of internal faults of the EHSV and feedback sensor. By using this method, the performance degradation trajectories of different faults can be monitored in the constructed SAR residual space.This novel diagnosis framework can be applied to other closed-loop control systems including but not limited to the considered application. In the future work, we will be dedicated to the multiple fault diagnosis and the associated fault-tolerant control strategies to recover the system performance.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This study was co-supported by the National Science and Technology Major Project of China (Nos. 2017-V-0011-0062,2017-V-0010-0060), National Natural Science Foundation of China (51875014) and the Academic Excellence Foundation of BUAA for PhD Students.