Flow control of double bypass variable cycle engine in modal transition

Haoying CHEN, Changpeng CAI, Jiayi LUO, Haibo ZHANG

Jiangsu Province Key Laboratory of Aerospace Power System, College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

KEYWORDS Variable cycle engine;Two-dimensional CFD technology;Mode selection valve;Flow control;Modal transition

Abstract To study the change mechanism and the control of the variable cycle engine in the process of modal transition, a variable cycle engine model based on component level characteristics is established. The two-dimensional CFD technology is used to simulate the influence of mode selection valve rotation on the engine flow field, which improves the accuracy of the model. Furthermore, the constant flow control plan is proposed in the modal transition process to reduce the engine installed drag.The constant flow control plan adopts the augmentation linear quadratic regulator control method.Simulation results indicate that the control method is able to effectively control the bypass ratio and demand flow of the variable cycle engine,and make the engine transform smoothly, which ensures the stable operation of the engine in modal transition and the constant demand flow of the engine.

1. Introduction

Since the 1960s,a series of long-term research projects of variable cycle engine has been carried out in the United States, in which the technology has gradually matured.1-3Variable cycle engine could change the bypass ratio and related performance by adjusting the geometric parameters of adjustable components so that the engine has both low fuel consumption characteristic of high bypass ratio turbofan engine and high thrust characteristic of small bypass ratio turbofan engine.4Higher requirements for the new generation of engine design are put forward to achieve performance characteristics of the next generation multi-purpose military aircraft. It is required not only to have a higher thrust loading and the characteristics of high specific thrust as turbojet engine that could meet the requirements of the supersonic cruise,combat maneuver flight,and transonic, but also the characteristics of low fuel consumption as high bypass ratio turbofan engine to meet the requirements of the subsonic cruise, standby and air patrol.5-9Variable Cycle Engine (VCE) could meet the above two requirements, whose advantage is that it realizes two kinds of aerothermodynamic cycle modes of turbojet and turbofan on the same engine. Moreover, VCE makes the air-craft and engine have excellent characteristics in supersonic and subsonic flight. The change between the two modes is accomplished by modal transition, which could make VCE transform between large bypass ratio and small by-pass ratio.10,11

Plenty of research on VCE modal transition has been conducted around the world so far.12-15The engine performance under different mode selection valve opening has been analyzed.Zhou et al.studied the variable geometry characteristics of variable cycle engine and analyzed the control law of variable geometry adjustment variables under different working conditions.16Liu et al. simulated the modal transition of variable cycle engine and designed the modal transition scheme of variable cycle engine.17Wang et al. have studied the steadystate characteristics of variable cycle engine and the performance changes of engine during the modal transition. However, the mode conversion of VCE is a dynamic process.18In this process, due to the lag of response of aerodynamic parameters, the various principles of flow rate, bypass ratio,and total pressure recovery coefficient of internal and external ducts are different in time. If the mode transition process is only studied from the quasi-one-dimensional component level model, the accuracy of the model will be reduced. Furthermore, various principles will also make an influence on the research of variable cycle modal transition regulation schemes.Therefore, it is of great significance to study the dynamic model of variable cycle engine during the modal transition.19-22

Furthermore, in the research of modal transition control principle, all the existing control methods use open-loop control to adjust the adjustable components of VCE.23-26Although the engine could transfer smoothly, the flow matching problem between the engine and the inlet is not considered in the modal transition, which means the engine required flow could not keep constant in the modal transition process. This would increase the inlet spillage drag, which is unfavorable to the installation performance of engine.

In this paper, a component level model of double bypass variable cycle engine is established. The change of flow field during the modal transition is calculated by commercial software FLUENT, which includes the change of flow rate and total pressure loss. The results of two-dimensional flow field calculation are reflected in the VCE component level model by the interpolation function.Meanwhile,a constant flow control plan is proposed, which is used in the process of modal transition to make the engine transform smoothly. Compared with the existing technology, the constant flow closed-loop control technology ensures that the engine required flow remains constant, which reduces the engine spillage drag and improves the engine propulsion efficiency.

2. Double bypass variable cycle engine modeling

2.1. Principle analysis of variable cycle engine

In order to study the change law of engine cycle parameters and performance parameters in the dynamic process of VCE modal transition, the double bypass variable cycle engine is selected as the research object and the corresponding model is established.The geometric parameters of adjustable components are shown in Fig.1,which includes fan guide vane angle(αf), Core Drive Fan Stage guide vane angle (αCDFS), highpressure compressor guide vane angle (αc), low-pressure turbine guide throat area (AtL), area of mode selection valve(AMSV),area of FVABI(A125),area of RVABI(A163)and nozzle throat area (A8).

The addition of adjustable components makes the variable cycle engine have the characteristics of modal transition that the engine could transform between single bypass model and double bypass model. The characteristics make the variable cycle engine not only meet the military requirements but also realize the vision of supersonic air-liner. However, too many adjustable components also bring difficulties to the establishment of VCE numerical model. These are mainly reflected in the influence of mode selection valve and bypass ejector adjustment on the engine flow field parameters, which could not be determined in the process of engine component level modeling,and should be determined by the flow field calculation. Especially in the process of modal transition,due to the lag of aerodynamic parameter response, the changes of fan exit flow and bypass ratio are not only related to the flow area. Therefore,this paper studies the influence of the adjustable components’geometric parameters on the VCE performance parameters during modal transition, which is the key to establish VCE mechanism model and design VCE modal transition control plan.

2.2. Calculation of flow field in mode transition

To analyze the influence of MSV on engine performance during modal transition,the part structure of variable cycle engine is given in Fig. 2, which includes mode selection valve, front mixer and compression components.The key section numbers are as follows,Cross-section 2 is the inlet of fan,Cross-section 21 is the exit of fan root (inlet of CDFS), Cross-section 22 is the exit of fan tip (inlet of MSV), Cross-section 225 is the exit of secondary bypass, Cross-section 125 is the exit of FVABI,Cross-section 15 is the inlet of front mixer, and Cross-section 24 is the exit of CDFS. The secondary bypass flow of the engine would mix with a part of the CDFS outlet flow in the front mixer, which would enter the mixing chamber through the RVABI and mix with the core flow.The opening and closing of mode selection valve directly determine the operating mode of the engine.

To accurately simulate the part structure of VCE,the commercial software FLUENT is used to calculate the steady twodimensional viscous flow field. The turbulence model is the SST model in k-ω. According to the part structure, the model adopts the grid drawn by ICEM,and is used as the calculation model of modal transition. When checking the grid quality,more than 95% of the grid numbers are above 0.995 (the grid quality is 0-1,which is good above 0.9).The number of meshes is determined by the size of the model. The boundary conditions at the inlet of calculation domain are calculated by the VCE component-level model. The inlet flow rate is 50 kg/s and the total temperature is 433.737 K. The static pressure at the exit of secondary bypass and the inlet of CDFS is 308,307 Pa and 330,000 Pa respectively. In the process of calculation,the flow field change of mode selection valve from 0°to 30° is calculated, whose change takes 5° as a calculation point. In the calculation, there is no slip on the wall, and the wall is adiabatic.The rotational symmetry boundary condition is selected for the axis of symmetry,and the steady calculation is used for the flow field under different MSV’s rotation angle.

In this paper,the effects of different MSV’s opening degrees on flow field parameters such as flow rate and total pressure of core and bypass are compared. The steady flow fields are calculated when the angle of mode selection valve θ are 0°, 5°,10°, 15°, 20°, 25°, and 30° respectively. The model adopts the grid drawn by ICEM,and when checking the grid quality,more than 95% of the grid numbers are above 0.998 (the grid quality is 0～1, which is good above 0.9). The number of meshes is determined by the size of the model. In the model,the mesh of the model boundary layer uses refined grids to ensure the accuracy of the model calculation. The results of FLUENT calculation are shown in Fig.3.It could be seen that in the process of closing MSV, the airflow of the secondary bypass is gradually compressed, which causes most of the airflow to flow into the CDFS and results in the change of the core and bypass flow field. What’s more, the compressed flow in the secondary bypass increases the Mach number of the flow field and changes the front and back pressure,which results in the total pressure loss.

2.3. Component level model for variable cycle engine

Furthermore, in order to analyze the model, the relationship between the flow rate and total pressure of each section and the angle of the mode selection valve is given in Table 1. It could be seen from the table that the exit flow of the secondary bypass decreases with the increase of the MSV’s angle,and the total pressure also decreases.

According to the data in Table 1,the fan bypass ratio α and the total pressure recovery coefficient σ of the secondary bypass could be further calculated.

where m225is the secondary bypass exit flow, m24is the exit flow of CDFS, Pt225is the exit total pressure of secondary bypass, Pt22is the inlet total pressure of secondary bypass.According to the above calculation formula, the relationship between fan bypass ratio α, total pressure recovery coefficient of secondary bypass σ,and the angle of mode selection valve is obtained, which is shown in Table 2.

Based on the relationship in Table 2, two-dimensional interpolation is used to correlate the fan bypass ratio and the total pressure recovery coefficient of secondary bypass with the angle of the mode selection valve.

where k represents corresponding numbers for different θ.For example, when k = 1, θ is 0°, and when k = 2, θ is 5°and so on. α[k] and σ[k] represents the fan bypass ratio and the total pressure recovery coefficient of secondary bypass at different MSV’s angles.

Therefore,the fan bypass ratio and the total pressure recovery coefficient of the secondary bypass could be obtained from Eq.(3).According to the above formula,the relationship functions between α,σ and altitude H,Mach number Ma and θ are established, where f1(·), f2(·) are interpolation functions of fan bypass ratio and total pressure recovery coefficient of secondary bypass respectively.

where m22is the fan tip exit flow,A225is the maximum opening area of the secondary bypass, and AMSVis the actual opening area caused by MSV.

Table 1 Relationship between parameters of part structure and MSV’s angle.

Table 2 Relationship between α, σ and MSV’s angle θ.

Although Eq. (6) reflects the relationship between the flow rate and the flow area, it is not reasonable. The calculation of the secondary bypass flow is not only determined by the opening area of the MSV. The flow field at the exit of the fan and the inlet of the secondary bypass ought to be considered. The results of area calculation would affect the change of engine parameter performance in the process of modal transition,which reduces the credibility of the model.Fig.4(a)shows the comparison of fan bypass ratio with MSV angle based on CFD flow field calculation and MSV’s actual opening area calculation. It could be seen from the figure that the results of CFD simulation and area calculation are different in the process of θ change. The relationship between MSV’s angle and fan bypass ratio is nearly linear. While in CFD calculation, when θ changes initially, the decrease of bypass ratio is relatively slow, and with the increase of θ, the decrease of bypass ratio is more obvious. Fig. 4(b) shows the variation of the σ calculated by CFD with the change of θ.

In this paper, the effect of different incoming flow conditions (by changing the inlet flow rate and pressure) on flow field parameters is considered, which is shown in Fig. 5. The flow rate changes from 30 kg/s to 70 kg/s and the inlet total pressure changes from 26,100 Pa to 35,100 Pa. It can be seen from the figures that the incoming flow condition would affect the flow field with the change of MSV’s angle. The total pressure recovery coefficient of secondary bypass σ would increase with the increase of inlet pressure and the decrease of the inlet flow rate. However, it has little influence on the bypass ratio.

Therefore, Eq. (4) is substituted into the component level model of the variable cycle engine and the CDFS flow balance equation ε is replaced as follows.

In the above research,the CFD two-dimensional numerical flow field calculation is considered in the component level model. Meanwhile, according to the relationship between α,σ and θ,the fan bypass ratio and total pressure recovery coefficient of secondary bypass are modified,and the performance parameters of the engine are recalculated.The model has both the original real-time performance and the CFD flow field analysis of the modal transition, which improves the confidence and accuracy of the model.

The component-level model of double bypass variable cycle engine is established based on the principle of aerothermodynamics. The modeling process can be referred to as Ref.27. Eight initial guess values are selected in the model, which includes low-pressure rotor speed Nl, highpressure rotor speed Nh, fan pressure ratio coefficient Zf,CDFS pressure ratio coefficient ZCDFS, compressor pressure ratio coefficient ZC, high-pressure turbine equivalent mass flow m41,cx, low-pressure turbine equivalent mass flow m45,cx, and fan airflow root/tip ratio Xht. Nl, Nhalso represent the fan rotor speed and the high compressor rotor speed.

During the whole engine modeling, eight coupling equations are selected according to the flow continuity, static pressure balance and power balance.

In this paper, the model takes the ground condition as the design point. The eight coupling equations contained by the steady model are shown below.

The power balance residual functions of high-pressure rotor and low-pressure rotor are shown as follows.

where m41,cxis the high-pressure turbine initial guess flow and m41,cis the calculated flow, m45,cxis the low-pressure turbine initial guess flow and m45,cis the calculated flow.

The static pressure balance residual functions of fan,bypass outlet, and nozzle throat are shown as follows.

These equations could be solved by the Newton-Raphson method, through which the characteristic and performance parameters are obtained.

The data required to build the component level model is generated based on Gasturb software, which has a relatively perfect design process and reliable simulation accuracy.Fig. 6 and Fig. 7 show the characteristic diagram of CDFS and the characteristic diagram after the guide vane angle of CDFS changes. m24cis the equivalent mass flow of CDFS,πCDFSis the pressure ratio of CDFS and ηCDFSis the efficiency of CDFS.Fig.6(a)shows the characteristic diagram of CDFS pressure ratio and equivalent mass flow when αCDFSis 0°, in which the corresponding lines of each relative converted speed of CDFS are marked in detail. Fig. 6 (b) shows the change trend of the characteristic line when αCDFSchanges from 0°to -30°. Similarly, Fig. 7 shows the characteristic diagram of CDFS efficiency and the variation trend of characteristic line with αCDFS. The angle of the low-pressure turbine guide θtLis adjustable. Assuming that the throat of the turbine guide is in a critical or supercritical state, the area of the lowpressure turbine guide affects the turbine flow characteristics,which are expressed by the angle of the guide. That is to say,when the angle of turbine guide increases or decreases by 1°,the flow through the turbine increases or decreases by 1%.

The comparison of calculation results between Gasturb software model and component-level model at design point is shown in Table 3, where Ma is the flight Mach number, H is the flight altitude,πf,πc,πtH,πtLare respectively the pressure ratio of fan, high compressor, high pressure turbine and low pressure turbine. ηf, ηc, ηtH, ηtLare respectively the efficiency of fan, high compressor, high pressure turbine and low pressure turbine. mfis the fuel mass flow rate, F is the engine thrust, S is the specific fuel consumption of the engine, Tt4is the total temperature of combustion, A8is the nozzle throat area, A125is the area of CDFS bypass, A163is the area of bypass outlet, A6is the area of core stream mixer entry,Ma125is the Mach number of CDFS bypass, Ma225is the Mach number of the secondary bypass, Ma163is the Mach number of bypass outlet, Ma6is the Mach number of core stream mixer entry. It could be seen from Table 3 that after giving the input parameters, such as flight state, fuel flow of combustion chamber and afterburner, nozzle throat area,and so on, the values of section parameters and performance are the same, which indicates that the established component level model has certain reliability.

3. Control principle analysis of double bypass variable cycle engine

3.1. Analysis of constant flow control principle

Engine control plan is the top requirement of engine control system design,which is of decisive significance for control system design, and largely determines the steady-state and transient performance of engine. The engine dynamic and steadystate control plan plays an important role in the whole flight process.Reasonable control plan design can effectively reduce the maintenance times in the engine’s service life and save the operation cost. Based on the special structure of the variable cycle engine, this chapter focuses on the control plan of the variable cycle engine during the mode conversion, and proposes a constant flow control method,which uses the fuel flow of the main combustion chamber to control the fan speed and the nozzle throat area to control the fan pressure rise divided by fan inlet total pressure.

Due to the difficulty in directly measuring mass flow with the engine in real time, the engine mass flow must be inferred through the known thermodynamic relationships with other measurable parameters within the engine. The most practical method of measuring mass flow is to relate it to the engine operating line on a fan map, which is shown in Fig. 8. Tt2 is the fan inlet total temperature,Tstdis the ambient temperature under standard condition,m21cis the fan equivalent mass flow.As can be seen in Fig.8,if the controller is able to regulate the engine’s performance to the same corrected rotor speed and pressure ratio of fan for a given throttle setting, the engine’s corrected mass flow would be maintained. Therefore, under the same flight conditions, the engine inlet flow can remain unchanged.

Based on the above analysis and the actual situation,it can be seen that the mechanical rotor speeds are easily measured by a magnetic pickup located in proximity to a passing gear tooth, the fan inlet and outlet static pressure are measured by the pressure sensors, and the fan inlet total pressure could be calculated through the flight altitude and Mach number.In this paper, the Augmentation Linear Quadratic Regulator Algorithm(ALQR)is used to realize the modal transition constant flow control method of variable cycle engine,which takes the constant flow rate at the engine inlet as the control objective. The fan speed and compressor speed are the state variables, the fuel flow, and nozzle throat area are the control variables, the fan speed and the ratio of fan static pressure change to the fan inlet total pressure are the output variables.

According to the above model, the constant flow control method of modal transition is studied. The engine fan speed Nland the ratio of fan static pressure change to the fan inlet total pressure ΔP/Pt2are obtained from the model.The calculation formula of fan static pressure change ΔP is as follows.

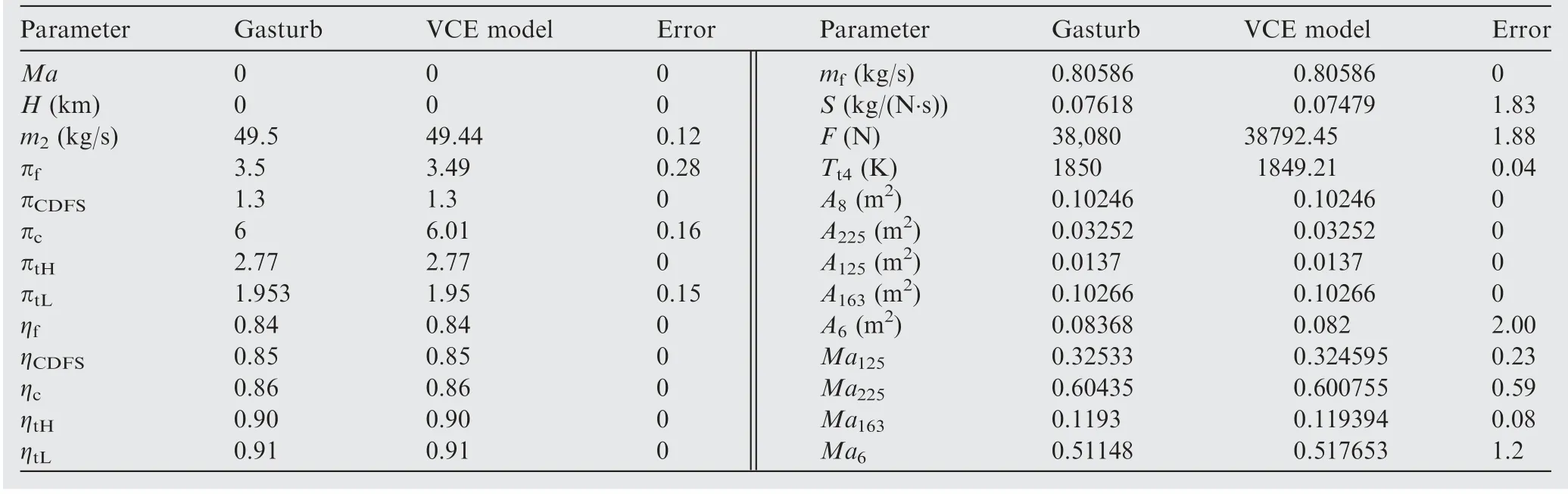
Table 3 Data comparison of VCE design point.

where k is the ratio of specific heats.

During the constant flow control, if the inlet condition of the engine remains unchanged,it means that the fan exit Mach number and P22could be controlled unchanged. According to the above formula, it can be concluded that the total pressure of fan exit Pt22remains unchanged.Furthermore,the fan pressure ratio could be kept unchanged. Therefore, it can be seen from Fig. 8 that under the condition of constant fan pressure ratio and fan rotor speed, the relative conversion flow of the fan could also remain unchanged,and the calculation formula of engine inlet flow is shown as follows,

where Pt2dsis the fan inlet total pressure at design point, Tt2dsis the fan inlet total temperature at design point.

It can be seen from the Eq.(21)that the constant flow control can keep the engine inlet flow unchanged on the premise of keeping the engine inlet condition unchanged. According to the above analysis, the reason why the control plan does not directly control the fan pressure ratio is that if the boost ratio is directly controlled, the engine would be limited at the operating point, which may cause the engine to run unstable in other flight segments. In other words, the aircraft cannot fly within a large envelope. The constant flow control can ensure that the engine could work stably at different operating points,and keep the engine flow unchanged when changing the bypass ratio at the same operating point.

The constant flow control plan of variable cycle engine in modal transition is shown in Fig. 9. According to the flight condition, the Pilot Lever Angle (PLA) and the N1request logic, the fan rotor speed command is determined. In the control system,the rotor fan speed is controlled by the fuel flow of the main combustion chamber. Based on the real fan speed measured by the sensor, the error between the real speed and the control command is taken as the input. Similarly, according to the flight condition, PLA and ΔP/Pt2request logic, the command of ΔP/Pt2is determined. In the control system, ΔP/Pt2is controlled by adjusting the nozzle throat area.Based on the real static pressure of the fan inlet and outlet measured by the pressure sensor, the static pressure difference of fan inlet and outlet is calculated, and ΔP/Pt2could also be calculated.Similarly, the error between the data measured by the sensors and the control command is taken as the input.The two inputs get the actual fuel command and nozzle section adjustment command through ALQR controller, which forms a complete closed-loop control.

To further highlight the influence of constant flow control on engine performance, this paper adopts the traditional engine control plan to the variable cycle engine model and compares it with the constant flow control plan. The control system is shown in Fig.10.Pt6is the total pressure of low pressure turbine. In the traditional control plan, the fan rotor speed and engine pressure ratio have the greatest correlation with engine thrust,so the traditional control plan uses the nozzle to control the engine pressure ratio EPR,which is the difference between the traditional control plan and the constant flow control plan.

3.2. Control plan of variable cycle engine

According to the variable cycle engine model established above, the corresponding parameter variables are selected to establish the state variable model of double bypass variable cycle engine. The expression of the VCE state variable model is as follows.

where A, B, C, D are the state variable matrix, low rotational speed Nland high rotational speed Nhare selected as state variables x, fuel flow mfand nozzle throat area A8are selected as control variables u, Nl, and the ratio of fan static pressure change to the fan inlet total pressure ΔP/Pt2are selected as output variables y.

4. Simulation results and analysis

The simulation is carried out at flight conditions of Ma =1.2 and H = 10 km to verify the reliability of the proposed constant flow control method in the modal transition, where the variable cycle engine changes from double bypass mode to single bypass mode.Fig.12 shows the adjustment scheme of each component in the transition process.Fig.12(a)shows the MSV closing adjustment scheme, while Figs. 12(b)-12(d) show the fuel flow mf, nozzle throat area A8, CDFS angle αCDFS, highpressure compressor angle αc, RVABI area A163, and lowpressure turbine guide angle θtLadjustment scheme respectively.

To ensure the smooth operation of the engine in the conversion process, it is necessary to reduce the CDFS angle and the high-pressure compressor angle to increase the engine core flow. Meanwhile, it is necessary to increase the low-pressure turbine guide angle to increase the turbine demand flow and reduce the RVABI area to ensure that the engine has no inverse flow.The control method is used to adjust the fuel flow and nozzle throat area to keep the inlet flow and bypass ratio unchanged. Similarly, the adjustment scheme of each component in the transition process from single bypass to double bypass is also given, as shown in Fig. 13.

Figs. 14(a) and 14 (b) respectively show the effect of Control method 1 and Control method 2 in the modal transition from single bypass to double bypass, where m25represents the compressor inlet flow.It could be seen from the figures that the constant flow control method is able to improve the flow change of variable cycle engine during the modal transition,which reduces the inlet spillage drag and improves the engineinstalled performance. Fig. 14(c) and 14 (d) respectively show the effect of two control methods in the modal transition from double bypass to single bypass. The modal transition process with Control method 1 can better control the flow rate to keep constant.Fig.14(e)and 14(f)respectively show the percentage change of total flow corresponding to each control method in two mode transition, which is the ratio of the change of fan inlet flow to the initial inlet flow.The modal transition process with Control method 1 can better control the flow rate to keep constant.The modal transition process with Control method 1 can better control the flow rate to keep constant. To further analyze the robustness of the control method, the total flow variation is analyzed in the process of modal transition. It can be seen from Figs. 14(e) and 14 (f) that Control method 1 could stably control the flow in the process of mode transition.The maximum fluctuation range of flow is about 1%, which indicates that the control system has good robustness. However, the Control method 2 has a great fluctuation in the flow and the maximum fluctuation range reaches about 5%.

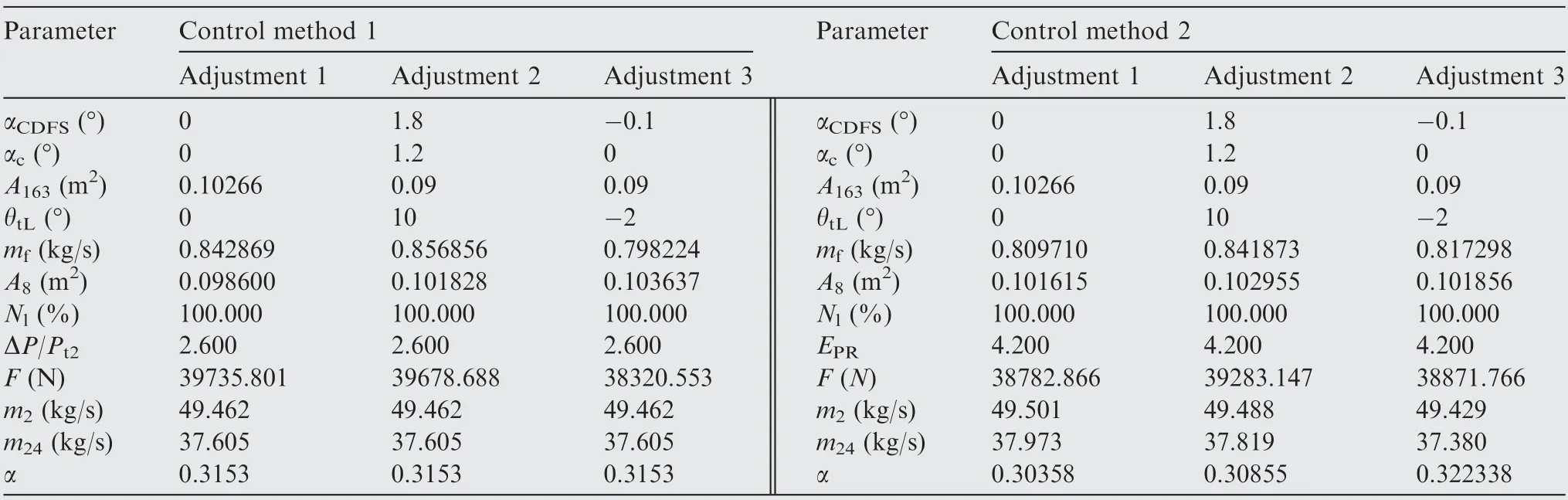
Table 4 Data comparison of VCE control method.

Fig. 15 shows the change of engine low and high rotational speed, turbine inlet temperature, and compressor surge margin during the transition process of variable cycle engine,

where SMlis the surge margin of fan, SMCDFSis the surge margin of CDFS, SMhis the surge margin of high compressor. In the figure, the dotted line represents the mode transition from single bypass to double bypass and the solid line represents the mode transition from double bypass to single bypass. It could be seen from the figures that in the modal transition, the low rotational speed is controlled at speed 100%, and the high-pressure speed is about 102.5% in the single bypass mode, which does not exceed the limit speed.The inlet temperature of the turbine does not exceed the limit value, and there is no surge in the compressors. Therefore,the modal transition control plan could ensure the stable operation of the engine.

5. Conclusions

This paper is concentrated on the modal transition and control principle of double bypass variable cycle engine.With the analysis and simulation results,the following conclusions could be drawn.

(1) A variable cycle engine model based on component level characteristics is established.The two-dimensional CFD technology is used to simulate the influence of mode selection valve rotation on the engine flow field, which improves the accuracy of the model.

(2) The ALQR control method is adopted in the constant flow control method and the method could ensure that the fan bypass ratio and inlet flow of the engine remains unchanged.Furthermore, the results show that the control algorithm has good robustness.

(3) The control method is able to effectively control the bypass ratio and demand flow of engine and make the engine transform smoothly, which ensures the stable operation of the engine in the process of modal transition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This study was co-supported by the National Science and Technology Major Project, China (No. J2019-III-0009-0053)and the Advanced Jet Propulsion Creativity Center, China(No. HKCX2020020022).