Effects of chemical energy accommodation on nonequilibrium flow and heat transfer to a catalytic wall

Shunliang ZHANG, Zhihui WANG

School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China

KEYWORDS Catalytic reaction;Energy accommodation;Heat transfer;Nonequilibrium flow;Stagnation point

Abstract The accurate prediction of the aeroheating performance of hypersonic vehicles requires more detailed modeling of the catalysis process, rather than merely employing a catalytic coefficient.In this paper,the theoretical modeling,as well as the direct simulation Monte Carlo method,is used to preliminarily study the incomplete chemical energy accommodation effects,that is,only a part of the potential energy released in the heterogenous recombination reaction is transferred to the surface, while the remaining is retained as the vibrational energy of the desorbed molecule.An integrated model is proposed to describe the contribution of each energy mode in the rarefied nonequilibrium heat and mass transfer process. Based on the model and several Damko¨hler numbers,an analytical formula is derived,and is also shown to compare well with the numerical results.On account of the incomplete accommodations of the chemical and vibrational energy on the wall,a variation up to 20% is observed in predicting the stagnation point heat flux under typical nonequilibrium flow conditions. This study could enrich our understanding of the nonequilibrium heat transfer phenomenon and also shows a potential practical value.

1. Introduction

The hypersonic cruise/glide vehicles usually suffer a highintensity aeroheating experience during the long-time flight,leading to the demand for a more precise prediction of its aerothermal environment. Hypersonic flow and aeroheating features are largely affected by the high temperature real gas effects,1such as the excitation of the vibrational energy and the dissociation-recombination reactions of the molecules.The effects of Gas-Surface Interactions (GSI), including the catalysis and energy accommodation,also show increasing significance especially under the rarefied flow conditions.

From a microscopic point of view, the transfer of the heat to the wall is accomplished via the GSI, i.e., the translational,rotational, and vibrational energy of the molecules are transferred to the wall via collisions between molecules and the wall.In addition,the catalytic recombination reaction of atoms also takes place on the wall,releasing the chemical potential energy to induce the catalytic heating.Under typical flight conditions,a considerable portion of the freestream energy is converted into the chemical energy due to the dissociation reaction.Because the recombination reaction in the boundary layer is usually non-equilibrium or even frozen, a large percentage of atoms could reach the wall surface, making the catalytic aeroheating potentially become the dominant contribution to the total heat load.2-4Consequently,in order to develop a reliable prediction method, it is necessary and also important to reassess the catalytic aeroheating process by considering some detailed effects, such as the incomplete Chemical Energy Accommodation (CEA). In some numerical studies,5,6the incomplete CEA has been found to generally play only a limited role in the blunted body reentry problems,but it may play an important role in the present rarefied flow surrounding the non-ablation leading edges of the new generation hypersonic cruise vehicles. It would be meaningful to include the incomplete CEA in a theoretical modeling framework for fast estimating its effect in the engineering practice.

A parameter popularly used to evaluate the catalysis activity is the catalytic coefficient, also called the recombination coefficient,

which represents the probability of the catalytic reaction when an atom collides with the wall, with Nrbeing the number of atoms that recombine and Ntotthe total number of atoms which impinge onto the surface. The catalytic coefficient, with a value between 0 and 1,is a material parameter in relation to the material-gas pairs, the wall temperature and even the surface history.Materials with a low catalytic coefficient, such as Ultra-High Temperature Ceramics (UHTC),7are preferred in the thermal protection design since they significantly decrease the aerothermodynamics load.

In most studies of catalytic heating,8,9it is assumed that all the chemical energy will be transferred to the wall as long as a catalytic recombination event occurs. However, the CEA process is likely incomplete in the catalytic reactions (either the Eley-Rideal or Langmuir-Hinshelwood mechanism).10,11Usually, only a part of the chemical potential energy released by the catalytic reaction is directly transferred to the wall, while the remaining is stored in the recombinated molecules,10,12-15mainly in the vibrational mode16,17and possibly a little in the electronic mode.17For the sake of simplicity, only the vibrational excitation of the recombined molecules is considered in this paper, and without loss of generality, the analogous method can be used to deal with other situations.18

It is clear that the heat flux will be reduced due to the incomplete CEA, and a CEA coefficient

has been introduced to characterize this phenomenon, where qc,totis the chemical energy flux released from the catalytic reaction, and qcis the accommodated heat flux. Similar to the catalytic coefficient γ,β also ranges from 0 to 1,depending on the gas-material categories, temperature and the catalytic reaction mechanism.19In the flow reactor experiment,10the catalytic and CEA coefficients are determined under the assumption that particles collide with the wall only once.Obviously, the catalytic heating is proportional to γe=γβ which is called the equivalent or energy transfer catalytic coefficient.20

Generally, in many theoretical and numerical works, when referring to the catalytic coefficient, it actually means the equivalent catalytic coefficient γe, and it is reasonable to use the combined parameter rather than two independent ones in predicting the catalytic heating under highly rarefied or continuous flow conditions.13,11As mentioned above, for the free molecular flow, such as those in the flow reactors,10the catalytic heating is proportional to γe=γβ obviously. For the continuous flow cases,two factors need to be considered.First,the boundary layer in the continuum flow tends to be chemically equilibrium due to the high collision rate of molecules,and thus the catalytic property of the wall has little impact on the aero-heating performance. Second, even if the boundary layer is chemically nonequilibrium in some situations, still because of the high collision rate,the unaccommodated energy carried by the reflected molecule will be quenched in the nearwall flow field via collisions between molecules, or be transferred to the wall by the subsequent, multiple collisions between molecules and the wall, and comprehensively, the total heat flux is insensitive to the incomplete CEA property of the wall.Fig.1 demonstrates the microscopic process of catalytic recombination (Eley-Rideal mechanism, for example),incomplete CEA, homogeneous collision and Vibrational Energy Accommodation (VEA) or possible diffusion. In the figure, hd,evdenote the characteristic dissociation energy and the vibrational energy, respectively. The VEA coefficient21,22is defined as

in which the superscripts ‘‘i” and ‘‘r” denote the incident and reflective molecule,respectively,and‘‘w”denotes the limit case

where the molecule is fully accommodated,or namely,in thermal equilibrium with the wall.

By contrast, in the rarefied nonequilibrium flows, the quenching effect is not sufficient enough because of the relatively low collision rate. A vibrationally excited molecule reflected from the wall could diffuse to the downstream region or move far away from the wall without losing much of its vibrational energy. Therefore, the incomplete CEA will show a non-negligible influence on the aero-heating performance under this situation. In a numerical study, Fertig et al.5have shown the significant influence of CEA on the catalytic heating experiments in plasma wind tunnel facilities23where the flow in the test section is usually highly dissociated, and uncertainties by a factor of two have to be expected in measurements of the catalytic coefficient.Herdrich et al.24have discussed the importance and the difficulty of separating the catalytic recombination coefficient and the energy accommodation coefficient,and the current state of art is still that the complete CEA assumption, or the equivalent catalytic coefficient has to be used in most theoretical or numerical studies because of the complex physics and missing experimental data.8,9But in fact,as shown in the previous studies,25-27the typical flow surrounding the sharp leading edge of the hypersonic cruise vehicle is exactly in the rarefied and nonequilibrium state.It could fail to predict the catalytic heating performance by considering only the equivalent recombination coefficient.

In order to enrich our understanding of the CEA and to quantitatively estimate its influence on the aero-heating, it is necessary and also meaningful to carry on a theoretical modeling study of the CEA phenomenon to extend and improve the theoretical framework3,28of catalytic heating. Similar modeling studies have been shown successful in assessing the VEA effects on heat transfer to the stagnation point29and the flat plate.30

As a preliminary study, this paper focuses on the incomplete CEA effects on the heat transfer in the Stagnation Point Boundary Layer (SPBL) which is one of the most typical and important examples in the engineering practice.Following our previous theoretical modeling studies on the chemical nonequilibrium stagnation flow of nitrogen gas, more details of the surface properties, such as the incomplete CEA and VEA on a partly catalytic wall, are added and considered in a uniform integrated framework. Contributions of different energy modes are carefully distinguished based on several Damko¨hler numbers,and the quenching of the vibrationally excited molecules reflected from the wall is specifically analyzed under various rarefied and nonequilibrium flow conditions.Corresponding to the physical analysis, a modified theory is introduced to estimate the influence of CEA on the total heat flux.The Direct Simulation Monte Carlo(DSMC)method31is also employed to calibrate and validate the analytical formula within a practical range of flow parameters.

2. Physical analysis and theoretical modeling

As mentioned above,the incomplete CEA phenomenon occurs in the heterogenous recombination reactions on the catalytic wall surface. As a result, there must be plenty of dissociated atoms produced in the flow field,and many of them could travel across the boundary layer to reach the wall surface.One of the typical situations providing this environment is the rarefied nonequilibrium flow induced by a hypersonic sharp leading edge flying in a moderate-density gas.27,28In the following,we will first describe this flow model, briefly review the ideas on predicting its heat transfer features, and then analyze the complex GSI process to introduce the influence of CEA in an integrated model.

In the real air flow related to the reentry problem, much more complicated effects, such as the exchange reaction and the ionization, will be encountered. However, in the flow over a sharp-leading vehicle flying in the near space,the most significant real gas effects are the vibrational excitation and the dissociation-recombination reaction of molecules. In a theoretical modeling study, it is popular and practical to study these effects by using a pure diatomic gas model, considering that air,as a mixture of nitrogen and oxygen gases,could also be treated as an equivalent diatomic molecular gas.32Furthermore, the phenomenological models (specified reaction efficiency and accommodation coefficient) are preferred currently in describing the gaseous and surface reactions,and their reasonability and reliability could be verified via comparisons with the numerical results.Of course,in the accurately numerical studies, more detailed chemical/physical processes like the non-Boltzmann energy distribution and the state-to-state model33have been considered. The coupling between the heat transfer and the material properties’ variation34,35is another interesting problem, but will not be discussed in this paper. The velocity slip and temperature jump boundary conditions are not taken into account here, because of the negligible tangential velocity at the stagnation point and more importantly that the present study gives a relative rather than an absolute correction particularly referring to the incomplete accommodation effects.

2.1. Flow field features

Generally, the sharpened nosetip and wingtip of a near-space hypersonic cruise/glide vehicle can be modeled, respectively,as a slightly spherically blunted cone and a cylindrically blunted wedge. Fig. 2 shows the flow structure of a typical two-dimensional stagnation flow of the thermochemical nonequilibrium gas (only half is given due to symmetry), where Δ,δ,RNand Ma∞indicate the standoff distance of the bow shock wave,the thickness of the SPBL,the radius of curvature of the leading edge and the freestream Mach number, respectively. The flowfield behind the shock can be divided into two zones. Zone I between the shock wave and the outer edge of the boundary layer is dominated by the endothermal processes, including the vibrational excitation and molecular dissociation due to the high temperature. By contrast, Zone II in the SPBL clinging to a cooled wall is dominated by the exothermal processes, including vibrational de-excitation and the homogeneous recombination of atoms. The maximum Degree of Dissociation (DoD) is legitimately assumed to be reached at the outer edge of the SPBL. Besides, the complex catalysis, CEA and VEA processes take place on the wall,and the details will be discussed later in this section.

The above physical and chemical phenomena are accompanied by the energy transfer and conversion along the stagnation streamline which is illustrated in Fig. 3. ˙E∞, ˙Eδ, ˙Ediffand qsare the energy flux from the freestream, at the out edge of the SPBL,diffusing to the downstream and at the wall,respectively. The input energy flux is ˙E∞≈(1/2)ρ∞V3

∞, where ρ∞and V∞are the density and speed of the freestream, respectively. Across the shockwave, the kinetic energy is converted into the thermal energy, and then a part of the energy is converted into the vibrational (υδ˙Ev) and chemical potential energy (αδ˙Ed) in Zone I. Here, υδand αδare the Degrees of Vibrational Excitation (DVE)29and dissociation at the outer edge of the SPBL, respectively; ˙Ev=ρ∞V∞Rθvand ˙Ed=ρ∞V∞Rθd, with R,θvand θdbeing the specific gas constant,the vibrational and chemical characteristic temperatures,respectively. For the nitrogen molecule,31θd=113500 K and θv=3371 K. Oppositely, in the boundary layer, some of the chemical energy(αrec˙Ed)could be converted back into the thermal mode, and some vibrational energy (υde˙Ev) into the translational and rotational modes,where αrecis the change of DoD due to the homogeneous recombination reaction,and υdeis the change of DVE due to collisions between the gas molecules.

Similarly, the energy conversions on the surface can be measured by αcat, i.e., the DoD variation due to the catalytic recombination reaction, and υacc, i.e., the DVE variation due to the vibrational accommodation.The analogy between them has been discussed by Luo and Wang,29but the incomplete CEA effects has not been touched, and it is the main topic to be analyzed below.

2.2.Previous framework of modeling nonequilibrium SPBL heat transfer

Prediction of the stagnation point heat flux is always a very important problem in either the theoretical studies or engineering practice.Fay and Riddell’s classical theory2of the equilibrium SPBL shows that the total heat flux is insensitive to where the atoms recombine, and the heat flux of equilibrium SPBL(all atoms recombine in the flow field) is almost identical to that of the frozen SPBL clinging to a fully catalytic wall (all atoms recombine on the wall). Goulard3introduced a theory cosidering the effect of the partly catalytic wall on the frozen SPBL heat transfer, and it was shown that the total heat flux can be divided into two independent parts, qλand qD, which represent contributions of the thermal energy(including translational, rotational, and vibrational energy) conduction and the catalytic recombination reaction, respectively. Similar to Goulard’s work, but more concisely, Rosner36also showed the similarity of mass and heat transfer.Wang et al.28generalized this framework to cover the case of chemical nonequilibrium SPBL which is equivalent to a virtual frozen SPBL with a modified flow state at its outer edge to reflect the homogeneous recombination effect.

Mathematically, the conduction heat flux28can be written as,

The various DoDs in the above formulas can be calculated based on several Damko¨hler numbers which are defined as ratios of the characteristic time scales of different processes.38For examples, Dar=τf/τrecand Dac=τf/τcatwere introduced to indicate the nonequilibrium degree of the homogeneous and heterogeneous recombination reactions,3,26,28respectively,

where τf,τrecand τcatare the characteristic times of the flow,gas-phase recombination and catalysis, respectively.Da ≫1,Da=O(1) and Da ≪1 indicate an equilibrium,nonequilibrium and frozen flow state, respectively. Since the change of the DoD is apparently proportional to the reaction rate, or in other words, inversely proportional to the corresponding time scale, it is convenient to write

For brevity, the expressions of Darand αδcan be found in Refs. 26,27, and Dacin Ref. 28.

Eq.(3)has been shown robust and reliable in estimating the nonequilibrium SPBL heat transfer to an arbitrarily catalytic wall, and it provides a basal framework which could be extended to analyze the incomplete VEA and CEA effects on the aeroheating performance. In fact, the VEA effect has already been specially studied under this framework by Luo and Wang.29

2.3. Incomplete accommodation of chemical and vibrational energy

Physically speaking,the energy transfer from the gas to a solid wall is accomplished by the collision and accommodation process. The efficiency of the thermal and chemical accommodation could significantly affect the heat transfer features.According to their relaxation time scales, the translational and rotational modes of molecules could be considered as in equilibrium, and the corresponding energy to be completely accommodated to the wall.39By contrast, the nonequilibrium of the vibrational and chemical processes should be considered, and the VEA and CEA on the wall are usually incomplete40-42,10,12-15in the engineering practice. In the following,the abovementioned framework will be extended to cover the incomplete CEA as well as the VEA effects.

Fig. 4 shows the really complex process of the molecular energy transfer and conversion near the wall.The heat conduction due to the translational and rotational energy accommodation (Process I) is essentially the same to that in the abovementioned original framework, and that due to the VEA (Process II) needs a special treatment if σv＜1.The heat transfer due to the catalysis now involves even more details since only part of the recombination energy can be directly transfer to the wall before the molecule is desorbed. As an extension of Eq.(2),the catalytic heat flux can take the form as

When tracked carefully, this part of energy must go to one or several of the following optional destinations.

(1) Migration: diffusing to the downstream or other region with the molecule;

(2) VEA: being transferred to the wall via the subsequent collisions between this molecule and the wall (Process II′)

(3) Quenching or namely, gas-phase de-excitation: being converted into the translational and rotational energy via collisions between the gas molecules (Process V),and then diffusing or accommodating again(Process I′);

(4) Kickback:being converted back into the chemical energy via re-dissociation due to the possible energetic collisions between molecules (Process VI).

Now the task is to assess the relative impact of each possible option, and to mathematically describe how much it contributes to the total heat flux. Inspired by our previous work,a feasible and also practical idea is to compare the characteristic time scales to introduce Damko¨hler numbers, and by using these flow criteria to measure the corresponding phenomena and even to design a quantitative prediction formula.Since the chemical relaxation is generally much slower than the thermal relaxation near a cooled wall,it is acceptable to ignore the ‘‘kickback” effect. Alternatively, under another logic, this omission could also be explained by that the model considers only the net output of the vibrational energy after the ‘‘kickback” having been offset. The key point here is to predict the VEA’s contribution to the total heat flux, as long as the quenching effect which could be significant if the SPBL is not highly nonequilibrium.

In studying the VEA effect on the SPBL heat transfer,Luo and Wang29have introduced a formula which is similar to Eq.(5).Its form can be extended to describe the current VEA process, i.e.,

where τv,aand τv,ddenote the characteristic time scale of the vibrational accommodation on the wall and the de-excitation in the flow field, respectively, and Dav,a=τf/τv,aand Dav,d=τf/τv,dare the corresponding Damko¨hler numbers which measure the nonequilibrium degrees of the two processes. It was found29that

where the free stream Reynolds number Re∞=ρ∞V∞RN/μ∞,and μ∞,T∞and Twdenote the free stream viscosity, the temperature of the free stream gas and wall, respectively. Dav,acan be considered as an analogy with the catalysis Damko¨hler number28As for the calculation of Dav,d, with the flow time scale τf=RN/V∞, the characteristic time of vibrational relaxation can refer to the Landau-Teller equation43

T should take the characteristic value in the relaxation process.In the present problem, it is reasonable to introduce a characteristic temperature based on the unaccommodated chemical energy,with a correction from the VEA effect.Among various options, a concise but practical expression is found to be

within the parameters’ range of interest.

Now, after a detailed analysis, the heat flux due to the recombination reaction of atoms can be writen as

As for the heat conduction in Fig. 4, most of the previous studies2,3,44,27assumed complete VEA or thermal equilibrium in studying the chemical nonequilibrium effects. Luo and Wang29studied the incomplete VEA effects, but didn’t consider the chemical reactions.Currently,besides the vibrational excitation due to the catalytic recombination and incomplete CEA(Process IV),the molecules enterring the SPBL have been vibrationally excited in the post-shock high temperature region. This part of vibrational energy, measured by the DVE υδin Fig.3,is secondary when compared with the translational and rotational energy or the chemical energy,since the main component of the gas mixture is dissociated atoms.However, it is still necessary to approximately estimate the incomplete VEA of this part of energy (Process II), in order to acquire a comprehensive description of the complex CEA and VEA problems.

A precise prediction of the energy distribution among different thermal degrees of freedom seems extraordinarily tedious and impractical.Alternatively,similar to the Ideal Dissociation Gas (IDG) model,45-47the vibrational energy is assumed to account for a fixed proportion, 1/6 at present, of the molecular total thermal energy at the outter edge of the nonequilibrium SPBL. It is equivalent to suppose that the vibrational degree of freedom is half excited at the equilibrium limit state. According to the conservation of energy,

where the four terms on the right hand side denote, respectively, the chemical energy flux, the pressure energy flux, the thermal energy fluxes of the atoms and molecules at the equilibrium limit. As a result, the vibrational energy flux is approximately,

The traditionally used theory in the engineering practice can be considered as a limit version of Eq.(18)under the thermochemical equilibrium assumption (Dar≫1 and Dav,d≫1)or the full catalysis (Dac≫1) and complete accommodation(β=σ=1,Da ≫1) assumptions, which takes the form as

3. Results and discussion

A series of DSMC simulations have also been carried out to verify the above analysis under different nonequilibrium conditions and wall properties. The presently employed is an improved version of Bird’s DS2V program39,48which is recognized reliable to simulate the nonequilibrium chemical reaction flows.49The quantum model of the vibrational energy is adopted to deal with the dissociation and recombination reactions. The reflection of molecules from the wall is assumed to be fully diffusive.The flow conditions can be found in Table 1.The baseline simulation (Case 1) is conducted under the flow condition Ma∞=25,ρ∞=4×103kg/m3, RN=1 mm, and the equivalent catalytic coefficient γe=γβ=0.1. If γeis fixed,a low CEA coefficient indicates a high value of the intrinsic catalytic coefficient, for example, β=0.1 and then γ=1. Previous experimental measurements10,5have shown that the value of β could be lower than 0.3 for the nitrogen atoms on metals or SiO2. More accurate data is expected to be derived from the molecular dynamic calculations and more delicate experiments.

3.1. Flow field results

In order to have a macroscopic view of the incomplete accommodation, we would like to demonstrate some flow field features before directly turning to the heat flux. Fig. 5 shows the translational temperature profiles along the stagnation streamline under the typical CEA and VEA coefficients. Basically, all the profiles are approximately consistent with each other. However, the case with the low accommodation coefficients(β=0.1,σv=0)has a lower efficiency of energy transfer to the wall, and so more energy stays in the flow field, leading to a little higher boundary layer temperature and a slightly larger shock wave standoff distance.This situation is more clearly displayed by the vibrational temperature profiles in Fig.6.Significant difference could be observed near the wall, but the influence hardly travels beyond the SPBL. The unaccommodated vibrational energy will be partly converted into the translational and rotational modes, i.e. the nonequilibrium vibrational de-excitation (Process V in Fig. 4), resulting in an increase of the corresponding contributions to the total heat flux, as will be shown later. Furthermore, as shown by the DoD (α) profiles in Fig. 7, the chemical state of the gas near the wall is mainly determined by the catalytic coefficient γ rather than the equivalent γe, and it is dependent little on the incomplete accommodation, because the dissociation reaction needs much longer time and is almost frozen near the cooled wall under the current flow condition.This result also identifies the reasonableness of ignoring the ”kickback” effect (Process VI in Fig. 4). The main flow features shown here are similar to those predicted by a nonequilibrium Navier-Stokes code.5

3.2. Stagnation point heat flux

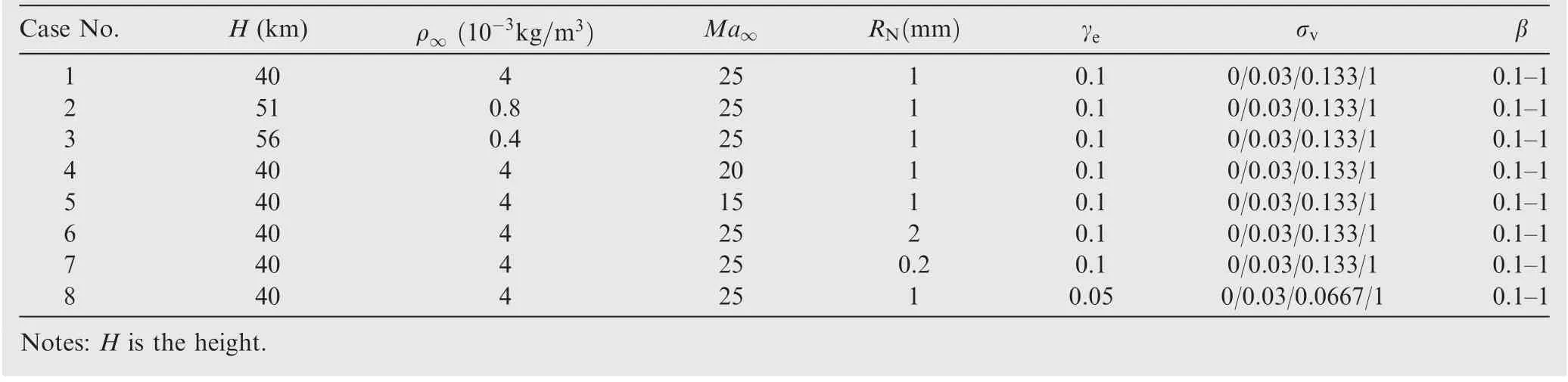
Table 1 Parameters in DSMC simulation (T∞=Tw =300 K).

In order to quantitatively show the effects of incomplete CEA and VEA,the variation characteristics of the normalized heat flux are demonstrated in Fig.9 where the scattered points are the DSMC results and the curves are the predictions by Eq.(20). In Fig. 9, it can be seen that even if the equivalent catalytic coefficient is fixed, the stagnation point heat flux will vary with the CEA and VEA coefficients. If the VEA coefficient is low enough, there could be a heat flux reduction of more than 20% as the CEA coefficient decrease. However, if the VEA coefficient is sufficiently high, the heat flux will even rise roughly 5%due to the higher energy transfer efficiency of VEA, as mentioned above. This feature is consistent with that found in Fertig et al.’s work5which showed that within the reentry regime of relevance the heat flux variation due to the influence of the CEA is within the band of inaccuracy of typical heat flux measurement techniques. Simulation cases with the different Mach number (Case 4) and equivalent catalytic coefficient (Case 8) essessentially show the same features,although a little poor agreement is observed for the lower Mach number cases. Hence, it is apparent that only a single equivalent catalytic coefficient is not enough, and an accurate heat transfer prediction requires the CEA and VEA coefficients as well.It may partly explain the vast scatter of the catalytic property data from heat flux measurement experiments.

Especially,when the VEA coefficient is approximately comparable to the equivalent catalysis coefficient, or more precisely, σv=4γe/3 as shown here, the heat flux is roughly invariable as the CEA coefficient varies, which is consistent with the prediction of Eq. (21). As σv＞0.03, the relationship between the heat flux and β is approximately linear, but when σv＜0.03, a nonlinear dependence appears because the gas phase de-excitation of the vibrational energy is becoming important. The vibrational energy is converted into the translational and rotational energy, and then transferred to the wall, slowing down the decrease trend of the heat flux. The analytical formula introduced in this paper not only qualitatively captures the variation characteristics of the heat flux,but also gives an approximately quantitative, reasonable prediction of various influence factors.

Finally, results of all the cases listed in Table 1 are shown together in Fig. 10 whose abscissa and ordinate are the right and left hand side terms of the Eq. (20) respectively. It can be observed that all the data points roughly fall in one line.The comprehensive agreement between the analytical prediction and DSMC results is reasonable, considering that so many complex mechanisms are included in one single formula under an integrated framework. As a preliminary study, the method proposed here could be used to estimate the aeroheating performance under the nonequilibrium flow conditions and complex gas-surface interaction.

4. Conclusions

This paper presents a comprehensive description and theoretical modeling of the complex gas-surface interactions particularly including the incomplete accommodations of the chemical energy and vibrational energy. Under a uniform framework, the effects of various thermal and chemical nonequilibrium processes are characterized and measured by the introduced Damko¨hler numbers.It was found that the traditional method employing a single parameter, i.e., the equivalent catalytic coefficient, is no longer effective to accurately predict the nonequilibrium heat transfer to partly catalytic walls with the incomplete chemical and/or vibrational energy accommodations. This situation is noteworthy in studying the near space flight of the new generation hypersonic vehicles.For the typical equivalent catalytic coefficient γe=0.1,the prediction error of the stagnation point heat flux could range from less than 5% (σv=1) to over 20% in the limit cases(β=0.1,σv=0). An approximately analytical formula was deduced to quantitatively estimate the complex nonequilibrium flow and incomplete accommodation effects.

This preliminary study indicates the importance of the detailed modeling of the complex gas-surface interaction,and could be seen as an extension of our previous work on the rarefied nonequilibrium flow and heat transfer. It also shows potentially practical value in explaining the scatter in the catalytic calorimetric measurements experiments and in fast predicting the aero-heating performance of the hypersonic vehicles.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Nos. 11672292 and 12072343), the Youth Innovation Promotion Association of Chinese Academy of Sciences (No. 2017490), and the Strategic Priority Research Program (B) of Chinese Academy of Sciences (No.XDB22040202).