Nonlinear system identification framework of folding fins with freeplay using backbone curves

Shuaishuai LIU, Rui ZHAO, Kaiping YU, Bowen ZHENG

Department of Astronautical Science and Mechanics, Harbin Institute of Technology, Harbin 150001, China

KEYWORDS Backbone curves;Folding fin;Freeplay nonlinearity;Harmonic approximation;Indirect estimation;Output-only identification

Abstract Due to wear and manufacturing tolerance, the freeplay is unavoidable in the hinges of folding fins,which exerts significant effects on the aerodynamic characteristics.This paper proposes a backbone-curve-based framework for the dynamical identification of folding fins containing the freeplay nonlinearity. With no need to measure the input force signal and the response signals of nonlinear related Degrees of Freedom (DOFs), the proposed method is more direct and elegant than most existing nonlinear identification approaches, and it contains three steps: Firstly, the underlying linear model of the folding fin structure is obtained through the modal test on its linear sub-parts,and then,the harmonic approximation solves the analytical expressions of the backbone curves of measurable DOFs.Secondly,response data measured from the sine-sweep test are used to extract the fitting points of backbone curves for these DOFs. Finally, the curve fitting approach is applied to identify the freeplay parameters. A series of numerical experiments verify the effectiveness of the proposed method. A real-life folding fin structure is also employed to illustrate how the method can be applied.These examples demonstrate that the identification framework can give an accurate dynamic model of the folding fin structure.

1. Introduction

The folding fin has been widely used to save storage space and to improve the transport efficiency of air vehicles. However,due to wear and manufacturing tolerance, the freeplay or clearance is unavoidable in the hinges of folding mechanisms that present the characteristics of nonlinear stiffness.1,2The nonlinearity that results from this mechanism is impossible to eliminate completely, which exerts significant effects on aerodynamic characteristics.3-5For instance,Yang et al.6conducted the wind tunnel test and numerical analysis on folding fins, and they found that the vibration divergent speed increases with the increase of freeplay angle. Thus, it is necessary to obtain an accurate dynamic model of the folding fin structure.

For parametric methods, Crawley et al. proposed the Force-State Mapping (FSM) method14that could be utilized to identify the strong-nonlinearity, and later, they used it to identify the nonlinear joints.15Kim et al. employed the FSM method to identify the nonlinear restoring force model for the displacement and velocity of a deployable control fin.16Then they established an elaborate reduction model of the deployable control fin based on substructure synthesis methods.17However, the FSM method demands the experimental data of the displacement, velocity, acceleration, and applied force of the nonlinear relating Degree of Freedoms (DOFs),which restricts its applications. Marchesiello and Garibaldi proposed the Time-Domain Nonlinear Subspace Identification(TNSI)method18that could be used to estimate the parameters of strong nonlinear systems.For instance,the nonlinear structure involves clearance. Sun et al.19utilized TNSI to identify the rotational freeplay of an all-movable fin. Another identification method, called the Conditioned Reverse Path (CRP)method,was developed by Richards and Singh.20Wu et al.utilized the CRP method to identify the hinge nonlinearity of a folding fin structure.21Meanwhile, they pointed out that the responses of the DOFs with nonlinearity should be measurable or estimable. In fact, all the above-aforementioned methods need the experimental data of the nonlinear relating DOFs,but sometimes these response data are not all measurable.

For nonparametric methods, Ma et al.22employed direct parameter identification estimation to obtain a 2-DOF lumped mass model of the folding fin structure.Recently,many neural network methods have been introduced in aerodynamic analysis.23,24Although these nonparametric methods do not have to use the response data of the nonlinear related DOFs,they usually establish surrogate or black-box models of the real-life structures,and as a result,the identified models can be applied mainly to qualitative analysis of the aerodynamic characteristics.

Therefore, a parametric nonlinear identification method with no rigid requirement on response data needs to be put forward for the folding fin structure. The Backbone Curve(BC)25-27of nonlinear systems can be employed to achieve this method. For a single-DOF conservative system, the BC is the relationship between the amplitude of vibration of a typical periodic motion and its period or frequency. For multi-DOF systems, the definition of backbone curves can be viewed as an analogy of the single-DOF system. London˜o et al.28proposed a nonlinear identification framework based on the BC.They identified the nonlinear stiffness of a wing-nonlinear pylon-inspired test piece by fitting the analytical BC with the experimental BC. However, this method needs to calculate the analytical expression of BCs that is not easy to obtain,especially for non-smooth nonlinearity. In addition, the Resonant Decay Method (RDM)29,30that they used to extract the experimental BC is merely suitable for weak damping systems.For the folding fin structure,because of the impacting effect of the rotation hinge, the structural energy is lost very quickly,and hence, the RDM is not suitable.

In this paper,a backbone-curve-based system identification framework of folding fins with freeplay is proposed. The harmonic approximate method is employed to obtain the analytical expression of BCs,and the sine-sweep test is performed to extract the fitting points of BCs.Subsequently,the corresponding nonlinearity identification problem is transformed to fit the BCs of the measurable response points, achieving indirect estimation.

2. Preliminary and notations

2.1. Dynamical model of folding fins

Fig. 1 shows a typical folding fin structure. When unfolded,two stoppers in front and back (red marker in Fig. 1(a))can prevent the relative rotation between the inboard and outboard fins. Its dynamical model can be graphically represented as in Fig. 1 (b), in which three node-pairs join the inboard and outboard fins together. Ux-, Uy-, Ux-, Ry-, and Rz-DOFs of the three node-pairs stay the same, respectively.Because of wear and manufacturing tolerance, the hinge of the folding fin has the freeplay nonlinearity. Two freeplay springs simulate this nonlinear characteristic and separately join the Rx-DOF of the node-pairs at left and middle. In consideration of the similarity of their local structures, these two springs should have the same nonlinear parameters. Fig. 2 demonstrates the restoring force model of these two freeplay springs, and their mathematical functions can be expressed as.

2.2. Analytical expression of backbone curves

The BC represents the unforced and undamped response and indicates the resonant characteristics of its corresponding forced and damped system.27Therefore, the unforced and undamped form of Eq.(2) is used to compute the BCs:

He flew into a dreadful rage when he saw them, and screamed out, Oh, you fools! the river and bridge were they! Go back and bring them to me at once, or it will be the worse for you

where ω=2πf is the angular frequency.Secondly,the Describing Function Aanalysis (DFA)31,32is utilized to obtain the

To qualitatively analyze the accuracy of the above approximate analytical expression, we investigate a single-DOF freeplay oscillator (see Example 1 in Ref. 33). The result of the Incremental Harmonic Balance (IHB) method is chosen as a comparison, and three harmonic terms (ωt, 2ωt, and 3ωt)are taken into consideration. Fig. 3 presents the calculated BC results. As can be seen, for a large amplitude motion, the proposed method has the same precision as IHB, but for a small amplitude motion, there exists error. Therefore, when using the proposed method in nonlinear identification, the external excitation should be big enough so as to obtain a more accurate identification result.

2.3. Identification framework of folding fins with freeplay using backbone curves

After obtaining the analytical expression of the BC of the folding fin, a complete identification framework can be summarized in Fig. 4. The folding fin is a typical structure with local nonlinear characteristics. Its freeplay nonlinearity only exists in hinges, and most parts of it are linear. Therefore,the identifying work can be divided into three steps. Firstly,the linear modal analysis is applied to the linear sub-parts of the folding fin, and the modal updating method is used to get an accurate finite element model (M and K in Eq.(8)) of the outboard and inboard fins. Secondly, the sine-sweep test is carried out on the full fin structure, and the fitting points of BCs are obtained by extracting amplitude-frequency jump points of sine-sweep data.Finally,Eq.(8)is utilized to fit these points, and as a result, the nonlinear parameters knand δ can be identified.

3. Numerical verification

In this section,a series of numerical experiments are employed to verify the proposed identification framework.Firstly,a sinesweep numerical experiment is conducted to verify the feasibility to extract the fitting points of BCs from the sine-sweep displacement, velocity and acceleration data, respectively.Secondly, noise tests are performed to verify the noise robustness of the proposed identification framework.Finally,numerical experiments with various clearance parameters δ are tested to demonstrate the identification ability of the proposed framework.

Fig. 5 shows the Finite Element Model (FEM) of the numerical experiment employed in this section. FEMs of the inboard and outboard fins have been modified by the Model Updating Technique (MUT). The nonlinear stiffness kn=2.35×109N·mm/rad is obtained from zero-clearance real-life fins by the MUT.To reduce the computational burden in numerical experiments,the model reduction method2,34,35is utilized to reduce the DOFs of the folding fin structure. As shown in Fig. 5, the Uz-DOF of the two measure points and the exciting point are reserved. Besides, the Rx-DOF of four hinge points (marked in red boxes) and six modal DOFs are also reserved. Then two nonlinear springs are added to the hinge points of the reduction model with kn=2.35×109N·mm/rad, and the freeplay parameters δ will be specified in specific numerical examples. Finally, the large mass method36and the four-order Runge-Kutta method are employed to calculate the dynamical response of the sinesweep excitation. The time step is 6.25×10-4s, the sweep velocity is 0.1 Hz per second,and the sweeping scope is 30 Hz to 50 Hz.

3.1. Verification of sine-sweep backbone curve extracting method

In this section, we mainly verify the extracting method of fitting points of BCs. The sine-sweep numerical experiments under various base excitations are conducted. The clearance parameter δ is set as 0.003 rad. Fig. 6 is the sine-sweep timedomain displacement responses under 0.60g base acceleration excitation, where the upper and lower plots are the displacement responses of top-left measure point Xtl(t ) and lowerright measure point Xlr(t ), respectively. It can be seen that the amplitude jump occurs after reaching the first-order main resonance, which is a typical phenomenon of nonlinear systems.37,38The Adaptive Chirp Mode Pursuit (ACMP)39method is utilized to extract the amplitude-frequency curves of the first-order harmonic from the measured displacement response data. Fig. 7 shows extracted amplitude-frequency results of the two measure points under different levels of excitation.Note that the resonance peak values all fall on the BCs calculated by Eq.(8). Therefore, the amplitude-frequency points of resonance peaks can be used as fitting points to conduct the BC fitting.

The above results confirm that the fitting points of BCs can be extracted from the sine-sweep displacement data. Actually,the velocity and acceleration data of sine-sweep tests can also be used to extract the fitting points. First, the ACMP method is utilized to extract the amplitude-frequency curves of the first-order harmonic from the velocity and acceleration data.Then, the displacement amplitude-frequency relation can be obtained through the following transformation:

Table 2 lists the estimated clearance and stiffness parameters by the proposed BC fitting framework. As can be seen,although the fitting points come from different response data,the estimated errors of clearance parameter δ are all smaller than 1%and the estimated errors of stiffness knare all smaller than 2 %, which demonstrates the feasibility of the proposed identification framework by the BC fitting.Note that the entire extracting process of fitting points does not require the exciting force data and the response data of nonlinear-related DOFs,which means that the proposed method is an output-only and indirect identification method. Therefore, compared with most existing methods that have to measure the input exciting force and the displacement responses of nonlinear-related DOFs to identify the parametric model of the freeplay nonlinearity, such as FSM, TNSI and CRP methods, the presented method is more practical and useful for engineering problems.

Table 1 Fitting points of BCs from different types of response data by ACMP method.

Table 2 Estimated clearance and stiffness parameters by the proposed BC fitting framework.

3.2. Verification of noise robustness

Noise robustness is a significant evaluation index of identification methods. In this section, we will demonstrate the noise robustness performance of the proposed identification framework. The testing data come from the acceleration signals of Section 3.1. First, different levels of white noises are added into the acceleration data, and the noises are respectively 0.1N(0,1)g, 0.2N(0,1)g and 0.3N(0,1)g, where N(0,1)denotes the standard normal distribution. Then the ACMP method is employed to extract the amplitude-frequency curves of the first-order harmonic from the noised acceleration data.Finally, the fitting points are obtained as the amplitudefrequency points of resonance peaks. Table 3 shows the extracted fitting points,and as can be seen,there are very small differences among different noise levels. These results are not surprising because resonance peaks are usually very large and are not easily influenced by noises.

Table 4 shows the estimated clearance and stiffness parameters from the fitting points listed in Table 3.It can be seen that the estimated errors of clearance parameter δ are all smaller than 1.2%and the estimated errors of stiffness knare all smaller than 0.5 %. Therefore, it can be concluded that the pro-posed identification framework has good noise robustness even involving strong noise, for instance, 0.3 N(0,1)g.

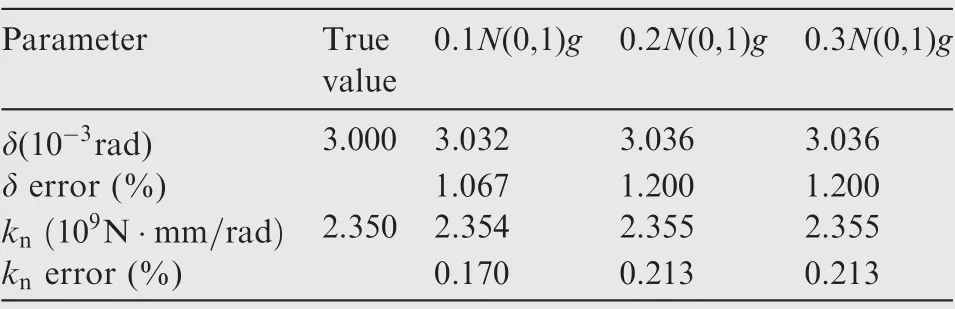
Table 4 Estimated clearance and stiffness parameters from different noised acceleration data.

3.3. Verification by various clearance values

Table 3 Extracted fitting points of BCs from different noised acceleration data by ACMP method.

Table 5 Extracted fitting points of BCs from acceleration data by ACMP method.

4. Application of the proposed framework to real-life folding fin structure

In this section,the parametric model of a real-life folding fin is identified according to the procedures shown in Fig.4.Firstly,FEMs of the linear inboard and outboard fins are established,and the model updating technique is used to obtain a more accurate model. Then the sine-sweep test of the full fin is performed, and the fitting points of BCs are extracted. Next, Eq.(8)is used to fit the sine-sweep results to identify the nonlinear parameters δ and kn. At the end of this section, the identified full fin model is verified by setting clearance as zero and then compared with a zero-clearance real-life folding fin.

4.1. Identification of the linear model of inboard and outboard fins

To obtain the parameters M and K in Eq.(8), the FEM is utilized.First, the linear free modal test is performed on the outboard and inboard fins, respectively. Fig. 8 shows the freeboundary experiment setup of the outboard fin and the inboard fin and their corresponding Finite Element(FE)models.Then the first four flexural modal frequencies are extracted from the frequency response data of the hammer test. Table 7 lists the experiment and FEM results of the first four flexural modal frequencies. As can be seen, the relative errors are all at a very low level, which shows that the values of M and K based on FEM are accurate under free-boundary condition.If the relative error is not at a very low level,the model updating technique should be employed to reduce it.

After obtaining the free-boundary FE model of the inboard and outboard fins, the fixed-boundary condition of the inboard fin is to be taken into account. Fig. 9 shows the fixed-boundary experiment setup of the inboard fin and its corresponding FE model. The fixed screw of the inboard fin is modeled as a mass point,and the other nodes of the fixed surface are connected to it by the multiple point constraints.Then six DOFs of this mass point are fixed. Table 8 lists the fixedboundary experiment and FEM results of the first four flexural modal frequencies of the inboard and their corresponding relative errors.As can be seen,the relative errors are all at a very low level, indicating that the fixture reaches nearly ideal fixedboundary conditions,and the boundary condition is not necessary to be updated.If the relative error is at a high level,given that the free-boundary FE model of the inboard fin has been accurately modeled in the free-boundary test,it can be deduced that the fixed-boundary condition is not ideal and needs to be amended.

Through the aforementioned experiment and modeling, an accurate linear FE model of the full fin is obtained. Then the dimensionality reduction of M and K can be achieved by the model reduction method mentioned in Section 3, which can greatly save computing resources. Up to now, only two unknown parameters knand δ in Eq.(8)are left to be identified.Next, we will show how to identify them through fitting backbone curves.

4.2.Extraction of the fitting points of backbone curves for full fin

To extract the fitting points of BCs, the sine-sweep test is performed on the full fin. Fig. 10 displays the experimental schematic diagram and experiment setup of the sine-sweep test.Using M + P vibration test system to control the sine-sweep test and collect response signals,the accelerations of two measure points are recorded. The sine sweep is carried out from 25 Hz to 50 Hz at the speed of 0.1 Hz per second,and the sampling frequency is 2048 Hz. After obtaining the acceleration signals, the ACMP method is utilized to extract theamplitude-frequency curves of the first-order harmonic for¨X(ω). Then the displacement amplitude-frequency relation can be obtained by Eq. (9).

Table 6 Estimated clearance and stiffness parameters for different clearance cases.

Table 7 Free-boundary modal-frequency results of outboard and inboard fin.

Table 8 Fixed-boundary modal-frequency results of inboard fin.

Fig.11 shows the displacement amplitude-frequency results of the first-order harmonic for the top-left and lower-right measure points under five different levels of base excitation.They exhibit the same jump characteristics with the simulation results shown in Fig. 7, indicating the correctness of the nonlinear restoring force hypothesis in Eq. (1). Then the fitting points of backbone curves can be extracted from the peakvalue point of the amplitude-frequency curves. Table 9 lists the extracted fitting points, and later, the BCs by Eq. (8) can be used to fit them to identify the two restoring force parameters knand δ.

4.3. Identification of nonlinear freeplay parameters (kn and δ)

In this subsection, the final step of the identification framework is carried out. After obtaining the fitting points and the values of M and K, the values of knand δ can be estimated by minimizing Eq.(10)with the values listed in Table 9.Different data combination is employed to estimate the restoring force parameters. Table 10 lists the estimated results of knand δ.As can be seen,the identified results show consistency,especially the clearance parameter δ,indicating the validity of the proposed identification framework. Fig. 12 shows the fitting results of the two backbone curves obtained by employing average values of knand δ. As can be seen, both of them are consistent with the experiment results.

Table 9 Extracted fitting points from displacement amplitude-frequency curves.

Table 10 Estimated parameters of nonlinear freeplay spring.

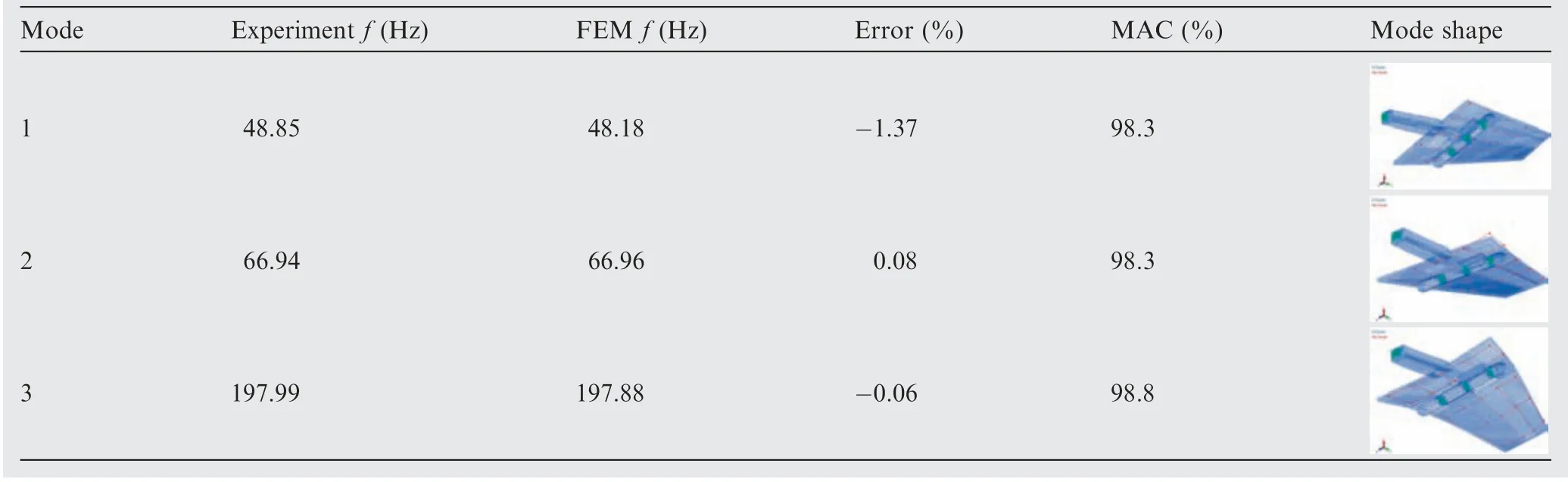
Table 11 Comparison of the modal results of the hammer test of zero-clearance fin and identified fin with δ = 0.

In order to verify the identification precision of stiffness parameter kn, a linear modal test is performed on the full fin with its clearance being sealed off. Then the modal analysis on the full FEM of the folding fin is also proceeding by setting freeplay parameter δ as zero. For the detailed description of the experiment, one can refer to Ref. 2. Table 11 lists the modal results of the experiment and FE model.As can be seen,the errors of modal frequencies are less than 1 Hz for the first three modes of the experiment model and the identified FEM,and meanwhile, their corresponding Modal Assurance Criterion (MAC) values are all greater than 98 %, indicating that the mode shapes are in good consistency.These results confirm the veracity of the estimated stiffness parameter kn.

5. Conclusions

This paper presents a backbone-curve-based framework for the identification of folding fin structures with symmetry freeplay nonlinearities.The strategy proposed here has great practical values in engineering applications, especially when the DOFs with nonlinearity are not easy to measure directly. The experiment results of a real-life folding fin structure support the validity of the presented method. The main conclusions are drawn as follows:

(1) A novel approximate scheme is employed to obtain the explicit expression of the backbone curves of the folding fin structure, and it is demonstrated that the fitting points of backbone curves can be extracted from the sine-sweep data for strongly damped collision systems.

(2) In contrast to other parametric identification methods,the approach discussed here has no compulsive requirement on the measuring responses of nonlinear related DOFs. Using the backbone curve to establish the relation between the measurable DOFs and the nonlinear parameters, we transform the nonlinear identification as a fitting problem of the backbone curves of the measurable DOFs.

(3) The proposed method is an output-only identification framework. Because the backbone curve is excitation independent,there is no need to measure input force signals when using it,and this reduces the difficulty of data acquisition and processing.

(4) A series of numerical experiments verify the noise robustness and the identification accuracy of the proposed method. A real-life folding fin structure is also employed to verify the proposed scheme. The estimated freeplay parameter is in good agreement with the manufacturing tolerance.In addition, when ignoring the freeplay, both the mode frequency and the mode shape of the identified model are in good agreement with the linear experimental folding fin.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors acknowledge the financial supports from the Fundamental Research Funds for the Central Universities, China(No.HIT.NSRIF.2020014)and the National Natural Science Foundation of China (No. 12102103).