Energy-optimal trajectory planning for solar-powered aircraft using soft actor-critic

Wenjun NI, Ying BI, Di WU, Xioping MA

a Institute of Engineering Thermophysics, Chinese Academy of Sciences, Beijing 100190, China

b University of Chinese Academy of Sciences, Beijing 100049, China

KEYWORDS Flight strategy;Guidance and control;Reinforcement learning;Solar powered aeroplane;Trajectory generation

Abstract High-Altitude Long-Endurance (HALE) solar-powered Unmanned Aircraft Vehicles(UAVs) can utilize solar energy as power source and maintain extremely long cruise endurance,which has attracted extensive attentions from researchers. Trajectory optimization is a promising way to achieve superior flight time because of the finite solar energy absorbed in a day.In this work,a method of trajectory optimization and guidance for HALE solar-powered aircraft based on a Reinforcement Learning(RL)framework is introduced.According to flight and environment information, a neural network controller outputs commands of thrust, attack angle, and bank angle to realize an autonomous flight based on energy maximization. The validity of the proposed method was evaluated in a 5-km radius area in simulation,and results have shown that after one day-night cycle,the battery energy of the RL-controller was improved by 31%and 17%compared with those of a Steady-State (SS) strategy with a constant speed and a constant altitude and a kind of statemachine strategy, respectively. In addition, results of an uninterrupted flight test have shown that the endurance of the RL controller was longer than those of the control cases.

1. Introduction

High-Altitude Long-Endurance (HALE) solar-powered Unmanned Aerial Vehicles(UAVs)rely on inexhaustible solar energy to stay in close space for days or longer to perform tasks such as communication relays, network services, surveillance, and reconnaissance.1,2Compared with satellites and stratospheric balloons, HALE aircraft are less expensive and more controllable. However, constrained by the efficiency of battery pack and photovoltaic cells, aircraft platforms are growing in size to satisfy the need for more payloads. Therefore, finding a potential way to help solar-powered aircraft make full use of the sun’s energy has attracted the attentions of many researchers.In addition to improvement on the design methods of HALE,3,4trajectory optimization and energy management strategy have become promising methods.

Based on the law of cosines, the power absorption of solar energy is affected by the incident angle of sunlight,so an optimized flight attitude can be adopted to receive more energy.Klesh and Kabamba might have been the first to study the optimization problem of a solar flight path between two path points, and proposed the dimensionless parameter of power ratio to evaluate the optimal path.5Edwards et al.investigated how to maximize the net power input from solar energy by varying the bank angle or, equivalently, the orbital radius.6Dwivedi et al. sought to maximize the solar power input by solving the optimal bank angle and attack angle in advance.Then the optimized result was used as the desired attitude input for an inner-loop controller, combined with a control methodology based on a sliding mode to validate the effect on a real aircraft.7Nevertheless,they only considered the path optimization problem in a two-dimensional surface. Spangelo and Gilbert explored path planning of a solar-powered aircraft in a three-dimensional space and evaluated the influence of longitudinal motion on energy absorption.8Huang et al.modified the effect of the bank angle in solar energy absorption on the basis of Spangelo’s work,but did not take this as an additional optimization variable.9Both of them fixed the aircraft’s spatial position on a vertical cylinder surface, which in effect distorted the three-dimensional space into a two-dimensional surface and ignored more paths inside the cylinder.

Another possible approach is to explore different Energy Management Strategies(EMS)that make the most use of gravitational potential energy.Gao et al.set the charging power of battery pack as the criterion to supply excess solar-absorbing power to the propulsion system for elevation and to save energy by releasing the gravitational potential energy at night.10Wang et al. proposed a hybrid algorithm combining Gauss Pseudo-Spectral algorithm and Ant Colony algorithm to search the optimal mission path, and employed their combined optimization scheme to achieve continuous flight and improve flight mission capability.11

Trajectory optimization of HALE solar-powered UAVs is a comprehensive problem involving atmospheric environment,flight attitude, and flight mission constraints, which jointly determine the formulation of a flight strategy.The uncertainty of the environment and the constraints of the mission will have a real time impact on the flight trajectory. Hence, methods based on online-optimization are more suitable to solve this kind of problem. Wu et al. studied trajectory optimization of single- and multi-aircraft solar-powered UAVs in movingtarget tracking tasks and verified the effectiveness of their proposed algorithm.12,13Martin et al.used the method of nonlinear Model Predictive Control (MPC) with a receding horizon to maximize the total energy of HALE aircraft for keeping station.14However,MPC-based approaches have two drawbacks:(A) the controller can only decide a flight strategy depending on a limited horizon, and (B) the real-time performance of the controller is reduced due to the iterative solver used in the rolling optimization process.15

Recently, Reinforcement Learning (RL) receives lots of attentions in the aeronautic community due to its real-time end-to-end control performance and adaptability. Relying on a deep neural network, it can generate control strategies that deal with high-dimensional, heterogeneous inputs and optimize long-term goals,16,17which map information to action control instructions and complete the training process of a controller offline. The forward reasoning process of a welltrained neural network with a rapid response can reduce the computational cost and adjust real-time commands for navigation, guidance, and control according to the state,18which frees up more computing power for UAVs’ other tasks, such as reconnaissance task information processing and communication relay task assignment. These characteristics can further enhance the autonomous flight ability of HALE aircrafts.Deep reinforcement learning has been studied in the control of a quadrotor,19,20a small unmanned helicopter,21and a fixed-wing aircraft.22At the same time, application of simulation and real validation on path planning of gliders and stratospheric balloons have shown good results. Reddy et al.used a reinforcement learning model-free framework to explore the problem of unpowered gliders tracking updrafts.23A glider’s multidimensional state and environment information is used as the input to the controller and determines the desired attitude angle at the next moment. Bellemare et al. designed a decision controller using reinforcement learning to determine the movement of stratospheric balloons with the help of a wind field to ensure that the task requirements of the stagnation point can be satisfied.24The above studies have shown that it is a potential way to integrate trajectory optimization and guidance control of an HALE aircraft through its end-to-end characteristics. However, there have been few studies on this problem.

Based on the above deficiencies,present work offers the following contributions:

(1) Reinforcement learning with a continuous action space is employed to solve the energy-optimal three-dimensional trajectory planning problem for HALE aircraft, and a complete training framework of a guidance controller is established.

(2) A trained neural network controller is able to output instructions of thrust, attack angle, and bank angle according to the information of aircraft and environment, which transforms the problem of online trajectory navigation and guidance into an end-to-end way.

(3) Compared to a two-dimensional Steady-State (SS) case and a three-dimensional state-machine case,simulation results in present work have shown 31% and 17% increments of the total stored energy over a 24-hour flight, respectively, which leads to an additional 110% flight endurance in a sustained flight.

The remaining part of the paper proceeds as follows. The simulation environment of the reinforcement learning framework is described in Section 2. The configuration of a soft actor-critic algorithm and key design decisions are presented in Section 3. Then in Section 4, level-flight and statemachine cases are described, and a training process is presented on this basis. The controller is evaluated in light of 24-hour flight and sustained flight cases in Section 5.Finally, Section 6 presents final comments and suggestions for further work.

2. Models

In a flight process, a solar-powered aircraft can use photovoltaic cells equipped on the airfoil surfaces to convert solar radiation into electricity, which is fed to the propulsion system by an energy-management computer or stored in batteries. A schematic diagram of the relationships between aircraft subsystems is illustrated in Fig. 125. This section will introduce the models employed throughout this work, including a dynamics and kinematics model, a solar radiation model,an energy absorption model, and an energy consumption model.

2.1. Dynamics and kinematics model

For solar-powered aircraft trajectory optimization, more attentions should be paid to the optimization process. Therefore, a simplified mass point model is adopted in this work reasonably.

Assuming that the aircraft is not affected by sideslip or the installation angle of the propulsion system,the coordinate system in a no-wind flight of the aircraft is represented in Fig. 2,where OgXgYgZgis the North-East-Down inertial coordinate frame and ObXbYbZbis the aircraft body coordinate system that points from the center of mass to forward, right wing,and down, respectively.

By analyzing forces acting on the aircraft, dynamics and kinematics equations can be developed by the following differential form equations,and detailed derivation can be found in Nayler’s work26:

where V is the flight velocity,while α the attack angle measured between the ObXbaxis and the velocity vector. γ is the flight path angle,and ψ the yawing angle that is equal to the heading angle because of no sideslip.φ is the bank angle,m the mass of the aircraft,and g the acceleration of gravity.x,y,z are the relative positions of the aircraft in the inertial coordinate frame,and the distance to the central point R can be calculated by

Another Euler angle,the pitch angle θ,can be computed by the following equation:

During a flight, the aircraft is subjected to the following forces:Gravity,the aerodynamic lift force L,the aerodynamic drag force D,and the thrust T generated by the propelling system.Their directions are shown in Fig.2 as follows:The thrust is parallel to the ObXbaxis,the lift force is perpendicular to the velocity,and the drag force is parallel to the negative direction of the velocity. The lift force L and drag force D can be denoted by

where ρ is the density of air calculated according to the 1976 US Standard Atmospheric Model27. CLand CDare the lift and drag coefficients, respectively. S is the wing area. In this work, CLand CDare fitted to a set of equations of the Reynolds number Re and the attack angle α, where the Reynolds number is calculated according to current altitude and flight velocity. The fitted results are represented for facilitating the simulation in the following forms:

where the values of Aijand Bijare listed in Tables 1 and 2,respectively.

2.2. Solar radiation model

In order to estimate the solar radiation at the position of the aircraft in real time,a mathematical model proposed by Duffie and Beckman28and Wu et al.29is introduced.

In Fig.3,npmis the external normal unit vector of the photovoltaic plane,and nsthe vector that points from the center ofthe photovoltaic cell to the sun. αsis the solar altitude angle,and γsthe solar azimuth angle, which can be determined by the local latitude φlat, the solar declination δs, and the solar time θh, as denoted in the following equations:

Table 1 Values of Aij.

where φstis the central longitude of the local time zone, and Hctis the local clock time.

Due to the thin clouds and reduction in impurity particles in the upper atmosphere,the calculation of the solar radiation can ignore the contribution of the solar reflection radiation.11The total solar radiation Isolaris the sum of the direct radiation Idirand the scattered radiation Idiffas

in which the extra atmospheric solar radiation Ionand αdepare given by

where Gscis the standard solar radiation 1367 W/m2, Rearthis the mean radius of the earth 6357 km, and h is the altitude.

2.3. Energy absorption model

The solar flux through the aircraft photovoltaic cells, which would be converted into electric energy, can be calculated based on the geometric relationship between the normal vector of the photovoltaic cell plane and the incident vector of sunlight.

where the installation angles of the solar panels are ignored.The shorthands cα and sα represent cos(α) and sin(α) for the sake of simplicity.Then the total input solar energy power Pso-larconverted from the solar flux is

2.4. Energy consumption model

The HALE solar-powered aircraft mostly adopts an electrically-propelled propeller system, which generates thrust to resist drag. In addition, during the flight process, it also needs to maintain the necessary avionics systems working stably. In the work, a simplified propulsion system model and constant avionics power are taken to calculate the required power Pneed30as

where Paccdenotes the power of avionics,Ppropis the power of the propulsion system, ηpropis the efficiency of the propeller,and ηmotis the efficiency of the motor.

2.5. Energy storage model

The battery pack on the HALE aircraft can either power all the systems or store excess solar energy for use at night. In recent years, lithium batteries have been widely used in solar-powered aircraft due to the advantages of high specific energy and stable charge-discharge process.

The State of Charge (SOC) is used to estimate the remaining available energy in a battery compared to that of the fullycharged,and the rate of change of the SOC is related to the net power of the battery Pbatteryas

where Ebatteryis the current energy in the battery pack, and Ebattery,maxis the maximum energy capacity of the battery.For battery charging, Pbatteryis positive when the energy consumed in a flight is less than the energy converted by the photovoltaic cells, while it is negative on the contrary. When the battery is fully charged, Pbattery=0.

In addition to the energy in the battery,the HALE aircraft can store the gravitational potential energy Epotentialthrough elevation that can be released by gliding down to maintain the airspeed required for a flight at night. In this work, the gravitational potential energy relative to the initial height h0is considered only for purposes of the net energy expression as follows:

In summary, through the establishments of the above five mathematical models, the state of the aircraft can be solved in real time through a numerical solution method in the simulation process, which provides a detailed description of the environment part of the reinforcement learning framework for the aircraft trajectory optimization problem. Detailed parameters and physical constraints of the studied HALE solar-powered aircraft are listed in Tables 3 and 4,respectively.

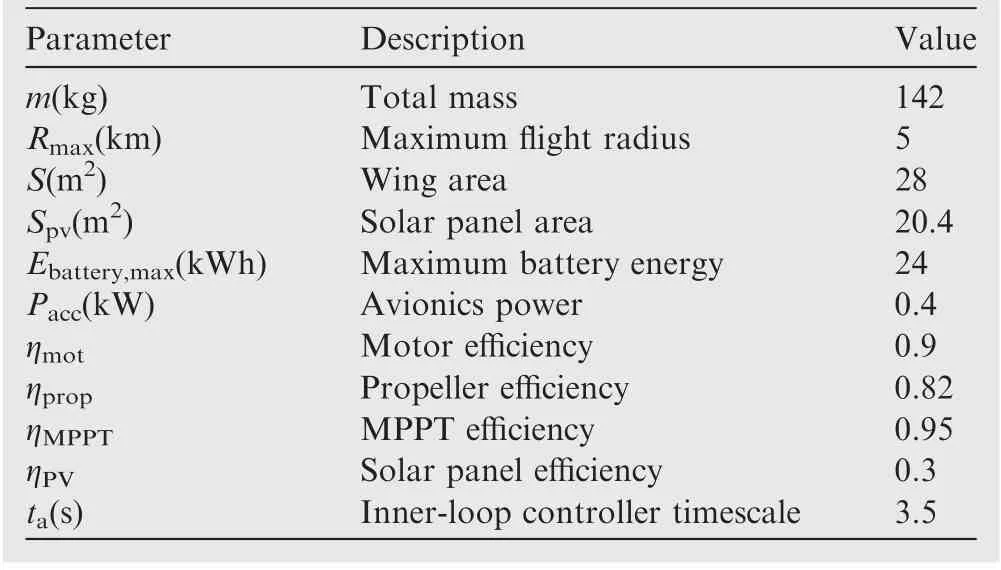
Table 3 Basic parameters of the studied aircraft.

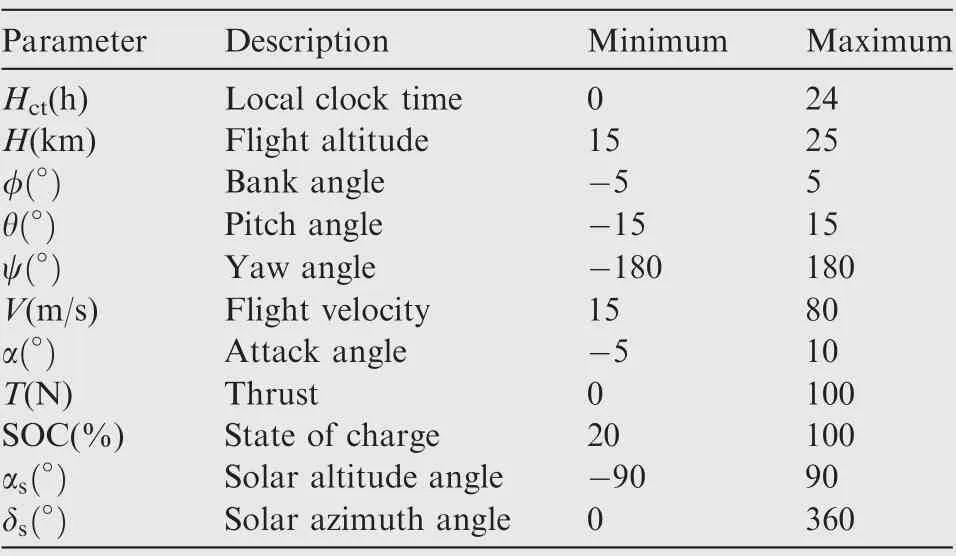
Table 4 Constraints of variables.

3. Reinforcement learning framework

In this section,the reinforcement learning framework for training the HALE solar-powered aircraft guidance controller is introduced in detail, including the soft actor-critic algorithm,state space setting, action space, and an energy-based reward function.

3.1. Soft actor-critic algorithm

The Soft Actor-Critic (SAC) algorithm belongs to methods of model-free reinforcement learning proposed by Haarnoja et al.and is an off-policy solution that bridges the gap between stochastic strategy optimization and deterministic strategy gradient algorithms.27Unlike many alternatives, SAC is considered relatively insensitive to its hyperparameters, which makes it an ideal choice for current modeling setup in present work.

In general, the reinforcement learning problem can be defined as an optimization process to find a policy π by maximizing the expected sum of rewards in a Markov Decision Process (MDP), defined by a tuple (s,a,p,r). The state s ∈S,and the action a ∈A,in which S and A are the state and action spaces, respectively. The state transition probability p represents the probability from stto st+1with action at. In the meantime,the environment generates a reward r(st,at)on each transition.The optimal policy π*is the one that can achieve the maximum expected total rewards and is defined as

where, γ is the factor that discounts the value of future rewards. In the SAC algorithm, a central feature is entropy regularization, that is, the agent gets a bonus reward proportional to the entropy of the policy at each transition. Therefore, the process for finding the optimal policy π*can be rewritten as

where Π is the feasible sets of the policy function,and Zπold(st)is the partition function that normalizes the distribution and does not contribute to the gradient with respect to the new policy. Repeated applications of soft policy evaluation and soft policy improvement will converge to the optimal maximum entropy policy among the policies in Π.32

In this work, SAC concurrently learns a policy πθneural network that takes responsibility to map states to actions,and two Q-functions Qφ1, Qφ2neural networks that take charge of estimating values of state-action pairs. Similar to the deep Q-learning algorithm, the performance measure of the Deep Neural Network (DNN) is defined as the Mean Squared Error (MSE) between the Q-evaluated value and the Q-target value. Let (s′,a′) represent the tuple at t+1, and the loss functions for the Q-networks are

The policy is optimized according to

where α is the temperature parameter that balances the gap between the policy entropy and the reward, which can be a fixed or adaptive value. H is the entropy of the policy and can be represented as

The algorithm pseudocode is shown in Algorithm 1.

Algorithm 1: Soft actor-critic34 Initial policy parameters θ, Q-function parameters φ1,φ2 Initial replay buffer D Set target parameters φtarg,1 ←φ1,φtarg,2 ←φ2 For episode=1 to M do:Observe state s and select action a ～π(·|s )Execute a in the environment Observe next state s′, reward r, and done signal d to indicate whether s′ is terminal Store (s,a,r,s′) in replay buffer D If s′ is terminal, reset the environment state.If it’s time to update then For j=1 to N do:Randomly sample a batch of transitions B = s,a,r,s′( ){ }from D Compute the target for the Q-functions:y(r,s′)=r+γ mini=1,2 Qtarg,i(s′,a～′)-αlogπθ(a～′|s′),a～′ ～πθ ·|s′( )Update the Q-functions by one step of gradient descent using2∇φi 1B||∑s∈B min i=1,2 Qφi(s,a～θ(s))-y(r,s′)for i=1,2 Update target networks with φtarg,i ←τφtarg,i+(1-τ)φi for i=1,2 End for End if End for

3.2. State space

To fully represent various information of the system, the aircraft’s position, flight attitude, flight velocity, local time, battery state, and action information are used as the inputs of the reinforcement learning controller. For purpose of better adaptation to the environment, the solar altitude and azimuth angles are employed to replace the clock time information.Therefore, at timestep t, the state can be represented as a vector, i.e.,

It is well-known that in ODE processing methods, the shorter the simulation step size is, the more accurately the flight state will be solved. However, the calculation time will increase at the same time.For exploring a flight strategy under a large space-time span, and considering the slow dynamic characteristics of a high-altitude solar-powered aircraft, the state of the aircraft is observed once every n simulation steps,and the corresponding guidance commands are computed,which will be maintained in the skipped simulation steps.

In order to accelerate the convergence rate of the neural networks, each state component is normalized using linear rescaling35to eliminate the difference between their quantity units as

To make the feedforward policy network realized dynamic characteristics of the system, the input vector of the reinforcement learning controller at each timestep includes some previous observation information.For example,the neural network input at time t is a one-dimensional vector composed of st,st-1,and st-2.

3.3. Action space

For a high-altitude long-endurance aircraft, a guidance controller can not only ensure a stable flight of the aircraft, but also fully consider the longer time to meet mission requirements. According to the energy absorption model, it can be known that the control variables are naturally selected as the pitch and roll angles. However, since the stability of the solar-powered aircraft is greatly affected by the pitch angle,its climbing process can be determined by the thrust and the angle of attack.

In this work, the action space of the controller is threedimensional, consisting of the commanded increment thrust ΔTcmd, the attack angle Δαcmd, and the bank angle Δφcmd.Under the condition of not exceeding the physical limit, the controller can choose any continuous value in the set range listed in Table 5.

To focus on the generation of guidance commands,an ideal inner-loop controller is selected to simplify the problem:For a given command Δucmd,a proportional feedback control mechanism at a user-set timescale tais adopted as follows:

where udesiredis the desired values of T,α,φ , and u0is their states at the timestep of an output action.

3.4. Reward

The success of an RL experiment deeply depends on the design of a reward function. In the research field of trajectory optimization for solar-powered aircraft, the aim is essentially to maximize the available energy after one day-night flight circle,which can only be obtained after the completion of an episode,and sparse rewards make training difficult. Therefore, a kind of dense reward function is designed in this work,which guides the agent toward the purpose of maximizing the utilization of solar energy.

The reward function consists of three types, each of which encourages the RL controller to pursue an abstract goal.When the sun is just rising, the aircraft should be fully charged by solar power adoption until it meets certain SOC condition.Note that 95%SOC is chosen as the critical value to take into account the damage of battery charge and discharge.Then the aircraft should convert the excess solar energy into gravitational potential energy. Finally, the aircraft should maintain as much battery energy as possible after sunset to supportthe flight before sunrise on the next day. According to the above ideas, a reward function without constraints about the clock time information is expressed in the following form:

Table 5 Values for change of each command.

where the coefficient of the potential energy term is to magnify its effect to the same level as that of the battery energy.

In reinforcement learning,the controller gradually achieves the desired goal by continuously exploring the environment.Therefore, in order to simulate a more realistic flight environment,the aircraft is considered to have crashed and this simulation episode ends at once when any component of state in Table 4 goes out of range. Then a new episode restarts at the initial state. The total reward per episode will be reduced due to early termination, and therefore these situations will be gradually avoided as the training progresses for more rewards.

4. Simulation setting

In this work,the task area used for the test is assumed to be a cylinder with a radius of 5 km,located at(39.92°N,116.42°E).The basic parameters and constraints of the aircraft are kept consistent with those in Tables 3 and 4.

4.1. Solar data verification

In order to verify the correctness of the program, the corresponding angles calculated by PySolar36are taken as a control case. Fig. 5 shows the solar altitude and azimuth angles at a 15 km altitude for the summer solstice at (39.92°N,116.42°E). Due to the differences in calculation models, there is an almost constant time offset between the two results,which is about 1.7% relative to 24 hours, and the duration of sunshine is not affected.Fig.6 illustrates the curves of solar radiation in four seasons at a 20 km altitude generated by the adopted model.At the same time,the curve of Martin’s work14calculated for the summer solstice at 35° N is quoted as comparison,which shows that the relative error between programing in present work and Martin’s result is within 2%. The above results verify that the solar radiation model adopted in this work can meet the requirements.

Fig.7 displays the variations of solar radiation over time at different altitudes at (39.92°N, 116.42°E) during the summer solstice.It can be seen that with the elevation,the time of sunlight gradually increases and then stops changing above 15 km,which is the reason why we set the minimum limit of altitude as this. In the meantime, the total solar radiation increases with elevation. However, during the flight of the high-altitude long-endurance aircraft, the Reynolds number and air density decrease with an increase of the altitude, so the flight speed needs to be increased to maintain a lift force against the gravity.At the same time,the air drag also increases.According to the dynamical models in Section 2, it can be seen that the power consumed gradually increases with the elevation of flight.

4.2. Steady-state initialization and benchmark case

For evaluating the performance of the RL guidance controller,a steady-state circular case and a kind of state-machine case are established in this section.The steady-state case is an optimal two-dimensional circular trajectory that maintains a constant velocity and a constant altitude, while the state-machine case is a widely studied way to consider the influence of gravitational potential energy on the total energy, both of which have been used as control cases in the literature10-13to compare the change in an aircraft’s total stored energy. In present work, the methodology in Martin’s14work is adopted to find these two strategies.

Therefore, a steady-state circular case at a random altitude is introduced using the following optimization method:

By solving the above optimization problem, the balancing conditions of a constant-radius orbit at each height can be obtained. Based on the analysis in Section 4.1, it is reasonable to set the steady-state flight altitude as 15 km that is the minimum height of the mission area, because it requires the least power. Using the optimization package of Python SciPy,parameter values of this case can be obtained, as shown in Table 6, and will be used as the initial condition for training the reinforcement learning controller.Under this initial condition, a steady-state three-dimensional trajectory diagram can be obtained that is illustrated in Fig. 8(a).

In addition to the constant velocity and altitude case, a widely-studied state-machine case is also used for comparison.In essence, an aircraft that adopts this strategy flies along the outer surface of a cylinder, while transformation operations of climbing,cruising,and descending are carried out according to certain preset rules. Typical rules are as follows:

(1)Maintain level flight with minimum consumption power at the minimum altitude until a certain SOC is reached.

(2) Perform spiral ascending until an appropriate limit height is reached.

(3)Hover at the maximum limit altitude with the minimum power until the battery can’t stay at a full state.

(4) Descend down to the minimum altitude limit.

(5) Cruise at the minimum restricted altitude.

Following the above rules, the commands input for each stage is obtained by interpolating between the minimum power state inputs at different heights.Then for comparing to the RL controller,the certain SOC for a changing stage is set as 95%,and the maximum height is set to the maximum altitude that the RL has reached. The path angle of the climbing state isset as the average value of the climbing path angle of the RL controller.The path angle of the descent is searched by the grid method to obtain the critical zero-power angle. The trajectory generated by the state machine is displayed in Fig. 8(b).

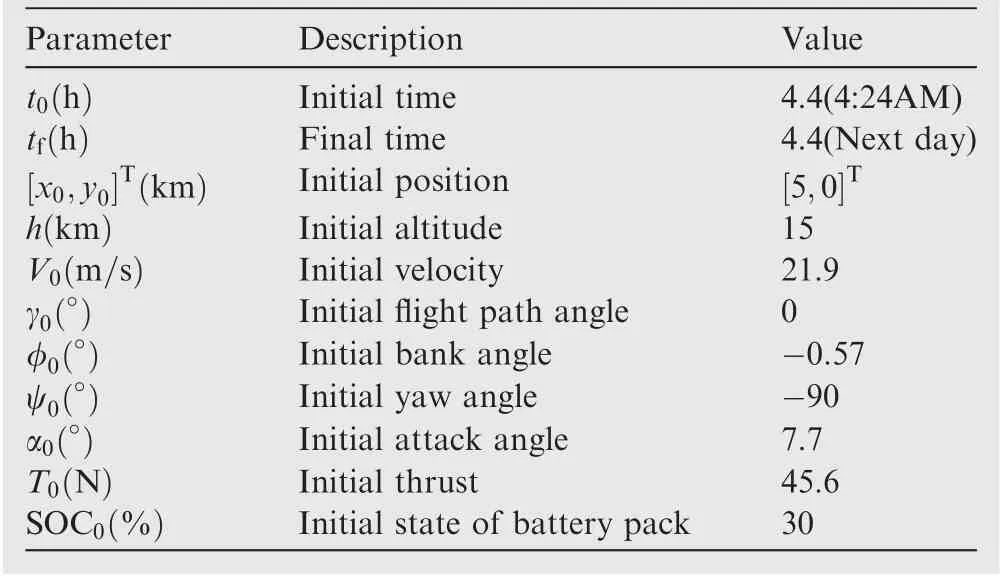
Table 6 Initial condition settings for a steady-state case.

4.3. Network and hyperparameters setting

The network architecture adopted is shown in Fig.4,and there are three parts of the whole framework:

(1)The policy network is a probability density function estimator that predicts the distribution of actions conditional on the state. The policy network consists of two fully-connected hidden layers of 512 units, each of which is followed by a ReLU activation function.In our design,the policy is assumed to be a Gaussian distribution. Therefore, the last layer of the policy network consists of two parallel linear layers that encode the mean and standard deviation for every command type, respectively.

(2)Two Q-value networks are employed to estimate Q(s,a).Both of them have two fully-connected hidden layers of 512 units, each of which is followed by a ReLU activation function. Then their last layers output one Q-value each.

(3) To speed up training, the target Q-value networks are set with the same architectures as those of Q-value networks and are updated by soft ways.

The training process is implemented by Tianshou Platform.37In all of the experiments, hyperparameters are consistent with those of Haarnoja et al.33.The learning rates of both policy and value networks are set to 3×10-4and using Adam optimizer.38The number of samples per minibatch is 256.The temperature parameter (α) of the SAC algorithm and the reward discount value (γ) are consistently set to 0.2 and 0.99, respectively. The capacity of the replay buffer is generously set to include 1 million samples. The target smoothing coefficient (τ) is set to 0.005.

The flight information is updated with a simulation step size of 0.02 s. The controller observes the current state every 20 s and forms a vector with the previous two observation states then inputs it to the policy network to get the commands. Therefore, the maximum number of time steps in an episode is set to 4320.

The test episode runs once every training 0.01 million timesteps, and the flight simulation timesteps and the total reward of that episode are visualized. Fig. 9 shows the curves of the training process with 5 different random number seeds. After 5 million timesteps, the controller can converge and achieve long-term flight. The trained policy network is deployed on a laptop with an i5-10210U CPU,then the average of a hundred timesteps is taken, and each reasoning process spends about 1 ms.

5. Results

5.1. 24-hour flight

A trained RL controller was employed to guide a 24-hour flight of the solar-powered aircraft. The trajectory generated by the RL controller is displayed in Fig. 10. The altitude and SOC curves of the whole process are illustrated in Fig. 11.The time histories of the flight state that includes thrust,velocity, path angle, attack angle, bank angle, and pitch angle are shown in Fig. 12. The whole day power information is illustrated in Fig.13.For better analyzing the trend of flight information over the 24-hour span, some curves were processed using OriginePro (Learning Edition) internal smoothing tool:light color lines are true values and dark lines are smoothed by moving averages with a window size of 70 in Figs. 12 and 13.Note that the time on the abscissa is counted from the initial condition (4):24 AM at local clock time and represents the flight endurance. It can be clearly observed that the strategy of the RL controller is mainly divided into five stages: charging, climbing, high-altitude cruising, descent, and lowaltitude circling.

5.1.1. Stage 1: charging

The aircraft started level flight around the minimum altitude since 4:24 AM that was also the time when the sun rose. The aircraft was kept at an altitude of around 15 km for about 5.3 hours to ensure the lowest energy consumption.

As can be seen from Fig. 13(c), the charging power of the battery was negative before 5:42 AM, which means that the solar energy and batteries together powered the system, and Pbatterygradually increased with an increase of the solar altitude angle. The battery SOC dropped to the lowest state of 24% at 5:54 AM and began to improve.

In Fig.12,the thrust force was basically maintained around 42 N, and both of the attack angle and pitch were maintained at 5.6°in average,which means that the path angle at this stage was maintained at 0° during the large time span.

Fig. 14 illustrates the trajectory of two circular periods starting at 6:00 AM in this stage, in which darker points represent the bigger Psolarand the golden arrow points to the sun. The aircraft chose to descend as it flew toward the sun,and to climb slightly as it flew in the opposite direction,which reduced the incident angle between solar radiation and the photovoltaic cells, and the aircraft received more solar power.Similar phenomena have also been found in Martin’s14and Marriott’s39works, which proves that the results of present work are reliable. It can be seen from the scatter diagram of battery power that the energy absorption benefit brought by climbing was greater than the increment of power consumption, so the battery power was positive while the discharge power was reduced by reducing the thrust during sliding.Therefore,the aircraft was more inclined to circle in this stage,which was also the reason for choosing a smaller turning radius in the early stage.6This periodic motion was also responsible for the oscillations of other state components in Figs. 12 and 13.

In this stage, the battery of the aircraft was charged from the initial 30% SOC to 60% SOC, storing 7.2 kWh energy in the battery.

5.1.2. Stage 2: climbing

When the solar power was sufficient, the aircraft started to climb from the lowest altitude. As can be seen in Fig. 11, the aircraft was already ready to climb at 60% SOC, while in the reward function, the critical battery condition was set to Fig.13 Comparison of power information generated by RL,SS,and SM in different stages.get 95% SOC before adding a potential energy term, which proved that the RL controller could be aware of preparing for better returns in advance.

From Fig.12,the thrust at this stage immediately increased to the maximum limit of 100 N. The pitch and attack angles increased synchronously which caused the path angle to change from 0° to 2.2°. Due to the elevation and increment of the velocity, the bank angle gradually increased to -4.4°in order to remain within the effective radius. At an altitude close to 24 km, the thrust started to fluctuate and gradually decreased to avoid exceeding the upper limit of 25 km. In the meantime, both of the pitch and attack angles also decreased to reduce the climbing path angle.

From Figs. 13(b)-13(c), the solar energy absorbed in this stage was used to charge batteries and supplied to power propulsion systems and avionics simultaneously.Since the aircraft spent more power climbing, the battery charging power was less than that of the steady-stage case, and the battery reached the full state at a later time. Compared with the state-machine case, the RL controller entered the climbing stage earlier, and the peak value of the output power was lower.

During the climbing stage, the aircraft was gradually charged 100% SOC at 12:00, and stored 3.48 kWh of gravitational potential energy, which was equivalent to 14.5% of the extra maximum storage capacity of the battery.

5.1.3. Stage 3: high-altitude cruising

When the aircraft reached an altitude of 24 km,its bank angle stayed roughly at -4.3° and increased slightly as it tried to take full advantage of the solar power to climb, as seen in Fig. 12. The angles of attack and pitch gradually leveled off to 7.9°and 7.7°,respectively,which caused a small fluctuation of the climbing path angle for adequate storage of potential energy. The maximum altitude of the flight 24.37 km was reached at 14:40, while the total stored energy reached 27.63 kWh that is 1.15 times the maximum capacity of a battery.

From Fig. 15, the absorbed solar power was 0.18 kW higher than that of the steady-state case on the average in this stage.The reason is that the aircraft cruised at a higher altitude and got more absorbed power from making frequent turns.From Fig.13(c),it can be seen that at 15:30 PM,the absorbed energy power was beginning to fail to sustain the energy needed at high-altitude cruising,so the aircraft gradually changed from a potential energy priority strategy to a battery energy priority strategy.

Fig.16 shows the trajectory of two circular periods starting from 16:30 PM in this stage, in which darker points represent the bigger Psolarand the golden arrow points to the sun.Since the current solar radiation was not sufficient for level cruise at this altitude,the aircraft began to spiral down.In this process,for absorbing more solar energy, it can be obviously seen that the phenomenon was similar to Stage 1: the aircraft glided down when flying towards the sun, and climbed when flying away from the sun, which decreased the angle of incidence as much as possible, so as to increase the absorption power of solar energy.This phenomenon is another strong proof that the RL controller can track solar radiation autonomously.Although reasonable, it is the first time when that phenomenon at sunset has been discovered. However, a higher thrust required for climbing at high altitude resulted in a greater thrust fluctuation than that in Stage 1, which was also the reason for the fluctuation of state components in Figs. 13(b)-13(c).

5.1.4. Stage 4: descent

The aircraft began to descend when the solar power was not enough to keep battery at the fully-charged state on a circular orbit, and the descent path angle gradually increased from 24 km altitude onwards. This process lasted about 5 hours from 16:30 to 21:20.

As the sun neared to set,it can be clearly seen that the craft reduced thrust to zero to achieve a zero-power glide and retain more battery energy, which means that the aircraft was beginning to adopt a battery-first strategy.Compared with the statemachine case,the aircraft tended to gradually reduce the thrust output to maintain the altitude as much as possible to preserve gravitational potential energy, during which time the battery could still be charged to take full advantage of the sun’s power at dusk. The path angle gradually decreased from 0 to -1.8°.Near the minimum altitude, the aircraft gradually recovered from the zero-power glide to the level-flight state.

From Fig. 13(a), it can be seen that the aircraft absorbed more of the solar energy because it was at a higher altitude than that of the steady-state case,and by adopting a glide descend,the battery discharge power got 1.35 kW less than that of the steady state, as seen in Fig. 13(c).

At the end of this stage, the battery was still kept at 90%,and the potential energy was almost 0. The aircraft then utilized that left energy for the rest of its flight.

5.1.5. Stage 5: low-altitude circling

During this stage, the sun was below the horizon completely.In order to save energy,the aircraft chose to cruise at the lowest altitude.

As can be seen from Fig. 12, the state components of this stage were basically the same as those of Stage 1. The thrust was maintained around 42 N, and the bank angle was maintained at -2.6°. However, there was a slight oscillation at the pitch angle of the attack angle at 00:30,which caused a fluctuation of the height,but the aircraft immediately leveled off.

From Fig.13,it can be seen that energy consumption about 1.36 kW maintained for a long time in the second half of the process was similar to those of the steady-state and statemachine cases, which were only 0.01 kW higher because the strategies essentially aim to fly with minimum power.

This stage was kept until the start of the next day’s flight,and Stage 1 started again.

Fig. 17 shows the time histories of the battery SOC and total stored energy (Ebattery+Epotential). In addition, the steady-state and state-machine cases were compared against the trajectory generated by the RL controller. Results imply that a maximum total stored energy of 27.6 kWh was received by the RL controller due to the gravitational potential store,which is 15% higher than the steady-state total stored energy of 24 kWh. After a 24-hour flight, the total stored energy left was 8.76 kWh,which was 21.7%higher than the initial state of 7.2 kWh, 16.8% higher than that of the state-machine 7.5 kWh, and 30.7% higher than that of the steady-state 6.7 kWh. The results strongly suggest that a neural network controller trained by reinforcement learning could automatically plan a flight path and support longer-endurance flights.

5.2. Uninterrupted flight

Previous researchers have generally adopted an optimization method for specific conditions to prove the feasibility of the method, so a re-optimization process under different conditions may lead to a decreased real-time performance. Therefore, it is doubtful whether the optimal solution obtained by one 24 h condition could be used for flight guidance when it is not changed.

To verify the effectiveness in a longer time span, the RL controller trained in Section 3.1 was directly used in a continuous flight test without time limit and modification.The initial conditions of this test were completely consistent with those before, and steady-state and state-machine cases were also introduced as control cases.

Fig. 18 shows the time histories of 59-day flight information, in which the horizontal axis represents the time from 4:24 AM every day,the vertical axis shows the number of days since the summer solstice, and the depth of the color reflects the value of the state component. It can be seen from Fig. 18(d) that the sunrise time was gradually delayed and the sunset time got gradually earlier. Under this trend, the aircraft could automatically adapt to different lighting conditions and gradually postpone the time of climbing and the time of being at a higher altitude, as shown in Fig. 18(a). As can be seen from Fig. 18(b), the SOC of 4:24 AM every day decreased with an increase of the daily ordinal number, which was related to the gradual lengthening of the night flight time.

Fig.19 shows the extreme state information reached by the RL-controlled aircraft in the 59-day flight.As can be seen from Fig.19(a),although the state of a full charge could be reached every day, the time to reach this state was gradually delayed.As can be seen from Fig. 19(b), the minimum SOC was decreasing every day,and the time to reach this state was gradually receding as the sun rose later.It can be seen from Fig.19(c) that the value of the aircraft reaching the highest altitude also decreased, indicating that the controller could independently judge the environment and flight information and adopted an adaptive strategy with the first consideration of battery energy.

Flight profiles on the 2nd,30th,and 50th days were selected for verifying the above trends. As shown in Fig. 20, with an increase of the flight time span, the aircraft would gradually delay the time to climb, while the high-altitude cruise stage at an altitude of more than 24 km would gradually shorten,from 3.2 h on the 1st day to 1.7 h on the 50th day,and it would enter the glide stage earlier.This indicates that the trained controller could dynamically give some flight guidance to the aircraft.

As can be seen from Fig. 21, the RL-controlled aircraft could maintain its own energy well at the initial phase of uninterrupted flight and reached a maximum total energy of 8.78 kWh at 4:24 AM on the 13th day, but the total energy at 4:24 AM per day gradually decreased with a lengthening of the flight time. In the meantime, an aircraft guided by a state-machine or steady-state strategy could not maintain its own energy. The RL-controlled aircraft was able to complete 59 consecutive days of flight, which obtained an improvement of approximately 110% over the 28 days of the state machine and the 27 days of the steady-state strategy. However, the same is that the above three strategically-controlled aircraft in the morning charging stage on the last day of their own flight process due to low battery power was judged to have crashed (Fig. 22).

5.3. Online and real-time performance

In general,HALE UAVs stay in near-space for a long time,so their ability to plan autonomously under disturbance of uncertainty is extremely important.A good controller should be able to respond quickly to certain emergency situations.

Three cases were selected to demonstrate the online performance of the RL controller:(A)in Case 1,during the climbing stage,the aircraft circled for 30 minutes at the current altitude to perform a specific mission;(B)in Case 2,during the descent stage,the aircraft circled for 30 minutes at the current altitude to perform a specific mission; (C) in Case 3, there were no specific missions for the HALE aircraft.At the end of the mission, the trajectory was re-planned.

Table 7 records the mission information and the final SOC after a 24-hour flight of different cases.Fig.21 shows the flight profiles of these cases, from which it can be found clearly that the RL controller could make online flight trajectory planning under uncertainty missions and dynamic environment.

At the same time, a Model Predictive Control (MPC)method implemented in Martin’s work14was employed to predict the trajectory in the next 30 minutes based on the state at the end of the mission. All the optimization parameters were kept as default, and the calculation time is shown in Table 8.The MPC method spent 7.8 minutes getting optimized commands and trajectory, which was on the same order of magnitude as the computational time measured by Marriott et al.39Meanwhile, the well-trained RL controller only spent 2.01 s generating a prediction with a developed environmental model which benefited from the end-to-end control and information mapping ability of the neural network.

Table 8 CPU time of predicting a 30-minute horizon trajectory.

6. Conclusions

In present work, a guidance controller integrated with trajectory planning of solar-powered aircraft using a reinforcement learning framework is introduced in detail.

(1) A complete numerical simulation environment of a high-altitude long-endurance solar-powered aircraft for reinforcement learning was established, including a dynamics and kinematics model,a solar radiation and absorption model,and an energy storage model.

(2)Based on the soft actor-critic algorithm with continuous actions, a reinforcement learning framework containing state and action spaces was designed. According to the objective of maximizing energy, a kind of reward function was introduced. A neural network controller was designed to provide instructions of thrust,attack angle,and bank angle for guiding the aircraft on long endurance.

(3) The RL controller can autonomously learn five stages:charging, climbing, high-altitude cruising, descent, and lowaltitude circling. Moreover, it can satisfy real-time end-toend control requirements.

(4) Simulation results have shown that after one day-night flight,the remaining battery energy of the aircraft with the RL controller received 17%and 31%increments than those of the constant-speed and constant-height strategy and the state machine, respectively. In a continuous-flight simulation test,the flight endurance of the RL controller was improved by 110% compared with those of the constant-speed and constant-height strategy and the state machine.

(5) For uncertain missions and environment, the RL controller can regenerate commands according to current information. Combined with a developed model, it can quickly predict a future trajectory to obtain greater energy.Compared with methods based on Model Predictive Control (MPC), the inference time was greatly reduced to seconds.

The above results in this work have proven the feasibility of reinforcement learning in combining mission objectives with guidance and control for HALE aircraft.

Moreover,as a strategy of solar-powered aircraft with obvious stage characteristics,it is very suitable for setting different strategies by hierarchical reinforcement learning.The influence of a wind field in air on high-altitude long-endurance aircraft is also worth exploring in future work.

Table 7 Settings of the specific mission condition and final SOC.

Acknowledgement

This study was supported by the Foundation of the Special Research Assistant of Chinese Academy of Sciences (No.E0290A0301).