Solar sail attitude control using shape variation of booms
Feng ZHANG, Shengping GONG, Horn GONG, Hexi BAOYIN
a School of Aerospace Engineering, Tsinghua University, Beijing 100084, China
b School of Astronautics, Beihang University, Beijing 100083, China
KEYWORDS Attitude control;Boom deformation;Dynamics;Solar radiation pressure;Solar sail
Abstract Active attitude control of solar sails is required to control the direction of the force generated by Solar Radiation Pressure(SRP).It is desirable to control the attitude through propellantfree means.This paper proposes a new method for attitude control of solar sails:A boom consisting of ‘‘smart” structural material can be deformed by the piezoelectric actuator, and Solar Radiation Pressure torque will be generated due to shape variation of sail membrane caused by boom deformation.The method has the advantages of simple structure,small disturbance and small additional load,and is not limited by the size of the solar sail.The case of rendezvous with the Asteroid 2000 SG344 is used to verify the attitude control around the pitch and yaw axes.
1. Introduction
Using the continuous acceleration provided by the Solar Radiation Pressure, a solar sail is able to gain a large speed after a long time of acceleration, which may be 4-6 times faster than the fastest spacecraft propelled by rockets.1,2Solar sails can also realize some special non-Keplerian orbits that are difficult for traditional spacecraft, such as heliocentric displaced orbits3,4, artificial Lagrange points5-7, H-reversal trajectories8,9, sun-synchronous orbits for geotail10-12, etc. These orbits have their potential applications because of solar sail’s propellant-free characteristic. Japan and the United States have successively carried out in-orbit verification of solar sails.13-15
The magnitude and direction of the Solar Radiation Pressure force are determined by the attitude of the solar sail.Active attitude control is necessary to steer a sail orientation relative to the sunlight as a means to control the orbit. However, a large-area solar sail usually has much larger moment of inertia and Solar Radiation Pressure disturbance torque than that of ordinary spacecraft.A square solar sail with a side length of 40 m produces a sunlight-induced disturbance torque approximately 100 times larger than that of a general geosynchronous communication satellite.16Wie studied the feasibility of the solar sail in the Earth’s orbit using momentum wheels for attitude control. It was found that a huge momentum wheel is needed to offset the interference torque generated by factors such as centroid and center-off offset.17Therefore, it is not suitable to use conventional methods to control the attitude of solar sail and an efficient propellant-free attitude control method is necessary for a solar sail mission.
According to different configurations, the attitude of a solar sail can be controlled by using different methods such as spin stabilization,18-20three-axis attitude control, and passive attitude stabilization.21,22The spin stabilization scheme and the passive attitude control scheme have special requirements on the shape of the solar sail. The spin stabilization method usually requires a larger control torque to change the attitude because of the larger spin angular momentum.Besides,maintaining the spin of the system requires extra control torque for some cases.16The passive attitude control based on the special configuration can only achieve some desirable sun-pointing attitude.23,24The three-axis attitude control can realize accurate attitude control. Most of previous literatures focused on the three-axis attitude control in the field of solar sail attitude control.
A square sail with booms is usually adopted for a three-axis stabilized solar sail.The principle of obtaining the Solar Radiation Pressure torque is to adjust the relative position of the center of mass (c.m.) and the center of pressure (c.p.) of the solar sail. According to different generation principles of control torques,solar sail attitude control methods can be divided into two categories:those adjusting the center of mass,including gimbaled masses method25and sliding masses method26,27;those adjusting the center of pressure, including control vane method,28shifted or tilted wings method,17,29and controllable reflectivity method.30,31These methods involve mechanical movements, such as rotation or translation of the control mechanism. The IKAROS mission verified the effectiveness of attitude control by adjusting the reflectivity of the liquid crystal device,32but the areal density of liquid crystal device(about 200 g/m2) was much higher than the areal density of solar sail membrane (about 10 g/m2or less), and in order to effectively generate the control torque these devices were installed at the edge of the solar sail membrane. The mission was only a demonstration mission and still used gas jet thrusters as the main attitude control device.
For most attitude control methods, the mass of required control element increases sharply with the growth of solar sail area.The deformation of the sail membrane largely affects the attitude motion of a solar sail.33The magnitude of the torque generated by the deformation of the solar sail is proportional to the size of the solar sail, and can be theoretically used for attitude control of solar sails of various sizes. For example, a torque that can be used for attitude control is generated by adjusting the position of a wing tip along the boom in the method of billowed wings.34,35When the position of a wing tip changes, the shape of the wing is altered as well. The curvature in the wing will cause a change in the position of the center of pressure as well as the total solar radiation force vector acting on the wing, resulting in a torque. However, during the process of curling movement of the solar sail membrane,the actual deformation is very complicated, and deviates from simulation modeling based on many ideal hypotheses in the literature.Takao et al.proposed an attitude control method by a static waveform on the membranes.36,37The sail membrane is vibrated by mechanical actuators via tethers. When the frequency of the input vibration is synchronized with the spin frequency of the sail, the static waveform on the membranes can be created,and it changes the SRP force to produce the torque which can be applied for attitude control. Ceriotti et al. proposed a concept of Quasi-Rhombic Pyramid (QRP) solar sail for nanosatellites, providing a passive, self-stabilizing effect such that the apex of the pyramid will always point to the sun under SRP.38In addition, by varying the boom angles, it is possible to change the effective area-to-mass ratio of the spacecraft for attitude and orbit control.
From the perspective of technological development, the solar sail attitude control methods can be mainly divided into two categories: one is to combine the existing various attitude control methods in order to compensate for the disadvantages of each other. The other is to develop a new attitude control system by introducing cutting-edge results in other fields such as materials science, optics, and thermal science.
Researches about the vibration or deformation control of various structures such as cantilever beams are always of great importance in the field of materials science.39-43Shape memory alloys, piezoelectric ceramics and many other smart materials can be used for controlling the vibration or deformation.In recent years,due to the need of deploying large space structures and improving the ability of spacecraft to adapt to multiple missions,many researchers have conducted researches on deformation control of space structures.For example,the precise shape control of large space antennas with smart materials44,45; the shape control of a circular membrane space reflector by adjusting the surface reflectance across the membrane46,47; a new class of smart structures that is made of a number of cellular colonies, each consisting of a central pressure source surrounded by multiple cells48; an innovative self-deploying system for solar sail opening employing shape memory alloy elements49; the wrinkling growth and the deformed configuration control of the inflatable boom structure with a shape memory alloy wire actuator.50
Based on the concept of shape control, a solar sail attitude control method using the smart structures is proposed. The boom of the solar sail can deform by using smart materials such as piezoelectric ceramics actuators, and the deformation of the solar sail membrane due to boom deformation will produce a torque that is used for attitude control. The required voltage can be obtained by solar power generation from membrane solar cells without increasing additional battery. The weight of piezoelectric patch actuators is comparatively light and only distributed over the booms, so the additional mass and moment of inertia introduced by actuators are small.The magnitude of the control torque is proportional to the size of the solar sail. The method is applicable to the attitude control of various sizes of solar sails including large solar sails.The solar sail membrane and boom are connected by multiple points in this method,which are beneficial to weaken the influence of membrane vibration and flexibility during the deformation of the solar sail.
2. Model description
Several square solar sail architectures have been proposed.51In this paper, A square solar sail is assumed to have four booms that can deform independently. The solar sail membrane is connected to the booms through a multi-point connection method. When all booms are not deformed, the membrane is flat,the center of mass is designed to be at the geometric center of the sail,and the center of pressure coincides with the center of mass. As shown in Fig. 1, when the solar sail is not deformed, choosing the geometric center of the solar sail as the origin, the body-coordinate system O-xyz is established,boom OA is the positive y-axis (pitch axis), OD is the positive x-axis (yaw axis), the normal direction of the solar sail is the positive z-axis (spin axis). In this section, the expressions are described in the body-coordinate system unless otherwise stated. Lots of work about modeling beams with piezoelectric actuators” has been done and the exact solutions and analytical expressions of the bending problems has been obtained.52-55The purpose of this paper is to verify the concept of solar sail attitude control using shape variation of booms. In this paper, the deformation of the boom is based on the analytical expression in the literatures.55,56As shown in Fig. 1, taking boom OA as an example, its deformation has the following analytical expression in the body-coordinate system:
z=ayp(1)
where coefficient a and exponent p are both constants representing deformation.By changing the values of a and p,different deformation can be obtained.
It should be noted that deformation can make some sunlight blocked by a part of the solar sail (self-shadowing effect)or produce multiple reflection between solar sail membranes(multireflection effect). The two effects will cause thermal problems and uncertainties in SRP torque. For a solar sail with 30 m-long booms, assuming the coefficient a and the exponent p to be 0.0005 and 2, respectively, the selfshadowing effect appears when the angle between the sunlight and the solar sail plane is less than 0.03 radians. If the coefficient a is 0.001 and the exponent p is 2, the self-shadowing effect appears when the angle between the sunlight and the solar sail plane is less than 0.06 radians. This means that the self-shadowing does not happen in almost all of the halfplane range. Therefore, this paper limits the range of values of a and p to 0≤|a|≤0.001 and 1 <p ≤2, respectively. In the maximum deformation case, the length of the projection of the 30 m boom in the Y-axis is 29.982 m and its maximum curvature is only 0.002, the effect of deformation on the areal density of the membrane is ignored in this paper.
The Solar Radiation Pressure acceleration vector for the membrane asmay be written as57
where β is the lightness number, defined as the ratio of maximum SRP force to the solar gravity on the spacecraft, μsis the gravitational constant of the sun, r is the distance from the sail to the sun,n is the unit vector normal to the sail nominal plane, nsis the unit vector of the sunlight, {b1, b2, b3} are the sail force coefficients58,which depend on the optical properties of the sail film57, viz.
where ρsis the reflectivity coefficient, s is the fraction of specularly reflected photons, Bf(or Bb) is the front (or back) non-Lambertian coefficient, and εf(or εb) is the front (or back)emissivity of the sail surface.For a perfectly reflecting surface,ρs=s=1, which implies b1=b3=0, b2=1. But in fact,according to the Standard NASA Optical Coefficients updated in 201459, b1=0.0723, b2=0.8554, b3=-0.003. In particular, the presence of millimeter-scale wrinkles can reduce the specular reflection fraction from 0.94 to 0.8959,60. In this context, the sail force coefficients is b1=0.095, b2=0.8099,b3=0.015.
Wrinkles on the solar sail membrane are inevitable,and the boom deformation may lead to the formation of wrinkles.According to the above analysis, these factors will change the Solar Radiation Pressure acceleration vector.60,61However, considering that this change is small, in a preliminary mission phase, the solar sail membrane is assumed as a perfectly reflecting surface before and after deformation.
To prove that the structural deformation is negligible in our analysis, the response of the flexible sail with 30 m booms under SRP is simulated by ABAQUS.Suppose the SRP is vertically exerted on the sail surface, and the center of the sail is set to be fixed. The magnitude of the SRP is set to be 4.5×10-6Pa, which is the SRP strength at 1AU.
For comparison, we simulated the shape of the solar sail when it was undeformed and the shape of the solar sail when a boom is deformed (as shown in Fig. 1, the boom OA is deformed, a=0.001, p=2). Fig.2(a) shows that for the planar configuration sail, the maximum deviation of the membrane is 1.185 cm, and the overall deformation exhibits clear asymmetry. While Fig.2(b) shows that for the deformed configuration sail, the maximum deviation of the membrane is 7.535 cm, yet the deformation on the deformed side is significantly smaller than the planar side. Compared to the size of the solar sail, the deformation of the solar sail caused by non-rigidity is negligible,therefore,the effect of sail membrane vibration is not considered throughout this analysis. Before and after the deformation of the boom, the solar sail will be regarded as a rigid body and the sail membrane will be deformed along with the booms.
The membrane will slack if two adjacent booms deform at the same time.This paper does not consider these cases and the solar sail is always symmetrical about the x-z plane or the y-z plane. Except for the heliocentric gravitation and solar radiation force,other perturbation forces are neglected in this study.
2.1. Torque model
The solar sail membrane is composed of many rectangular elements as the HIJK in Fig.1(shaded part).These elements are parallel to the boom BD, and the projection in the plane yOz always coincides with the boom OA,regardless of whether the boom is deformed or not.When the boom OA has a deformation as in Eq.(1),the right half of the solar sail(the part ABD)will change into A’BD. The length of the boom OA remains unchanged. The coordinate of the point A’ is (0 yfzf)T. Obviously, zf=ayfp.
Since the element is a symmetrical parallelepiped about boom, the SRP force acting on the overall solar sail is a set of parallel force systems of equal magnitude, each of which can be described by a resultant force applied in the middle of the single element. Therefore, the SRP force applied on HIJK is equivalent to the resultant force at the point E.
The equation for calculating the torque produced by the element HIJK with respect to the solar sail center of mass is
where RGEis the position vector from the center of mass G to the point E,and FEis the resultant force acting on the element HIJK.
Define the coordinate of point E as(0,y,z)T,the coordinate of the centroid of the whole solar sail as (0, ycm, zcm)T, the coordinate of the centroid of the part A’BD as (0, y1, z1)T,the coordinate of the centroid of the part CBD as (0, y2,z2)T. Then, RGE, ycmand zcmcan be written as
where dmEis the mass of the element and m is the total mass of the right half of the solar sail. In particular,
where ρ is areal density of the membrane. Since the deformation of the solar sail is limited to a small range,the influence of the deformation on the surface density is ignored in this paper.L is the length of each boom, LEis the length from O to E along the boom and dL is the width of the element(the length of EF in Fig.1).Eq.(7)shows that LE,denoted as the function of the y coordinate of E. Next, use L(y) to represent LE.
In Eqs. (6) and (7), when a=0, the coordinate of the centroid of the undeformed BCD part can be calculated as Define the coordinate of the sunlight unit vector in the heliocentric ecliptic inertial reference frame as [Xs,Ys,Zs]T.The attitude orientation of the body-coordinate system with respect to the heliocentric ecliptic inertial reference frame can be described by the three Euler angles φ, θ, ψ. Three elementary rotations allow the two coordinate systems to overlap:the first rotation of the heliocentric ecliptic reference frame occurs around the x-axis at an angle φ,the second one around the new y-axis at an angle θ and the last one around the new zaxis at an angle ψ.The coordinate transformation matrix from the heliocentric ecliptic inertial reference frame to the bodycoordinate system is therefore
The torque generated by the deformed sail membrane A’BD can be calculated by integrating Eq. (16) on (0, yf).
It can be noted from Eq. (16) that the torque is related to the deformation coefficient a, the deformation exponent p,the attitude angles of the solar sail (φ, θ, ψ), the distance from the sail to the sun r, and the coordinate of the sunlight unit vector in the heliocentric ecliptic inertial reference frame[XsYsZs]T. The deformation coefficient a and the deformation exponent p are controllable variables, and the orientation of the solar sail body-coordinate system in the heliocentric ecliptic inertial reference frame is the control target.
The Force and torque generated by the deformation of the booms at different positions has a similar derivation process. For the sake of distinction, when the booms OA, OB, OC, OD deform, the corresponding deformation coefficients are denoted as a1, a2, a3, a4, whereas the deformation exponents are denoted as p1, p2, p3, p4. Corresponding to the deformation of the boom in each direction, the torque equations of the element are summarized as follows:
It can be seen from the above torque equations that when the booms OA and OC deform, only the torque around the x-axis can be generated, and when the booms OB and OD deform, only the torque around the y-axis can be generated.
When a3=0, the torque around the x-axis generated by the undeformed sail membrane BCD can be written as There are six combinations of deformations that can generate the torque around the y-axis or the x-axis, as shown in Table 1. When the boom deforms upward, Mx1 (or My4) is the torque generated when the boom OA (or the boom OD)is deformed; Mx2 (or My5) is the torque generated when the boom OC (or the boom OB) is deformed; Mx3 (or My6) is the torque generated when symmetrical booms are deformed.Mx4(or My1),Mx5(or My2)and Mx6(or My3)are the torques generated when the boom deforms downward.
2.2. Torque analysis
The time history of the attitude angles in the rendezvous mission with the Asteroid 2000 SG34462is employed to analyze the SRP torque. According to the position and velocity and the direction of the spin axis of the solar sail, the attitude angles φ and θ describing the body-coordinate system with respect to the inertial reference frame can be calculated. The SRP torque is related to the deformation coefficient a, the deformation exponent p, the attitude angles of the solar sail(φ, θ, ψ), and the coordinate of the sunlight unit vector in the heliocentric ecliptic inertial reference frame [XsYsZs]T.
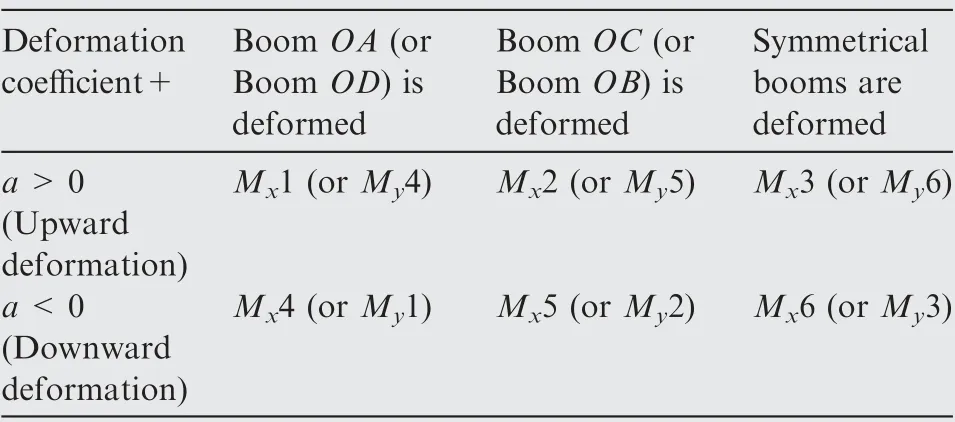
Table 1 Six combinations of deformations.
From Eq.(1),it can be seen that the coefficient a and exponent p are the control variables that characterize the degree of deformation. In order to study the effect of coefficient a and exponent p on torque, the attitude angles φ and θ, and the coordinate of the sunlight unit vector in the heliocentric ecliptic inertial reference frame [Xs,Ys,Zs]Tin Ref.62are used as relevant parameters as shown in Table 2.
Since the orbital driving force of the solar sail in the plane state has nothing to do with the spin angle ψ,the spin angle is not involved in the literature62, but it can be known from the torque equations that ψ will affect the torque of the solar sail in the deformed state.In Fig.3,the values of a and p are set to be |a|=0.001 and p=2.
It can be seen from Fig.3 that when the booms in the x-axis direction are deformed, the torque of the solar sail relative to the center of mass will change with the value of ψ. From the torque equation, this is because the value of ψ will affect the x-axis component of the sunlight vector in the body coordinate system nsx.At the same time,it can be seen that under the condition of any ψ value, the positive and negative torques can always be obtained through different combinations of deformation, indicating that the angle of the solar sail around the y-axis can be adjusted. When the booms are deformed in the y-axis direction, the torque Mxhas a similar changing law.
Fig. 4 shows the variation of the torque with the deformation coefficient a and the deformation exponent p.The value of ψ is set to be zero.It can be seen that the magnitude of the torque is proportional to the values of a and p. In the case of avoiding self-shadowing effect, the values of a and p are maximized in order to obtain the maximum torque. It should be noted that in order to avoid self-shadowing effect and multireflection effect,the values of a and p are limited to:0≤|a|≤0.001 and 1 <p ≤2,which means that adjusting the value of a alone can realize the continuous change of the solar sail from plane to deformation, while adjusting the value of p cannot achieve this goal. In the following research, the deformation exponent is set to be p=2.
Figs. 5 and 6 show the SRP torque that can be generated throughout the mission. In order to avoid self-shadowing effect,when the sunlight direction is close to the solar sail normal direction, the deformation coefficient a=0.8×10-3,while a=1×10-3in the remaining cases. When the boom deforms downward, a=0.8×10-3or a=-1×10-3.
Since the torque around z-axis is not generated,the value of ψ due to the coupling effect will be used as the reference variable. Without loss of generality, the initial value of ψ is set to be zero. Figs. 5 and 6 show that forward and reverse torques can be generated throughout the mission, thus enabling the adjustment of attitude angles φ and θ.
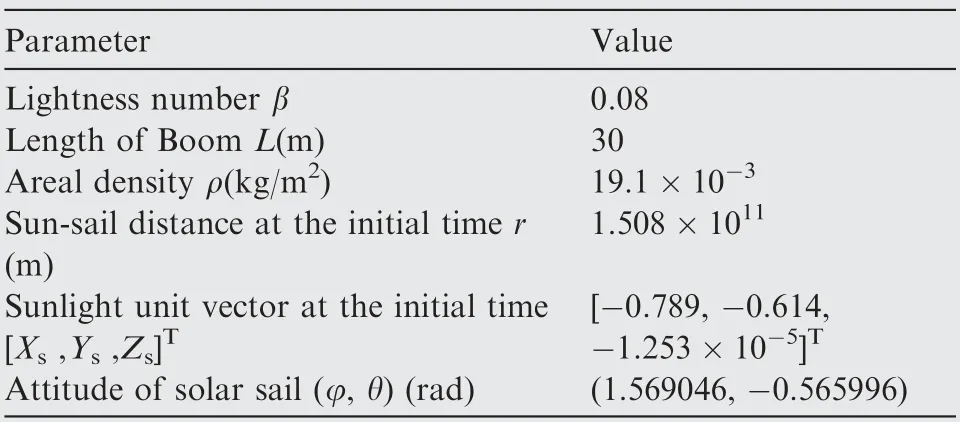
Table 2 The relevant parameters in torque analysis.
2.3. Attitude dynamics and kinematics
The deformation time of smart materials is usually very short.For example,the deformation time of piezoelectric ceramics is usually on the order of milliseconds. The deformation time of the boom is much shorter than the time of the attitude adjustment. Therefore, before and after the deformation of the boom, the solar sail will be regarded as a rigid body. In such a situation,the rigid body dynamics equation is still applicable.
The deformation will change the inertia matrix of the solar sail, but the variation of the inertia matrix is small due to the small variation.For example,when the length of the booms is L=30 m and the areal density is ρ=19.1×10-3kg/m2, the inertia matrix in different cases are shown in Table 3.
Therefore,for the sake of simplicity,the change of the inertia matrix is ignored in attitude dynamics.
The Euler angles and angular velocity can be used to describe the attitude kinematics and dynamics of the solar sail.Attitude dynamical equations can be derived from general rigid body dynamics.The attitude of the solar sail with respect to the heliocentric ecliptic inertial reference frame can be described by three Euler angles (φ, θ, ψ). The projection of the angular velocity vector of the solar sail in the bodycoordinate system is given as
The attitude dynamics can be obtained from the angular momentum theorem of a rigid body, that is
where Mz=0.
Because Mxand Myis related to the distance from the sail to the sun r and the coordinate of the sunlight unit vector in the heliocentric ecliptic inertial reference frame [Xs,Ys, Zs]T, the changes of r and [XsYsZs]Tdue to the effect of the orbit motion are considered during the attitude adjustment.
2.4. Attitude maneuver
The SRP vector direction of the solar sail coincides with n due to the assumption of ideal solar sail. If the direction of the n can be controlled, the trajectory of the solar sail can be controlled as well.
As shown in Fig. 7, let the spin axis (z-axis in the bodycoordinate system) unit vector of the solar sail be defined as nz.The components of nzin the heliocentric ecliptic inertial reference frame O-XYZ is
where c′123which is transposed with respect to c123,is the coordinate transformation matrix from the heliocentric ecliptic inertial reference frame to the body-coordinate system.
It can be noted from Eq.(24)that the direction of nzin the heliocentric ecliptic inertial reference frame can be controlled by adjusting φ and θ.Therefore, although the attitude control method discussed in this paper cannot generate a torque around the z-axis, it can still achieve the adjustment of the SRP vector.

Table 3 Inertia matrix in different cases.
3. Numerical examples
The attitude control and orbit control of solar sails are strongly coupled. That is to say, the attitude change of the solar sail will affect the orbital driving force of the solar sail,and the change of the orbit position of the solar sail will affect the magnitude of the attitude control torque. In the preliminary design of the solar sail mission, the attitude angle is usually taken as the control variable of the SRP, and assumed to be changed instantaneously and continuously. By designing the attitude angles of the solar sail,specific mission objectives,such as time-optimal orbital transfer, can be achieved. However, in the actual flight of solar sails, the attitude adjustment usually needs to be conducted periodically. Therefore, the effect of the orbital motion on the attitude control torque must be considered in the attitude adjustment. In this section, the effectiveness of the proposed attitude control method will be demonstrated.
3.1. Examples of attitude adjustment
In this case,the effect of the proposed method in a single attitude adjustment process is evaluated. The attitude profiles obtained in the literature62for a solar-sail orbital transfer mission is considered. In the literature, a solar sail with the lightness number β=0.08 is used to realize the rendezvous mission from the earth to the Astroid 2000 SG344. According to the optimized results in the literature, the departure time of thesolar sail is MJD 59721.2196 and the initial attitude angles are φ=1.569046 rad, θ=-0.565996 rad. Assuming that the attitude angles can be changed instantaneously and continuously, the solar sail will rendezvous with the Astroid 2000 SG344 after 360.368 days. Without loss of generality, in the actual flight process, it is assumed that the attitude angles of the solar sail are adjusted once a day, with the initial value being the current attitude angles and the target value being the attitude angles one day later. The attitude control method proposed in this paper is adopted to test the one single segment attitude adjustment.According to the different process of attitude adjustment,two schemes are used to realize the one single attitude maneuver: The Rest-to-rest Attitude Angle Adjustment and the Attitude Angles Change with Approximately Constant Angular Velocity. Simulation parameters are shown in Table 4.

Table 4 Simulation parameters of single attitude adjustment.
For an ideal plane solar sail, the SRP force is independent of the spin angle ψ,therefore,the change of ψ is not considered in literature.62For the solar sail in deformed state, the magnitude of the control torque will be affected by the spin angle ψ,so the change of ψ due to coupling effect needs to be considered in this paper. Since the torque around z-axis cannot be generated by the above-mentioned attitude control method,the value of ψ is not controlled. Without loss of generality,assuming ψ=0 at the initial time.
(1) The rest-to-rest attitude angle adjustment scheme
In this scheme,both the initial angular velocity and the target angular velocity are set to be zero.The attitude change process of the solar sail is shown in Fig. 8.
Fig.8 shows that the attitude adjustment time is about 350 seconds, which is much shorter than the planned time (one day), indicating that the expected attitude adjustment goal can be achieved using the above-mentioned attitude control method. Although the torque around z-axis is not generated during the deformation of the boom, the solar sail slightly rotates around z-axis due to the coupling effect.
(2)The attitude angles change with approximately constant angular velocity
The scheme that the Attitude Angles Change with Approximately Constant Angular Velocity also can be considered.When the solar sail is not deformed,Mx,Myand Mzare zero.For the square solar sail, Ixand Iyare generally the same.According to Eq. (23), the angular acceleration of the square solar sail in the undeformed stage is approximately zero. That is to say, the angular velocities ωxand ωyarrive the target value through the solar sail deformation. And then the solar sail will be flat, and transfer to the attitude with a constant angular velocity until the next stage of adjustment. Because the deformation time of solar sail is very short relative to the time span of each attitude adjustment stage, the deformation time of solar sail is ignored when calculating the target value of angular velocity. Assuming the initial angular velocities are [ωxωyωz]T=[0 0 0]Trad/s. According to Eqs. (20) and(23), the target angular velocity is calculated as [ωxωy]T=[1.239×10-101.557×10-7]Trad/s. The attitude change process of the solar sail in this stage is shown in Fig. 9.
As seen from Fig. 9, the time of the boom deformation is very short, and the attitudes change little during this time.Therefore, although the simplified method adopted in the scheme makes the adjusted attitude angles deviate from the target values, the differences are very small.
Compared with the Rest-to-rest Attitude Angle Adjustment Scheme, this scheme has lower attitude adjustment accuracy,but greatly reduces the number of time variables,which is conducive to improving the efficiency of solving nonlinear programming problems.
3.2. Example of orbit-attitude coupled control
As mentioned at the beginning of this section,the attitude and orbit control of the solar sail are coupled. In this case, the influence of the attitude control on orbit will be studied.Referring to the example used in 3.1 section, the attitude angles scheme with continuous change in Ref.62is discretized according to a fixed attitude adjustment period (once a day).In each period, the Rest-to-rest Attitude Angle Adjustment Scheme is adopted to achieve the attitude maneuver, so as to realize multiple adjustments from the current attitude to the target attitude. According to the adjustment of attitude in each period and combining with orbit dynamics, the differences between ideal orbit(attitude angles are assumed to be changed instantaneously and continuously)and actual control orbit are compared.
In Fig.10,the black line represents a series of instantaneous attitude adjustments required to achieve the optimized trajectory in the Ref.62The red line represents the actual attitude adjustment by the method proposed in this paper. It can be seen that the change of the attitude angles of the actual attitude adjustment is basically the same with the ideal reference attitude angles. At the same time, it should be noted that the change of ψ due to coupling effect is very small.
In Fig. 11, the black line represents the trajectory of the solar sail obtained by optimization calculation in the literature.62The red line represents the actual trajectory considering the orbit-attitude coupling effect. It can be seen that the trajectories are basically the same. The final error of the position is about 50000 km.
4. Conclusions
The research shows that the attitude adjustment of the solar sail around the pitch and yaw axes can be effectively achieved by the deformation of the solar sail booms.The proposed solar sail attitude control method has many advantages such as simple structure, small introduced disturbance, low additional load, and unrestricted application by the size of the solar sail.Therefore,this method has potential applications in the field of solar sail attitude control.However,spin angle cannot be controlled without a torque generated around the spin axis, thus affecting both the magnitude of the control torque and the time required by attitude adjustment.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
This study was supported by the National Natural Science Foundation of China (Nos. 11772167, 11822205).
 CHINESE JOURNAL OF AERONAUTICS2022年10期
CHINESE JOURNAL OF AERONAUTICS2022年10期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Full mode flight dynamics modelling and control of stopped-rotor UAV
- Effect of baffle injectors on the first-order tangential acoustic mode in a cylindrical combustor
- Experimental study of hysteresis and catastrophe in a cavity-based scramjet combustor
- Flow control of double bypass variable cycle engine in modal transition
- Effects of chemical energy accommodation on nonequilibrium flow and heat transfer to a catalytic wall
- A reduced order model for coupled mode cascade flutter analysis
