Fault diagnosis of bearings based on deep separable convolutional neural network and spatial dropout
Jiqing ZHANG, Xingwei KONG,b,c,*, Xueyi LI, Zhiyong HU,b,c,Liu CHENG, Mingzhu YU
a School of Mechanical Engineering and Automation, Northeastern University, Shenyang 110819, China
b Key Laboratory of Vibration and Control of Aero-Propulsion System, Ministry of Education, Northeastern University,Shenyang 110819, China
c Liaoning Province Key Laboratory of Multidisciplinary Design Optimization of Complex Equipment, Northeastern University, Shenyang 110819, China
d Angang Steel Company Limited, Anshan 114021, China
KEYWORDS Batch normalization;Convolutional neural network;Fault diagnosis;Similarity pruning;Spatial dropout
Abstract Bearing pitting,one of the common faults in mechanical systems,is a research hotspot in both academia and industry.Traditional fault diagnosis methods for bearings are based on manual experience with low diagnostic efficiency. This study proposes a novel bearing fault diagnosis method based on deep separable convolution and spatial dropout regularization. Deep separable convolution extracts features from the raw bearing vibration signals, during which a 3 × 1 convolutional kernel with a one-step size selects effective features by adjusting its weights. The similarity pruning process of the channel convolution and point convolution can reduce the number of parameters and calculation quantities by evaluating the size of the weights and removing the feature maps of smaller weights.The spatial dropout regularization method focuses on bearing signal fault features,improving the independence between the bearing signal features and enhancing the robustness of the model.A batch normalization algorithm is added to the convolutional layer for gradient explosion control and network stability improvement.To validate the effectiveness of the proposed method, we collect raw vibration signals from bearings in eight different health states. The experimental results show that the proposed method can effectively distinguish different pitting faults in the bearings with a better accuracy than that of other typical deep learning methods.
1. Introduction
Bearings are widely used in transmission mechanisms, actuators, and other mechanical equipment, playing a vital role in aerospace,transportation,industrial manufacturing,and other fields.1Therefore, condition monitoring and timely health management of bearings are critical in reducing maintenance costs and improving operational safety.2However, development in current machinery and the growing tendency of equipment toward intelligence, efficiency, and precision impose significant challenges for traditional methods in accurate machinery diagnosis under complex coupled conditions.3With the deepening of the research on fault diagnosis technology of bearings and other rotating machinery,a variety of fault diagnosis methods have emerged, such as noise analysis method,4acoustic emission analysis method,5,6oil analysis method,7fuzzy diagnosis analysis method,8and vibration analysis method.9,10Literature review shows that vibration analysis can accurately determine the type and location of the fault and is therefore widely used in practical engineering applications. The diagnosis technology for bearings and other rotating machinery based on vibration signal analysis usually involves three steps: the acquisition of vibration signals, the extraction of fault feature information, and fault type identification.11Among these steps, the acquisition of vibration signals is the basis of fault diagnosis. The accurate and effective extraction of fault feature information from vibration signals plays a decisive role in obtaining correct diagnosis results.According to different analysis domains, the diagnosis techniques based on vibration analysis mainly involve timedomain analysis, frequency-domain analysis, and time-frequency analysis.12The time-frequency analysis technology can judge the running state of bearings and other rotating machinery according to the dimensionless indexes such as the mean value, variance, maximum value, minimum value margin,and peak value. The time-domain synchronous average,13adaptive noise elimination,14autocorrelation analysis,15and other methods are also included. The time-frequency analysis technology is more effective in early fault detection, while less effective for compound fault of bearings and other rotating machinery. Compared with the time-domain analysis technology, frequency-domain analysis is more intuitive in reflecting fault signal feature changes, and is therefore widely used.Frequency-domain analysis obtains various frequency information in the signal through Fourier Transform. Currently,commonly used frequency-domain analysis techniques include power spectrum,16cepstrum,17and demodulation spectrum.18The frequency-domain analysis method is effective for stationary signals instead of non-stationary and nonlinear signals.Processing non-stationary and nonlinear signals requires combination of time-frequency techniques,such as empirical mode decomposition,19,20variational mode decomposition,21,22wavelet analysis,23,24nonlinear mode decomposition,25and local mean value decomposition.26,27
Many scholars have attempted to use time-frequency analysis techniques to extract the feature information contained in fault signals. Liu et al.28combined the short-time Fourier Transform with the sparse autoencoder to analyze and diagnose the fault acoustic signals of rolling bearings. Lopeze-Ramirez et al.29used the short-time Fourier Transform to analyze the fault signals of induction motor bearings and effectively judged them by identifying different spectral components.Chen et al.30proposed a line Frequency Modulation(FM)Wigner-Weil distribution based on the Wigner-Weil distribution, combining polynomial and spline functions to extract the instantaneous frequency components of the signal.Chen et al.31analyzed the internal production process of wavelet transform and performed fault analysis on non-smooth signals of rotating machinery. While these methods are useful in fault diagnosis for rotating machinery, problems still remain.The first problem is that these methods require manual feature extraction and a priori knowledge of signal processing techniques. Another problem is that these features are extracted based on specific diagnostic conditions and may not apply to other conditions.
Rapid development in increasingly efficient chips enables wide application of deep learning and artificial intelligence to fault diagnosis.Most current fault diagnosis approaches focus on methods that use pre-extracted features as input to a neural network. Yuan and Tian32used a GRU neural network for sequential data diagnosis in dynamic processes. Chen and Zhao33used wavelet transform to extract features of signals on different channels as input to a neural network for bearing fault classification. Huang34extracted the main fault information components using singular value decomposition and empirical mode decomposition. They extracted the fault feature parameters from the selected eigenmode function components as the input to the neural network for bearing fault diagnosis.Zhang et al.35extracted the bearing vibration signal features with an autoregressive model and implemented fault identification by optimizing artificial neural networks. Wang et al.36directly used the Hilbert envelope spectrum of the sampled bearing signal as the feature vector.They later used a deep belief network to classify the feature vector to complete the bearing fault diagnosis. Khajavi and Keshtan37used the discrete wavelet transform for signal pre-processing, classifying the bearing faults through a neural network using the normalized discrete wavelet coefficients of the input. Yu et al.38employed the bidirectional long short term memory network to diagnose early faults in gears. The above methods are constrained by the need to preprocess features, ignoring the powerful nonlinear fitting capability of neural networks that can inherently extract features and perform classification. This research uses deep separable convolutional neural networks,batch normalization, and spatial dropout regularization to improve the performance of deep models.
We first establish a deeply separable convolutional neural network to reduce parameters and computation quantity,adopting the layer-by-layer convolution and the point-bypoint convolution. A spatial dropout layer is then built to diversify its learning features and prevent overfitting. Finally,a batch normalization layer is constructed to standardize the specified corresponding feature axis. The input values of each layer are normalized in a normal distribution with a mean value of 0 and a variance of 1.Experimental results show that this method is more effective than the single deep model and other deep learning methods. It has the following significant advantages in bearing fault diagnosis:
(1) Compared with the traditional one-dimensional convolutional neural network, this method can reduce the model parameters by about 60% while maintaining good diagnostic performance.
(2) The raw vibration signals are trained directly without time-frequency conversion,reducing the repetitive manual workload.
(3) It can solve the problem of update coordination between networks, accelerate training and convergence speed,and effectively prevent overfitting.
(4) It uses a 3 × 1 small-scale convolutional kernel with a one-step size, automatically adjusting the weights and selecting effective features during training.
The rest of this article is organized as follows. Section 2 describes the approach proposed in this study, introducing the deep separable convolution,batch normalization,and spatial dropout regularization, and emphasizing the difference between traditional convolution and deep separable convolution. In Section 3, the effectiveness of the proposed method is validated by an experiment, and the experimental results are analyzed.Section 4 presents the results and discussion.Section 5 presents the conclusions.
2. Methodology
the rolling bearings,passed through the separable convolution layers, batch normalization layers, spatial dropout layers, and pooling layers, and then input to the fully connected layer through global maximum pooling.
The softmax classifier is used to diagnose the healthy states of bearings. A 3 × 1 convolutional kernel with a one-step size is chosen to automatically adjust the weights and select effective features in the stacked one-dimensional separable convolutional layers. The deep separable convolution includes two pruning processes: layer-by-layer convolution and point-bypoint convolution. In the layer-by-layer convolution process,the similarity of the filters is measured by the K-L scatter,and similar filters are cropped out to reduce redundancy. In the point-by-point convolution process, the importance of the input feature map in the linear combination is assessed by the weights. The small weight and its associated feature channels are clipped out. The number of tracking network parameters is thus reduced by the above two convolution processes. In addition to achieving downsampling, we apply the spatial dropout strategy to the convolutional layer, focusing on the bearing fault signal features. The spatial loss helps to improve the independence between the features and reduce the risk of network overfitting, enhancing the robustness of the whole model. Moreover, a batch normalization algorithm is added to the convolutional layer to solve the update coordination problem among multi-layer networks to ensure the consistency of data distribution.
2.1. Deep separable convolution
Deep separable convolution consists of layer-by-layer convolution and point-by-point convolution to reduce computation and the number of parameters. W and H are channel length and width, respectively; S is the channel number;W × H × S is the input shape. Suppose that convolution2D has K 3 × 3 convolution; the stride is set to one; then the calculation quantity of convolution2D is W×H×S×K×3×3.∑is the summation symbol of the output feature map.b is the bias constant.The separable convolution2D is divided into C groups,get K convolution features by the number of channels.Then we carry on the N 1×1 convolution and obtain N pointby-point convolution feature maps.Fig.2 presents the process of the deep separable convolution,and Fig.3 presents the traditional convolution process.
where KLis the layer-by-layer convolution kernel, and NPthe point-by-point convolution kernel.
Assume that the size of the input feature graph is H × W,the number of the channels is S,the convolution kernel size is Df× Df, and the number of convolution kernel is K; then the quantities of traditional convolution and deep separable convolution are.
It can be seen that the computation reduction of the deep separable convolution is related to the output channel K and the size of convolution kernel Df× Df. In practice, a 3 × 3 sized convolution kernel is generally used for deep separable convolution. If the output channel is 64, then the calculation amount for deep separable convolution by Eq.(5) is only 0.126 times that of the traditional convolution parameter calculation.
2.1.1. Layer-by-layer convolution and similarity pruning
In layer-by-layer convolution,the decreased number of output channel feature graphs K leads to parameter calculation reduction.The input channel feature graphs M is convolved with filter K, also called deep convolution. In this process,convolution computation only occurs in the internal of each channel; information between channels is not fused, and spatial features are mainly extracted.
During layer-by-layer convolution, similar filters can complement each other.After one of them is removed,the remaining similar filters can still ensure their network accuracy in the
process of retraining, thus reducing the complexity of the network. We use the KL divergence method to measure the similarity of the filters.39The asymmetry of KL divergence between the two filters is used to ensure the distance assessment of the similarity of the two filters.The calculation process is.
where P is the original probability distribution, Q denotes the approximate probability distribution, P||Q represents the information loss generated when the approximate probability distribution Q is used to fit the original probability distribution P,p(xi)and q(xi)represent the weight ratios at the corresponding positions of the filter, respectively.
The filter with a high entropy value is retained when we delete similar filters. A similar filter is evaluated by crossentropy, and the filter with low cross-entropy is deleted to ensure the richness of the reserved filter. The comentropy is defined as.
where p(xi)is the probability of event X=xi,and lg(p(xi))the information of event X = xi. X is a discrete random variable whose values are set to X = x0, x1, ..., xn.
The similarity pruning of the feature map algorithm in layer-by-layer convolution is conducted as follows.
Input: The filters in layer-by-layer convolution and the pruning hyperparameters.
Output: The removed filters.
Step 1. Normalize filters of the current layer.
Step 2.Calculate the KL scatter between the two filters and sort the filters from the smallest to the largest by distance.
Step 3. Take the prune hyperparameters as a threshold value and similar filters as the ones to be pruned.
Step 4. Calculate the cross-entropy of the filters to be pruned and remove the filters with small cross-entropy.
2.1.2. Point-by-point convolution and weight pruning
In point-by-point convolution,feature graphs K and 1×1×N filters are convolved layer-by-layer output. Since there are N 1 × 1 × N convolution kernels in the point-by-point convolution, N channel feature graphs are finally output. In this process, the feature fusion of the input feature map at the channel level is realized through point-by-point convolution,also known as point-wise convolution.
In the deep separable convolution, computation mainly concentrates on the point-by-point convolution; therefore,deleting the feature graph with a small weight value to reduce calculation and the corresponding parameters is considered.
where K1,K2,...,Knrepresent 1×1×N filters,and F1,F2,...,Fkthe feature graphs of input K.
The output of point-by-point convolution can be regarded as a multinomial linear combination of the input feature graphs. Therefore, if the weight value in a certain channel in the convolution is minimal, deleting the unimportant feature graph and its weight can be considered. The pruning process is shown in Fig. 4.
In layer-by-layer convolution, similar filters complement each other. Once one of the filters is removed, the remaining filters can supplement each other during the retraining process to maintain network accuracy. Before the model training, the weights are initialized randomly, and then the forward propagation, loss calculation, and back propagation are conducted.The weights are updated by the random gradient descent method until the loss function converges to the minimum.
2.2. Batch normalization
Batch normalization is a layer used after a convolutional layer or a dense connection layer to standardize the input data by receiving a bias parameter specifying the corresponding feature axis. Batch normalization could be adaptive to parameter initialization. The transforming method at each level makes the mean to be 0,the variance of 1 normal distribution.Moreover,falls in each layer activation function area are more sensitive,solve the problem of the update coordination and the data distribution between the network layers. Therefore, the primary functions of batch normalization accelerate network training and convergence, control gradient explosion, prevent overfitting, and improve network stability. The batch normalization algorithm is divided into the following four steps.
Step 1. Calculate the mean value of each training batch.
Step 2. Calculate the variance of each training batch.
Step 3. Normalize the training data of the batch with the obtained mean value and variance, and obtain the 0-1 distribution.
Step 4.Conduct scale transformation and migration for the normalized training.
Specific algorithms of batch normalization are as follows:
where ε is a tiny positive number used to avoid a divisor turning 0, γ is the scale factor, and β the translation factor.
Fig.5 displays the convolutional neural network after batch normalization. The batch normalization is added after each hidden layer before transforming the nonlinear function and after obtaining the x activation value.
The model metrics on the training set has a significant decreasing trend with batch normalization, and the Root Mean Square (RMS) error tends to be constant with the increase of the training period.39Conversely,there is no significant decrease in the model RMS error without batch normalization, and exists no convergence trend or fitting trend of the model. In the testing set, the RMS error of the model with batch normalization tends to decrease significantly as the training period increases,indicating that the predictive performance and the generalization ability of the network gradually increases. On the contrary, the RMS error of the model without batch normalization did not show a decreasing trend on the testing set, and the model performance did not improve with the increase of training cycles. Thus, the model did not have substantial prediction performance.
2.3. Spatial dropout algorithm
The spatial dropout strategy is an improvement in the dropout strategy. Traditional dropout randomly sets some elements to zero, which means that the neural network may set the other part of the elements to zero in the next training.Usually,adjacent elements are strongly correlated, and randomly setting some elements to zero will reduce the learning ability of the network. The spatial dropout randomly sets all elements of a specific dimension to zero, which helps to retain relevance between the features and enhances robustness of the model.Fig. 6 presents the principle diagrams of dropout and spatial dropout.
Fig. 7 shows the one-dimensional convolution layer using the dropout strategy and the spatial dropout strategy process.The top of the first and second lines represent the convolution kernels of pixel features 1 and 2. The bottom layer before the third line represents the output,and the gray square in the figure stands for the discarded element. In backpropagation, the transformation of convolution kernel W2is conducted according to the features F2, and e is the error function.
Fig. 7(a) shows the use of the conventional dropout algorithm, where f1bis the discarded neuron and f1ais the undiscarded neuron. Since F2and F1are the outputs of a convolutional layer, f1aand f1bhave a strong correlation: f1a≈f1b,or de/df1a≈de/df1b.In Fig.7(a),although the contribution gradient of f1bis 0, there is a strong correlation between f1band f1a, and the learning efficiency is not improved.
Fig. 7(b) represents the spatial dropout algorithm. In this method, for a convolution feature tensor with a size of n-× length × width (where n is the number of features), only perform the dropout method for n times as if a certain channel was randomly discarded. After the spatial dropout, the adjacent feature s is either 0 or activated.
Experiments show that the improved method is more effective in spatial dropout training.40
3. Fault simulation experiment on rolling bearing
To validate the effectiveness of the proposed method, we design an experiment at the constant speed of 1800 r/min.The raw vibration signals of the bearing are obtained by an acceleration sensor of type PCB 352C65, with sensitivity of 103.0 mV/g, output bias of 10.9 VDC, transverse sensitivity of 0.8%,resonant frequency of 58.3 kHz,and a discharge time constant of 1.6 s.
Then we separate and convolve the raw vibration signals to classify the faults of the normal bearing,the outer ring,and the inner ring of the bearing. The sampling frequency is set to 19.2 kHz, and the sampling time for each state 110 s. The acceleration sensor is mounted on the housing of the bearing seat. The testbed is shown in Fig. 8.
The test device consists of a motor frequency conversion controller, a motor, a coupling, a bearing seat, a rotor, and other parts. Eight health conditions of bearings are designed in this experiment, including 1 normal condition, 3 inner ring faults, and 4 outer ring faults. N205EM and NU205EM are used to simulate the faults of outer rings and inner rings,respectively.Fig.9 shows the health conditions of eight groups of different bearings. The main parameters of the cylindrical roller bearings are shown in Table 1.
The raw vibration signals of the bearings are displayed in Fig. 10. The contact of defects on the inner and outer ring raceways will cause shock effect, when the frequency amplitude will increase abruptly. The frequency will be relatively smooth when no defective contact exists,leading to the similarity of the time domain signals.
As shown in Fig.10,condition(1),(3),and(6)have distinct peaks, different from the other five signals. The fault impact point can be seen in conditions (6) and (8), while conditions(7) and (8) have both similarities and differences. It is almost impossible to distinguish the fault from the bearing vibration signals by naked eyes. Therefore, we build a convolutional neural network model to recognize these similar time-domain signals to achieve a better classification of faulty bearings.
The data are checked for outliers before input into the machine learning model, and if data cleansing is required,the outliers should be removed in advance. Fig. 11 is the histogram of the sample numbers of four different bearing health states.The normal condition,one type of inner ring faults,and two types of outer ring faults are randomly selected from the eight bearing health states. 2500 points were selected from the normal condition and inner ring faults respectively, and 4000 points and 3500 points were selected from the two types of outer ring faults respectively, are used to draw the histogram,which shows that the health states of the four bearings are normally distributed. These raw data are then used for bearing fault detection.
The training set, validation set, and test set are not duplicated. The sample numbers of the three sets are 20,008,2,496, and 2,496, respectively. The numbers of channels in the deep separable convolutional network are 32, 64, 64, and 64. The activation function is the Rectified Linear Unit. The data are processed by Python on Intel i7-10700 CPU and NVIDIA GeForce GPU.Table 2 shows the details of the proposed method,including the output shape and number of parameters of each layer.
4. Results and discussion
In deep learning, the loss function is the key to learning process configuration, and the model needs to minimize its loss value during training. The loss function can also evaluate the achievement effectiveness of current tasks, guiding the model learning.The model parameters are modified by backpropagation according to the loss function.
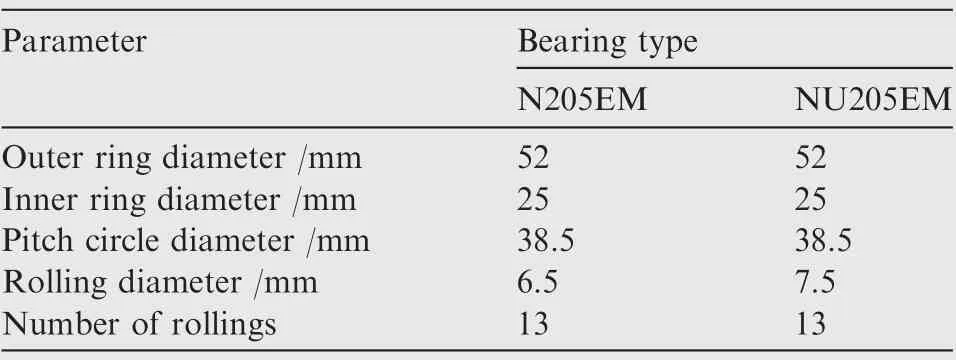
Table 1 Main parameters of cylindrical roller bearings.
The softmax loss function is a classifier. The softmax uses the logic function and normalized exponential function to provide the posterior probability of the classification label, which is mapped to the [0, 1] interval. At the last output node, the node with the maximum probability is selected as the prediction target of a bearing health state. For fault diagnosis problems,the probability values indicate the probability of bearing health status belonging to a certain category.
The softmax classifier is adopted in this study, and the calculation formula is.
where yiis the output of the jthneuron in the output layer, m the number of classes of the bearing failure,and p(yi)the probability output of the neuron after softmax.
In this study, eight bearing fault vibration signals are consistently acquired at 1800 r/min. We divide the acquired data set into the training set, testing set, and validation set according to the ratio of 8:1:1.Fig.12 shows the relative accuracy of the convolutional neural network model on the training and validation sets for epochs from 0 to 450. When the epoch is 60,the accuracy of the training and the validation sets is about 90%,signifying the beginning of rapid convergence of the neural network model. When the epoch is larger than 240, the accuracy difference between the training and the validation sets is small, proving the non-existence of overfitting in the proposed convolutional neural network model. Finally, when the epoch is 450, the accuracy of the training and the validation sets reaches about 98%, showing a good classification of the proposed bearing fault diagnosis model.
A confusion matrix is used to summarize the results of a classifier. The eight-component classification in this study is an 8 × 8 table, with each row indicating the number of actual samples in that class, and each column the number of samples predicted to be in that class. After generation of the classification results, matplotlib can be used to visualize the confusion matrix.
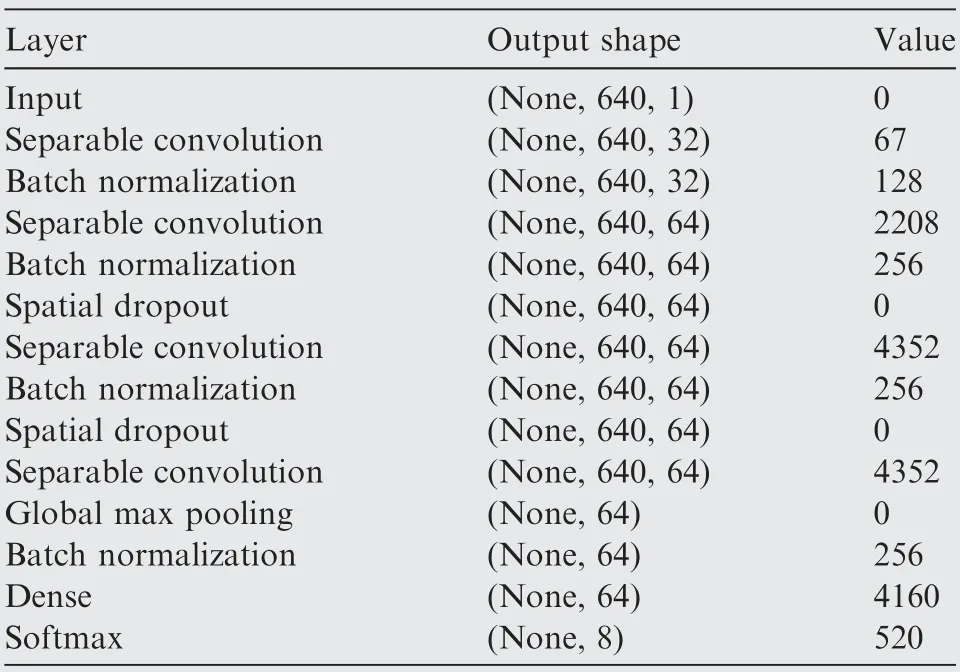
Table 2 Network details and main parameters.
Fig. 13 presents the confusion matrices of the training set,validation set, and testing set. The results show a good effect of the method on the raw vibration signal of the bearing under mixed conditions. There are 2501 samples in the training set,with a classification accuracy of 97.87%. Except for condition(4),the accuracy of the other conditions is above 95%,among which the accuracy of conditions(6)and(7)is 100%.The validation set has 312 samples with a classification accuracy of 97.38%. Except for conditions 3 whose accuracy is below 90%, the accuracy of all the other conditions is above 95%,with that of conditions (6), (7), and (8) being 100%. The testing set has 312 samples, and the classification accuracy is 97.75%. Except for condition (3) whose accuracy is 88.5%,the accuracy of the other conditions is higher than 95%,among which the accuracy of conditions (2), (6), (7), and (8)is 100%.
To verify the effectiveness of the proposed method in vibration signal feature extraction, t-SNE visual samples are processed. t-SNE is an embedding model for mapping data in high-dimensional space to low-dimensional space and retaining the local characteristics of the data set. It transforms the similarity between data points into conditional probabilities.The Gaussian joint distribution expresses the similarity of data points in the original space, and the t-distribution represents that in the embedding space.
Fig. 14 shows the 3D results of t-SNE visualization, and it incicates that the series features of the eight kinds of bearing conditions are accurately clustered. The three-dimensional images show apparent clustering of the cascade features obtained by the method, indicating the effectiveness of the method in feature extraction from vibration signals.
Compared with the traditional one-dimensional convolutional neural network, the deep separable convolution based on spatial dropout proposed in this study can reduce the network parameters by about 60% with good diagnostic performance. As shown in Table 3, the testing set accuracy of this method reaches 97.75%, which is as good as the traditional convolutional neural network. The proposed model is also superior to those using Dropout or spatial Dropout based on traditional convolutional neural networks only. In terms of the testing accuracy alone, this method is about three to four percentage points higher than those using only traditional convolution or dilated convolution, indirectly validating the accuracy of the proposed method for multi-classification.
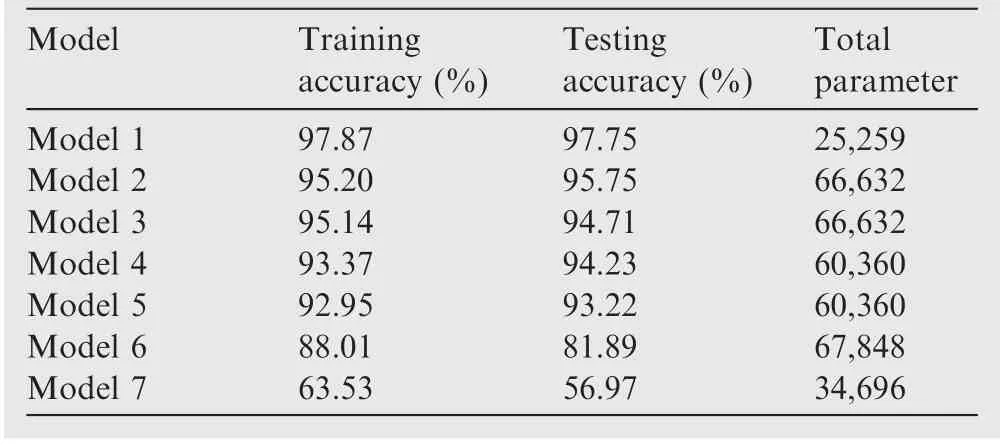
Table 3 Comparison between proposed method and other typical diagnostic methods
Table 3 shows the comparison between the proposed method(Model 1)and other typical diagnostic methods.Models 2-7 are the traditional convolutional neural network and spatial Dropout, the traditional convolutional neural network and Dropout, the traditional convolutional neural network,the dilated convolutional neural network, the method using a Gated Recurrent Unit neural network for sequential data diagnosis in dynamic processes,33and the bearing fault diagnosis method using a bidirectional long and short time memory network,41respectively.
According to Table 3,Model 1 obtains the highest accuracy of 97.75%on the test set.Compared to the training parameters of Models 2-5,those of Model 1 are reduced by 60%,allowing significant savings in training time and computational resources. Model 7 has a lower accuracy on both the training and test sets, apparently requiring improvement. In summary,the proposed method can accurately diagnose bearing faults,and provide better diagnostic accuracy with fewer model parameters than other models.
5. Conclusions
This study proposes a new fault diagnosis method for bearings,which can directly learn the raw vibration data to realize fault diagnosis. The experimental results show that this method effectively learns the features with an excellent diagnostic effect on the bearing faults. Compared with the traditional artificial feature extraction method, it significantly reduces dependence on manual labor. In addition, the accuracy of this method is higher than 97% with only half the network parameters of the traditional convolutional neural network. Our future research work will focus on the downsampling and selection of valuable features using small-scale convolutional kernels.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work is supported in part by the National Key Research and Development Program of China (No. 2019YFB1704500),the State Ministry of Science and Technology Innovation Fund of China (No. 2018IM030200), the National Natural Foundation of China(No.U1708255),and the China Scholarship Council(No.201906080059).The authors are grateful for Dr. Hui MA who provided the experimental equipment.
 CHINESE JOURNAL OF AERONAUTICS2022年10期
CHINESE JOURNAL OF AERONAUTICS2022年10期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Full mode flight dynamics modelling and control of stopped-rotor UAV
- Effect of baffle injectors on the first-order tangential acoustic mode in a cylindrical combustor
- Experimental study of hysteresis and catastrophe in a cavity-based scramjet combustor
- Flow control of double bypass variable cycle engine in modal transition
- Effects of chemical energy accommodation on nonequilibrium flow and heat transfer to a catalytic wall
- A reduced order model for coupled mode cascade flutter analysis
