Analytical solutions for Earth discontinuous coverage of satellite constellation with repeating ground tracks

Xiangyue HE, Haiyang LI,*

a College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China

b Hunan Key Laboratory of Intelligent Planning and Simulation for Aerospace Missions, Changsha 410073, China

KEYWORDS Analytical model;Coverage region;Earth discontinuous coverage;Repeating ground track;Satellite constellation;Two-dimension map of visibility properties

Abstract This paper presents an analytical model for calculating the Earth discontinuous coverage of satellite constellation with repeating ground tracks by integrating and extending the application of coverage region and route theory. Specifically, the visibility condition for a ground point is represented as a coverage region in the two-dimension map of visibility properties,and the trajectories of satellites with circular orbits and repeating ground tracks are converted to several inclined lines in the map.By analyzing the intersections of the lines and the edge of the coverage region,the coverage durations for the ground point can be calculated.Based on the point coverage,the variations of coverage characteristics along the parallel are analyzed, and the regional or global coverage characteristics of constellations can be obtained. Numerical examples show that the proposed method can accurately and rapidly calculate the coverage characteristics,e.g.revisit time and coverage time.The calculated results are extremely close to those of the Satellite Tool Kit(STK)and are also superior to the existing research results.The proposed analytical model can be a useful tool for constellation design and coverage performance analysis.

1. Introduction

Earth coverage calculation is the basic issue for satellite constellation design and performance analysis.1-4Usually,coverage problems can be divided into two parts, including the continuous one and the discontinuous one.5-7For the continuous coverage, an arbitrary point on the globe or parallel can be covered by at least one satellite at any moment; while for the discontinuous one, the point is covered intermittently.Extensive research for the continuous coverage analysis has been carried out in the last few decades, and some valuable results such as Streets of Coverage (SOC) and Walker’s method have been widely used.8,9However,due to the increasing application of the Low Earth Orbit(LEO)satellite constellation, the discontinuous coverage has gradually received considerable critical attention.10-12

Investigators have often emphasized the complexity of the discontinuous coverage problem.13-19There are several differences between continuous and discontinuous coverage.Firstly, the Earth rotation does not influence the continuous coverage and is not considered for solving this problem, while it can directly affect the discontinuous coverage, and hence the analysis of the complex Spatio-temporal relationship between satellites and Earth turns to be necessary. Secondly,the continuous coverage can be calculated on a stationary unit sphere without any error in coverage characteristics,while for the discontinuous one, the specific altitude of the satellite needs to be considered. Thirdly, the precession of the orbit is not considered in the continuous coverage, yet it must be taken into account for the discontinuous one. A specific summary of the above-mentioned differences can be found in Ref.11. As a result, the methods for the continuous coverage analysis are no longer applicable, and new methods for calculating the discontinuous coverage need to be developed.

The most widely used method for calculating discontinuous coverage is grid analysis (direct modeling or simulation).11,20With a given time interval, a time step, some satellites,and some ground points, the relative positional relationships between the satellites and the ground points can be analyzed in each step through simulation, and the coverage characteristics during the whole time interval can be obtained. Plenty of research has applied this method for constellation design and coverage performance analysis.18-27However, the direct computation is quite time-consuming, and the accuracy of the coverage calculation highly depends on the number of the selected ground points, the time interval, and the time step. Some studie focus on the optimal choice of the ground points,24,25yet it still takes a lot of time to evaluate the regional or global coverage performance of a constellation.As for the analytic methods for coverage calculation, Ulybyshev6,18presented a geometric analysis method for discontinuous coverage. In his research, coverage region and two-dimensional map for visibility properties are introduced,and some typical orbital structures (Walker, or SOC constellations) are analyzed. However, due to the large allowable value of revisit time (larger than one orbital period) and low calculation accuracy, the ractical application of this method is partly limited. Razoumny11,28-30proposed the route theory of satellite constellation design for Earth discontinuous coverage. By analyzing satellites’ swath, as well as the intersections of satellites’ repeating ground tracks and parallels, the variations of coverage characteristics along the parallel are obtained. A high computing speed and wide applicable method for discontinuous coverage calculation is presented in the research. Nevertheless, the method ignored the duration of satellite visibility zones, which indicates that computed revisit time is not accurate enough, and also the coverage time cannot be calculated. Besides, Crisp23introduced a semi-analytical method for calculating revisit time.By calculating the longitude of successive passes and determining the visible time in a given duration, the revisit time of a given ground point can be obtained. However, their research can only deal with the symmetrical constellations(e.g. walker constellation) and the given ground points,and the variation of coverage characteristics along parallel is not revealed, wherefore the method is partly limited in use.

To overcome the shortcomings of the previous research,an analytical model for calculating the Earth discontinuous coverage of satellite constellation with repeating ground tracks is presented in this paper. The application of coverage region and route theory11are combined and extended in the analytical model. Specifically, the visibility condition for a ground point is represented as a coverage region in the twodimension map of visibility properties, and the trajectories of satellites with circular orbit and the repeating ground track are converted to several inclined lines in the map.By analyzing the intersections of the lines and the edge of the coverage region, coverage durations for the ground point can be calculated. Based on the point coverage, variations of the coverage characteristics along parallel are analyzed,and the regional or global coverage characteristics of satellite constellations can be obtained. The presented method can accurately and rapidly calculate the point,parallel,regional,or global coverage characteristics, e.g. revisit time and coverage time. In particular,compared with the route theory, the calculation accuracy can be highly improved, and the type of the calculated coverage characteristics can also be increased, without sacrificing the calculation time. The proposed analytical model can be a useful tool for constellation design and coverage performance analysis.

The rest of this paper is organized as follows:Basic mathematical models are described in Section 2. The coverage analysis of a single satellite is presented in Section 3.The coverage analysis of a constellation is proposed in Section 4.Simulation results and comparisons are given in Section 5.Finally,conclusions are presented in Section 6.

2. Basic mathematic models

Basic mathematic models are presented in this section, including repeating ground track orbit, Satellite coverage geometry,and coverage region.

2.1. Repeating ground track orbit

In this study, repeating ground track and circular orbit are considered, and the orbital radius, as well as the inclination,are the same for all satellites in the constellation to be analyzed. The purpose of the above settings is to ensure that the coverage sequence for an arbitrary ground point can be repeated within one repetition period, and also to obtain a stable analytic solution for discontinuous coverage.

A ground track is considered as repeating or periodic if it repeats at a fixed time interval allowing a cyclic observation of the Earth.31Let Tpbe the nodal period of the satellite orbit,npbe the corresponding angular velocity, and Tdbe the nodal day. Then for the repeating ground track orbit, it should be guaranteed that the period Tpprecisely matches the period Td, and this can be described as a mathematical condition,which is the following expression

where Tris a fixed time interval, which is also the period of repetition. m and n are two positive integers that are prime to one another, and m/n is defined as the repetition factor.

Actually,for an arbitrary orbit,let r-be the radius and i-be the inclination.Then,a repetition factor m/n can be found for the repeating ground track orbit defined by the inclination i= i-and the radius r being arbitrarily close to r- with any pre-assigned accuracy.11However, there is a one-to-one matching between the orbit radius and the inclination when the repetition factor is given,and also,the choices of the orbits with short repetition period,as well as small m and n,are quite limited.31As a result, an arbitrary orbit radius and an arbitrary orbit inclination would usually lead to a large m and n,as well as a long repetition period Tr, which might also be the so-called non-repeating orbit (orbit with a super long repetition period).

An example of these nodes mentioned above is presented in Fig.1,where the repetition factor is 5/1,points A1to A5denote the ascending latitudinal nodes, points D1to D5denote the descending latitudinal nodes, and points V1to V5denote the vertex nodes.

2.2. Satellite coverage geometry

Swath captures on the lower parallel are illustrated in Fig.4,where A denotes the ascending node,ALis the westernmost point of the captures on the parallel, and ARis the easternmost point.

The longitudinal distance between the point ALand A represents the left side capture αL, and the longitudinal distance between the point ARand A represents the right side capture αR. Let u be the Argument of Latitude (AOL) corresponding to the ascending node A. Then, specific expressions of the one side captures are as follows11and sign(x ) is a unit function, which returns 1 when x ≥0,and returns -1 when x ＜0.

2.3. Coverage region

Coverage region is first proposed by C. Wilkinson, and the function is to show the mutual visibility between a circular orbit satellite and a ground point.34There are mainly two types of coverage regions, which are exactly corresponding to the lower and upper latitudes mentioned above. For the upper latitude, there are three subtypes, including normal upper latitude, polar cap, and equatorial loop. These categories are introduced in Ref.34and can be shown in Fig. 5,

where point P denotes the North Pole,and the grey circle represents the coverage region of a ground point at latitude φ. It should be mentioned that the coverage region is different from the satellite’s instantaneous coverage area, and the ground point can be covered by a satellite when the Sub-Satellite Point(SSP) falls in the coverage region. In Fig. 5, for the lower latitude(within),the coverage region is completely within the latitude limit |φ |≤i0; for the normal upper latitude (single intersection),a part of the coverage region is out of the latitude limit; for the polar cap (encompasses), the coverage region encompasses the north or the south polar region out of the latitude limit; for the Equatorial loop (double intersection), two parts of the coverage region are out of the latitude limit.

In order to make better use of the coverage region,scholars have carried out some transitions and presented the coverage region in a two-dimension map,of which the x-axis represents the RAAN of a satellite,and the y-axis represents the AOL.34-36The coverage region in the two-dimension map can be one or two independent closed areas, and each ground point has its own coverage region. If the RAAN and AOL of one satellite belong to the coverage region,then the ground point is visible for the satellite. Specific mathematic descriptions of these coverage regions are as follows.

(1)Lower latitude,the latitude that satisfies φ| |＜i0-θL.A parallel can be covered twice a revolution, and the coverage region is two independent areas in the two-dimension map.

(2) Normal upper latitude, the latitude that satisfies i0-θL≤|φ |≤i0+θU, and |φ |≤π-i0-θUwhen i0+θU＞π/2. A parallel can be covered once a revolution,and the coverage region is one independent area in the twodimension map.

(3) Polar cap, the latitude that satisfies i0-θL≤|φ |≤i0+θU, |φ |＞π-i0-θUand also i0+θU＞π/2. A parallel can be covered once in each revolution, and the coverage region will be distributed along the entire x-axis of the two-dimension map.

(4) Equatorial loop, the latitude that satisfies i0-θL≤|φ |≤i0+θU, |φ |＜θL-i0and also i0＜θL.A parallel can be covered once in each revolution, and the coverage region will be distributed along both the entire x-axis and the y-axis of the two-dimension map.

Specific examples of the coverage region mentioned above are presented in Fig. 6, where the black point in the middle of the coverage region represents the satellite that is directly above (when |φ |≤i0) or closest to (when |φ |＞i0) the ground point during the ascending or descending pass, and is defined as the middle point of the coverage region.

3. Single satellite coverage analysis

Coverage by a single satellite is analyzed in this section,including point coverage and parallel coverage.Coverage region and two-dimension map are employed for the analysis, while still,we need a little trick to improve the expression of the map.

The two-dimension map is traditionally defined in inertial space with the x-axis denotes RAAN and the y-axis denotes AOL.6For a specific ground point,the coverage region moves along the x-axis at a speed of ωE(angular speed is considered here since the unit of the axis is rad).For the satellite, the trajectory in the map is a line that is slightly inclined to the y-axis due to the perturbation.The satellite moves along the line with a speed of ˙Ω in the x-axis direction and a speed of npin the yaxis direction, as shown in Fig. 7.

Here we use a little trick to make the analysis more distinct and convenient. Consider the relative motion between the satellite and the coverage region, and fix the coverage region in the map. Then the movement of the satellite would turn to be several inclined lines in the map, and the meaning of the x-axis becomes the Longitude of Ascending Node(LAN), as presented in Fig. 8.

It’s obvious that the number of the inclined lines in the map is exactly m(which is also the number of the revolutions in one repetition period),and the lines are defined as satellite tracks in this study. The distance between the adjacent tracks in the xaxis direction is equal to ΔL,which is in coincidence with that concluded at the end of Subsection 2.1. Also, it is easy to obtain the slope of these inclined tracks, which is marked as ksatand can be expressed as

Therefore, the two-dimension map is converted to an improved one defined in the Earth fixed system,and the coverage duration is defined as the section where the satellite track intersects the coverage region.

3.1. Point coverage by a single satellite

Thus,the specific position of the coverage region in the map can be determined by TRand TL. For the upper latitude, the middle point can also be obtained by substituting φ=i0in Eq. (17).

The satellite tracks are numbered as 1 to m,where the number 1 represents the track where the satellite located at the initial time,and the numbering order is from right to left.Define the intersections of the tracks and the x-axis as λs,where s varies from 1 to m at intervals of 1, and can be marked as s=1(1 )m. In such kind of formulation, the two numbers beside the parenthesis represent the lower and upper bounds respectively, and the number inside the parenthesis represents the interval,the same below.Then the intersection of the initial track (s=1) can be expressed as

As a result, positions for all the intersections can be determined,since the distance between the adjacent tracks in the xaxis direction is equal to ΔL.

Also, the time relationship of different tracks needs to be determined. Let τ1=0 be the satellite’s passage time for the first intersection λ1, which is also the initial time of the coverage duration,and then the passage time for other intersections must be an integral multiple of the nodal period Tp,which can be defined as

where k is a minimal nonnegative integer for which asis an integer.

Once the locations of the coverage region and the tracks are determined, and the passage time for each track is obtained,the next task is to calculate the intersections of the tracks and the coverage region, so as to obtain the specific coverage

It can be seen from the calculation that the more the number of points on the region edge, the more accurate the calculation for the intersection, and the lower the calculation efficiency. Thus, the number of points on the edge can be determined according to the specific requirements of calculation efficiency and accuracy.

Other coverage characteristics such as mean revisit time can also be obtained by the coverage sequence.

3.2. Parallel coverage by a single satellite

Parallel coverage by a single satellite is analyzed in this subsection. Different from the point coverage, we aim to find the change law of the coverage characteristics along the parallel,which is also analyzed in the route theory proposed in Ref.11. We considered the coverage region and extended the route theory, and present a new and superior method.

As the ground point moves along the parallel, the corresponding coverage region would move along the x-axis in the map. It is obvious that after moving the length of ΔL,the position relationship between the satellite’s tracks and the coverage region in the map is repeated, and the coverage characteristics for the ground point can also be repeated.Thus,the whole parallel can be represented by the arc in the length of ΔL,which is defined as a typical segment in this study.On the other hand, with the movement of the ground point on the parallel, the coverage time varies gradually, while the revisit time may change rapidly since the change of the intersections of the tracks and the coverage region is discontinuous. Therefore,the coverage characteristics along the parallel can be classified according to the change of the revisit time.

Assume that the coverage region moves forward along the x-axis, and the length of the movement is ΔL, then, the relationship between the left or right edge coverage region and the tracks can be analyzed.As illustrated in Fig.11,the curves in Fig. 11 (a) represent the right edge of the coverage region,and the curves in Fig.11(b)represent the left edge of the coverage region. Obviously, as the coverage region moves, the right edge will intersect a new track that is out of the coverage region, and the left edge will leave a track that is in the coverage region.

The classification of the coverage characteristics along the lower latitude parallel is carried out firstly. The coverage region of a point with lower latitude is divided into two independent parts,and each part has its right and left edge.Therefore, there can be four different coverage situations for the intersection of the satellite’s tracks and the coverage region,which can be described as follows.

(A) The right edge of the right part of the coverage region intersects a track.

(B) The right edge of the left part of the coverage region intersects a track.

(C) The left edge of the right part of the coverage region leaves a track.

(D) The left edge of the left part of the coverage region leaves a track.

An example of the above four situations is given in Fig.12,

where the bold tracks represent the tracks that intersect the coverage region.

The order of the coverage situations mentioned above is not fixed,yet it is related to the specific latitude.Also,the length of some situations in the typical segment might be zero;for example,situations(A)and(B)appear on the same ground point at the same time.In each situation,the revisit time varies slightly,so the coverage for one point in the situation is enough to represent the whole situation.

For the normal upper latitude, only situations (A) and (D)exist; for the polar cap or equatorial loop, the coverage characteristics change slightly along the whole parallel, and thus only one coverage situation exists.Define all possible coverage situations on a typical segment as coverage variants, then for all coverage variants, the intersections of the tracks and the coverage region are different from each other, e.g. situation(a) to (d) for the lower latitude coverage of one satellite. Let χ be the number of coverage variants on the typical segment,then, for the parallel coverage of one satellite, the value of χ can be 4 for lower latitude, 2 for normal upper latitude, or 1 for polar cap and equatorial loop, and this is also consistent with the route theory concluded in11.

Once the coverage variants are determined, the next task is to calculate the length of each variant,and calculate the specific intersections of the track and the coverage region, so as to obtain the parallel coverage characteristics. Considering the tracks that are tangent to the left and right edge of the coverage region and also the tracks that directly pass overhead the ground point,the relationship of these tracks can be expressed as Fig.13,where αLand αRare the coverage captures given by Eqs.(12)and(13),and Δψ denotes the x coordinate difference between two middle points in the coverage region. Δψ can be obtained based on the slope of the track and the coordinates of the two points given by Eqs. (16) and (17), and the specific expression is

Based on the coverage captures,the length of each coverage variant can be analyzed.As illustrated in Fig.14,let Nmbe the maximum number of the tracks that can intersect the left or right part of the coverage region at the same time, and then Nmcan be expressed as

where the function floor(x) returns the maximum integer not exceeding x. In Fig. 14, we have Nm= 2.

After containing Nmtracks,the maximum remainder of one part of the coverage region, which is marked as Lm, can be defined as

The relationship between the tracks and the coverage region is analyzed by numbering each track in the twodimension map. Starting from the coverage situation (A), let the track tangents to the right edge of the right part of the coverage region be the first numbered track, of which the sign is the number ‘‘1”, as presented above the track in Fig. 14. Let p be the sign of the track that first intersects the right edge of the left part of the coverage region, and Lpbe the xcoordinate difference between the track p and the track tangent to the right edge of the left part of the coverage region in the coverage situation (A), as shown in Fig. 14. Then, p can be expressed as

Let Nabe the number of the tracks that intersect the left part of the coverage region,q be the sign of the leftmost track that intersects the left part of the coverage region, and Lqbe the x coordinate difference between the track q and the track tangent to the right edge of the left part of the coverage region in the coverage situation (A), as illustrated in Fig. 14. Then,there are two cases for the value of Na.Case 1:Lp≤Lm.In this case,there are also Nmtracks that intersect the left part of the coverage region,and hence Na= nm.The number of the tracks that intersect the left edge of the left part of the coverage region is q=p+Nm, and the distance Lqcan be defined as Lq=Lm-Lp. Case 2: Lp＞Lm. In this case, there are Nm-1 tracks that intersect the left part of the coverage region,and hence Na= nm-1.The number of the tracks that intersect the left edge of the left part of the coverage region is q=p+Nm-1, and the distance Lqcan be defined as Lq=Lm-Lp+ΔL. In Fig. 14, we have Na= Nm-1=1.

As the coverage region moves along the x-axis,the remaining situations(B)to(D)may appear,and specific lengths of the movement of the coverage region for the appearing of these situations need to be determined,which are marked as L1,L2and L3. As presented in Fig. 14, these lengths can be expressed as

Let lνbe the length of each coverage variant, where ν=1(1 )χ. Let NRand NLbe the number of tracks that intersect the right and left part of the coverage region,and let pLbe the sign of the first track that first intersects the right edge of the left part of the coverage region. Then the abovementioned parameters are enough for the point coverage analysis in each variant. As the size relationship between L1, L2and L3changes, the values of lν, NR, NLand pLare different.Let the number 123 represent the case that L1≤L2≤L3, and number 132 represent the case that L1≤L3≤L2, and so on.Then, the specific parameter values for the lower latitude can be listed in Table 1.

For the normal upper latitude, only two coverage variants exist on the typical segment, as presented in Fig. 15. Since αLand αRare given by the Eq. (15), Nmand Lmcan also be obtained by Eqs. (26) and (27). The length lνof each variant,as well as the number of tracks that intersect the coverage region in each variant, can be listed in Table 2.

For the polar cap or the equatorial loop,the number of the coverage variant is 1, and the number of tracks that intersect the coverage region is m.

Therefore,for the coverage by one satellite for an arbitrary parallel, the coverage variants on the typical segment can be obtained by the above analysis, and the specific parameters of the intersections of the tracks and the coverage region in each variant can be determined.Also,in each variant,coverage analysis for one point is enough to represent the whole variant.Thus,at least one point in each variant(4,2,or 1 points on the parallel in total) is required to reveal the change of the coverage characteristics along the parallel, and the problem of parallel coverage by one satellite can be consequently converted to several point coverage problems, of which the specific method is presented in Section 3.1.

4. Constellation coverage analysis

Coverage by constellation is analyzed in this section,including point coverage, parallel coverage, as well as regional and global coverage.

4.1. Point coverage by a constellation

Point coverage by constellation can be analyzed by combining the coverage of each satellite in the constellation. The same method mentioned in subsection 3.1 can be carried out, and the coverage durations in one repeating period for each satellite in the constellation can be obtained. Thus, the coverage characteristics can be obtained through the combination of these coverage durations.

where ukrepresents the AOL of the kth satellite.

In addition, it should be noted that for each satellite, the coverage durations need to be limited to one repetition period.Also, the overlap of the coverage durations of each satellite ought to be considered,and the head and tail of each coverage sequence should be combined, so as to obtain accurate coverage or revisit durations. A simple example is illustrated in Fig. 16, where the bold line segments denote the coverage durations of each satellite.

Therefore,the coverage sequence CPof the constellation for one ground point can be expressed as

4.2. Parallel coverage by a constellation

Parallel coverage by constellation can be analyzed based on Subsection 3.2.As mentioned above,there are χ coverage variants on the parallel for the coverage by one satellite, where χ=4 for the lower latitude and χ=2 or 1 for the upper latitude. For the constellation with N satellites, there can be atmost χN coverage variants on the parallel due to different relative positions of each satellite. The main task is to obtain the coverage characteristics of each coverage variant on the parallel.

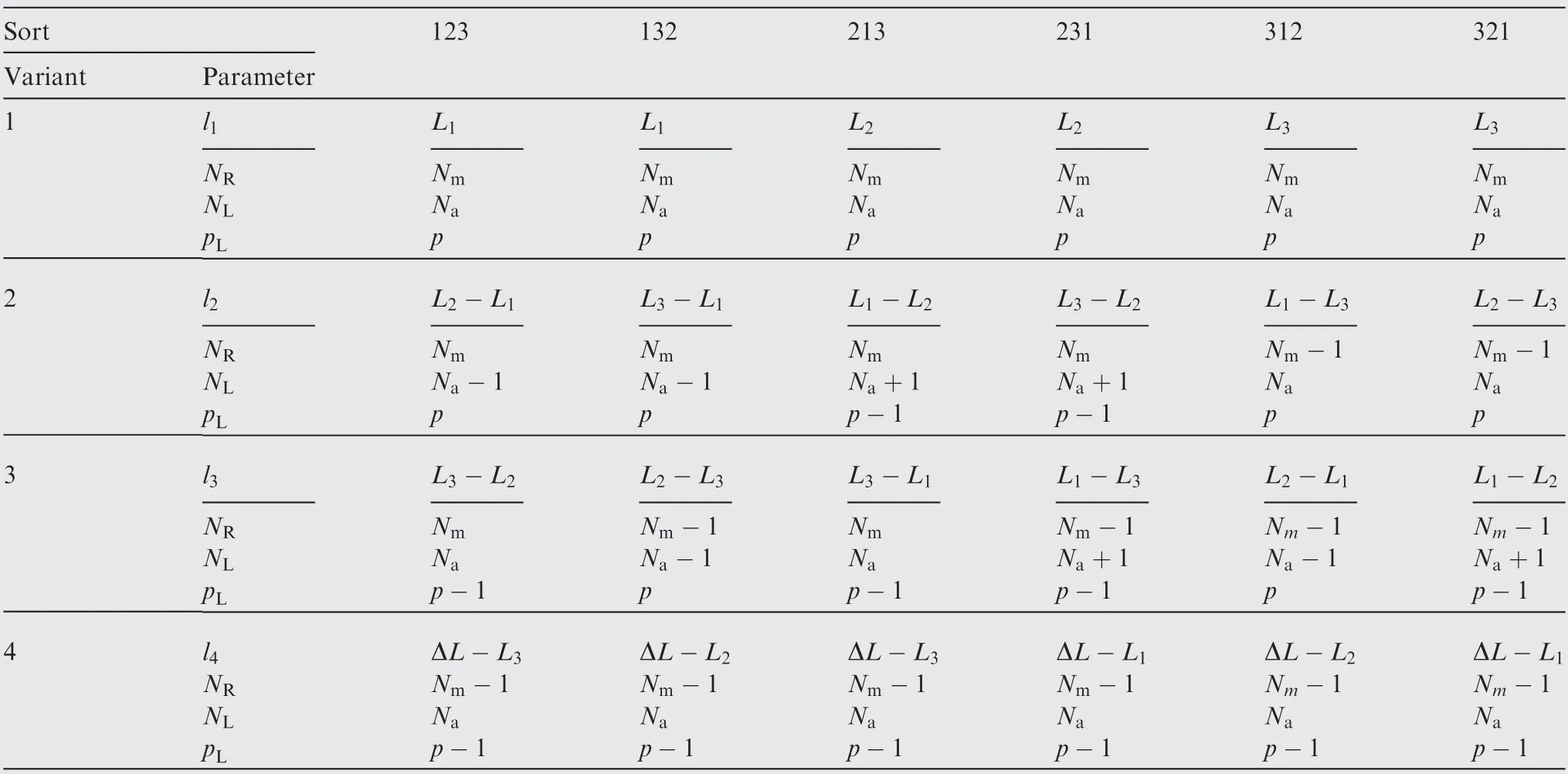
Table 1 Parameter values of each coverage variant for lower latitude.

Table 2 Parameter values of each coverage variant for normal upper latitude.

Let Ωkand ukbe the RAAN and the AOL of the kth satellite in the constellation, where k=1(1 )N, then, the first intersection of the track and the equator for the kth satellite can be expressed as

After obtaining χN new coverage variants on the typical segment, the coverage characteristics can be obtained by analyzing the coverage for the midpoint of each coverage variant.Let s′′rbe the midpoint of the rth coverage variant, where r=1(1 )χN, then we have

Thus, the coverage sequence of the kth satellite for the rth coverage variant can be obtained through the abovementioned four processes, and the method for combining the coverage sequence of each satellite is the same as that mentioned in Section 4.1. As a result, the coverage sequence Crof the whole satellite for the rth coverage variant can be expressed as

Also,the coverage characteristics,such as the revisit time or the coverage time,can be consequently obtained by the coverage sequence.

In summary, for the parallel coverage by constellation, at most χN coverage variants can be obtained,and each coverage variant can be solved by the above-mentioned method.

4.3. Regional and global coverage analysis

Regional and global coverage can be analyzed based on the parallel coverage mentioned above. The main idea is to divide the region or globe by some parallels, and thus the coverage characteristics can be obtained by analyzing these parallels.

For the regional coverage, the analysis is carried out by dividing the region into some arcs(each arc is a part of the parallel).For each arc on the parallel,it is composed of several or a part of the typical segment,and each typical segment consists of several coverage variants. Therefore, the coverage characteristics of each arc can be analyzed, and the coverage characteristics for the whole region can be obtained.

Other regional coverage characteristics can be obtained in a similar way.

As for the global coverage,the same analysis can be carried out. Let φmax∈[0,π/2] be the maximum latitude that can be covered by the constellation, and then the global coverage can be obtained by analyzing the parallels of which the latitude is between -φmaxand φmax.

5. Numerical results

Numerical results are presented in this section.Point coverage and global coverage are analyzed,and the results of this study,the results presented in existing literature,as well as the results obtained by STK,are compared together.For the point coverage, the MRT and the coverage time are calculated, and the results are verified by the STK. For the global coverage, the MRT is calculated and compared with the existing literature.

5.1. Point coverage

Point coverage by constellation is considered in this subsection. Parameters of the constellation, coverage and ground point are given as follows.

Walker constellation is introduced,of which the configuration parameters can be defined as N/P/F,where N denotes the total number of satellites,P denotes the number of orbits,and F is the phasing parameter.9,37Two configurations,which are 3/3/1 and 10/10/8, are considered for the analysis. The initial parameters of the satellite orbit in the constellation are listed in Table 3.

For the coverage parameter,the sensor type of each satellite is a simple conic,and the cone half-angle is 65 degrees.For the ground point,the longitude of each point is 0,and the latitude varies from 0 to 55 in the step of 5 degrees, which means 12 points are considered in total.

The initial time is set as 2021/01/01 00:00:00.0 UTC, and the scenario interval in STK is set as two repetition periods to avoid missing any possible revisit duration. The RAAN and the AOL of the anchor satellite in the constellation at the initial time are both 0,the coordinate system of each satellite is set as True of Date, and the propagation mode of the orbit is set as J2 perturbation in the STK.Results comparison is presented as follows.

(1) Configuration 3/3/1

The MRT and the coverage time(%)for each ground point are presented in Fig. 20 and Fig. 21, respectively, where the x-axis represents the latitude of each point, and the second y-axis on the right side represents the deviation of the results obtained by the proposed method (named as Proposed) and the STK.

As can be seen, the calculation of the MRT by the presented method is of high accuracy, of which the maximum deviation is less than 1.5 s. Also, the coverage time (%) for each point calculated by the presented method is consistent with that obtained by the STK, and the maximum deviation is less than 0.003 (about 2.6 s).

(2) Configuration 10/10/8

To further verify the presented method, point coverage by the 10/10/8 walker constellation is analyzed. The MRT and the coverage time (%) for each ground point are presented in Fig.22 and Fig.23,respectively,where the x-axis representsthe latitude of each point, and the second y-axis on the right side represents the deviation of the results obtained by the presented method and the STK.

Table 3 Parameters of satellite orbit.

As presented above,the maximum deviation of the MRT is less than 2.0 s, and the maximum deviation of the coverage time is less than 0.012 (about 10.2 s), which can also verify the accuracy of the presented method. Another notable result is that the maximum deviation of the coverage time is larger than that in the first case(configuration 3/3/1).This is because that there are more satellites in this case, and more intersections of the tracks and coverage region, along with more coverage durations.Thus,the deviation may become larger due to the accumulation. However, this is still a small deviation(about 1 s per satellite)and can be ignored in the coverage performance analysis.

5.2. Global coverage

To demonstrate the superiority of the presented method, global coverage by constellation is considered in this subsection.The parameters of constellation and coverage are set according to Ref.28, Table 2. In the reference, MRT of the global coverage of different Walker constellations is analyzed, and the results obtained by different methods are compared. In this study, the same constellations for global coverage are considered, and the MRT of each constellation is also calculated by analyzing different parallels on the globe at an interval of one degree.Specific results are listed in Table 4,where the last column of the MRT is obtained by the method presented in this paper. Besides, the calculation times of the presented method are also presented in the last column of Table 4. The C++ language is used for programming, and the calculation is implemented on the laptop with an Intel Core i7-1065G7 1.30 GHz processor.

From the table,we can find that the results of this study are extremely close to those of the STK and the Lang,and the calculation accuracy of the presented method is much higher than that of Razoumny’s method.28In particular, for Razoumny’s method, since the duration of satellite visibility zones is ignored, the larger the visibility zones, the larger the calculation deviation, yet this won’t appear in the presented method.Also,the calculation time of the presented method for the global coverage of one constellation is only a few seconds, and most of which are less than one second, which is close to that of Razoumny’s method. Thus, the proposed method can achieve a higher accuracy without sacrificing computational efficiency.

Another notable result in Table 4 is that for the configuration 5/5/4,the MRT obtained by the STK is completely different from that obtained by other methods. Specific reasons are presented as follows.For the walker constellation 5/5/4 with a repetition factor 241/18, the length of the typical segment is only about 1.49 degrees, and for the lower latitude, there are 4×5=20 coverage variants in one typical segment. Thus,the length of each variant can be quite short.By analyzing different parallels, we can find that the global MRT appears on the parallel of which the latitude is about 12 degrees. The distribution of the MRT on the typical segment of this parallel is presented in Fig. 24.

From the figure, we can find that the MRT for most coverage variants on the parallel is about 120 minutes, while the MRT for a few coverage variants is about 224 minutes, and the length of these variants is so short that they cannot be discovered by merely setting few points on the parallel. Hence, if the number of the ground point on the parallel is not dense enough, the global MRT will be definitely ignored. To verify the above statement, we set 100 ground points on the parallel in the STK, and the result shows that the MRT is about 224.15 minutes, which is consistent with the result obtained by the presented method. Therefore, the presented method can find all possible coverage characteristics effectively, which is much superior to the direct simulation method where the global coverage is represented by the coverage for some ground points.

6. Conclusions

In this paper,an analytical model for calculating the Earth discontinuous coverage of satellite constellation with repeating ground tracks is proposed.The application of coverage region and route theory are integrated and extended,and methods for analyzing point, parallel, regional as well as global coverage are successfully designed.

Numerical examples show that the proposed analytical method can accurately and rapidly calculate the coverage characteristics, e.g. revisit time and coverage time. On one hand,point coverage by constellations is analyzed, and the results are extremely close to those of the STK.In particular,the maximum deviation of the MRT is less than few seconds, and themaximum deviation of the coverage time is about 1 second per satellite. On the other hand, the change law of the coverage characteristics along the parallel is revealed, and thus the regional or global coverage can be calculated accurately and comprehensively. Results show that the global MRT calculated by the presented method is consistent with that of the STK, and also, comparing to the existing studies, the calculation accuracy can be highly improved, and the type of the calculated coverage characteristics can also be increased,without sacrificing the calculation time.

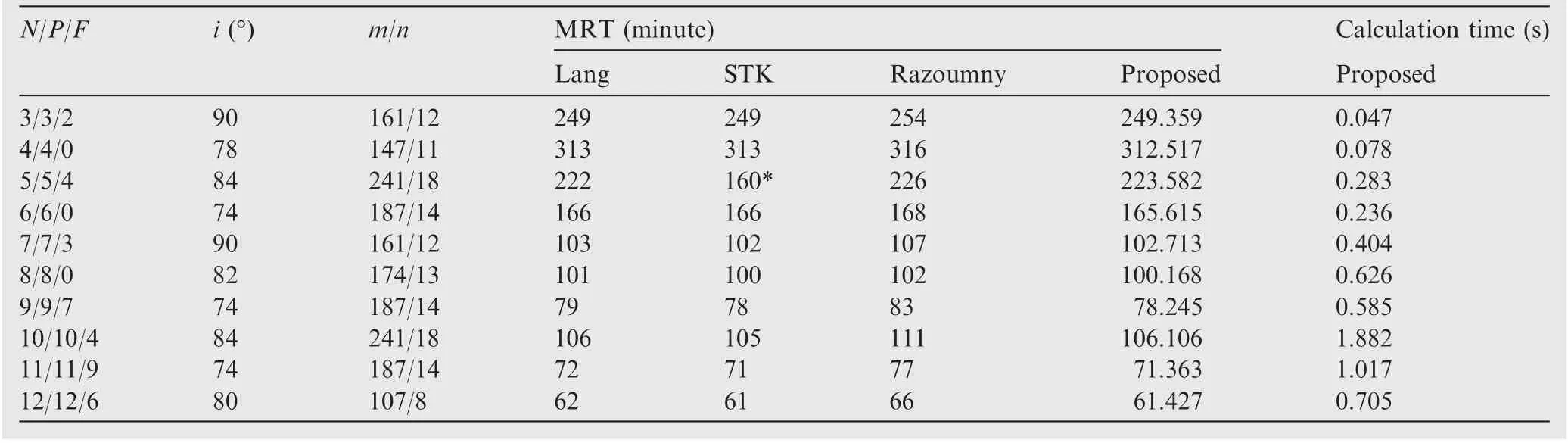
Table 4 MRT values of Walker constellations calculated by different methods.

Furthermore, it should be mentioned that the presented method can be applied to any circular orbit satellite since an arbitrary orbit radius and inclination can be expressed by a repetition factor with any pre-assigned accuracy. However,this would usually lead to a long repetition period, which means that the coverage characteristics may need a long time to become stable. Therefore, the choice of the orbit radius and inclination depends on the specific requirement of the designer. If stable coverage characteristics in a short duration are demanded, it’s better to choose the orbit with a short repetition period. The proposed analytical model can be a useful tool for constellation design and coverage performance analysis.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This study was co-supported by the National Natural Science Foundation of China (No. 12072365) and the Hunan Provincial Natural Science Foundation of China (No. 2020JJ4657).