Neural Network aided PMSM multi-objective design and optimization for more-electric aircraft applications

Yun GAO, To YANG,*, Serhiy BOZHKO, Pt WHEELER,Tomislv DRAGICEVIC, Chris GERADA

a Power Electronics, Machines and Control Group, University of Nottingham, Nottingham NG7 2RD, UK

b Department of Electrical Engineering, Technical University of Denmark, Kgs. Lyngby 2800, Denmark

KEYWORDS Design and optimization;Loss estimation;Mean Length per Turn(MLT);More-Electric Aircraft(MEA);Neural Network (NN);Permanent Magnet Synchronous Motor (PMSM)

Abstract This study uses the Neural Network (NN) technique to optimize design of surfacemounted Permanent Magnet Synchronous Motors (PMSMs) for More-Electric Aircraft (MEA)applications.The key role of NN is to provide dedicated correction factors for the analytical PMSM mass and loss estimation within the entire design space.Based on that,a globally optimal design can be quickly obtained.Matching the analytical estimation with Finite-Element Analysis(FEA)is the main research target of training the NN.Conventional analytical formulae serve as the basis of this study,but they are prone to loss accuracy(especially for a large design space)due to their assumptions and simplifications.With the help of the trained NNs,the analytical motor model can give an estimation as accurate as the FEA but with super less time during the optimization process. The Average Correction Factor(ACF)approach is regarded as the comparison method to demonstrate the excellent performance of the proposed NN model.Furthermore,a NN aided three-stage-sevenstep optimization methodology is proposed.Finally,a Pole-10-Slot-12 PMSM case study is given to demonstrate the feasibility and gain of the NN aided multi-objective optimization approach.In this case, the NN aided analytical model can generate one motor design in 0.04 s while it takes more than 1 min for the used FEA model.

1. Introduction

In recent decades, the continued progress of Permanent Magnet Synchronous Motors (PMSMs) development has led to a situation that they are widely used in electrical vehicles, fans,drives, and compressors.1-7PMSM is commonly selected for electromechanical actuators in the More-Electric Aircraft(MEA) due to its high power density, reliability and efficiency.3,8-11Moreover, a few literatures have shown the suitability of PMSMs for different MEA generation and environmental control systems.11-13However, the problem of designing an optimal PMSM is still challenging because of its multi-physics nature. Several computational models can account for the multi-physics design, including the closedform analytical model, lumped parameter model, Finite-Element Analysis (FEA) model, combined finite-element, etc.Among that, FEA models are the most current but also most time consuming. Therefore, time-step FEA can be a practical tool to verify the machine performance based on simpler analytical models since it is impossible to verify all analytical estimations with experiments.4,14,15Due to that,FEA has become the main approach to design and optimize PMSM also the basis of manufacturing the benchmark system.This paper proposes to use a nonlinear surrogate model, Neural Network(NN), to correct the PMSM analytical estimated performance based on the samples from FEA, which is a very efficient way for speeding up the FEA-based PMSM optimization.16,17

Two objectives of PMSM optimization are studied in this paper: total mass (M) and total power loss (PL). For the PMSM mass, which is critical for MEA applications, it can be estimated with relatively high accuracy because the motor geometries and materials are usually parameterized and they can be confirmed for a potential motor design based on a fixed topology.1,2,8,9Further improving the mass estimation requires a more accurate winding weight estimation, since the winding is the most uncertain part in mass estimation. The winding length is related with a few factors (e.g. winding type, number of turns, end winding), while only the Mean Length per Turn(MLT) can be tuned in the analytical approach.2,8The PL is much more difficult to estimate compared to the total mass M. This is due to the fact the flux field is coupled with quite a lot of factors and flux density varies much among backiron, tooth, Permanent Magnet (PM) and rotor. In that case,the analytical method is prone to lose its accuracy since traditionally only the flux density of typical points is utilized instead of considering the whole PMSM area.To solve these problems in mass/loss estimation, this work reported in this paper utilizes the NN aided approach to bridge the gap between the analytical methods and FEA in the whole design space.Based on that, the optimal PMSM design with multiple objectives can be quickly and globally found in this space.

Many analytical and FEA methods of PMSM design and optimization have been studied in literatures.A fast,accurate,and high dimensional multi-physics analytical model for PMSM was presented in Ref. 2 with the FEA and experimental validation on typical design points. The resulting model takes an average of 0.03 s to run on a standard PC. Based on that, the system-level optimization of a motor drive design is studied in Ref. 7 by using an advanced evolutionary optimization algorithm. Ref. 18 utilized the explorative particle swarm optimization to find the optimal design of a PMSM with a mesh adaptive direct search. Even though the authors declare that the proposed rule of start point selection takes an advantage of minimizing the search time, the proposed approach was not quantitatively compared with other search methods regarding the search and computation time. The shape optimization of PMSM was studied in Ref. 19 by using an analytical Kriging surrogate model (a statistical-based interpolation method) but, the FEA-based iteration should be done to get the convergence of the surrogate model which can cost a long computation time. In contrast, the proposed NN-aided approach only needs to evenly sample a small number of FEA-based design points (64 in the case study) for the NN training; after which, the analytical model can be corrected with very high accuracy in the entire design space.

Another approach to build a surrogate model for PMSM performance is building a response surface.16,20Using both the analytical and the FEA model, Ref. 20 has chosen the significant parameters for an additional optimization with a reduced simulation model. Based on that, a response surface model can be built analytically.However,one major disadvantage of the response surface model is that its approximation performance is always limited by the pre-chosen equation(e.g. polynomial, exponential). In contrast, NN is a general nonlinear surrogate model that can approximate any given input-output function with arbitrary precision.21,22Moreover,there is no need to specify the math relations between inputs and outputs of NN. Though NN modelling requires a certain additional time for collecting a small amount of sample data,this is justified by a much faster evaluation of PMSM designs in the NN execution stages.16

Up to now, the NN-aided PMSM design and optimization is still rarely reported. Ref. 17 utilized NN to build surrogates for machine optimization which has the best accuracy versus training time tradeoff among several surrogate candidates;however, most of the NN technical details (e.g. sample collection, NN training and test) are not given. In Ref. 23, NN was embedded into the FEA-based evolutionary optimization using Genetic Algorithm (GA)24,25to reduce the very high computational effort. However, as it depends on the detailed FEA models,it can thus still be time-consuming and probably much slower than the hybrid method of NN and analytical models in this paper.In addition,the application of GA would bring risk of getting stuck in local optimum.22,24An adaptive network-based fuzzy inference system was presented in Ref.26, this system acted as a surrogate for the motor FEA optimization. This approach may speed up the original FEAbased optimization but,the computation time for the proposed method was still quite long(around 24 h)in the case study and the actual time for the surrogate was nearly half an hour. In addition,the optimization block diagram(using the surrogate)was not clearly described. In Ref. 27, two NN architectures were proposed to quickly and accurately predict the motor torque and efficiency. For the training data collection, there are two FEA simulation stages: (A) flux linkage calculation; (B)torque and efficiency.And the exaction calculations using analytical equations are located between two FEA stages. Differently, this paper proposes a NN based correction model linking analytical models to the detailed FEA thus,the analytical model and the FEA model of PMSM are separately considered and there is no data transfer in between.

This work proposes the NN aided approach for both PMSM mass and loss correction. It utilizes simple conventional math equations and the trained NN,it is thus extremely fast with no need for substantial derivations. More importantly, NN based correction model can give dedicated factors to ensure the high accuracy of mass/loss estimation in the whole PMSM design space. Therefore, global optimization of PMSM can be obtained quickly and smoothly based on the simple analytical models and trained NNs. Lastly, the NN aided approach is independent to the PMSM topologies and sizing models because of the constraint-free surrogate function of NN; therefore, it is very easy to be generalized to other PMSM optimization problems for the aircraft application.

This paper is organized as follows: fundamental equations of mass/loss estimation are given in the next section where their limitations and comparisons with FEA are also discussed.The proposed NN approach for mass/loss correction is presented in Section 3; furthermore, Average Correction Factor(ACF)method is given as a comparison method,their comparison results in a PMSM case are depicted at the end of Section 3. In Section 4, the proposed NN aided global optimization procedure is introduced step-by-step. After that,a new PMSM case is studied in Section 5 for the method validation and the optimization method is compared with the conventional FEA-based optimization. Finally, this paper is concluded in Section 6.

2. Analytical estimation for mass and power loss

This section will discuss the limitations of the analytical mass and loss estimation methods. In general, these analytical(math) methods pursue the design efficiency thus usually depend on one or several design factors/coefficients, which would give a poor estimation performance for large design spaces though they can predict the performance close to FEA at certain design points. It is important to notice that the purpose of analytical models is to give the base data for the following NN training thus, the models provided here can be changed to any other feasible or desired motor models with no impacts on the method application.

The following subsections will introduce the mass and loss analytical estimations separately.

2.1. Mass estimation

As mentioned above, accurate estimation of winding mass is the most challenging part in PMSM because winding mass are dependent on quite a few parameters including material,end winding, number of turns etc. Therefore, this subsection mainly discusses the limitation of conventional analytical estimation approaches for winding mass.

Conventionally, MLT is utilized for analytically design of the motor winding based on the given number of turns, wire diameter and winding material.2,8,28,29As shown in Fig. 1(a),in Ref. 28, MLT is given as twice the sum of the stack length and the semicircle arc around the corner (named as ‘‘Method 1”). The equation is:

where Lstis the stack length of motor and D here represents the slot pitch to give the end-winding length(Lew).In practice,D is usually corrected with a coefficient Kew1depending on the actual Lewlength.Another MLT determination method can be referred to Ref.29 which also considers two contributions:the turn part embedded in the slot(Lcore,which equals Lst)and the end-winding (Lew), named as‘‘Method 2”.However, the computational equations are slightly different:

This paper proposes another MLT computational method to derive the Lewin Eq. (2), which utilizes the tooth width(Widto)and the bottom lengths of slot rather than the pole/slot pitch in above two methods. The proposed computational equation of Lewis:

where Kp,ewis the proposed end-winding coefficient, b1and b2are the lengths of slot upper/lower bottoms. In order to compare the estimation performance of these three MLT methods,two Design Variables (DVs), tooth base fraction and PM height, are chosen to give the comparative sensitivity analysis and,other motor parameters stay the same with the case study in Ref.15.First,a base design point in the 3D model of a software,MotorCAD,is given to derive the values of three coefficients: Kew1, Kew2, and Kp,ew. Namely, assume a motor design in MotorCAD and get the MLT value to inversely derive three coefficients by using above equations.

The base design and the updated coefficients can be found in Table 1. Two variables are tooth base fraction and PM height, the three coefficients are obtained by the base designof(0.6,4.4 mm)in MotorCAD.Then,evenly sample two DVs in a range (sampling rang and step of two variables can be found in Table 1) and further collect the MLT results of both the 3D model and three afore-mentioned methods.Lastly,calculate the errors between analytical methods and the 3D model. The error variation and comparison results are shown in Fig. 2.

Table 1 Key parameters and sampling range/step in MLT estimation studies.

The horizontal axis of Fig. 2(a) refers to the series number of the design points (circle/star marked) in Fig. 2(b). Obviously, Method 1 has the same estimation performance with Method 2 though they are using slightly different equations.In contrast, the proposed MLT method appears a totally different variation direction with the other two methods. However, as shown in Fig. 2(b), there is no best analytical method for MLT estimation in the given ranges of two DVs.The proposed method can give closer estimation than Method 1&2 when using the blue-star design points but loses the priority for the red-circle designs.

In summary, neither the proposed MLT method nor Method 1&2 can consistently provide the highly accurate estimation in the design space.The key reason comes from the fact that three coefficients (Kew1, Kew2, and Kp,ew) all stay unchanged in the design space and are thus not adaptive against the DV changes. To this end, this paper proposes the NN aided approach to correct the motor total mass estimation, which can guarantee the high accuracy with regards to DV changes in a certain design space.

It is important to note that winding length is also significant in loss estimation as it directly determines the motor dc resistance by using the given copper conductivity and crosssection area.2,8,29Therefore,except for the iron and PM losses in Ref.15,NN is also utilized here to cover the winding/copper loss correction in the motor optimization (will be discussed in Section 3).The following two subsections will discuss the analytical estimation models of iron loss and PM loss in detail.

2.2. Iron loss estimation

When a PMSM operates under the no-load condition, iron losses contribute the largest part of the motor loss because the current in winding is nearly zero and PM loss is much smaller. To calculate iron loss in the soft ferromagnetic material, modified Steinmetz equation is used with two different terms, hysteresis and eddy current loss. The specific iron loss parameter Wiron(W/kg) for a certain material is given as2,15:

where ^B is the peak amplitude of flux density and feis the motor electrical frequency,Ksfis the stacking factor of the lamination sheets (assumed 1 in this study). Khis the hysteresis coefficient and Keis the eddy coefficient. Kh,Ke,α1and β1are all Steinmetz coefficients which can be determined by fitting the loss data from manufactures for specific materials.In this paper, M235-35A steel is utilized for iron modeling whose Steinmetz coefficients can be found in Table 2.

The first assumption of using Eq. (6) is that the stator flux density must vary sinusoidally (with fe). However, in practice,the flux densities in stator tooth tip and in the back-iron parts linking stator base are far from sinusoidal. Furthermore, as discussed, analytical loss models traditionally use ^B of typical points to estimate the whole stator losses for the sake of simplicity. That also contributes to errors of analytical method compared with FEA models. Namely, the limit is that there is a non-uniform flux distribution on PMSM stator all the time. Lastly, flux saturation is not accounted for in this Stein-metz equation. To clearly demonstrate the flux variation and the limitations of Eq. (6), the following contents will choose two different iron models to discuss the comparison results of analytical method and FEA.

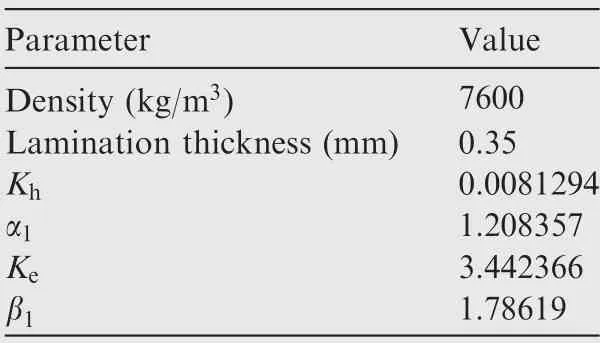
Table 2 Parameters of M135-35A steel for PMSM stator.

2.2.1. Plate

In order to get the ideal conditions of Eq.(6),this study modeled a plate in Infolytica MagNet (see Fig. 3(a)) with a simple current driven coil. An iron cube part (small die-square in the centre) is extracted for the iron-loss study. The side length of this cube is 3 mm and the depth is 54 mm. Fig. 3(b) depicts the flux variation of two cube points (Point A & B) in a time period. Obviously, in the lamination of cube, the flux density of every point is uniform,so it varies synchronously and sinusoidally with the coil current changes. In addition, there is no saturation in this cube due to the small input current in coil.Based on this plate model,Eq.(6)can then be compared with FEA.To calculate the loss in analytical model,we need to choose the flux density of one typical point.The ^B value from Point A(0.0638 T) is used to give the loss estimation which turns to be 8.33366×10-5W. The FEA in MagNet gives 8.33244×10-5W so the relative error of Eq.(6)is-0.015%.Therefore,the modified Steinmetz equation can estimate the iron loss as accurate as FEA based on the afore-mentioned assumptions.

2.2.2. Cube solid in motor stator

Based on the studied motor case in Ref. 15, a Pole-10-Slot-12 motor was modelled in MagNet.The studied cuboid locates at the centre of stator base, red part in Fig. 4(a). The red diesquare has a side length of 1 mm and the depth is 54 mm.Its centre location is (0, 45) mm in the motor cross-section.The variation of flux density of this central point is depicted in Fig. 4(b). The Root Mean Square Error (RMSE) with its corresponding sinusoidal curve is 0.05059 T.Though this sinusoidally tracking error is very small, the loss estimation of Eq.(6) performs much worse than the plate model above.

Motor FEA under transient with motion conditions(fe= 125 Hz) was performed in MagNet. The FEA iron loss of this cuboid is given as 0.0020272 W while analytical model using Eq.(6)predicts 0.001996 W(-1.52%difference).Therefore, even for this very small part in motor stator, the Steinmetz equation is prone to lose the estimation accuracy. The estimation error would be much larger if we only use the ^B of stator centre to give the whole stator power losses.

In order to mitigate the effects from the ^B changing between stator tooth and back-iron (yoke), this study divides stator into two parts: tooth and yoke, for loss estimation.More importantly, NN is utilized here to correct the estimation of Eq. (6) and establish its link with FEA results in a PMSM design space.

2.3. PM loss estimation

Three significant parts of motor losses are usually considered in the PM synchronous machines: iron losses, winding losses,and eddy current losses in PM.30However, in some optimization-oriented motor design models, power losses of PM are usually not accounted for because they are relatively much smaller than the iron loss.2,8,9Since in this study NN is expected to correct the loss estimation with very high accuracy, PM loss should be considered as a part of PMSM total losses.As shown in Fig.5,31the base PM loss model used here is assuming each PM as a plate of a sector of the circular ring.Eq. (7) from Ref. 31 is utilized to predict the PM losses:

Similar with the analytical methods in the above subsections, Eq. (7) only uses the BPMof one specific point in PM to calculate the whole PM losses, which can generate significant errors compared with the FEA. More importantly, for the method itself, it does not consider the PM eddy current reaction effect. The reaction effect makes the flux more difficult to pass through the PM and more flux line passes through the leakage path.14Therefore,it directly affects the generation and calculation of PM losses. Authors in Ref. 32 found that the reaction field should be taken into account when the machine is excited by a pulse-width modulated current, especially for high-speed machines. Ref. 14 found that, if the reaction effect is neglected, the analytical results can only match the FEA for the PM with large numbers of segmentations.In addition, as will be shown in the case study of Section 3.3,this analytical method is very sensitive to the PM height increase. Compared with FEA, the estimation error of Eq.(7) will quickly go up with regards to the PM height increase.

To solve the above-mentioned PM loss estimation problems, this study utilizes an adaptive factor kPMin NN to correct the loss estimation in a design space of PMSM without PM segmentation. As mentioned, this PM loss model can be replaced by any other desired models which will not affect the proposed NN-aided approach because the well-trained NN can smoothly and efficiently correct the PL estimation to the corresponding FEA results.

The next section will introduce the proposed NN approach in detail and a PMSM case will be given showing that,after the NN-based correction,the RMSE of PM loss estimation can be less than 0.004 W (around 0.23%-0.74% of the FEA values).

3. Average correction factor and NN aided approach

This section presents the NN aided correction approach for mass and loss estimation in PMSM design. Average Correction Factor (ACF) is utilized as a comparative method to demonstrate the excellent performance of NN in both mass and loss corrections. Their correction performance will be compared in a PMSM case. There are five correction factors,four for power loss correction and one for mass correction:PM factor(kPM),yoke factor(kYO),tooth factor(kTO),copper factor (kCO) and total mass factor (kMA). Both ACF and NN aided approach are giving these five factors based on the sample data from analytical models and FEA model but,as will be discussed, the methodology is totally different.

3.1. Average Correction Factor (ACF) method

ACF method was preliminarily investigated in Ref. 15; however,the estimation correction of PMSM mass and copper loss are not included in that paper.In contrast,this paper will compare ACF and the NN approach for both PMSM total mass and total loss correction.After NN training,the NNs will also serve the PMSM global multi-objective optimization, see Sections 4 and 5.

The ACF operation process is depicted in Fig.6 where Perf represents PL and M,MAT means the math/analytical model.First,we assume five correction factors all equal to 1 and there are n variables. Second, the first sample collection is exercised by only using up/down boundary values for each DV (this sampling scheme is named as ‘‘sweep2”), i.e. that we have 2ndesign points for joint simulation (math and FEA) to collect mass/loss results in this round. After that, the initial five cor-rection factors should be updated by a simple average operator using two groups (math and FEA) of 2nmass/loss data:

In the next step,replace initial correction factors(all 1)with the corresponding five knew,1in the math model and do the second round of collection (via joint simulation). In this round,sample 4 values for each DV (named as ‘‘sweep4”) which includes 2 boundary values, the other two are evenly distributed in the value range. Further, use the same average operator to calculate the second new factors:

whose only difference with Eq. (10) is operating on 4nmass/loss data instead of 2n. If all five knew,2are closed to 1 with small errors and,the relative errors of total loss and total mass of samples [Er, which is given by Eq. (12)] are all smaller than 3%for all 4ndata,the ACF validation is successful;otherwise,the validation fails.

3.2. NN aided approach

This paper employs a feedforward NN to implement the mapping from DVs to correction factors. Feedforward NN is a well-known supervised learning technique in the machine learning and artificial intelligence domain. NN is based on a non-parametric regression model. User does not need to specify the relations between the predictors (input) and responses(output) with a predetermined function since NN will learn them automatically by updating the internal training parameters (i.e. weights and bias).15,33

A basic feedforward NN comprises an input layer, one or more hidden layers and an output layer. Each hidden layer has one or several neurons, which can be set as a NN algorithm developer.25,33The data derivation principles from input to output layer via the hidden neurons can be found in the Section IV of Ref.22.It is noted that there are two different types of NN learning: regression15,22,25,33and pattern recognition25.The PMSM performance correction study here is not a classification problem thus this paper focuses on the regression learning. NN regression can be trained to a nonlinear model for specific tasks by using a very simple NN structure. Such a general nonlinear model can approximate any given inputoutput function with arbitrary precision.21,22Therefore, its excellent generalization capability is utilized here to correct the analytical PMSM sizing mass and losses in a large design space with very high accuracy.

As shown in Fig. 7, we use two NNs to correct power loss and mass separately,named as NN1and NN2.Both NNs have one input layer, one hidden layer and one output layer. For simplicity,weights and bias terms are omitted from the figures.The input elements of two NNs are both the studied DVs and they have the same hidden-layer structure (whose neurons are marked in green), but their output layers are different. The output elements of NN1are four correction factors for power losses: kPM,kYO,kTO,kCO, while there is one output element kMAin NN2for the PMSM total mass. Regarding the neuron number(q)in the hidden layer,as mentioned,it can be set as a NN algorithm developer but in the following studies,it is simply set as 6 by trial-and-error for both NNs. The reason is the fact that there are only 64 sample points (sweep4 scheme) in NN training thus we can get good regression performance with only 6 hidden neurons,which benefits from the excellent global generalization capability of NN.

In the training process, the raw data set was randomly divided into three data sets: training data (70%), validation data (15%) and test data (15%). Training data is used to directly modify weight and bias values;validation data is used for validating stopping condition and ranking of net candidates; testing data is used to obtain unbiased estimates of non-training data.25Therefore, only 70% of raw data are directly used for training NN, other 30% of raw data are new for the trained networks. It should be noted that the precision of NN turned out to be highly robust to data division ratios. Due to the small sample set and the great NN regression capability, empirical investigation has shown negligible differences in NN precision when the training set was from 50%to 90%.In the following contents,the RMSE of a trained NN is computed as the error between the whole raw data and the corresponding predicted data, which stands for the NN training/mapping performance.

3.3. Comparisons between ACF and NN approach

In order to demonstrate the excellent correction performance of the NN aided approach, a 12-slot-10-pole PMSM design case is illustrated to generate the mass/loss correction results using both ACF and NN. Three geometry DVs are studied here: axial length (l), stator tooth base fraction (αt) and PM height (dm), whose ranges can be found in Table 3. Different from Ref.15 which only focuses on the loss correction,PMSM input RMS current (I) is not considered as a variable here because the current has no relationship with the motor mass.Other PMSM parameters stay unchanged,as also summarized in Table 3.

The analytical PMSM sizing model in Ref.12 is used as the basis of this study which is a non-iterative and high dimensional sizing model. It can generate a comprehensive design of multi-physics fractional-slot PMSM in a very short time.This paper will use the afore-mentioned NNs to mainly link the estimated mass/losses of this sizing model to the FEA target values (from MotorCAD software) in a desired design space. Based on that, a multi-objective PMSM global optimization can be quickly finished(as it will be discussed in Sections 4 and 5).

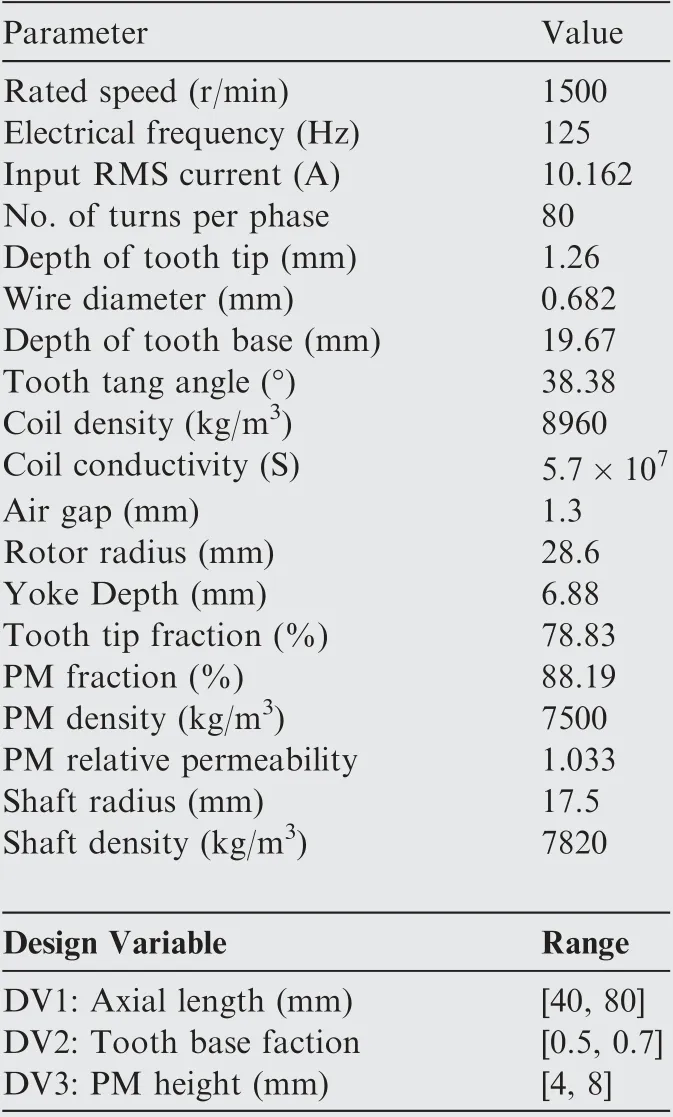
Table 3 Parameters and variables of PMSM case for correction performance comparison.

In this section,DV1,DV2 and DV3 are l,αtand dm,respectively. Both ACF and NN approach are tried to correct the estimated PMSM total losses and mass. In order to use ACF, as discussed in Section 3.1, we need to do two rounds of joint simulations between which the five correction factors should be updated. The updated correction factors in Eq.(10) (knew,1), as well as the knew,2in Eq. (11) after the second round of joint simulation,are all given in Table 4.On the other hand, to implement the NN approach, the 64 samples from sweep4 are processed as the input-output training data set following the designs in Fig. 7. Then, two NNs can be trained using the train command,which is a part of MATLAB’s Deep Learning Toolbox,in 1 s on a standard computer.After training,the absolute RMSE results(using 64 raw data)for the predictions of five correction factors are given in Table 4.

It is hard to depict the variations of two objectives against three variables. Therefore, before showing the correction relative errors of ACF and NN, the series numbers of design points for 3-DV combinations are defined. Fig. 8 shows the overall scheme of sweep4 and sweep5. As discussed in Section 3.1,the first and the last values of each DV are the boundary values of their ranges while the other sampled values are evenly distributed in the middle. For example, in sweep5, a1and a5are the lower and upper boundaries of DV1, and the distance of adjacent values equals (a5-a1)/4. On the other hand, Fig. 8 also depicts the series number of DV combinations for each sample value of DV3. Obviously, in sweep4,when a value of DV3 is confirmed, there will be 4 × 4 designs whose series numbers are marked as 1,2...,16.And in sweep5,the series numbers are given as 1,2...,25 for each value of DV3.approach provides a much better correction performance. In all sub-figures of Fig. 9, the NN approach can predict at least one order of magnitude closer to the FEA target value. Especially for mass correction, the relative errors of ACF method can be thousands of times bigger than the NN approach.

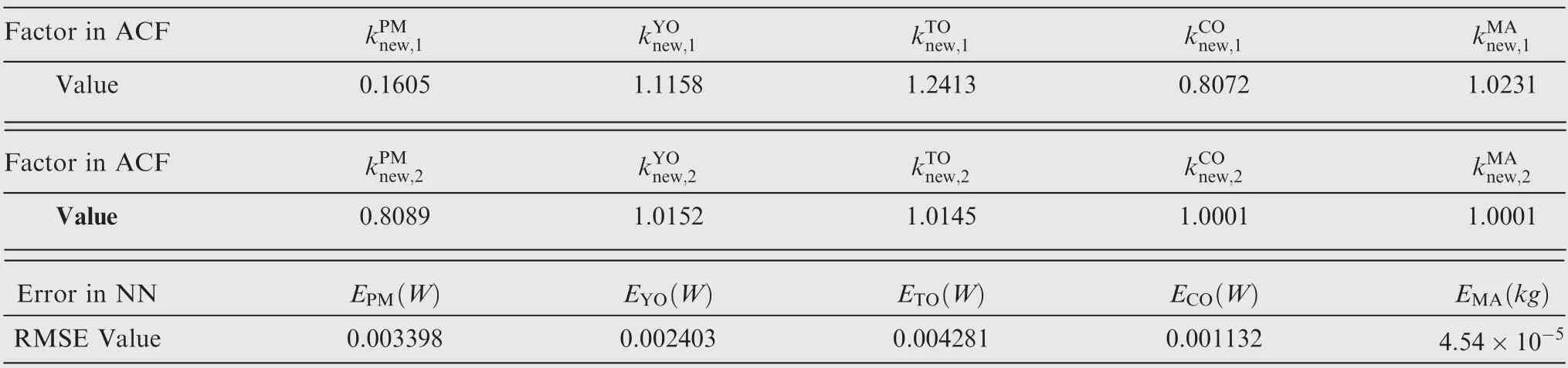
Table 4 Correction factors in ACF and RMSE results in NN approach.

It is important to note that,in sweep5,third fifths of sample points are not included in sweep4 sampling which provides the raw training data (64 samples) for two NNs. But, as shown in Figs.9(b)and(d),NN approach can still correct the analytical loss/mass with very high accuracy even the sample was not used for NN training. Therefore, instead of the timeconsuming FEA model, the NN approach can be further applied into the global analytical PMSM optimization, which will be illustrated in the next two sections.

4. NN aided multi-objective optimization procedure

This section presents the proposed NN aided multi-objective optimization methodology. As shown in Fig. 10, it is a threestage-seven-step procedure. Three stages in this methodology are: PMSM modeling, NN training and multi-objective optimization. In the first two, there are three steps in each stage while the last step is in the third stage. Three stages will be introduced separately, as follows.

At the beginning of modeling stage,we should first confirm the PMSM pole-slot topology, input parameters, design variables(and their ranges)and output performance indices(mass and power losses in this study). Then, establish the analytical model which can derive the output performance by using the given lumped parameters and math functions. After that, the joint simulation between the analytical model and the target FEA model should be built for sample data collection. This study is using MATLAB for the analytical modelling and collect FEA results from MotorCAD. Other software platforms should also be feasible and compatible with the methodology as long as they can generate satisfied results of performance indices with regards to the studied DVs. The next stage would be training NNs to bridge the gap between the analytical and FEA models.

The ranges of DVs form the design space of the studied optimization problem. In the first step of NN training stage,samples are collected by the joint simulation built in the previous stage. This study suggests using the sweep4 sampling scheme which evenly samples four values for each DV(see Section 3.3). After that, the raw data of samples should be processed as the input-output training data set following the designs in Fig. 7. Namely, the input elements are the DVs for two NNs; however, the output elements are four loss correction factors for NN1while only the total mass correction factor is in the output layer of NN2. After the training data preparation, the last step of NN training stage is to train two feedforward NNs. Many commercial NN training tools can be utilized, e.g. Deep Learning Toolbox in MATLAB.

After the modeling stage and the NN training stage are accomplished, two desired NNs are prepared and can become fast surrogate correction models for the performance indices which are objectives of the studied PMSM optimization problem. Thus, in the final step of the methodology, we can leave the time intensive FEA model and do the optimization in the original design space by only using the analytical models and the trained NNs.Noting that the optimization in any subspace can be exercised in the same way. Since both analytical model and NNs are mathematic thus very efficient, exhaustive algorithm is used in this step for the global optimization, i.e. that sample large number of design points in the whole design space and generate all corresponding values of objectives.

Lastly, in order to generate the best design point, an integrated index r of two objectives is utilized to select one particular point for the Pareto front in the objective space, the criterion for this decision-making solution is the minimal distance from ideal objectives24,25,34:

where Miis the mass of the ithsolution; Mmaxis the maximal mass of all designs; PLiis power losses of the ithsolution;PLmaxis the maximal power losses of all designs; λMAis the weight of mass objective.

λMAis usually set as 1 which means two objectives have the same priority. But, in practice, different objectives can be prioritized by changing the weight value in Eq. (14). Obviously,the best design obtained from Eqs. (13) and (14) will differ with regards to λMA.In particular, when λMAincreases, power loss of the best design will climb up while the mass will decrease. For the MEA application, λMAis usually set larger than 1 since the mass objective has a higher priority.

It is noted that,the proposed NN aided approach should be independent with the PMSM’s operational scenarios. The scenarios’parameters can be fixed in the optimization or,they can be set as the design variables as well. No matter for which situation, the general procedure of the proposed NN aided PMSM optimization methodology would be the same (as shown in Fig.10).For the case study in Section 5,the PMSM is used for an actuator onboard MEA. The design space of PMSM optimization would be different for different PMSM application scenarios, either actuation or generation. Moreover, the design space should be predefined before the NN aided optimization process.

5. PMSM case for multi-objective optimization

5.1. DV selection

Based on the PMSM case in Section 3.3, three DVs are newly selected for the PMSM optimization case. In order to demonstrate the trade-off study between two objectives, we initially investigated the sensitivity of two objectives with regards to different design parameters and then, chose the ones whose variations of two objectives are converse. For example, when αtbecomes larger, the motor mass would increase while the total losses would decline. Besides, the airgap height and wire diameter have the same variation situation with αt.In contrast,we found that the two objectives would show the same varia-tion trend against the changes of axial length, PM height and tooth base height.

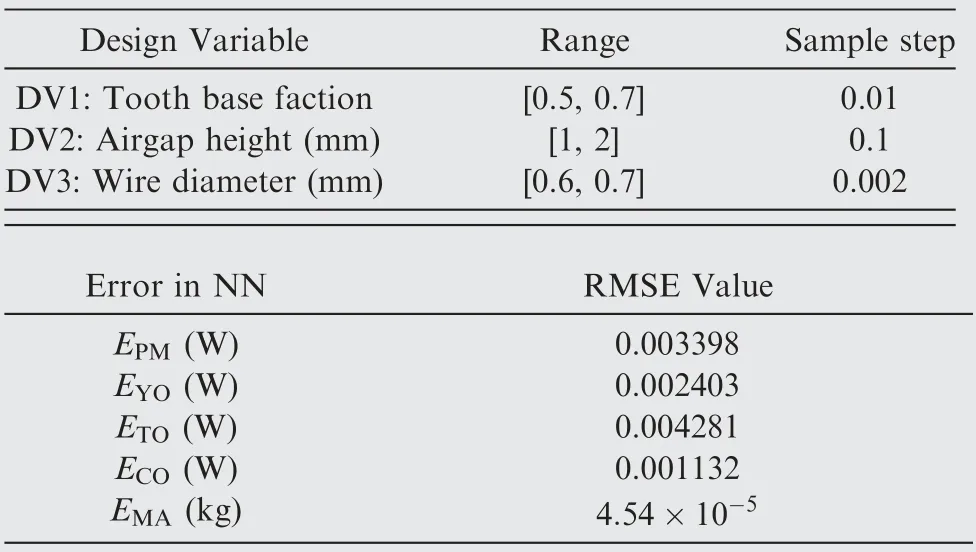
Table 5 Variables,sample step and NN training performance in PMSM case for optimization.

Therefore, the three DVs in this section are: stator tooth base fraction (αt), airgap height (hag) and wire diameter(Dwire) whose ranges are given in Table 5. Axial length and PM height are unchanged in this section whose values are 54 and 4.4 mm. Other parameters are the same with Section 3.3.It is noted that the DV selection will not affect the optimization procedure discussed above. Namely, the optimization methodology would be the same for all DV combinations.

5.2. NN training and optimization results

In the NN training stage of optimization,sweep4 sampling was again used for the training data preparation. Therefore, 64 samples were collected from the joint simulations and processed as the input-output data set for two NNs. Then, two NNs were trained using the train command in MATLAB’s Deep Learning Toolbox, both in 1 s.The RMSE training performance of two NNs are given in Table 5 which are in the same level with the NNs in Section 3.3. Finally, as shown in the bottom of Fig. 10, sample large number of design points in the 3D design space of αt,hagand Dwire,the objective values of all these designs can be quickly obtained by using the analytical model and two trained NNs.

In this case,the small steps of DVs for the global optimization are given in Table 5 thus, we sampled 21 values of αt, 11 values of hag, and 51 values of Dwire.The total sample number is 11781 and the collapsed time for generating all the objective values of samples is 365.44 s on a standard computer. Then,the optimal design was then simply obtained by finding the lowest value of r in Eqs. (13) and (14), which can be done in MATLAB almost instantaneously using the embedded min function. The PMSM optimization results are depicted in Fig. 11.

All the design points in optimization as well as six Paretofront points are presented.The objective value distributions of design points are shown in Fig.11(a)where there is a clear Pareto front at the bottom-left side. Two objectives of all designs were integrated into one (r value) by using Eqs. (13) and (14)with a specific λMA. This study swept λMAvalue from 1 to 6 and used Eqs. (13) and (14) to generate the six Pareto-front points in Fig. 11(a) (Mmaxand PLmaxshould be found beforehand). Obviously, with the increase of λMA, power loss of the best design goes up while the mass declines. Since this study is for MEA applications, mass should have a priority over the other objective thus, λMAis set as 3 here for the final best design confirmation.In the same subfigure,the 64 samples collected from joint simulations are also shown, which demonstrates that the sample amount is very small compared with the optimization sampling.

On the other hand,Fig.11(b)shows the design points in the 3-Dimensional DV space (αt,hagand Dwire). Noting that the color of design points only shows the r value distribution when λMA=3.The color distribution will be changed with different λMAvalues.In this subfigure,there is a clear trend that the distance from the ‘‘Best Design” in this 3D space has a positive relation with r value, i.e. the far the larger. Corresponding to Fig. 11(a), the three DV values of six Pareto-front points are marked in Fig. 11(b) among which the minimum-r design of‘‘λMA= 3” is the final best design point in this PMSM optimization case.

Finally,after finding these six Pareto-front points,their 3D values were input into the FEA platform, MotorCAD, to verify the accuracy of the NN aided optimization methodology.As summarized in Table 6, all performance results are extremely close to the target FEA values no matter for mass or power losses. The relative errors (absolute value) of M are all below 0.01% and for PL, the relative errors are around-0.15%. Therefore, the mass mapping performance (NN2) is better than that of power losses (NN1). This conclusion can also be reflected by the NN RMSE results in Tables 4 and 5.It should be noted that most of the six Pareto-front points are not included in the 64 samples, which again validates the excellent performance of NN aided optimization approach.

5.3. Comparison with FEA-based optimization

Compared with the conventional FEA-based optimization,the first advantage of the proposed methodology comes from the efficiency of doing optimization. As discussed, the sample amount of NN training (obtained from joint simulation) is very small, which means we can work on the timeconsuming FEA model in a very short time and then do the optimization by only using the trained NNs and analytical models.In this study,the proposed NN approach can generate a PMSM design in 0.04 s while it costs more than 1 min in the FEA model.

Another advantage of the NN approach is that it has no risk of getting stuck in local optimum, it is a global optimization approach using the exhaustive algorithm. Since the FEA consumes much time, it is usually not realistic to use the exhausted method to generate the multi-objective optimization.23Popular solutions are using search algorithms, e.g.genetic algorithm.23-25,34,35However,in that case,we still need to sample hundreds even thousands of design points to get the Pareto front for a multi-objective optimization problem.More importantly, search algorithms would bring the risk of getting stuck in local optimum.

Table 6 Performance verification of six Pareto-front points.

Last but not the least,the hybrid model of trained NNs and math models can provide the best design point smoothly for any potential DV subspaces, also in a very short time. However, for the FEA-based optimization with search algorithms,we may have to run the FEA model once and once again for the new optimization problems because,in a subspace,the previous searched samples can be very little thus cannot be utilized to give the optimal design.

However,there is one limitation of the proposed NN aided optimization approach: the trained NN may not work well for the variable ranges out of the original design space.Namely,if enlarge the design space, the prediction performance of the trained NN may be affected.The reason is that the raw data collected for NN training do not cover the entire design space.For the design points out of range,the FEA model is still needed for the accurate performance estimation though it is not efficient.Therefore, for the method generalization, it is suggested the motor variables and their design ranges should be well selected before the data collection and the final NN training.

6. Conclusions

In this study a hybrid model of NN and analytical model is proposed for the fast and accurate multi-objective global PMSM optimization. Based on some samples collected from the FEA model, two NNs are trained for the mass and loss correction separately to serve the optimization in the PMSM design space. Two PMSM design cases are described in this paper. The first case demonstrates the excellent NN training performance under the comparisons with the ACF method;the other case validates the proposed NN aided optimization method with the globally optimal results and compares it with the conventional FEA-based optimization.

In general,the NN aided approach for PMSM optimization mainly accounts for the data of inputs (design variables) and outputs (performance correction factors); therefore, the application should not be limited to the typical types and topologies of electrical machines.In addition,apart from mass and power loss,other machine performance indices can also be considered in the multi-objective optimization using a similar way.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This project has received funding from the Clean Sky 2 Joint Undertaking under the European Union’s Horizon 2020 Research and Innovation Programme(No 807081).Mr.Yuan Gao would like to thank Dr. Benjamin Cheong (Nanyang Technological University)for valuable and helpful discussions that preceded the preparation of this paper.