Failure behavior analysis of phased-mission systems considering functional and physical isolation effects
Ying CHEN, Ze WANG, Rui KANG
School of Reliablility and Systems Engineering, Beihang University, Beijing 100083, China
KEYWORDS Failure mechanism;Phase-dependent damage accumulation;Phase-dependent degradation;Physical isolation effect;Reliability evaluation
Abstract Phased-Mission Systems(PMS)are widely applied in aerospace,telecommunication and intelligent systems for multiple, consecutive and non-overlapping phases of missions. The phasedependent stresses and system structure cause some difficulties to the reliability analysis of PMSs.In this paper, we analyze the physical isolation effects on the degradation speeds and across-phase damage accumulations of failure mechanisms.And,some corresponding reliability and unreliability formulas are derived. Besides, a hierarchical Binary Decision Diagram (BDD)-based modeling method is proposed for incorporating functional and physical isolation effects into BDD models,and the analytical method with phase algebras is introduced for studying the failure behavior of PMS with functional dependence. In the case study, we evaluate the collision avoidance system of a fixed-wing unmanned aerial vehicle as an example to demonstrate the proposed modeling and analysis method. Results show that the physical isolation effects have significant influences on the degradations of components,which deserves detailed analysis for a more practical and realistic PMS’s failure behavior.
1. Introduction
Phased Mission Systems (PMSs) are designed to accomplish multiple, consecutive and non-overlapping phases of missions[1,2]. They are widely applied in aircrafts, telecommunication systems, intelligent vehicles, etc. Phase-dependent system structure and stress conditions distinguish the PMS from other complex systems [3-6].
In different phases of a mission, the system structure and the success criteria of a PMS may be variable [7]. The basic problem that reliability analysis methods need to address is the dependent statuses of a component in sequential phases.Somani et al. [8] developed a Markov-based reconfiguration method to analyze the reliability of PMS with either deterministic or random durations of phases. By applying Continuous Time Markov Chain (CTMC) model, Kim et al. [9] analyzed the time-dependent reliability of nonrepairable PMS with heterogeneous components having phase-type time-to-failure distributions. However, the fundamental assumption of the Markov-based models is that the lifetime of each component follows exponential distribution, which limits its practical application. In addition, the well-known state explosion problem of Markov-based methods is also disturbing [10].
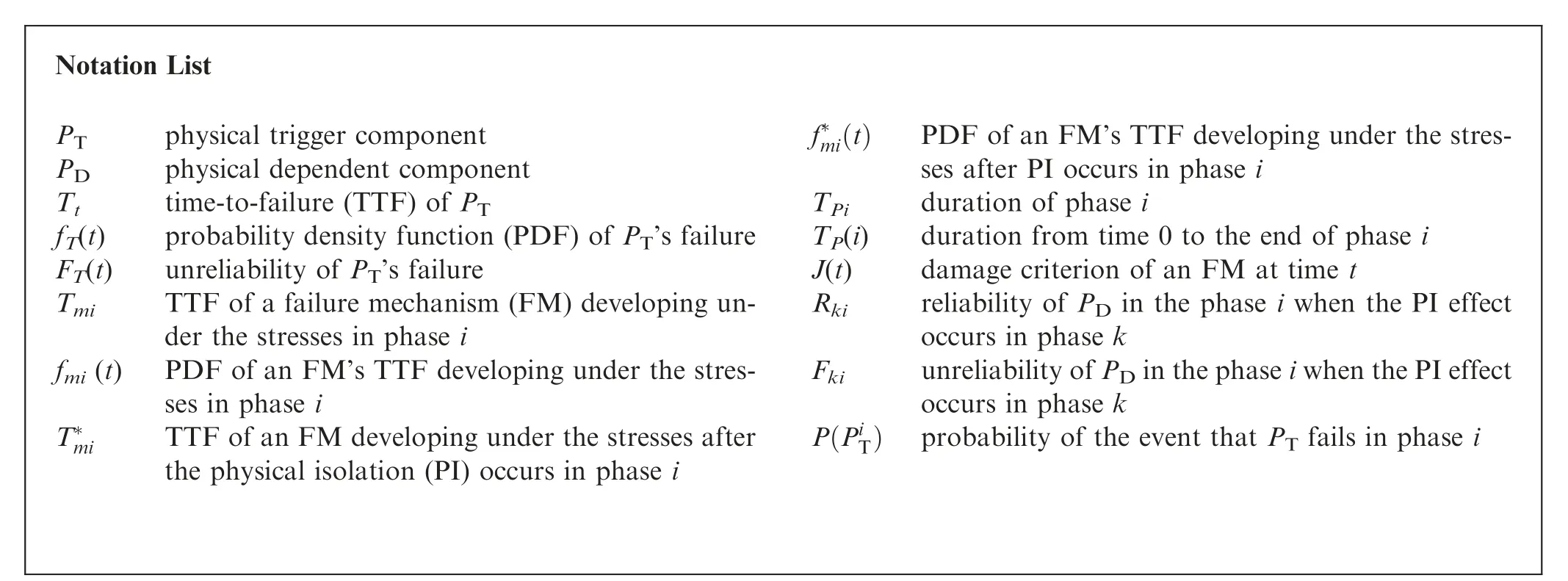
Notation List PT physical trigger component PD physical dependent component Tt time-to-failure (TTF) of PT fT(t) probability density function (PDF) of PT’s failure FT(t) unreliability of PT’s failure Tmi TTF of a failure mechanism (FM) developing under the stresses in phase i fmi (t) PDF of an FM’s TTF developing under the stresses in phase i T*mi TTF of an FM developing under the stresses after the physical isolation (PI) occurs in phase i f*m i(t) PDF of an FM’s TTF developing under the stresses after PI occurs in phase i TPi duration of phase i TP(i) duration from time 0 to the end of phase i J(t) damage criterion of an FM at time t Rki reliability of PD in the phase i when the PI effect occurs in phase k Fki unreliability of PD in the phase i when the PI effect occurs in phase k P(PiT) probability of the event that PT fails in phase i
To analyze the reliability of a system with components having non-exponentially distributed Time-To-Failures (TTF),some explicit and analytical methods were devised. Wang et al.[11]provided the formulas to compute the state probabilities of the system in different phases.An explicit expression of mission reliability was also delivered for the PMS with the same component requirements in all phases. In addition to internal failure, such as degradation of components, Peng et al. [12] also took into account the external impacts, such as meteorite and radiation, when they analyzed redundant PMS with or without overarching protection. Although these explicit methods or algorithms have no limitation on the type of lifetime distributions,they are hard to implement during the reliability assessment for large-scale and complex systems.
As an effective tool for handling the complex Boolean operation and Shannon decomposition, Binary Decision Diagram (BDD) models are widely used in the reliability analysis of phased-mission systems [13-16]. In 1999, Zang et al. [17] firstly used phase algebras to deal with the statusdependence across phases. Two BDD operations, Forward and Backward Phase-Dependent Operations (FPDO and BPDOs), were proposed to operate the phase algebras during constructing BDD models for PMSs, which have been widely applied. To improve the two operations, Xing and Dugan[18] proposed a recursive removal process to eliminate the unreasonable nodes of the PMS’s BDD model generated by the PDOs.
Functional Dependence (FDEP) is very common in many complex PMSs with dynamic dependence. Functional dependence refers to that functions of some components (called dependent components)rely on the operation of other component(called trigger component)[19].Considering the propagation phenomenon of some components’ failures, such as computer virus [1], Xing et al. [20,21] introduced an isolation effect that the failure of a trigger component causes dependent components to become unusable,inaccessible or isolated.They thought that when the trigger component fails prior to the dependent component,the propagated failure of the dependent component cannot affect other components [22]. But in practice, the impact of environmental stresses, such as heat, vibration and Electromagnetic Interference (EMI), caused by dependent components can’t be isolated easily by the failure of a trigger component.So, the isolation that Xing et al.studied should be regarded as functional isolation, while the isolation effect on environmental stresses was ignored in their work.
In Ref. [23], Chen et al. proposed a Physical Isolation (PI)effect studying components’effects on the environmental stresses. After a component (called physical trigger component,named PT) fails, some components (called physical dependent components,named PD)are no longer affected by the environmental stresses induced by PTduring its function. So, we call PDisolated from the physical influence of PT, and this phenomenon is defined as PI effect.
Except for the phase-dependent statuses of a component,the stress conditions may change from phase to phase,leading to different degradation speeds of components. Some papers[24 25]adapted different failure rates or distributions for components in each phase during their analysis about PMSs.Mostly, the s-independence of a component’s lifetimes among phases was assumed, which may lead errors to the analysis comparing to the real practice. So, in Refs. [26-29], the phase-dependent stresses on the failure of the component were accounted by using the concept of equivalent age associated with Cumulative Exposure Model (CEM). But without a detailed study on the degradation process, it’s quite difficult and time-consuming to determine acceleration factors for different components in different stresses.
Failure Mechanism (FM) is a process that a component or structure fail due to the root cause of physical or chemical stresses [30]. By using Probabilistic Physics-of-Failure (PPoF)models containing material properties and stresses that component suffers, the probabilistic distribution of an FM’s TTF can be obtained through Monte-Carlo simulation [31].According to how the FMs are affected by different stresses,Chen et al.[32]categorized FMs into three types:Environmental load-triggered (E-type) FMs, Operating load-triggered (Otype) FMs, and Combined load-triggered (C-type) FMs. It’s noticeable that environmental load is the same as environmental stress, while operating load (or operational stress) means the power making the components functional, for example electricity for electronic devices and force for mechanical parts.Besides, Chen et al. [33] proposed four kinds of FM dependences, i.e., competition, trigger, accumulation, and acceleration/ inhabitation, for illustrating the failure behavior of complex systems.
The main contributions of this paper are as follows: firstly,the failure behavior of a component in PMS considering PI effect is discussed, and the explicit reliability formula of the FM affected by PI effect is derived, which can help reliability engineers to study the detailed degradation processes.Besides,a hierarchical BDD-based modeling method incorporating PI and functional isolation effects and related analysis method are proposed to simplify the analyzing difficulty and demonstrate the failure behavior of a PMS with FDEP groups.With the proposed method, more accurate and realistic reliability results of PMSs can be obtained, while most existed methods ignored the PI effect on the across-phase damage accumulation.
The remainder of the paper is organized as follows: Section 2 describes the accumulative degradation of FMs sensitive to the PI effect,and derives the reliability and unreliability formulas of a component under the independent influence of one FM.In Section 3,the modeling and analyzing methods considering the physical and functional isolation effects are introduced and illustrated with an example PMS with an FDEP group.As for the case study in Section 4,we evaluate the failure behavior of the collision avoidance system of a fixed-wing Unmanned Aerial Vehicle (UAV) with consideration of PI effect. Section 5 gives conclusions as well as the future work.
2. Failure behavior of a physical dependent component
2.1. Physical isolation effect and assumptions
In practical engineering, the failure of dependent component can not only affect the failure of other parts within the FDEP group through the trigger component, but also affect the degradation of its nearby components by changing the environmental stresses,such as thermal stress,humidity or electromagnetic field.
It is worth noting that the PI effect studied in this paper must have definite physical trigger and dependent components.Besides, even if a component is physically isolated from other component’s physical effect,it will still be affected by the basic environmental stresses of mission profiles.
For example, in electronic products, when the power transistor works, it generates a lot of heat and causes the ambient temperature to rise. After the power transistor fails, the ambient temperature decreases considerably. At that time, the development speeds of the FMs, affected by temperature, in the components adjacent to the power transistor will change accordingly.
In the phased-mission system, a component may be exposed to many levels or magnitudes of phase-dependent stresses because of its special mission profile. Moreover, the physical isolation effect will incorporate more changes and uncertainty into the stress conditions. In Fig. 1, we demonstrate a typical PMS’s environmental and operational stress conditions considering PI effect.
From Fig.1,we can see that after PI occurs,some environmental stresses may change to different levels, while the increase or decrease of these stresses may vary from phase to phase because of the design and profile of PMS.But the operational stresses are not affected by the physical trigger component at all. Next, we will discuss how three kinds of failure mechanisms may be affected by the PI effect.(1) O-type FMs
These FMs are only sensitive to the operational stresses when their relative components are working,which means that they won’t be influenced by the PI effect that causes the environmental stress changing.Such as the electrical breakdown in integrated circuits, it will develop under the high density of electric current, but some environmental stress changes induced by its nearby components cannot influence its degradation. So, these FMs can only suffer some limited changes which is the same as the number of the mission’s phases.Chen et al. [32] had derived the unreliability function of a component under the independent influence of an FM that is exposed to n changes of stresses.So,the unreliability formula of a component under the independent influence of an O-type FM in phase k is:
where, the first part means the probability of the component failing at phase I, and the second part means the component failing at phase j (1 <j ≤k-1).
(2) E-type FMs
E-type FMs refer to the FMs which will develop at a certain speed as long as the trigger environmental stress exists. After physical isolation occurs and environmental stresses change,some of the E-type FMs, not all E-type FMs, will develop at different speeds. For example, the changes of thermal stress caused by the PI effect affect the degradation of thermal fatigue,while the vibration fatigue won’t act in the same way even though both of them are E-type FMs. So, we should identify the FMs which will be influenced by the environmental stress changes due to the PI effect. If one E-type FM is not sensitive to the PI effect, then its unreliability formula can be obtained as Eq. (1). In Section 2.2, we will derive the explicit reliability formulas of a physical dependent component under the independent influence of E-type FMs.
(3) C-type FMs
The activation of a C-type FM depends on the combined effects of the environmental and operational stresses. Just as we mentioned above,the operational stresses won’t be affected by the PI effect,so when analyzing the exact degradation processes of O-type FMs, the environmental stresses should be paid more attentions. As for the reliability formulas, the Otype and E-type FMs will share the same forms.
In practice, all components of a PMS will have their own physical effects on the stress conditions, and are subject to the complex and coupling stresses. In order to study the PI effect on phased-mission system’s reliability, this paper is based on the following assumptions:
(A) The components in the system are irreparable and binary states. No component or product can be recovered from failure or unavailability, and there are only two states, i.e., function and failure.
(B) The propagated failures of components are ignored.
(C) The sequence and durations of the phases of a mission are predetermined.
(D) The impact of physical trigger components on the surrounding environment will change only when they fail.In addition, compared to the long lifetimes of components, the durations of these changes are negligible, so those changes are considered to occur instantaneously.(E) To simplify the difficulty of the study,a component cannot be a physical trigger component and a physical dependent component at the same time. And the physical dependent components can be influenced by only one physical trigger component.
(F) The across-phase damages of an FM caused to the component are accumulated linearly.For studying the damage accumulation process, after the TTF’s distributions of an FM under some certain stress conditions are obtained by PPoF [31], the development speed of an FM is assumed to be a constant value that is inversely proportional to its TTF.
2.2. Reliability of PD affected only by an FM
Next, we will mainly analyze the physical isolation effect on the degradation of an affected FM in a PDperforming a nphase mission. It is assumed that the stress conditions of all phases are different, which may lead to n different development speeds of an FM in different phases. Considering the PI effect on environmental stresses, the corresponding FM development speeds are more complex, as shown in Fig. 2.
The durations of n phases are tP1, tP2, ..., and tPn, respectively. Before the failure of the physical trigger component(PT), with assumption (6) and different stresses of n phases,the ideal TTF of the FM that develops only at the stress condition of phase i is assumed as Tmi(i = 1, 2, ..., n). Let the damage threshold of the FM be‘1’,so the development speeds of FM in different phases, vm1,vm2, ..., and vmn, will be 1/Tm1,1/Tm2,..., and 1/Tmn.
In Eq. (3), the first part means the accumulative damage before phase i, and the second part demonstrates the damage newly caused to the component in phase i.
Only when the damage criterion is smaller than its threshold, previously assumed as ‘‘1′′, can a component under the independent influence of the FM be reliable. Therefore, the reliability of PDindependently affected by the FM in phase i is:
It’s obvious that if PTis perfect, i.e., Tt= inf, Eq. (4) can demonstrate the reliability of O-type FMs, like Eq. (1).
(2) Reliability of PDin phase k affected only by the FM
After PTfails in phase k,the surrounding stress of the physical dependent component in this phase may change, and so does the development speed of the FM.So,at time t,the damage criterion of the FM in phase k is as follows:
(3) Reliability of PDafter phase k affected only by the FM
After the PI occurs in phase k, the stress conditions that physical dependent component suffers are different from those before PI.So,in phase i(k <i ≤n),i.e.,TP(i-1)<t ≤TP(i),the damage criterion of the FM can be expressed as follows:
2.3. Probability of PD in different phases affected only by the FM
In the Section 2.2, if the phase at which the physical trigger component fails is known, the conditional reliability of the FM in each phase is introduced.Then,the conditional reliabilities of PDindependently affected by an FM can be integrated into a n × n matrix, as follows:
3. Failure behavior modeling and analysis
In practical engineering, in order to achieve multi-phase mission, the configurations of the PMS in different phases are often different. In this section, we will discuss the modeling and analysis methods for the failure behavior of PMS with FDEP groups. The process of failure behavior modeling method considering physical and functional isolation effect is shown in Fig. 4.
3.1. BDD models of system structure
Phased-mission system can be seen as a combination of several single-phase systems. At first, the system structure, i.e., the logic relation among components’ failures in every phase,should be analyzed, and the Fault Tree (FT) model can be generated.
Besides, according to the function designs of PMS and detailed analysis of environmental effects caused by operational components, we can identify both the FDEP and PI effects among components.Moreover, the impacts of all components’failures on the stress conditions should be quantified.Combining the experts’experience and the difficulty of analyzing these impacts,select some most concerned,serious,or critical PI effects for further study.
In this section, we provide a three-phase mission-system as an example for illustrating the modeling method, and its FT models in 3 phases are shown in Fig.5.It’s assumed that either failure of three phases leads to the failure of the mission.
In Fig.5,component A and B are needed in phase I and III,while component B and C are essential in phase II. After the detailed analysis of the example system, the function of component B needs the assistance of component T, and the PI effect of component B on A cannot be ignored.When not considering the propagated failure of functional dependent component B, the logic OR gate can take place of the FDEP gate in Fig. 5 [21,34,35].
For a traditional BDD model, each non-sink node has 2 out-going edges, 0-edge and 1-edge, representing the reliable and failed statuses of an element, respectively. According to the BDD modeling method for the single-phase systems [36],the components linked to logic OR gate in the FT model can be connected with their 0-edges, while the components linked to logic AND gate should be connected with their 1-edges.For example, the FT model in Fig. 5 (a) can be transformed into a BDD model shown in Fig. 6 (a), where, the marks on the upper right of non-sink nodes are used for showing the exact phase when the component is required.
After obtaining all the BDD models of the system structure in 3 phases, many researchers chose to use the FPDO or BPDO algorithm [17,37] for cancellation of common components, which means phase algebra will be done during the BDD modeling process. But this algorithm requires sophisticated skill to perform the phase algebra while modeling, and with FMs being considered, the PDOs will be relatively difficult to the failure behavior modeling, especially for the PMSs.
So, in this paper, according to the logic OR correlations between different phases, we connect the BDD models of system structure in different phases together by connecting their 0-edges. Therefore, the BDD model of the example system structure is combined as Fig. 6 (b). By the way, in this paper,we choose to operate the phase algebras after construction of the entire system BDD model.
During analyzing the BDD model, the reliability (or unreliability) can be calculated by travelling the paths from root node to sink node ‘0’ (or ‘1’) [13]. Take the BDD model of phase I in Fig. 6 (a) as an example. From Fig. 6 (a), there are two paths from root node to sink node ‘1’: (1)A1→T1→1, and (2) A1→T1-→B1→1. So, the unreliability of this BDD model is the sum of probabilities of two paths:
where, R(x) and F(x) represent the reliability and unreliability of component x (x = A1, T1, B1), respectively.
3.2. BDD models of components
According to partial results of Failure Mode,Mechanism,and Effect Analysis (FMMEA), the main FMs of components,FMs’types and correlations can be obtained.In this paper,we only consider three correlations among FMs [33]: competition(MACO),damage accumulation(MADA)or parameter union(MAPA),and acceleration(MACC)or inhibition(MINH).
After analysis of the PI effects chosen in Section 3.1,we can determine which one of the E- or O- type FMs in physical dependent components may be affected.
Assume that component T has two FMs,MT1and MT2,and their correlation is MACO,which means that when the damage caused by either of them reach its corresponding damage threshold,T is failed.According to[33],the Failure Mechanism Tree(FMT) model of component T is Fig. 7 (a), and same to logic OR[32],their competing failures can be modeled in Fig.7(b).
Component C has two FMs, MC1and MC2, and their correlation is damage accumulation (or parameter union), which indicates that these FMs cause damages to the same position of the component (or contribute to the shift or degradation of one parameter).According to[33],the FMT model of component C is Fig. 8 (a). Considering the cumulative effects of these two FMs,the nodes in a BDD model are connected with their 1-edge, similar to logic AND [21]. But for distinguishing the MADA from logic AND, some modifications are made and shown in Fig. 8 (b).
The acceleration (or inhibition) correlation refers to a phenomenon that after the occurrence of an event or a component’s failure, some FMs will develop at different speeds from their former rates[21].The proposed PI effect is one special case of MACC/MINH, so, component A and B will be used to illustrate MACC/MINH. Suppose that component A has one FM, MA, and MAis an E- or C- type FM that is sensitive to B’s PI effect. So, the FMT model of component A is Fig.9(a)[21].In Fig.9(a),MAmeans this FM develops under the stress conditions before PI effect occurs, while M*Arepresents this FM develops under the changed stress conditions after PI effect. Considering the possibility of that MAmay develop to fail at two different speeds, the BDD model of A is shown in Fig. 9 (b) [32].
Assume that there is only one FM, MB, in component B should be analyzed. So, with the modeling method mentioned above, the FMT models of all components can be generated,and will be transformed into BDD models for further analysis.
3.3. Combination of BDD models and analysis
The nodes in system structure BDD model representing components in different phases should be replaced by their corresponding component BDD models, and the symbols indicating the phase at which the FMs are should be added to their nodes’ upper right corners. Thus, the system final BDD model can be obtained, like Fig. 10.
After obtaining the final BDD model,all the paths to sinknode‘1′(or‘0′)should be traveled for the unreliability(or reliability)of the system.Just as we mentioned in Section 3.1,the proposed analytical method operates the phase algebra after BDD model’s construction. So, when we analyze the paths,we should use the phase algebras (shown in Table. 1 [17,37])to reduce the invalid paths and identify the failure or functional status of FMs in every phase.
Besides,there is another phase algebra(d)needed to handle the path analysis, which is:

Table 1 [17,37] Rules and Physical Meanings of phase algebras.
4. Case study
4.1. Description
In this section,we use the collision avoidance system of a fixedwing UAV as an example to illustrate the modeling and analyzing methods. It is known that this UAV is required to perform a three-phases mission in sequence: working in the plain area(phase I),forest area(phase II),and hilly area(phase III),with durations of 2500 h, 1500 h and 6000 h, respectively. If any one of the phases is failed, the whole mission will be regarded as a failure.
It is assumed that the operational stress conditions of the UAV remain unchanged in each phase, but the environmental load has obvious changes: the vibration in the forest area is much greater than it in the hilly area, while it in hilly area is greater than in plain area; temperature cycle in forest area is more serious than in hilly and plain area.
The dynamic fault tree model of collision avoidance system is obtained in Fig.11,and meanings of the symbols are shown in Table 2. According to the functional analysis of the whole system, we find that the long-range transmitting antenna only works when the UAV flies faster than a certain speed.Assume that the long-distance transmitting antenna does not work in forest areas,but is acquired to be operational in plain and hilly areas. For demonstrating the mechanical parts, the brakes of undercarriage are also considered in Fig. 11.
Out of the great power of LA, the SA and RA which are close to LA are influenced by the thermal effect of LA, i.e.,after the PI of LA occurs, the thermal stress that SA and RA are exposed to will decrease. Brake pad B1also has some PI effects on B2,and moreover,after B1fails,the friction stress and the thermal stress that B2experiences increase rapidly.
4.2. Generation of BDD model for system structure
It is considered that in mountainous areas, LA doesn’t work,so its system configuration in phase II is different from the other two. In this case, the system can only be reliable if all phases of mission are successfully completed. Therefore, the BDD models of different phases should be connected according to logic OR method.
According to the method in Section 3.1, after replacing the FDEP gates with logic OR gates in Fig.11,the BDD model of system structure in three phases can be obtained.
4.3. Generation of BDD model for components
FMMEA is used to determine the potential FMs of components in different phases. Besides, with the assistance of expert’s experience and database about FMs, the correlations among FMs, FM type, and etc. are determined and listed in Table 3.
In Table 3,HCI is hot carrier injection,VF is vibration fatigue, TF is thermal fatigue, EM is electrical migration, and TDDB is time-dependent dielectric breakdown.In the 3rd column,O represents O-type FMs,E represents E-type FMs,and C represents C-type FMs. Considering the FM types, the degradations of SAf3, RAf3, B2f1, and B2f2are thought to be influenced by the PI effects of LA and B1.
According to PPoF method [31,38], the distributions of FMs’ TTFs before and after the PI effect are obtained, and the results are shown in Table 3. For the FM affected by the PI effect, the mark(’)added to the FM symbol is used to represent the FM suffering the stresses after PI effect occurs.
According to the modeling methods illustrated in Section 3.2,the FMT models of all components can be generated,and then transformed into BDD models.Take B2as an example,and the FMT and BDD models of B2are shown in Fig.12.
The reliability of component A independently affected by B2f1can be obtained with Eq.(15)and Eq.(17),which is illustrated in Fig. 13 (a).
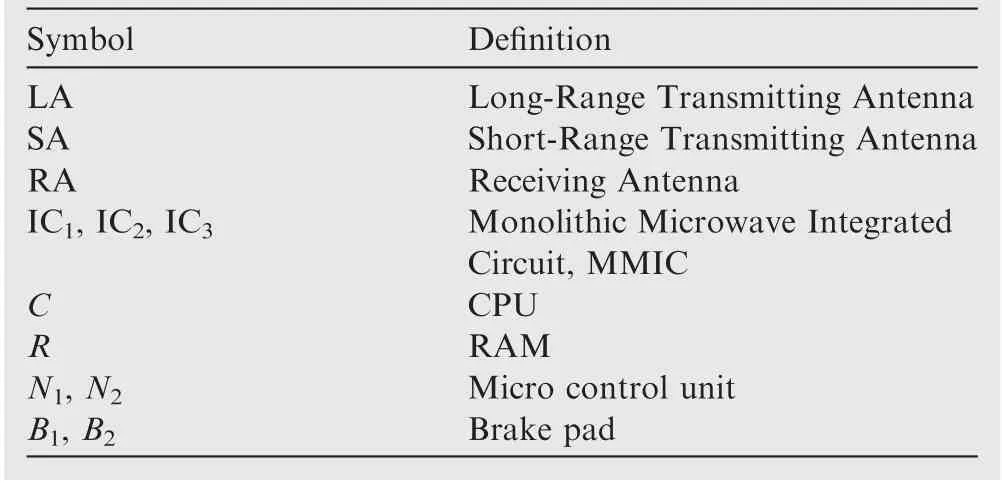
Table 2 Definitions of the symbols in Fig. 11.
In order to show the effect of the physical isolation on B2f1,this paper analyzes the failure behavior of B2f1when physical trigger component B1fails at t = 3500 h, which is labeled as dotted line with ‘△’ in Fig. 13 (a). From two dotted lines in Fig. 13 (a), we can see that after B1fails, the reliability of B2decreases much faster.The reason for this phenomenon is that after B1fails,there is only B2for accomplishing the mission to brake the UAV, and the friction stress that B2experiences increases rapidly, leading to faster degradation. So, the actual reliability of B2(labeled as solid line)is lower than the reliability without considering the PI effect. Besides, out of the more serious stress conditions, the reliability of B2in phase II decreases much faster than it in phase I. The same trend of B2independently affected by B2f2can also be found.
Then,after traveling all the paths in Fig.12(b),the reliability of brake pad B2is shown in Fig. 13 (b). After B1fails, the friction stress and thermal stress increase in some degree, so the reliability of B2decrease faster like it independently affected by B2f1, causing the actual reliability is lower than it without consideration of PI effect.
Because of the cumulative damage relation between SAf2and SAf3, this paper takes their combination SAf23as an object. In order to show the effect of physical isolation on SAf23. Similar to B2, the reliabilities of SA independently affected by SAf23and affected by both SAf23and SAf1, are shown in Fig. 14.
From two dotted lines in Fig.14(a),it can be seen that after LA fails at t = 3500 h, the reliability of SA (labeled as ‘△’)increases slightly in phase II, and increase a lot in phase III.This is because the PI effect caused by LA leads to the decrease of temperature around SA, thus slowing down the development speed of SAf3and its combination SAf23. So, the actual reliability of SA(solid line in Fig.14(a))is higher than the reliability without considering the PI effect. The similar influence and change of the failure behavior of SA affected by both SAf23and SAf1are illustrated in Fig. 14 (b).
4.4. Failure behavior analysis
After constructing the BDD models of the system structure and components, the BDD model of the whole system can be obtained with the method introduced in Section 3.3. By traveling the paths in the BDD model leading to sink node‘0’, the reliability of some subsystem and the entire system can be obtained. Fig. 15 (a) and (b) shows the reliabilities of the brake and the radar subsystem respectively.
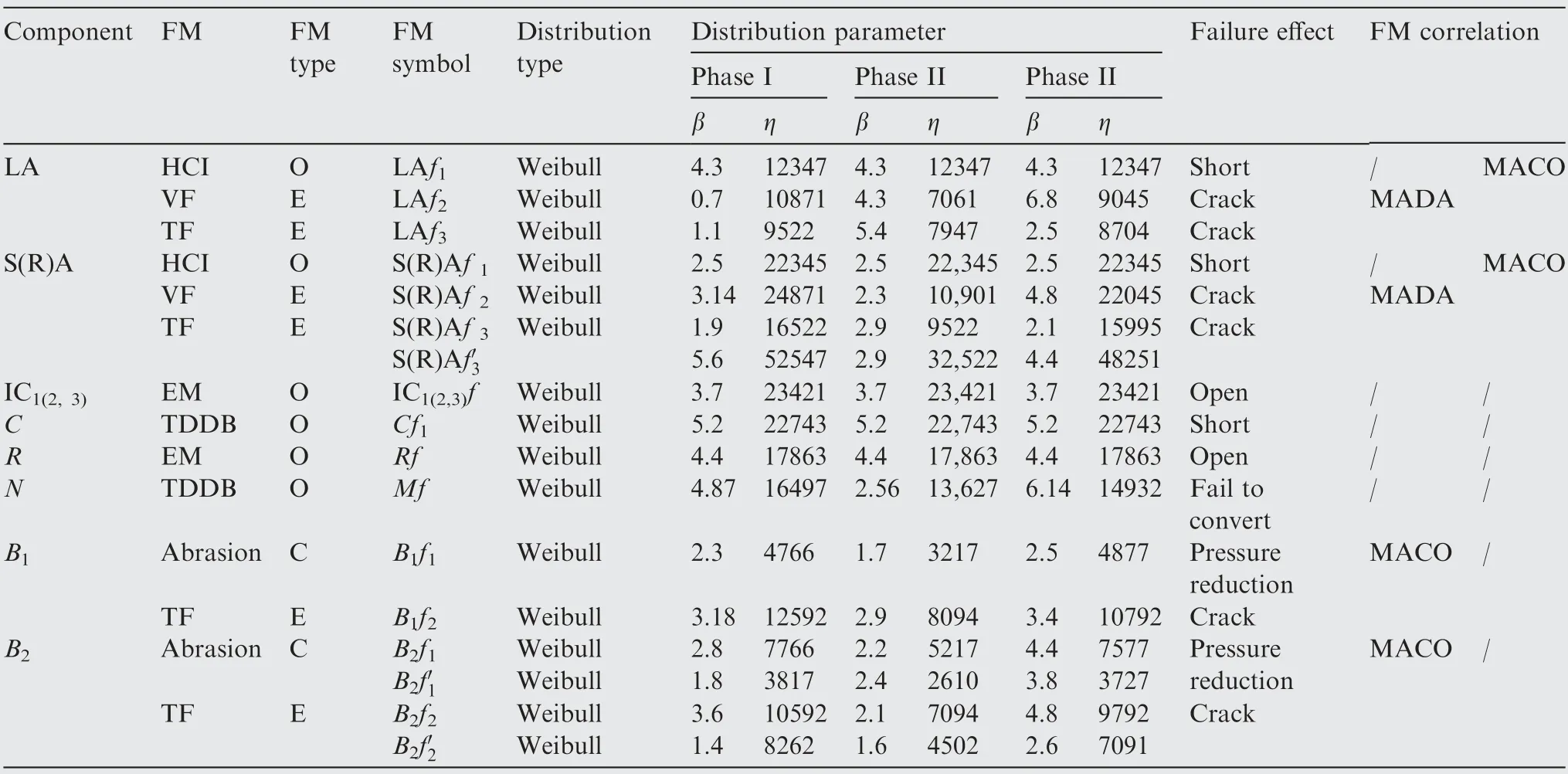
Table 3 Failure mechanisms, types, correlations, and lifetime distributions.
For analyzing the PI effect of a component on the system’s failure behavior,the reliability of collision avoidance system in Fig. 11 when B1fails at t = 3500 h is shown in Fig. 16 (a).
From Fig. 16 (a), we can see that, because of the failure of B1, the system’s reliabilities have fallen rapidly at t = 3500 h.Before t=3500 h,the reliability of the UAV’s collision avoidance system considering the PI effect is higher, which is because the PI effect of LA makes the radar subsystem’s reliability bigger than it without PI effect like Fig.15(b).But after t = 3500 h, even though LA’s PI effect still exists, but the physical isolation caused by the failure of B1accelerates the degradation of the brake subsystem, leading to a much faster decrease,which results in a lower reliability than without considering the PI effect after t = 4000 h.
For comparing the proposed method to the existing methods that only consider the functional isolation of the trigger components in FDEP groups,Fig.16(b)illustrates the failure behaviors of the collision avoidance system when N1, the trigger component in one of the FDEP groups,fails at t=1500 h.
According to the solid line and the dotted line in Fig.16(b),when the functional trigger component N1fails at t=1500 h,the reliability of the whole system decreased a little, which is not only because of its local failure, but also the B′
1s being functional isolated from the system by N1. Before B1fails at t=3500 h,for LA’PI effect,the reliability of the entire system is totally higher than the reliability without PI effect, just like the reliability before t=3500 h in Fig.16(a).If B1doesn’t fail at t=3500 h(illustrated as the dotted line with‘△’in Fig.16(b)),the reliability of the collision avoidance system will always be greater than it without PI effect. But after B1fails at t=1500 h,the actual reliability(the solid line)decreases very quickly, and after nearly t = 4000 h, the actual reliability is smaller than the reliability without consideration of PI effect,which is because that B′1s failure speeds up the degradation of B2.
Finally, the reliability of the case is shown in Fig. 17.
From Fig. 17, in phase I and partial phase II, before t = 3000 h, the reliability considering PI effect is greater than the reliability without PI effect, while after t = 3000 h, it’s totally contrary. The reason for these analytical results is that before t=3000 h,LA is more likely to be failed than B1,causing degradations of SA and RA in a lower speed. But after t = 3000 h, out of the failure of B1getting more probable,the PI effect of B1is more likely to occur and B2deteriorates faster.
So, with this case study, we know that different kinds of physical isolation effect may produce variable influences on the PMS’s failure behavior, which need to be carefully analyzed through the proposed method for obtaining a more practical result of the system’s reliability.
5. Conclusions
For modeling and analytical methods about phased-mission systems, some papers integrated the acceleration factors into the cumulative failure probability formulas for considering the across-phase damage accumulation, while many papers just assume the damages between phases are s-independent.
In this paper, we not only take the linear damage accumulation of failure mechanisms among different phases into consideration,but also analyze the physical isolation effect on the degradation and accumulations of FMs.
The proposed BDD-based modeling method is hierarchical,and it is easy to implement the three-step modeling process.Unlike those wildly-applied methods for PMSs operating complex phase algebras during constructing BDD models,we connect all the BDD models of system structure in different phases directly according to their logic relations, and leave the phase algebra operation in later analytical process.
In the case study,we use the collision avoidance system of a UAV as an example to illustrate the proposed analysis method. The results show that with different functions and stress conditions of components, the PI effects may accelerate or slow down the development speeds of O- or E-type FMs,leading the degradation of components and the system’s failure behavior more complex.
Future studies may concentrate on the non-linear accumulations among across-phase damages of phased-mission systems. Moreover, some complex situations, such as that a component is physical trigger and physical dependent component at the same time, or that a component is influenced by multiple physical trigger components, should also be further studied.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was funded by the National Natural Science Foundation of China (Nos. 62073009 and 61573043).
 CHINESE JOURNAL OF AERONAUTICS2022年10期
CHINESE JOURNAL OF AERONAUTICS2022年10期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Full mode flight dynamics modelling and control of stopped-rotor UAV
- Effect of baffle injectors on the first-order tangential acoustic mode in a cylindrical combustor
- Experimental study of hysteresis and catastrophe in a cavity-based scramjet combustor
- Flow control of double bypass variable cycle engine in modal transition
- Effects of chemical energy accommodation on nonequilibrium flow and heat transfer to a catalytic wall
- A reduced order model for coupled mode cascade flutter analysis
