Analytical redundancy of variable cycle engine based on variable-weights neural network
Zihao ZHANG, Xianghua HUANG, Tianhong ZHANG
Jiangsu Province Key Laboratory of Aerospace Power System, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
KEYWORDS Analytical redundancy;Degradation;Multiple variables;Neural networks;Variable cycle engine
Abstract In this paper, variable-weights neural network is proposed to construct variable cycle engine’s analytical redundancy, when all control variables and environmental variables are changing simultaneously, also accompanied with the whole engine’s degradation. In another word,variable-weights neural network is proposed to solve a multi-variable, strongly nonlinear,dynamic and time-varying problem. By making weights a function of input, variable-weights neural network’s nonlinear expressive capability is increased dramatically at the same time of decreasing the number of parameters. Results demonstrate that although variable-weights neural network and other algorithms excel in different analytical redundancy tasks, due to the fact that variableweights neural network’s calculation time is less than one fifth of other algorithms, the calculation efficiency of variable-weights neural network is five times more than other algorithms. Variableweights neural network not only provides critical variable-weights thought that could be applied in almost all machine learning methods,but also blazes a new way to apply deep learning methods to aeroengines.
1. Introduction
Analytical redundancy can be used to provide reference signal for diagnostics or reconstruction signal in fault tolerance control. Analytical redundancy is usually defined as signal calculated by algorithms or methods rather than signals measured by physical sensors. For example, on the premise of having installed mass flow sensors and pressure sensors at entrance and exit of compressors,when aeroengine’s rotation speed sensor gets failed, then by interpolating compressor’s characteristics map using mass flow and pressure ratio, rotation speed could be identified uniquely. Rotation speed signal calculated by interpolation is rotation speed analytical redundancy. For diagnostics, analytical redundancy could be used as reference signal to vote whether faults occur.1In fault tolerance control,analytical redundancy could be used as alternative feedback signal of fault sensors so that the close loop of control system can keep intact and finish control task.2
The interpolation method mentioned in the first paragraph is the most classical, primitive and original method to get analytical redundancy. The advantage of this method is reliable and simple to use, but its disadvantage is also manifested─limited to characteristics maps. Aeroengine’s components characteristics maps are plotted when aeroengines operate in steady status. For example, when rotator speed of aeroengines dramatically increases or decreases, aeroengines’dynamic working points do not exist in steady characteristics maps. Therefore, dynamic analytical redundancy cannot be provided in dynamic process.
To break through the limitation of steady status, scientists and engineers replace aeroengines’ math model’s Newton-Raphson iteration with dynamics, like volume dynamics,3rotor dynamics4and multibody dynamics,5by which means not only the calculation speed is drastically increased but also the simulated dynamic process gets more approximate to the real physical process. Theoretically, with the help of dynamic models, as long as entrance conditions and control variables are ascertained,all status parameters like rotation speed,pressure ratio, and temperature could be acquired, no matter in steady status or dynamic process. However, in practice, even if the principle of similitude has functioned a lot, when aeroengines operate in different working points,6a new set of modification coefficients have to be applied to aeroengines so that model’s nonlinear characteristics could keep consistent with actual aeroengines.The process of acquiring and applying sets of modification coefficients to models is usually known as model modification.7Model modification does address the problem of constructing dynamic analytical redundancy within a wide working range, but a new problem brought by these coefficients is numerous modification coefficients to be ascertained manually. Other model-based derivative methods, like Kalman filter and extended Kalman filter,8also suffer from these to-be-ascertained modification coefficients.
Manually adjusting a vast amount of parameters is a great burden to engineers, so a question is raised─could all parameters get adjusted automatically? This question is exactly the core thought of machine leaning─automatically adjusting parameters.
Numerous machine leaning methods have been proposed to construct analytical redundancy, representatives of which are Support Vector Machine (SVM) and Extreme Learning Machine (ELM). Zhao and Sun proposed an SVM to construct analytical redundancy.9By adopting greedy stagewise and iterative strategies, the SVM is capable of online estimating parameters of complicated systems. Zhou et al. proposed an ELM to construct analytical redundancy for sensor fault diagnostics.10By selectively updating output weights of neural networks according to prediction accuracy and norms of output weight vectors, the prediction capability of the ELM is enhanced.
However,it can be seen that whether in Zhao’s experiments or Zhou’s simulations, the harshest situation is dynamic process only involving three control variables, with two components’ degradation, and always at 0 height and 0 Mach number. A question is naturally proposed─why don’t these methods consider more control variables,more points in flight envelope, and the whole engine’s degradation? It is because SVM and ELM belong to shallow learning methods, a category of methods that do not have enough nonlinear expressive capability, which also explains why most shallow learning methods have to be online or onboard, because their parameters have to be updated to adapt to aeroengine’s nonlinear characteristics at different working points. From the perspective of changing parameters, shallow learning methods are not different with model modification, but it can be observed that the key point to construct strongly nonlinear systems’analytical redundancy is increasing algorithms’ nonlinear expressive capability.
Deep learning algorithms are exactly the production of solving strongly nonlinear problems, and their representatives are Long Short Time Memory neural network (LSTM) and Convolutional Neural Network (CNN). LSTM is a method that takes advantage of forget-and-memory gates to decide that sequence data at which moment should be assigned greater weights, which is the main source of its nonlinear expressive capability.11Nevertheless, the mechanism of forget-and-memory gates narrows the application field of LSTM to sequence problems,like natural language processing,
where input is a row vector. CNN originates from image processing problem, but is widely used in language processing,object detection, classification and regression. This is because CNN could incorporate almost all nonlinear layers, like activation, normalization, pooling, or even LSTM, which means that its topological structure could be extremely complicated.Exactly relying on complex topological structures, CNN can express complex system and solve strongly nonlinear problems.12Yet, the subsequent problem is the huge amounts of parameters and slow calculation speed, which is unacceptable to objects with requirement of real-time calculation, like aeroengines.
Naturally, a question is proposed: how to increase algorithms’ nonlinear expressive capability at the same time of decreasing parameters?For now,the answer could be pruning methods,13graphic CNNs,14or parameters’ dimensional reduction,15but thinking more deeply, what is the key factor to determine an algorithm’s nonlinear expressive capability?The answer to this question could be the key to unlock the contradiction between huge amounts of parameters and nonlinear expressive capability.
This paper offers a new perspective to explore the nature of nonlinear expressive capability. Inspired by a simple phenomenon, that is for a simple function f(x)=x2, if rewriting the function into f(x)=w(x)·x+b, which is the basic form of neural networks, it can be found that, when b=0,w(x)=x, the function could be perfectly fitted. However, by checking all neural networks, after training, weights are constants instead of a function of input.Thus,we generalize an idea that making weights a function of input might be the key factor to improve algorithms’nonlinear expressive capability.
This paper is organized as follows.In Section 2,Section 2.1 gives the definition of symbols and operations used in this paper, and Section 2.2 introduces the structure of Variable-Weights Neural Networks (VWNNs) and the core algorithm- variable-weights algorithm. In Section 3, experiments are conducted to demonstrate the performance of VWNN. In order to make analytical redundancy based on VWNN more convincing and compatible with milder situation, the experiment object is chosen as Variable Cycle Engine (VCE), and the experiment situation is that all environmental variables and control variables change simultaneously, also accompanied as the whole engine’s degradation. Section 3.1 is a brief introduction to VCE and data set.Steady and dynamic performance of VWNN is demonstrated in Section 3.2 and 3.3 respectively. Section 3.4 compares calculation efficiency between VWNN and other methods. Section 4 concludes the paper briefly.
2. Method
2.1. Definition of symbols and operations
Throughout this paper,research objects involve arrays of different dimensionality. Consequently, we refer to one-dimension arrays as vectors, two-dimension arrays as matrices, and three-dimension arrays as tensors.Bold lower-case letters(e.g.a)denote vectors,column vector by default.airepresents the element of a at i row.Bold upper-case letters(e.g.A)are matrices,and calligraphic bold upper-case letters(e.g.A)are tensors.
The first dimension of all arrays is row, the second dimension is column, and the third dimension is page. Besides, for convenience of transforming the algorithm into codes, getting replicated and accelerating calculation,all formulas are finally transformed into operation among vectors, matrices and tensors by using operation defined below.
Operators ‘‘.+” ‘‘.-” ‘‘.×” ‘‘.^” denote operation by element. If dimensions of two arrays do not match, the lowdimension array will be expanded into higher dimension by being replicated following the lost dimension, as shown in
2.2. Algorithm
As shown in Fig. 1, VWNN includes a core algorithm—vari able-weights layer,and accessory algorithms—input layer,output layer and feature separation layer. Before formulas, it is noted that, during forward propagation, input of every layer is output of former layer. For back propagation, output loss of each layer is input loss of latter layer. For example, output loss of activation layer is input loss of variable-weights layer.
(1) Input layer normalizes input data maps as follows to make VWNN get better converging performance.
where X is input data map sizing (m,n), μ is a column vector whose row elements are row mean values of X row, and σ is a column vector whose row elements are row standard deviation of X,and no element of σ equals zero. Y is output data map sizing (m,n).
(2) Activation layer functions as introducing activation function. In this paper, considering the good performance of LeakyReLU, it is used as activation function.16
where X is input data map sizing (m,n), W is weights matrix sizing (m,n),b is a bias vector sizing (m,1), and y is an output vector sizing (m,1).
The back propagation of feature separation layer is shown as
where lyis output loss,lxis input loss,X is the input matrix of feature input layer, DWis gradients of weights, dbis gradients of biases, and η is learning rate.
(4) Variable-weights layer makes weights a function of input so that the algorithm could get stronger nonlinear expressive capability. Theoretically, due to the fact that variable-weights algorithm is a mapping relationship from input to weights, it can be used in all weightsrelated operation, such as fully connected layer, LSTM and convolution layer.
Considering that any input array could be transformed into a vector, without the loss of generality, this paper studies the situation where input and output are all vectors. Forward propagation proceeds as the following formulas:
where x is input vector(m,1),V is variable-weights tensor sizing (m,n,m), W is weights matrix (m,n), B is bias matrix(m,n), o is offset vector (n,1).
As shown in Eq.(14),W(x)is the mathematical description of the variable-weights thought,where W(weights)is the function of x(input). Eq. (15) is the specific nonlinear relationship from x to W. Instead of updating weights, V is updated by back propagation using Eq. (16) demonstrated below.
Back propagation is shown as follows. Since weights are decided by variable-weights tensor, W does not need to be updated.
where DVis gradients of variable-weights tensor, DBis gradients of biases, and dois gradients of offset biases.sum(· , [2,3]) means getting summary along the second and the third dimension of a tensor, which means after sum(· , [2,3]), a tensor will become a vector.
To make it easier and more friendly to readers, a graphic back propagation of lx(Eq. (22)) is made as an example, as shown in Fig. 2.
(5) Output layer defines loss function as
3. Experiments, results and discussion
3.1. Brief introduction about experiment object
The basic structure of variable cycle engine and design point’s parameters are the same with Aygun and Turan’s paper.17Yao et al.’s volume dynamics is applied in variable cycle engine’s modeling of this paper.18Limited by space of this paper, a brief introduction to variable cycle engine and data set used for training, validation and test is given.
Fig.3 is VCE structure diagram.Main components of VCE include Inlet (Inl), Fan (Fan), Core Driven Fan (CDF), High Pressure Compressor (HPC), Combustion (Cbt), High Pressure Turbine (HPT), Low Pressure Turbine (LPT), Mixer(Mix), Nozzle (Noz) and Bypass (Bps). Besides, Mode Switch Valve (MSV), Forward Variable Bypass Ejector (FVBE), and Back Variable Bypass Ejector(BVBE)are used to change flow area.
Degradation coefficients are defined as
where Dcom,˙mand Dcom,erepresent component’s degradation coefficients for mass flow and adiabatic efficiency respectively;˙mcom,degradationis a component’s mass flow after degradation and ˙mcom,nominalis nominal mass flow before degradation;ecom,degradationis a component’s adiabatic efficiency after degradation and ecom,nomimalis nominal adiabatic efficiency before degradation.
In this paper, ten degradation coefficients are defined and act on VCE simultaneously─Dfan,˙m, Dfan,e, Dcdf,˙m,Dcdf,e,Dhpc,˙m,Dhpc,e,Dhpt,˙m, Dhpt,e,Dlpt,˙m, Dlpt,e. Their ranges are all from 0.96 to 1.
Original data set sizing 27×100000 includes multi-variable dynamic degrading simulation data of VCE. There is one row of time series with interval of 0.02 s, 2 rows of environmental variables (H,Ma), 5 rows of control variables(Wf,A8,Msv,ope,Fvbe,ope,Bvbe,ope) and 19 rows of state variables(T1,P1,T2,P2,T21,P21,T22,P22,T7,P7,T8,P8,P5,T6,Nl,Nh,P3,T5,P6).All variables are listed in Table 1.Rows from 2 to 22 are used as input data.Nl,Nh,P3,T5,P6are variables to be estimated.In this paper, we only take three typical signals’ estimation as example,that is Nl,P3,T5.In order to verify the basic feasibility of the proposed method, the effects of Cdf stator angle,Hpc stator angle, and turbine guide vane angle are all neglected to simplify the problem, which will be researched in further study.
Input data maps are made into 21 × 9, which includes 21 features (Rows 2-22) and 9 continuous moments (t-8,t).Moment t is the estimated moment.Considering that the problem to be solved is a dynamic problem, more than 1 moments are needed.9 moments are chosen as empirical value,which is a trade-off between inertia of VCE and fluid’s speed. Of course, 7,8,10,13 or other number of moments could be chosen,and they can also achieve similar effects.In machine learning field, parameters like the number of moments are called hyper-parameters, and the choice of hyper-parameters is still an open question. Due to the fact that the choice of hyperparameters is not the focus of this paper, we will not study the empirical value in detail.
During the process of collecting data,2 environmental variables, 5 control variables and 10 degradation coefficients vary as
where iuand idare upper bound and lower bound of variables and coefficients,c(t)is a factor ranging from 0 to 1,and o(t)is the value of variables and coefficients at time t.
c(t)is a periodical function as shown in Eq.(28),including sinusoidal signal, slope signal, and step signal. Besides, in order to make the process more complicated and challenging,periods of control variables (T) are chosen as prime numbers,as shown in Table 2.
For actual life cycle of aeroengines,degradation coefficients will not change as fast as shown in Table 3,19but considering that there are many uncertainties that cannot be reflected by math model, we decide to make degradation coefficients change more violently to balance those factors. Also, we believe overcoming a harsher situation would make VWNN more convincing and compatible with easier situations.
Fig. 4 illustrates how to segment original data map sizing 27 × 100000 into input data maps sizing 21 × 9 and corresponding output Nl. tm9is current moment, tm1is initial moment of input data maps, and Nl(23rd row, tm9) is corresponding output. With the window that includes input data maps and corresponding output sliding alongside time direction, 99992 input data maps are made. Actually Nl, P3,T5share the same input data maps. The only difference in the training, validation and test among the three variables is that the output should be altered with another variable, for example, altering Nlwith P3.
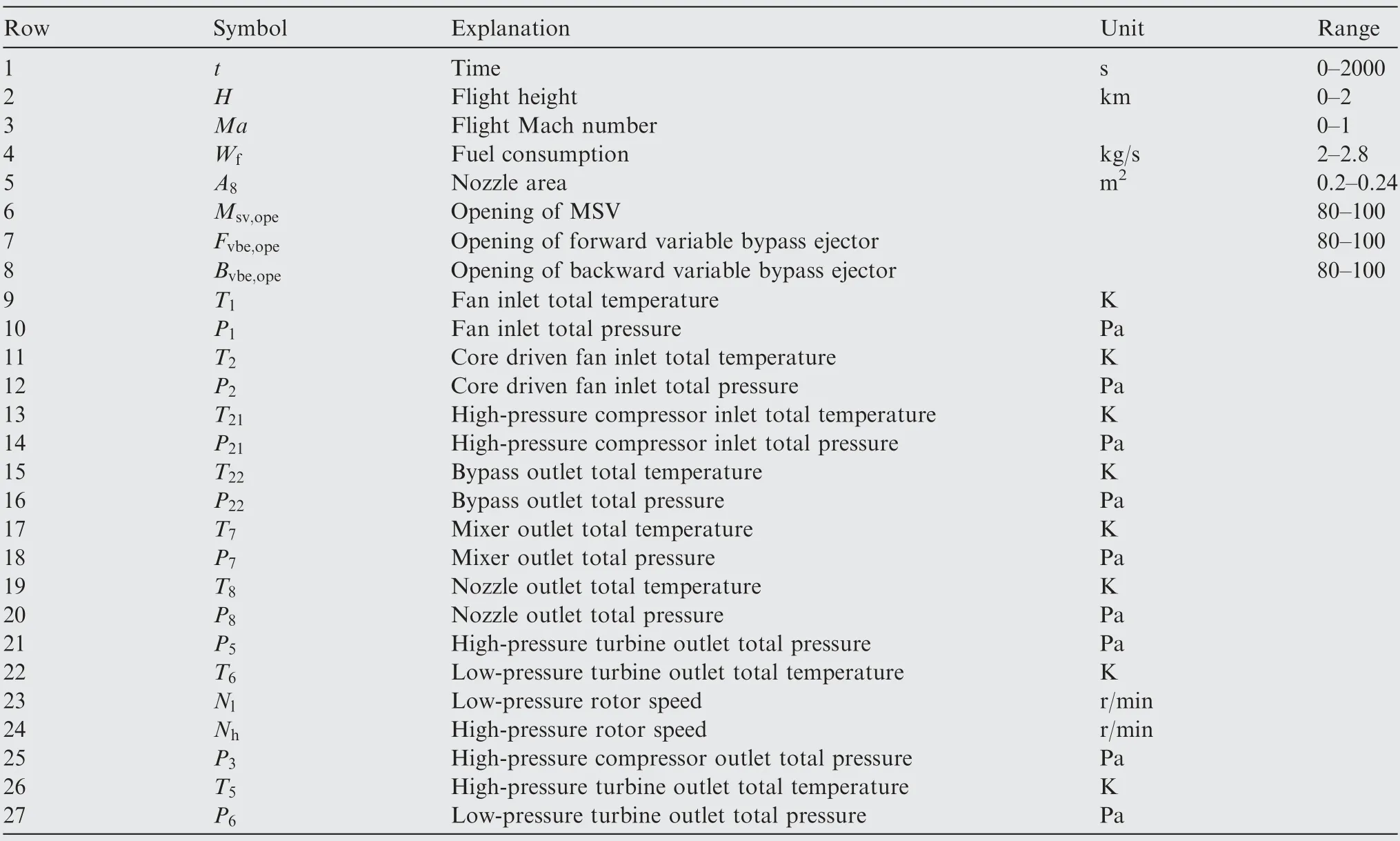
Table 1 Explanation of symbols in original data set.
For example,21×10000 data map could be segmented into 99992 data maps sizing 21×9,but in order to increase the generalization capability of the proposed method, only 90000 maps are stochastically chosen and used to train, validate and test the proposed method. 70000 input data maps are stochastically chosen and used to train VWNN, 10000 input data maps are stochastically chosen and used to validate,and 10000 input data maps are stochastically chosen and used to test.To be noted,data maps for training,validation and test are continuous respectively, which means, for example, 10000 data maps for test representing 10000 continuous moments.
3.2. Steady performance of VWNN
As shown in Table 4 and Table 5,10 steady points are stochastically chosen to validate steady performance of VWNN. Different to Section 3.1 where all control variables,environmental variables and degradation coefficients are always changing,this experiment is aimed at validating steady performance of the proposed algorithm,so the test data maps are not actually segmented from the 21 × 100000 data map mentioned in Section 3.1. Actually, by setting control variables, environmental variables and degradation coefficients as shown in Table 4 and Table 5, status parameters, like pressure and temperature,could be sampled from variable cycle engine mathematical model. After that, by combining control variables, environmental variables and status parameters, one 21 × 1 data map corresponding to one steady point could be made.Finally, in order to adapt to the input size of VWNN, the 21×1 data map is replicated for nine times alongside the time direction so that the steady data map sizing 21 × 9 could be acquired. Ten steady points correspond to ten 21 × 9 steady data maps. Besides, due to the existence of step signals as shown in Eq. (28), original data maps include many steady processes,which is why the proposed method could be applied to steady process.
In practice,degradation coefficients will follow certain natural law,and control variables are also constrained by control law, which means that there is dependence between variables and degradation coefficients. However, when components fail or meet harsh conditions, the dependence is no longer valid,like accelerating degradation or the surge of compressor. In these situations, statistical distribution of theses variables will change. In another word, statistical distribution of variables and degradation coefficients tend to be independent and stochastic. In Table 4 and Table 5, all variables and degradation coefficients are sampled randomly and subjected to Gauss distribution. Other distributions can also be used, but that is not the focus of this paper.

Table 2 Periods of environmental variables and control variables.

Table 3 Periods of degradation coefficients.
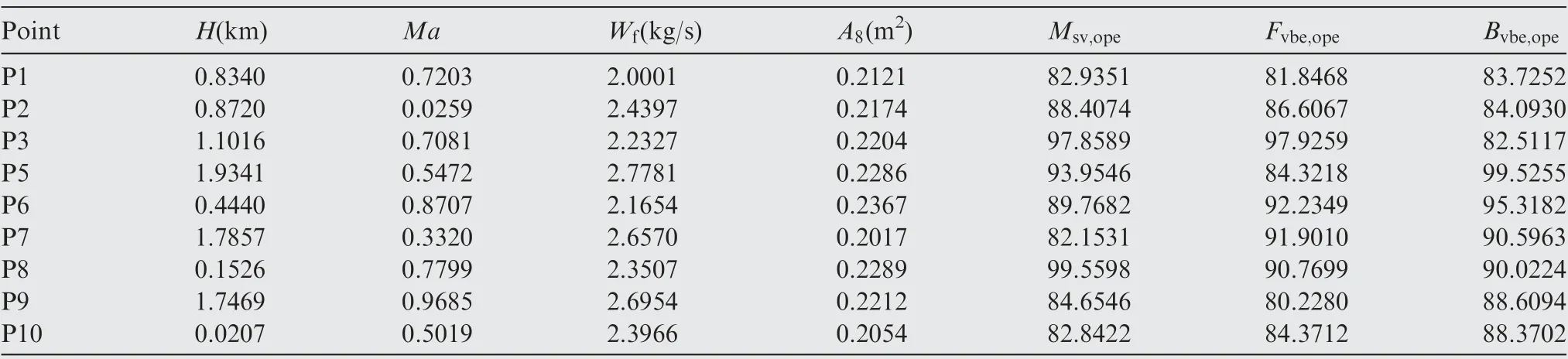
Table 4 Values of environmental variables and control variables of 10 steady points.
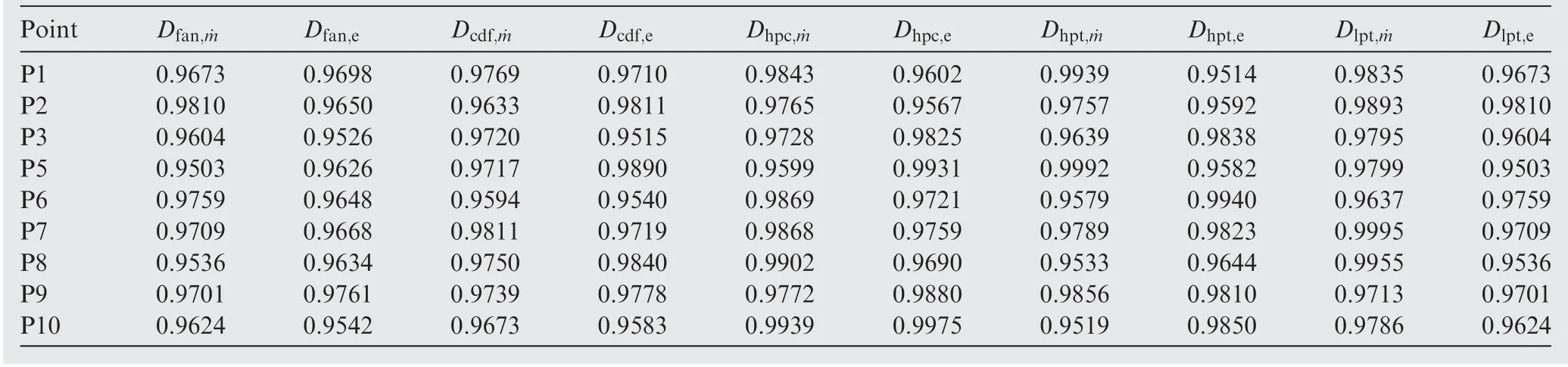
Table 5 Values of degradation coefficients of 10 steady points.
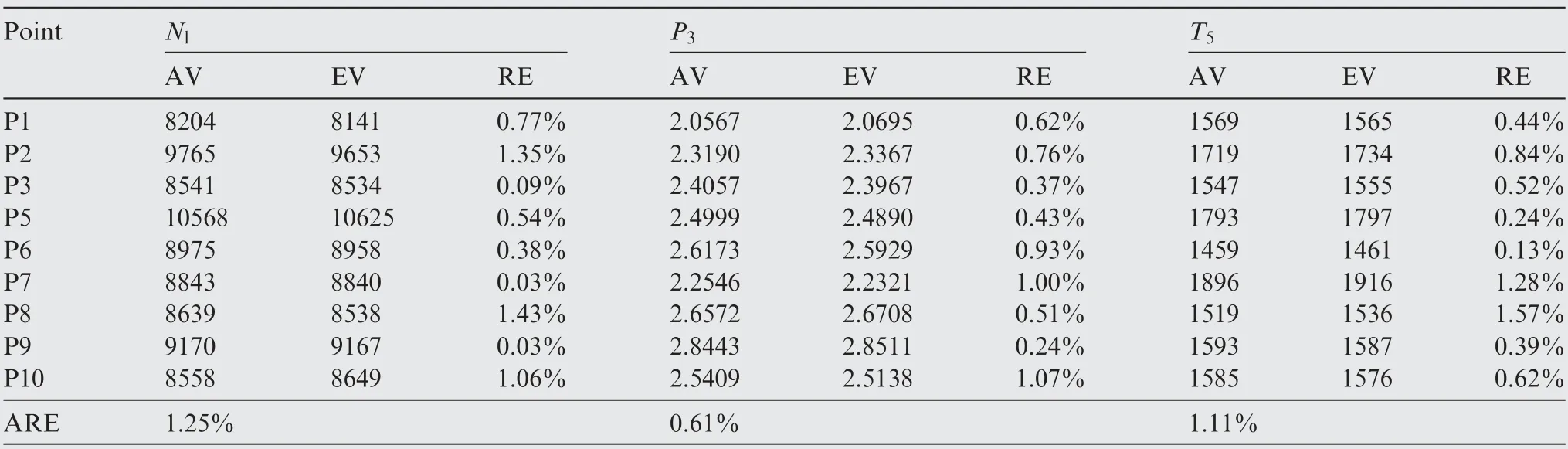
Table 6 Analytical redundancy of Nl,P3,T5 based on VWNN at 10 steady points.
AV stands for actual value,and EV is estimation value.RE means relative error,which is defined as Eq(29).ARE is average value of all relative errors. R. denotes results, and D.denotes discussion.
R.Table 6 demonstrates analytical redundancy of Nl,P3,T5based on VWNN.It can be seen that VWNN performs best in P3estimation with 0.61% ARE, while less accurate in Nland T5with 1.25% and 1.11% ARE respectively.
D. Under condition that ARE is smaller than 1.5%, it can be assumed that analytical redundancy based on VWNN is effective and satisfactory. The method to further lower ARE could be combining variable-weights algorithm and CNN, by which way network’s nonlinear expressive capability might be stronger. As for why steady performances of analytical redundancy based on VWNN between Nl,P3,T5are different,the most possible reason is that the complexity of mapping relationship from input to Nl,P3,T5is different.
3.3. Dynamic performance of VWNN
In this section, we will compare dynamic performance of analytical redundancy based on VWNN,mobile net and dense net with test data set mentioned in Section 3.1. Mobile net is a lightweight neural network owning 153 layers and usually used in lightweight devices like mobile phones and automobiles.20The amount of dense net’s layers reaches up to 709, and its mainly application situation is where higher accuracy is required with less consideration of calculation speed.21Mobile net is typical of the balance between calculation speed and nonlinear expressive capability, while dense net pursuits extraordinary nonlinear expressive capability but basically neglects the effect of large amounts of parameters. In Figs. 5-7, actual value refers to data from test data, and estimation value is analytical redundancy offered by variableweights neural network.10000 test data maps used in this section are data maps segmented from original data map as mentioned in Section 3.1.
R. Figs. 5-7 are dynamic performance of Nl,P3,T5analytical redundancy based on VWNN,mobile net and dense net.In Fig.5, it can be seen that Nlanalytical redundancies based on mobile net and VWNN are similarly accurate, both of which are more precise than dense net, but Nldynamic curve based on dense net is smoother and less oscillating. Fig. 6 shows the results of P3analytical redundancy. All three nets’ estimation accuracy is in little difference.What Fig.7 demonstrates is dynamic performance of T5analytical redundancy.Obviously,dense net is the most accurate algorithm,followed by VWNN,with mobile net taking the last position.
R. Generally comparing Figs. 5-7, we can see that VWNN performs best in P3estimation,and demonstrates similar accuracy in other two tasks. Mobile net also performs best in P3estimation, but its accuracy for Nlestimation is obviously higher than that for T5. Although the accuracy of dense net is acceptable in Nlestimation, its performances in other two tasks are relatively better, especially in T5estimation where dynamic performances of VWNN and mobile net are unsatisfactory.
D. Differences in dynamic performance among Nl,P3,T5based on VWNN, mobile net and dense net could result from the complexity of the mapping relationship from input to output and each net’s nonlinear expressive capability. For example, dense net with the most layers generally performs better than the other nets,which testifies the effectiveness of complex topological structures in nonlinear expressive capability.
3.4. Comparison of calculation efficiency

Table 7 Training time, layers and calculation speed of VWNN, mobile net and dense net.
R.Table 7 compares three nets’training time for 6 epochs with batch size 128─Training time, the number of layers─Layer and calculation speed of every forward propagation─Sc. It can be seen that VWNN is the most compact algorithm with only 5 layers, 6 min for training and 3 ms for each forward propagation. Compared to the most complex net─dense net,three indicators of VWNN are dozens of or even hundreds of times less than that of dense net.
R. Table 8 demonstrates ARE and calculation efficiency of Nl,P3,T5analytical redundancy based on mobile net,VWNN,and dense net. Calculation efficiency Ecis defined as Eq. (30),which is used as an efficiency indicator to evaluate how much accuracy that an algorithm could provide per millisecond.

Table 8 ARE and calculation efficiency of Nl,P3,T5 analytical redundancy based on mobile net, VWNN and dense net.
D.Dense net excels in P3and T5estimation, but is less accurate in Nlanalytical redundancy. Although the ARE of dense net in P3analytical redundancy is only 0.62%,the price is huge amounts of parameters and calculation overhead around 192 ms. Obviously, as far as Ecis concerned, VWNN significantly outperforms mobile net and dense net.
D.Comprehensively considering the steady performance,dynamic performance and calculation efficiency of VWNN,it can be asserted that variable-weights algorithm plays a pivotal role in nonlinear expressive capability.
4. Conclusions
(1) From the perspective of object, variable-weights neural network is proposed to construct variable cycle engine’s analytical redundancy, which is a multi-variable,strongly nonlinear,dynamic,and time-varying problem.
(2) From the view of methodology, by making weights a function of input, variable-weights algorithm increases model’s nonlinear expressive capability at the same time of decreasing the number of parameters.
(3) Experiments and results demonstrate that steady and dynamic performances of variable-weights neural network are satisfactory, and compared to other two nets,variable-weights neural network’s calculation efficiency is five times more than that of other methods.
(4) Variable-weights neural network demonstrates best accuracy in dynamic pressure analytical redundancy with only 0.74%, while the average relative error of dynamic temperature and rotation speed analytical redundancy is around 0.6%higher than that of dynamic pressure analytical redundancy.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Nos. 51576097 and 51976089) and Foundation Strengthening Project of the Military Science and Technology Commission, China (No.2017-JCJQ-ZD-047-21).
 CHINESE JOURNAL OF AERONAUTICS2022年10期
CHINESE JOURNAL OF AERONAUTICS2022年10期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Full mode flight dynamics modelling and control of stopped-rotor UAV
- Effect of baffle injectors on the first-order tangential acoustic mode in a cylindrical combustor
- Experimental study of hysteresis and catastrophe in a cavity-based scramjet combustor
- Flow control of double bypass variable cycle engine in modal transition
- Effects of chemical energy accommodation on nonequilibrium flow and heat transfer to a catalytic wall
- A reduced order model for coupled mode cascade flutter analysis
