A novel robust aerodynamic optimization technique coupled with adjoint solvers and polynomial chaos expansion

Wei ZHANG, Qing WANG, Fnzhi ZENG, Cho YAN,*

a National Key Laboratory of Computational Fluid Dynamics, Beihang University, Beijing 100083, China

b Aerospace Times Feipeng Company Limited, China Academy of Aerospace Electronics Technology, Kunshan 215000, China

c China Academy of Aerospace Aerodynamics, Beijing 100074, China

KEYWORDS Adjoint technique;Polynomial chaos expansion;Robust design;Uncertainty analysis;Uncertainty gradient propagation

Abstract Uncertainty is common in the life cycle of an aircraft, and Robust Aerodynamic Optimization (RAO) that considers uncertainty is important in aircraft design. To avoid the curse of dimensionality in surrogate-based optimization, this study proposes an adjoint RAO technique called‘‘R-Opt”.Polynomial Chaos Expansion(PCE)is coupled with the R-Opt technique to quantify uncertainty in the responses of the target(including its mean and standard deviation).Only one process of PCE model construction is required in each iteration, and the gradients of uncertainty can be inferred via chain rules. The proposed method is more efficient than prevalent methods,and avoids the problem of a disagreement over the best PCE basis from among a number of PCE models (especially in case of sparse PCE). It also supports the application of sparse PCE.Two benchmark tests and two airfoil cases were used to verify R-Opt, and the optimal solutions were deemed to be robust. It improved the mean aerodynamic performance and reduced the standard deviation of the target.

1. Introduction

Uncertainty is widespread in the life cycle of aircraft systems.Uncertainties, due to the aerodynamic environment, aerodynamic shape, payload, engine thrust, etc., have a significant influence on the characteristics of flight and need to be considered. Robust Aerodynamic Optimization (RAO) combined with uncertainty analysis is important for the design of complex systems, such as those of aircraft. Considerable research has been conducted on RAO in light of uncertainty.1-3In RAO design, the target of optimization is expected to be minimized while being rendered insensitive to small variations in the disturbance parameters. In problems of uncertainty as described in statistical theory, the mean value of the optimal objective as well as the variance or standard deviation caused by perturbations is expected to be minimized. Other non-statistical theories for uncertainty characterization, such as fuzzy set theory4and interval analysis theory5, are beyond the research scope of this paper.

In 1998,Drela6claimed that multi-point design is defective for robust optimization because it is only locally optimal at the design points but does not perform well over the entire uncertain interval. Huyse et al.7proposed a max/min robust design method for expectation and variance in 2002,and applied it to the RAO design of an airfoil. For optimal problems with many uncertain factors, and given the high cost of real functions,Dwight and Han8performed Uncertainty Quantification(UQ) analysis by using the sparse grid technique on the Gradient-Enhanced Kriging(GEK) model in 2009 to improve efficiency and accuracy.Ryan et al.9-10examined the use of data processing methods on multi-objective robust optimization in 2014, and applied them to the robust design of rotors. Han et al.11studied the UQ method based on the Kriging model in 2016,and applied it to the RAO of a supercritical airfoil under perturbations of the Mach number and angle of attack. Bai et al.12constructed a framework for robust optimization based on the stochastic Kriging model in 2016,and performed robust optimizations on the NASA Common Research Model.In 2018,Gan et al.13optimized the conformal expansion nozzle of an unmanned aerial vehicle through the Monte Carlo Simulation(MCS) and a surrogate model of the Radial Basis Function(RBF).In a review of RAO design in 2019,Gao et al.14indicated that the MCS when used with metamodels can reduce the computational cost of UQ analysis.With regard to the optimization procedure,the GEK model can significantly enhance the accuracy and efficiency.A bilevel surrogate approach was proposed by Sabater et al.15in 2020 and applied to the robust optimization of shock control bumps. Polynomial Chaos Expansion (PCE)was verified as an efficient and accurate approach for simulating uncertainty in the conditions of manufacturing and flow by Dodson and Parks.16It has been applied to robust optimization as well.17-19

There are two key issues in RAO design.One is the technique used to quantify uncertainty under perturbations,and the other is the technique of aerodynamic optimization used.The MCS,13the PCE method19,the surrogate-based methods20-21,and their combinations19,22-23are commonly used UQ approaches in RAO in recent research.There are two main categories of aerodynamic optimization: the adjoint optimization technique24-26and the surrogate-based optimization technique27-29. Most available RAO techniques are constructed based on surrogate optimization. Therefore, the accuracy and efficiency of these techniques are limited by those of the related surrogate models.Additionally,another obstacle called the‘‘Curse of Dimensionality”is usually encountered in model construction.

To alleviate the curse of dimensionality, Tao et al.30introduced principal component analysis to model processing to reduce the number of design variables. The GEK model was developed to mitigate the risk of high dimensionality.31Researchers have also focused on the application of adjoint methods to robust problems because of their efficiency independent of the dimensionality of the design variables. Sriram and Jameson32developed a partially intrusive approach for robust optimization and applied it to the optimization of RAE2822. However, this method requires the reformulation of the adjoint solver for each PCE basis, and the implementation is challenging when the target function becomes complex.Kumar et al.33-34also attended to the combination of PCE models and adjoint solvers for robust problems. He constructed PCE models not only on the target functions but also on each gradient function obtained from the adjoint solvers.This method was successfully applied to the robust aerodynamic optimization of the NACA0012 and RAE2822 airfoils.

However, the approaches proposed by both Jameson and Kumar require that the PCE basis be the same in PCE models of the target functions, the gradient functions, and even the governing equations.In this case,an inevitable problem is that the PCE basis most suitable for one function may not be suitable for others,on account of possibly large differences in their trends of variation(i.e.,the target functions,the gradient functions, the governing equations, and the flow variables). This state worsens especially when the sparse PCE is applied. To avoid this problem, the authors examine the intrinsic law of PCE construction, and propose a new robust optimization technique called the ‘‘R-Opt” by combining the adjoint solver with the PCE model.

The proposed R-Opt method requires the construction of only one PCE model (whereas prevalent approaches require a number of PCE models)in each iteration of robust optimization. It is constructed based on the open-source code of the Stanford University’s Unstructured (SU2) tool.25The targets of optimization are the uncertain responses of the aerodynamic Quantities of Interest(QoIs),including the mean value and the standard deviation.The R-Opt technique consists of two parts.One is the non-intrusive PCE approach to quantify the uncertain responses of the target in each iteration of the optimization. In this part, inferring the gradients of the uncertain responses is important.The other part of the R-Opt technique is the adjoint solver used to access the robust optimal solution.

The remainder of this paper is structured as follows. The Computational Fluid Dynamics (CFD) numerical algorithms are outlined in Section 2, including the governing equations and equations for the adjoint solver. Section 3 reformulates the PCE approach and derives the gradients of uncertainty with respect to the design variables.The principles of Kumar’s method are also listed for comparison. The framework of the proposed robust optimization technique R-Opt is provided in Section 4. In Section 5, two benchmark functions are used to validate the performance of R-Opt. Two cases of robust aerodynamic optimization are considered using the R-Opt framework in Section 6, and robust solutions are also compared between these cases. Section 7 summarizes the paper.

2. Numerical method

The main algorithms of the governing equations and the adjoint equations are outlined below.

2.1. Governing equations

The Reynolds-Averaged Navier-Stokes(RANS)equations are used as the governing equations of flow,and are summarized in

where Ω is the computational field, S represents the surface of the aerodynamic body, and Γ∞is the far-field boundary.The first line of Eq. (1) shows the governing flow equations, where U represents the conservative flow variables,Fcshows the convective fluxes, and Fυk(k = 1,2) represents the viscous fluxes. The expressions of these variables are shown in

with ρ the fluid density, P the static pressure, T the temperature,vithe ith component of the velocity vector v,e the internal energy,H the total enthalpy,δijthe Kronecker function,cp=-γR/(γ-1)the specific heat capacity at constant pressure,and τijthe tensor component of shear stress. The other three lines in Eq. (1) represent the boundary conditions, including the noslip wall condition in line 2,the adiabatic wall condition in line 3, and the characteristic-based far-field condition in line 4. W represents the characteristic variables.

According to the Boussinesq hypothesis35,the effect of turbulence can be expressed by an increase in the viscosity term.Thus, the total viscosity consists of the laminar viscosity μdynand the turbulent viscosity μtur. In this case, μυkin Eq. (1)can be acquired by

The first line in Eq.(4)shows the equation governing turbulence.Tcυ= Tcυ(U,^ν,dS) represents the convective and viscous terms, whereas Ts= Ts(U,^ν,dS) represents the source term. dSis the distance to the body surface S,and is simulated from the Eikonal equation in Eq.(5).The other two lines of Eq.(4)are the boundary conditions. Line 2 is the viscous wall condition,

where^ν is set to zero.Line 3 is the far-field condition that implies that a certain ratio of the laminar viscosity is imposed as turbulent viscosity at the far field, where σ∞is a turbulence model constant.

2.2. Adjoint equations

In aerodynamic optimization design, the integrals of the surface force (e.g., the lift and the drag coefficients) are typically selected as the target of optimization. Those target functions(marked as J) can be written as

where ΨU= [ψ1, ψ2, ψ3, ψ4, ψ5]T,ψ^ν, and ψdare Lagrange multipliers for the governing equations RU,R^ν, and Rd.

The variation in J due to boundary’s deformation can be expressed as

Note that the variation in J in Eq. (22) is not explicitly dependent on dS. Moreover, the first two lines of the adjoint equations in Eq. (20) are also independent of ψd. Therefore,only the first two lines of Eq.(20)are considered in the adjoint systems.

For specific derivation process, the readers could refer to Refs. 25,38 for more information.

2.3. Code discretization

The equations above are discretized on an unstructured mesh.To discretize the convective fluxes of the governing equations,Jameson’s central scheme39is used along with the monotonic upstream-centered schemes for conservation laws.When computing the viscous fluxes,the gradients of the flow variables are calculated via the Green-Gauss method. The source terms are approximated via piecewise reconstruction. After spatial discretization, the implicit Euler scheme is used for time integration.

Two approaches are available (the turbulent adjoint method and the method with frozen eddy viscosity) for handling the turbulent viscosity of equations of the adjoint solver during the linearization and discretization of its models. A comparison between these methods is provided in the first part of Section 6. We used the turbulent adjoint method here. The discretization of the terms in the adjoint equations are set as the same with those relative in the governing equations.Jameson’s central scheme is used for discretization of the convective terms,the Green-Gauss method is applied for discretization of the viscous terms, and the piecewise reconstruction is implemented for discretization of the source terms and the coupling residuals.

3. Uncertainty quantification and gradient propagation

To solve the PCE system, least-squares regression is used,and the coefficient vector j of PCE is shown as The methods used to quantify uncertainty and determine the propagation of its gradient are inferred and presented in this section.

3.1. Uncertainty quantification

To measure uncertainty in each iteration, non-intrusive polynomial chaos expansion40was performed to create a stochastic model between the aerodynamic QoIs (e.g., the lift coefficient CL) and the parameters of perturbation.

In PCE construction, the target function J* can be decomposed into a series of orthogonal multivariate basis functionsφi(ξ ), i = 0, 1, ..., Nt, as shown in Eq. (30). The superscript ‘‘*” represents that there exists perturbation in J.

The series is theoretically infinite but is truncated to Nt+1 terms for implementation.ji(i=0,1,...,Nt)represent the relevant coefficients to be solved. ξ = [ξ1, ξ2, ..., ξn] is an ndimensional standard random vector, and the multivariate PCE basis φi(ξ ) is the product of the orthogonal univariate basis functions of the related stochastic parameters ξi, i = 1,2,...,n.The selection of the univariate basis function is related to the probability distribution of the corresponding stochastic parameter ξi, as shown in Table 1.

The expansion of the PCE model on Nssamples is shown in Eq.(31),where the superscripts in bracket indicate the sample index, and the subscripts represent the basis index.

Once the uncertainty in the target has been obtained, its gradients required for the adjoint solver are derived as shown below. For comparison, Kumar’s approach33,34is also outlined.

3.2. Propagation of uncertainty gradient

3.2.1. Kumar’s method

In Kumar’s method,33,34the gradient Λ*of the target function J*can also be written in PCE form,with the same orthogonal multivariate basis functions as that of the target PCE model J*, as shown in

Table 1 Relationship between orthogonal basis function and probability distribution.

However, as mentioned in Section 1, a problem may arise

whereby the basis used in the PCE models of the target function and the gradient function ought to be the same in this method. This is inconsistent with the fact that the PCE basis is usually different for different settings of model order for different problems. Moreover, the presupposition of the same PCE basis is an obstacle to the application of the sparse PCE.To solve this problem,the authors examine the construction of PCE and propose a method for the propagation of the uncertainty gradient.

3.2.2. Proposed method

In Eqs. (31)-(33), the matrix of the PCE basis Φ is associated only with the distribution of the random variable ξ and the model order. Therefore, it is independent of the value of the target function vector J＊. We denote by A the result of the matrix operation (ΦTΦ)-1ΦT, which is also independent of J＊.After that,the PCE coefficients in Eq.(33)can be rewritten as Eq. (41) and expanded as Eq. (42)

In this case, the PCE coefficients ji, i = 0, 1, ..., Ntcan be considered to be linearly weighted combinations of the values J(k)(k=1,2,...,Ns)of the target function J*at those sample points.The elements Aikin matrix A are the relevant weighting coefficients. The uncertainty in J* can be rewritten as

Once the values of the target function J* and its gradient function ∇J*(e.g., the lift coefficient CLand its gradient∇CL) at each sample point have been confirmed via the

CFD simulations in Section 2, only one process of PCE construction on the target function is required, and the uncertainty as well as the uncertainty gradient can be obtained via Eqs.(34)-(36) and Eqs. (45)-(47), respectively. This method avoids multiple PCE constructions, and is applicable to the sparse PCE. For instance, if the subset of the chosen crucial basis is denoted by C={φi′, i’=1, 2, ..., c}, the uncertainty and relevant gradients are:

where matrix A can also be obtained from the new PCE basis.

The successful implementation of this newly proposed method is based on the accurate calculation of the inverse matrix of ΦTΦ. For reliable and stable calculation, especially when the matrix scale is not large,the Cholesky decomposition method is employed.This method has been integrated in many mature techniques,such as Python and MATLAB,and is easy for the readers to get started with.When the matrix ΦTΦ is in large-scale, which indicates that the number of PCE terms is also large, the PCE model will be very complex, and the overfitting effect will possibly emerge. Besides, the curse of dimensionality will also occur. To avoid this awkward situation, the sparse PCE method will be integrated in the R-Opt technique in future works. The integration could be easily implemented on account of the features of R-Opt.

3.3. Comparison of model solutions

The PCE model in Kumar’s method is solved by employing the Numerical Quadrature Method (NQM). The number of required samples is defined as

where ptis the model order and d is the dimensionality of the disturbance considered in PCE.As d increases,the sample size of the demand increases exponentially,which is undesirable.In addition, the samples are fixed at the roots of the orthogonal basis function selected according to the disturbance distribution.

Another method typically used to solve PCE is the Least-Squares Regression (LSR), and is used here. The sample size required in this method can be defined by Eq. (53), where ndis the over-sampling rate, with a recommended value of two in Ref. 41. The samples are obtained via the Latin hypercube design sampling strategy,and are more space-filling than samples set in NQM.

The sample requirements of these two methods are compared in Table 2. It is clear that the sample requirement in LSR is quite smaller than in NQM,especially when the disturbance dimensionality is high. Moreover, the PCE prediction using LSR is more accurate in the benchmark tests reported in Section 5.

The requirement of the number of samples above is designed for ordinary PCE methods. However, when the sparse PCE is applied, it is always accompanied by the adaptive sampling strategy. The NQM is not good at handling this kind of problem while the LSR method can still work well with it.42

For the above reasons, we used LSR to solve the PCE model in this research.

4. Optimization framework

In the context of robust optimization,a new target function J’can be defined as a weighted combination of the mean and standard deviation of the original target function J*,as shown in Eq. (54). Its gradient can be obtained via chain rules, as shown in Eq. (55). The values of m and n are usually equal to 1 or 2 in common robust optimization problems.

The framework of the proposed adjoint solver-based RAO technique, R-Opt, is shown in Fig. 1. The Free-Form Deformation(FFD)technology developed by Sederberg and Parry43is employed to parameterize the aerodynamic shape. In each step of the iterations, the original and adjoint flow fields are simulated in every sample condition. The PCE approach and gradient propagation mentioned in Section 3 are implemented to obtain the uncertainty and uncertainty gradients of the target QoIs, respectively. Following this, the new target function and the gradient function of the robust optimization problem in Eqs. (54)-(55) can be acquired. The gradient optimization algorithm is then applied to iterate to the next values of the design variables. The L-BFGS-B algorithm44is used in all cases of optimization in this paper. The iterations were performed in turn until the criterion for gradient convergence in Eq.(56)was met.ε was set to 10-6.In case they exist,the constraints are appended to the target function as penalty terms,which are not specified here.

In this study,the sample set in each iteration step was set to be the same for simplicity. However, the sample sets do not have to be identical at all. The R-Opt technique also supports the application of the sparse PCE method, the application of which in each step of the iteration is independent.

5. Benchmark testing

Two benchmark functions were used to test the performance of the R-Opt optimization technique.

5.1. Test I: Perm function

The first benchmark was performed on the 2D Perm function,as shown in Eq. (57), to observe the process of robust optimization of the proposed method. The parameter β was used to introduce perturbation into the function. It was assumed to be uniformly distributed in the interval [0, 1], and was set as 0.5 in the original form of the function.

The iteration process of the R-Opt technique is shown in Fig. 2, as well as those of the deterministic optimization method (marked as ‘‘D-Opt”), the common statistical method of robust optimization (marked as ‘‘Statistical”), and the method of robust optimization proposed by Kumar (marked as ‘‘Kumar”). The common statistical method of robust optimization uses samples obtained with equal probability in the disturbance space. The uncertainty is obtained by

where w is the weight coefficient of σ, and is first set to 0.5 in this case.

A total of 100 samples (proved to be convergent by the authors, whose proof is not provided) were used to quantify the uncertainty caused by β in each iteration of the statistical method. The other two approaches were based on PCE, and both were truncated to the fourth order. The over-sampling rate was set to 1.0 in R-Opt in this part of the case, and the requirement of samples number was identical to that in Kumar’s method.

All three robust approaches were more robust than the deterministic optimization technique, and their mean values and standard deviations were smaller. In addition, although the specific PCE constructions and gradient propagations were different between R-Opt and Kumar’s method, the fourth-order PCE was accurate enough in this case, and their performances were similar.

Table 2 Comparisons of sample requirements between LSR and NQM.

The second part of this case involved a comparison of the performances of the three robust optimization techniques with new complex perturbations (αj, j = 1, 2), as shown in Eq. (60). All three perturbations are listed in Eq. (61). In the common statistical method, 100 samples were used, but in the other two PCE-based methods, the PCE model was truncated to the second order. Therefore,Kumar’s method required 27 samples and the R-Opt technique required 20, with nd= 2.

Different optimal results were obtained by changing the weight coefficient w in the target function for robust optimization.The Pareto fronts of these robust approaches are formed and shown in Fig. 3. It is clear that the optimal results of the common statistical method and the R-Opt method were similar. Besides, the optimal results of Kumar’s method were also close to the Pareto fronts of the other two methods.However,they flocked together. This implies that Kumar’s method lacked the ability to explore more possible robust solutions in this case, which is not ideal.

The differences between the predicted and the actual values of the optimal points are shown in Fig. 4. Prediction errors of the standard deviations using Kumar’s method were much higher than those of the other methods, which shows that the Kumar’s method may not be suitable for this case. For verification, 10 test points were randomly selected from the design space. The predicted uncertainty and the uncertainty gradients under disturbance are compared between these methods at the test points in Figs. 5 and 6, respectively. MCS simulations with 100,000 samples at the test points were applied as standard. The predicted mean values and the corresponding gradients of all these methods were accurate. However, these methods behaved differently for predictions of the standard deviation and the corresponding gradients.The R-Opt method was just as effective as the statistical method but required fewer samples, whereas Kumar’s method yielded large errors.

It is clear that the predictive accuracies of Kumar’s method on different functions(for the mean value,standard deviation,and gradients of the mean value and standard deviation with respect to the design variables) were different. This suggests that the best PCE orders (i.e., the best PCE basis functions)for these different functions disagreed. Before application, all of them needed to be verified, which significantly reduced efficiency.The R-Opt technique,on the contrary,encountered no such problem.

5.2. Test I: Rosenbrock function

The second case involved a multi-dimensional Rosenbrock function, as shown in Eq. (62). α, β, and γ were the factors influencing perturbation in this case. They were all assumed to be uniformly distributed in the interval [0,2], and were set as 1.0 in the original form of the function.The sample requirements of these three methods were the same as those in Test Ⅰ.

The dimension k of the function was first set to 2.By changing w, the Pareto fronts of these approaches were obtained,and are shown in Fig.7.It is clear that the results of Kumar’s method were not satisfactory. Three of the six optimal results were far away from the Pareto front of the common statistical method.Moreover,although the results of the other three tests were located on the Pareto front, they still flocked together,which is not ideal.All six optimal results of the R-Opt method were located on the Pareto front of the common statistical method.

The actual and predicted results are compared in Fig. 8.The prediction errors of Kumar’s method were higher than those of the others.

To examine the performance of these methods in the entire design space, 10 test points were randomly selected, and the uncertainties and uncertainty gradients at these points are shown in Figs. 9-10. These methods delivered similar performance, although Kumar’s method was slightly worse than the other at a few points. However, when attending to the space near the optimal solution(another 10 random test points were selected, as shown in Figs. 11-12), the results of prediction using Kumar’s method were not consistent with those of the MCS. Differences were still obtained in the accuracy of prediction among the target functions and the gradient functions, and the best PCE basis functions are still indicated different. The common statistical method performed well throughout the design space but required a large number of samples. The predictive accuracy of the proposed R-Opt technique was not as high as that of the common statistical method, but it yielded a much smaller error than Kumar’s method and required the fewest samples of all three methods.

According to the above analysis, Kumar’s method did not maintain high predicting accuracies of uncertainty and uncertainty gradients in the entire design space,especially when near the possible optimal solution. Therefore, it was difficult to obtain the optimal solution (e.g., three points away from the Pareto front in Fig. 7). However, the R-Opt technique delivered better performance.

In the second part of this case, the dimensionality of the problem was increased from 2 to 10. The optimal results are shown in Figs.13 and 14.Kumar’s method still had low accuracy of predictions near the possible optimal solution and ROpt still performed well.

6. Cases of robust aerodynamic optimization

After the benchmark tests, several airfoils were optimized to evaluate the proposed R-Opt method.

6.1. Code verification

6.1.1. Verification of aerodynamic simulation

An RAE2822 airfoil manufactured by Cook et al.45was used to verify simulations of the direct flow fields and adjoint flow fields in this study. The gradients of the design variables were also validated by comparison with those obtained via the finite difference approach.

The calculation condition for the RAE2822 is shown in Table 3, and the distribution of the pressure coefficient on the surface of the airfoil is shown in Fig. 15. We can see that the simulation agreed well with the experimental result.45

Comparisons were also made between the adjoint flow fields obtained in this study and a reference CFD simulation from Alfonso’s work.38Different adjoint flow fields are simulated for different objectives to obtain the gradients of the objective functions. The contours of the density-adjoint variable for drag and lift were simulated via the turbulent adjoint approach, and are respectively displayed in Figs. 16 and 17 along with Alfonso’s results.The flow structures of the adjoint flow fields were consistent.

To illustrate the effects of flow turbulence on the adjoint solutions, the contours of the turbulent adjoint variables are shown Fig. 18. Fig. 18(a) shows the result under the drag objective and Fig. 18(b) shows that under the lift objective.It is clear that the values of the turbulent adjoint variables under the two objective functions were nearly zero when they were far from the surface of the airfoil.However,variations in the turbulent adjoint variables were considerable near the surface of the airfoil. This led to a certain difference between the gradients predicted via the turbulent adjoint and the frozen viscosity adjoint approaches, as shown in Fig. 19.

To further validate the accuracy of calculation of the gradients, adjoint approaches (including the turbulent adjoint and the frozen viscosity adjoint approaches) and finite difference approaches (with two design variable steps of 10-5and 10-6)were employed. The gradients of the drag and lift coefficients obtained using them were compared, as shown in Fig. 19.The setting of the FFD variables is also shown in Fig. 19(a).The results of the two finite difference approaches were nearly the same, and were set as the reference. Compared with the frozen viscosity adjoint approach, the turbulent adjoint method was able to describe the gradients more accurately,and its result was more consistent with those of the referenced finite difference approaches. Therefore, it was applied to solve the adjoint flow fields and to obtain gradients of the design variables.

Table 3 Calculation condition of validation case.

6.1.2. Verification of uncertainty quantification

Before applying the R-Opt technique, we needed to verify the capability of uncertainty quantification of PCE and confirm an appropriate order. An RAE2822 transonic flow field with an uncertain Mach number was selected as the validation case.The baseline condition was set as the same in Table 3. Moreover, the Mach number was assumed to follow a uniform distribution of U(0.704,0.764). The MCS analysis and the PCE approaches with different orders were utilized to quantify uncertainty under this perturbation in the Mach number.The MCS analysis is carried out 1000 times, and its result was treated as the standard.

As shown in Fig. 20, the mean values and standard deviations of several QoIs(including the lift coefficient CL,the drag coefficient CD,and the lift-to-drag ratio K)were quantified via these methods and compared. The numbers of CFD evaluations required are listed in Table 4. It is clear that all results of the PCE approaches were within the 5% error range of the standard,and the required number of samples was significantly smaller than that in MCS.

Curves of the Probabilistic Density Function (PDF) of these QoIs are plotted in Fig. 21. They were obtained by using a kernel density estimate on 10,000 random samples simulated via the PCE models. Those of the MCS are also plotted as standard. It is clear that when the order of PCE was 4 or higher, the PDF curves were consistent with the standard.

Therefore, the fourth-order PCE model as well as its coefficient vector was confirmed to be sufficiently accurate. It was then employed in the R-Opt optimization technique to robustly optimize airfoils.

6.2.1. Case Ⅰ: RAE2822, Ma ～N(0.734, 0.012)

The first case involved maximizing the lift-to-drag ratio K of the RAE2822 airfoil. The baseline calculation condition was set as in Table 3. Disturbance was assumed on the freestream Mach number,and followed a normal distribution of N(0.734,0.012). R-Opt was executed several times under different settings of the weight coefficient w of the standard deviation.The optimal target is listed in Eq. (64), where θ represents the thickness of the airfoil. For comparison, the deterministic optimization(D-Opt)was also performed,and the corresponding target is listed in Eq. (65).

6.2. Robust optimization test

After code verification, the adjoint solver-based RAO technique R-Opt was executed to optimize two airfoils.

The optimal results are shown in Fig. 22 and Table 5. The mark ‘‘↑”/ ‘‘↓” in Table 5 indicates that the larger/lower the value of the relevant QoI, the better. All optimal airfoils were deemed as meeting the geometric constraints. The mean value μ was expected to be maximized in the optimization, and the standard deviation σ was expected to be minimized. The bottom-right corner in Fig. 22 shows the desired direction of optimization. Moreover, the coefficient of variation (cv,defined in Eq.(66))was utilized to measure the optimal results.The lower the value of cvwas, the more robust the airfoil was

When w was set to 0.1 or 0.5 in the robust optimization,the optimal airfoils dominated the original RAE2822 airfoil (i.e.,the optimal airfoils were better than the original RAE2822 airfoil). The mean value was higher and the standard deviation lower. When w was 0.9, although the mean K of the optimal airfoil decreased considerably, so did the standard deviation and the coefficient of variation. It led to higher robustness,although performance was not satisfactory. In comparison with the use of the D-Opt on the airfoil, the optimal airfoil with w=0.1 was slightly more dominant.Although the mean performance of the optimal airfoil with w = 0.5 was slightly worse, it did perform better in terms of reducing the standard deviation.Of the airfoils obtained via the R-Opt technique,the one with w=0.5 had the smallest coefficient of variation,and was selected for comparison with the deterministic optimal airfoil. This robust airfoil is called the R-Opt airfoil hereinafter for simplicity of reference.

The shapes of the airfoils are compared in Fig. 23(a). Fifty sample conditions were selected in the disturbance interval of the Mach number with equal probability, and variations in the surface pressure of the RAE2822 airfoil,the D-Opt airfoil,and the R-Opt airfoil under these conditions are compared in Figs. 23(b)-(d). The distributions of the lift coefficient, drag coefficient, and lift-to-drag ratio are compared in. Curves of the probabilistic density functions of K of these airfoils are compared in Fig. 24(d).

The shock wave on the upper surface of the RAE2822 moved backward and strengthened with an increase in the Mach number. Those of the D-Opt and R-Opt airfoils moved backward as well but were first weakened in intensity. The shock wave was gradually decomposed into two weaker ones that were recombined to form a stronger one after that. The difference between these airfoils was in the process of variation in the shock waves.The variation in the D-Opt airfoil was faster.When the Mach number was increased to the baseline condition, the shock wave on the R-Opt airfoil was still split into two while that on the D-Opt airfoil has already been recombined into one. In addition, the intensity of the shock wave of the D-Opt airfoil was ultimately higher than that of the R-Opt airfoil.

The variation in the drag of the R-Opt airfoil was smaller than that of the D-Opt airfoil, and the variation in the RAE2822 airfoil was the highest.The lift variation had a smaller influence on the lift-to-drag ratio because its amplitude of variation from minimum to maximum was less than 20%while that of drag was about 200%. Consequently, the variation in the lift-to-drag ratio of the R-Opt airfoil was the lowest, and thus it was the most robust, followed by the D-Opt airfoil and the RAE2822 airfoil. Curves of the probabilistic density function in Fig. 24(d) also show this.

6.2.2. Case II: RAE2822, Ma ～U(0.704, 0.764)

The second case involved optimizing the RAE2822 with a different disturbance-related assumption. The disturbance was assumed to follow the uniform distribution of U(0.704,0.764) (i.e., a distribution with a larger disturbance in nearly the same interval). The optimal target for this case is listed in

Table 4 CFD evaluation of different methods for UQ.

The optimal airfoils of all deterministic optimizations and robust optimizations are compared in Table 6. The results show that the airfoil with w=0.5 yielded the most robust performance. This airfoil (also marked as the R-Opt airfoil hereinafter in this case) was selected for comparison with the deterministic optimal airfoil.

Distributions of the lift-to-drag ratios of the RAE2822,the D-Opt,and the R-Opt airfoils are compared in Fig.25(a),and variations in their surface pressure are shown in Figs. 25(b)-(d). The variations in surface pressure were similar with those under the assumption of a normal distribution. However, the entire disturbance interval was of interest in this case, and the sample conditions near the two boundaries of the disturbance interval appeared more frequently than in the previous case. Therefore, the uncertainty (specifically, the standard deviation of K) in the airfoils in this case was higher than that in Case Ⅰ.The physical mechanisms in this case were similar with those of Case Ⅰ. The variation in the lift-to-drag ratio of the R-Opt airfoil was the lowest, and it was the most robust airfoil.

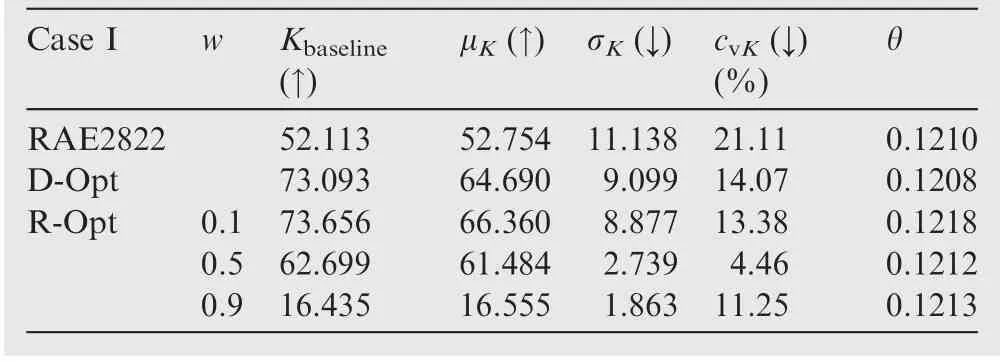
Table 5 Optimal results obtained by using different optimization techniques in Case I.

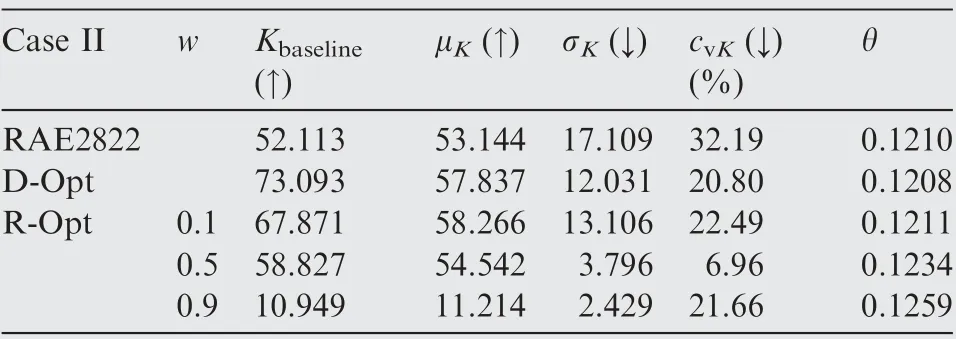
Table 6 Optimal results obtained by using different optimization techniques in Case II.

6.2.3. Comparison between robust solutions of Case I and Case II

Table 7 Uncertainty in airfoils under two disturbance assumptions.

The disturbance intervals in Case I and Case II were similar but the distributions of the disturbances were different. To explore the difference in the solutions, the robust airfoils with w = 0.5 in Cases I and II were compared under the two assumptions of disturbance. Fifty sample conditions were equiprobably selected from each of the disturbance intervals.The airfoils were marked as R-Opt-I and R-Opt-II. The RAE2822 and D-Opt airfoils were also considered.The results are shown in Fig.26 and Table 7.The shaded region in Fig.26 is the violin plot drawn from the distribution of the samples to show the magnitude of the probabilistic density.

It is clear that the distribution of the lift-to-drag ratio of the RAE2822 airfoil was the widest, regardless of the disturbance assumption in Ma.It was the least robust among the four airfoils. That of the D-Opt airfoil was the second widest, and it was the second least-robust airfoil.

For the other two airfoils, when Ma followed the assumption of a normal distribution, the aggregation of values of the lift-to-drag ratio of the R-Opt-I airfoil was greater than that of the R-Opt-II airfoil, and it was more robust. When Ma followed the assumption of a uniform distribution, the ranges of the distributions of the lift-to-drag ratio of these two robust airfoils were similar.However,that of R-Opt-I airfoil clearly inclined to one side,and a number of samples were far from this side.In this case,although the mean value might have been slightly higher, so was the standard deviation.Therefore, it was less robust than the R-Opt-II airfoil under the assumption of a uniform disturbance.

The assumptions of disturbances following a uniform distribution and a normal distribution were completely different,and the forms of distribution of the optimal aerodynamic performance obtained (i.e., the lift-to-drag ratio) via the R-Opt technique were different as well. Nevertheless, they were both more robust than the deterministic optimal result, even under other assumptions of disturbance.Therefore,they can provide a reference for designing the shape of the airfoil in applications under different perturbations.

7. Conclusions

This study proposed and verified an RAO technique called ROpt.It consists of two parts:a procedure for uncertainty quantification and the propagation of the corresponding uncertainty gradient,and a procedure for adjoint solver-based optimization.Following its construction,the R-Opt technique was employed for the optimization of two benchmark functions and two aerodynamic airfoils.The conclusions can be drawn as follows:

(1) The R-Opt technique requires only one process of construction of the PCE model on the target function in each iteration, and the gradient of uncertainty can be inferred via chain rules. It is thus efficient. In addition,it avoids the problem of disagreement regarding the best PCE basis among PCE models (of the target functions,gradient functions, governing equations, and flow variables) encountered in Jameson’s and Kumar’s methods.Moreover,the R-Opt technique supports the application of the sparse PCE method. This will be the focus of our future research.

(2) The R-Opt technique performed well on benchmark tests. It overcame the deficiency of a loss of predictive accuracy near the optimal solution in Kumar’s method.Its predictions were more accurate regardless of the region of the design space or local position near the optimal solution.It performed similarly well to the common statistical approach but was more efficient.

(3) The R-Opt technique can help implement a robust aerodynamic optimization design. The RAE2822 airfoil was robustly optimized by using it under two different assumptions of disturbance. The robust optimal airfoils obtained under one assumption were even superior to the deterministic optimal airfoil when under a different assumption.Therefore,the proposed method can provide a reference for aerodynamic shape design in applications.

(4) The efficiency of optimization of R-Opt is independent of the dimensionality of the design variables. It is constructed based on the adjoint solver, and thus avoids the curse of dimensionality of the design variables. The dimensionality of the design variables of the benchmark tests and the aerodynamic cases varied from 2 to 22,and the R-Opt technique always worked well and efficiently with them.It also supports the independence of the efficiency of optimization and dimensionality.

(5) The maximum dimensionality in disturbance discussed in this research was 3,and the R-Opt technique required 20 samples to quantify uncertainty.If the dimensionality continues to increase, the curse of dimensionality may occur in the process of disturbance quantification. To solve this problem, the authors are working on the sparse PCE, and will add it to the framework of the R-Opt technique in future research.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 11721202).