A gradient-based method assisted by surrogate model for robust optimization of turbomachinery blades

Jiaqi LUO, Zeshuai CHEN, Yao ZHENG

School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310027, China

KEYWORDS Robust aerodynamic design optimization;Turbomachinery;Adjoint method;Surrogate model;Uncertainty quantification

Abstract The design optimization taking into account the impact of uncertainties favors improving the robustness of the design. A Surrogate-Assisted Gradient-Based (SAGB) method for the robust aerodynamic design optimization of turbomachinery blades considering large-scale uncertainty is introduced, verified and validated in the study. The gradient-based method is employed due to its high optimization efficiency and any one surrogate model with sufficient response accuracy can be employed to quantify the nonlinear performance changes. The gradients of objective performance function to the design parameters are calculated first for all the training samples,from which the gradients of cost function can be fast determined. To reveal the high efficiency and high accuracy of SAGB on gradient calculation, the number of flow computations needed is evaluated and compared with three other methods. Through the aerodynamic design optimization of a transonic turbine cascade minimizing total pressure loss at the outlet,the SAGB-based gradients of the base and optimized blades are compared with those obtained by the Monte Carlo-assisted finite difference method. Moreover, the results of both the robust and deterministic aerodynamic design optimizations are presented and compared to demonstrate the practicability of SAGB on improving the aerodynamic robustness of turbomachinery blades.

1. Introduction

By most Aerodynamic Design Optimization(ADO)neglecting the impact of uncertainties,the mean performance may deviate far away from the nominal one and the performance dispersity may be high when the impact of geometric variations,1inlet flow perturbations2are considered. Since this century’s beginning, Robust ADO (RADO) has been studied in aerospace engineering with the impact of manufacturing variability, ice accretion, etc. taken into account.3-6One crucial issue of RADO is Uncertainty Quantification (UQ), by which the mean performance and standard deviation (Std) are statistically calculated. Besides the optimization method used for searching for the optimal,the optimization efficiency and accuracy considerably depends on UQ method. Up to now, the direct Monte Carlo Simulation (MCS),1surrogate model7and sensitivity analysis8have been used in uncertainty studies of turbomachinery.Thus careful studies and selections of optimization method and UQ method are significant for RADO.

In the past decade,a few of studies on RADO of turbomachinery were reported, Keane9studied different compounded methods, finding that the method with MCS-based UQ is the most time-consuming but the most accurate. Ghisu et al.10introduced a procedure for RADO of multi-stage compressors with performance impact evaluating by polynomial chaos.The performance parameters were fast calculated by a onedimensional analysis program, thus the UQ and optimization methods have little impact on the optimization efficiency.Kamenik et al.11, Gao et al.12introduced a RADO method for the design optimization of turbomachinery blades considering geometric variability, in which the nonintrusive UQ method and Kriging model were employed. Luo et al.13studied the gradient-based design optimization of a turbine blade considering geometric variability, in which Second-Order Sensitivities (SOS) were used for performance impact evaluation.Generally, the methods used in the aforementioned work9-13can be categorized by three types, ‘‘MCS-based” with the direct MCS-based UQ, ‘‘model-model” with model-based UQ and model-based optimization, and ‘‘sensitivity-sensitivit y” with SOS-based UQ and FD-based gradient calculation.

Among the three types RADO methods, the latter two are more efficient than the MCS-based one. However, for the design optimization with a large number of design parameters,model-based optimization is time-consuming and sometimes low-fidelity. Moreover, sensitivity-based UQ is inaccurate when the performance changes are strong nonlinear dependent on the uncertainty, which is named large-scale uncertainty in the present study in order to differ from the small-scale uncertainty, i.e., the performance changes can be accurately evaluated by the sensitivities. In the present study, a sensitivitybased RADO method,which can be assisted by any one surrogate model is introduced to accurately and efficiently evaluate the performance impact and efficiently accomplish the design optimization. The principles of this Surrogate-Assisted Gradient-Based(SAGB)optimization method are firstly introduced in detail.Then the RADO optimization method is carefully verified and validated. Finally, it is applied to the design optimization of a transonic turbine cascade. The results are presented and compared.

2. RADO methods

2.1. UQ methods

The principles and implementations of SAGB are introduced in this section. UQ is the most time-consuming module in RADO,thus the sensitivity-based and model-based UQ methods are introduced briefly.

Using the First-Order Sensitivities (FOS) and SOS, performance can be fast evaluated by

where the first and second order derivatives are the corresponding FOS and SOS, f0, f and uiare the deterministic,stochastic performance functions and uncertainties, respectively, m is the number of uncertainties. By using a ‘‘directadjoint” method, only m+2 flow computations are necessary to determine all the sensitivities.8

Using surrogate model methods, the Response Surface Model (RSM) is firstly constructed with the given training samples. By solving a group of linear equations HB = F,

where H and F are the kernel matrix and the output vector,respectively, the coefficient vector B can be obtained. Then the RSM can be used for function response.

where Hiand biare the ith kernel function and the corresponding coefficient, u and h(u) indicate the input and the corresponding kernel vector. The efficiency of model construction depends on the number of training samples, which inherently depends on the number of uncertainties.

To evaluate the performance of different UQ methods, a transonic turbine cascade, HS1A, is studied. Fig. 1 is the configuration.14The inlet total pressure and total temperature are 101325 Pa and 288.15 K, respectively. The outlet isentropic Mach number is 1.04. The design inlet flow angle, α is 46°,the maximum variation of which, δα is 5° in the study. The impact of inlet flow angle variations on total pressure loss will be studied.

where p0is the total pressure and the subscripts 1, 2 are the inlet and outlet, respectively.

The total pressure loss with varying inlet flow angle is calculated by both SOS and a cubic polynomial RSM constructed by eleven training samples. Fig. 2 compares the total pressure loss variations, where CFD are the ones of test samples,while samples are the ones of training samples for model construction. Eleven samples are adaptively produced using the leave-one-out cross validation method.15It is clear that the RSM-based results agree well with the CFD ones in the whole uncertainty space. Although only three flow computations are required by SOS analysis, the predicted total pressure loss deviates far away from the CFD ones in most of the space. In other words, the sensitivity-based UQ methods are accurate only for small-scale uncertainties,i.e.,the inlet flow angle variation not exceeds 3°.One of the main purposes of UQ is accurately calculating the statistical mean performance and Std for RADO. When the maximum inlet flow angle variation is 5°,model-based UQ method is employed to develop the SAGB method.

2.2. Principles of SAGB

With the given probability density function of uncertainties, a large number of statistic samples can be randomly produced and the objective performance function can be calculated by Eq. (2). Then the statistical mean μ and variance σ2are

where N0is the number of statistic samples,uiis the ith sample.Following the same procedure, the statistics (mean, variance,Std,etc.)of each modified blade resulted from design parameter perturbation can be calculated. The gradients of statistical mean and Std to the design parameter xiare

where μ0and σ0are the statistics of the base blade.The gradients are calculated by Finite Difference (FD). By such a RADO method, UQ and FD are accomplished in sequence.This method is named SAGB-I in the study.

By SAGB-I, the methods of UQ and gradient calculation are employed step by step.Since the number of flow computations for obtaining the gradients by FD is linearly dependent on the number of design parameters N, this method is timeconsuming if N is large. A deep compounded SAGB method is in need of study.

With the given training samples,the surrogate model can be constructed by solving the matrix equations F=HB.With the same training samples, surrogate models of the gradients of objective performance function to the design parameters can also be constructed.

where n is the number of training samples,Bg,iis the coefficient vector of the ith gradient surrogate model.Mentioned that Bg,iis only the nominal first variation of B,not the exact one.It is determined by solving the linear equations,Eq.(7).Ultimately,N+1 surrogate models require to be constructed,one for the objective performance function and the others for the gradients.

From Eq. (4) and Eq. (7), the gradients of statistical mean and Std to the design parameters are

It is known from Eq.(8)that once all the coefficients of surrogate models are determined by solving N+1 groups of linear equations, the gradients of statistics can be fast calculated without any more flow computations, supposing that the gradients of objective performance function to the design parameters for all the training samples have already been given.This method is named SAGB-II in the following study.

Not only the mean performance but also the robustness requires to be improved by RADO.Thus RADO is one typical multi-objective optimization problem. By using the gradientbased optimization method,the cost function is usually defined in the following weighted summation form.

The implementation procedures of SAGB-II are summarized as follows.

Step 1.Generating a series of training samples by design of experiment in the uncertainty space and then calculating the performance function. Adaptive sampling methods can be used to accelerate model construction.

Step 2. Calculating the gradients of objective performance function to the design parameters for all the training samples by some high efficiency and high accuracy sensitivity calculator, such as the adjoint method.16

Step 3. Constructing the surrogate models and evaluating the function response performance. Additional samples are necessary if the function response error exceeds the tolerance and return to Step 2.

Step 4. Generating a large number of statistic samples and then calculating the gradients of statistical mean and Std to the design parameters following Eq. (8).

Step 5. Applying the method to RADO once the accuracy of gradients is validated.

The continuous adjoint method,pioneerly applied to ADO by Jameson16,has been widely used in the design optimization of turbomachinery.17-22By this method, the complete FOS of each objective performance function can be obtained with the computational cost of two equivalent flow computations. The authors have calculated the FOS by the adjoint method,which were then applied to the design optimization of turbomachinery.18,20Herein the adjoint method is not introduced in the study. In the following, the efficiency and accuracy of SAGB-II will be verified and validated by comparing with other methods.

3. Results and discussion

3.1. Verification and validation

In this section, the optimization efficiency of four different methods and the accuracy of gradients of SAGB-II are carefully verified and validated.

Table 1 gives the total numbers of flow computations ntof four RADO methods.In the table,RSM and SOS indicate the methods of ‘‘model-model” and ‘‘sensitivity-sensitivity”,respectively, as introduced before. For ease of comparison,the simple quadratic polynomial RSM is taken as the example and

where n1and n2are the estimations of training sample numbers for RSM with N and m inputs, respectively. It is known that the training samples are usually several times as much as the kernel functions. a is a growth factor, which reaches up to a large value to achieve the desired response accuracy. Moreover, for the latter three gradient-based optimization methods as shown in Table 1, ntis the number of flow computations in each design cycle. Mentioned that for SOS, m + 2 equivalent flow computations are necessary for SOS calculations by the‘‘direct-adjoint” method8and the procedures repeat N + 1 times when FD is employed to calculate the gradients.

Fig.3 gives the contours of the ratio of flow Rfcomputation number for the former three RADO methods to that of SAGB-II as shown in Table 1.

where n0denotes the total number of flow computations,which is the product of ntand the maximum design cycle for the gradient-based methods. To plot the contours, a medium growth factor a = 4 is given and a medium maximum design cycle,thirty is given for the gradient-based optimization methods.It should be pointed out that the maximum design cycle of gradient-based optimization depends on the optimization method, such as the simple steepest descent method, quasi-Newton method,etc.Thirty is a moderate value,which is only used for the estimations of Rf.

From Fig. 3 it can be found that

(1) The ratio,Rfis independent on the number of uncertainties for RSM and SAGB-I, while it increases fast as N increases.The optimization efficiency of these two methods is comparable with SAGB-II only when the design parameter number is very small.

(2) The variations of Rffor SOS are interesting. The total number of flow computations of SOS is less than or more or less equal to that of SAGB-II only in such cases that either m is large or N is very small.That’s because if m is large, SOS-based UQ is more efficient than the model-based UQ of SAGB-II.

Take the RADO of the transonic turbine cascade for example,the design parameter number is six and only the inlet flow angle variation is considered. Cubic polynomials are used as the kernel functions. Under the condition that n2= 11 as shown in Fig. 2 and suppose the gradient-based optimization can be accomplished in thirty design cycles, the ratio Rffor the three former RADO methods are 1.71, 0.95, 3.50, respectively. Although the optimization efficiency of SOS is close to that of SAGB-II, but it is the most difficult to achieve among the four because high-order sensitivities should be calculated. Furthermore, SOS-based UQ is accurate only for the small-scale uncertainties.

The turbine cascade is optimized by imposing six uniformly distributed Hicks-Henne shape functions23on the base camber.

where δc, bs,i, Vi, xc,iindicate the variation of camber, shape functions,weights to be optimized,control points of the shape functions, respectively.

To verify the accuracy of gradients calculated by SAGB-II,MCS-based UQ is also employed to calculate the gradients.Considering the computational cost,only 200 statistic samples uniformly distributed in the space [-5°, 5°] are used. The gradients of statistical mean and Std are calculated following Eq.(5). With the cost of 1400 flow computations, the complete MCS-based gradients are determined and presented in Fig. 4. It is clear that the gradients obtained by SAGB-II are almost duplicates of those of MCS, with the cost of only 22 equivalent flow computations.To further validate the accuracy of the gradients by SAGB-II, the gradients of the statistics for the RADO optimized blade are also calculated and comparedin Fig. 4, demonstrating excellent agreements with the MCS ones again. It should be emphasized that UQ based on only 200 statistic samples quite probably reduces the gradients’accuracy,but it can still be used for the comparison-based verification and validation of the new method.

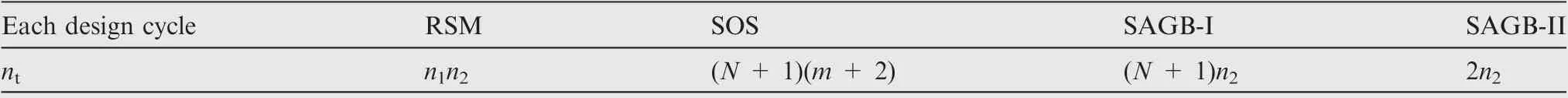
Table 1 Number of flow computations.

3.2. Application of SAGB-II

The method SAGB-II will be further validated in this section through application to aerodynamic design optimization.The cost function of RADO is given by Eq. (9) with λ = 0.5. Only one optimization, rather than the multiobjective optimization with a series of different weights is presented to investigate the practicability of the robust optimization method. To reveal the effectiveness of RADO on improving the robustness, a Deterministic ADO (DADO) is also carried out in the study with the cost function defined by Eq. (3). The same parametrization method is employed.The steepest descent method is used.

The optimization results are listed in Table 2. DADO and RADO are sufficiently converged in thirty design cycles. By using the cubic polynomial-based surrogate model, performance impact for the base and DADO blades are evaluated using 200,000 uniformly distributed statistic samples in [-5°,5°]. The statistics and their variations of the base blade,DADO and RADO blades are given in the table. It can be found that both DADO and RADO can reduce the mean total pressure loss and Std, but more gains on statistics’ reductions can be obtained by RADO.

The optimization is performed at the design inlet flow angle. The statistical performance at the off-design conditions are evaluated in the study. Fig. 5 presents the statistical mean total pressure loss with the inlet flow angle varying from 36°to 56°. At the design condition circled in red, the deviation of total pressure loss of RADO is far less than the other two.Moreover, the total pressure losses of RADO are the lowest in the whole range, showing the effectiveness of RADO on improving the mean performance,even at the off-design conditions.Furthermore,as the inlet flow angle increases,the statistical means increase faster than the ones neglecting uncertainties, demonstrating that the impact of uncertainty is stronger at high inlet flow angle. Suppose that the transonicturbine cascade is optimized at high inlet flow angles, more gains on statistics’ reductions can be obtained.

Table 2 Statistics of total pressure loss for different blades.

Fig. 6 compares the profiles of the base, DADO and RADO blades. To better illustrate the profile changes, the blade profiles near the Leading Edge (LE) are enlarged.Fig.7 compares the isentropic Mach number Ma distributions on the blade. It can be found that the optimized cambers are less curved around LE,which is responsible for the flow deceleration on the suction side of the optimized blades,as shown in Fig.7(a).Moreover,as shown by the red circle in Fig.7(a),the shock wave on the suction side from 60% to 80% axial chord of the base blade moves downward after optimization, resulting in mean performance improvements of the optimized blades.

To demonstrate the effects of design optimization on robust improvements, the flow solutions of 200 random samples agreeing the uniform distribution in [-5°, 5°] are calculated for the base, DADO and RADO blades. The statistical mean and Std distributions of isentropic Mach number change are subsequently calculated and given in Fig. 7(b) and (c). It can be found that the statistical mean and Std on most of the suction side are significantly reduced after optimization. More reductions of statistics are obtained by RADO.

It is known that the aerodynamic robustness depends on the flow sensitive to uncertainties. As shown by Fig. 7(a), the maximum isentropic Mach number near LE of the base blade is close to one at the design condition.With positive changes of inlet flow angle, the flow near LE accelerates, resulting in increased mean isentropic Mach number and increased mean shock loss. After optimization, the less curved camber favors flow deceleration near LE. That is why the statistical mean Mach number near the suction peak is significantly reduced for DADO and RADO blades.Moreover,the reduced suction peak is responsible for the reductions of statistical mean and Std on most of the suction side of the optimized blades. The downstream movement of shock wave on the suction side is responsible for the flow loss reduction. However, the flow around shock wave is still sensitive to the variations of inlet flow angle for the optimized blades. As shown by Fig. 7(b)and (c), the maximum statistical mean and Std of the optimized blades are close to those of the base blade.The positions of the maximums correspond with those of the shock waves.On the portions from 60% to 70% axial chord, the statistics of the optimized blades decrease due to the downstream moved shock wave.However,on the portions from 70%to 90%axial chord, the statistics of the optimized blades are even higher than those of the base blade. Compared with the shock wave,the reduced suction peak contributes more to the robust improvements.

4. Conclusions

(1) Be different from the ‘‘model-model” and ‘‘sensitivity-s ensitivity” methods, a deep compounded gradientbased optimization method, which can be assisted by any one surrogate model is implemented in the study with the purpose of improving optimization efficiency and accuracy simultaneously for the aerodynamic dynamic optimization of turbomachinery blades with large-scale uncertainty.

(2) The optimization efficiency of SAGB-II is verified and validated to be higher than other RADO methods in most instances. Moreover, the gradients of statistics by SAGB-II are also verified and validated by comparing with those obtained by MCS, finding that the SAGBII-based gradients are almost duplicates of MCS-based ones. The excellent performance of SAGB-II on optimization efficiency and accuracy are clearly illustrated through RADO considering large-scale uncertainties.However, when quite a few of small-scale uncertainties are taken into account, the optimization method with SOS-based UQ probably performs better.

(3) SAGB-II is applied to the design optimization of a transonic turbine cascade reducing the mean and Std of total pressure loss. The results are compared with the base blade and those obtained by DADO.Through the aerodynamic optimization weakening the shock wave in inviscid flow, the aerodynamic robustness can be improved. Compared with DADO, more gains on the reductions of statistical mean and Std can be obtained by RADO, demonstrating that SAGB-II is practicable for robust design optimization of turbomachinery blades.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationship that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by National Natural Science Foundation of China (Nos.51676003, 51976183) and National Science and Technology Major Project of China (No. J2019-II-0012-0032).