基于PCA-VMD-CNN的输电线路覆冰重量预测模型*

李 波，李 鹏，高 莲，杨家全，包慧琪

(1.云南大学 信息学院，云南 昆明 650500；2.云南省高校物联网技术及应用重点实验室，云南 昆明 650500；3.云南省电网有限责任公司，云南 昆明 650217；4.云南大学 软件学院，云南 昆明 650500)

0 引言

覆冰作为1种自然现象，给世界各地输电线路造成严重破坏，其可以引起导线舞动、金具破坏、跳闸停电、电杆倒、导线折断等事故。因覆冰负荷超限造成高压输电线路倒(杆)、线路拉断等事故时有发生[1-3]。

目前国内外已开展大量研究工作并取得了较大进展。文献[3]从空气动力学和热力学角度出发提出最优时间步长模型，然而需要大量微观参数才能保证预测精度；文献[4-5]基于传统时间序列分析的方法构建预测模型，模型对处理平稳的覆冰过程效果尚可，但对非平稳状态下的覆冰过程预测效果欠佳，抗干扰能力差；文献[6-10]基于影响覆冰负荷的气象因素建立机器学习回归模型，然而气象数据的采集误差较大[11]，只用气象数据建立的回归模型预测精度有限。

因此，本文建立1种基于PCA-VMD-CNN的输电线路覆冰短期的预测模型。首先对气象因素进行主成分分析(Principal Component Analysis,PCA)，降低数据维度，然后对覆冰历史重量进行变分模态分解(Variational Modal Decomposition,VMD)，将原始覆冰重量分解为不同变化趋势的分量[12-13]，并根据每个分量建立卷积神经网络(Convolutional Neural Network， CNN)模型分别进行预测，再将各分量分别预测的结果叠加组合得到预测的最终值。本文模型既考虑影响导线覆冰重量的气象因素，又考虑历史覆冰的影响以及覆冰过程的非平稳态，以期为电力系统的安全可靠运行提供更可靠的覆冰预警。

1 基本原理

1.1 主成分分析

主成分分析是处理高维数据的1种统计学习方法，对数据矩阵的协方差矩阵进行特征值分解，达到降维的目的。PCA主要分为4个步骤。

原始数据矩阵如式(1)所示：

(1)

式中：n为数据个数；p为特征数。

1)数据标准化(中心化)的矩阵X*表示如式(2)：

(2)

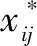
2)计算标准化后的协方差矩阵R，如式(3)所示：

(3)

3)求R的特征值和特征向量。

4)计算主成分贡献率及累计贡献率。贡献率计算如式(4)，累计贡献率计算如式(5)所示：

(4)

(5)

选取累积方差贡献率在75%～95% 时，对应的前q个主成分包含原始p个变量所能提供的绝大部分信息。

1.2 变分模态分解

变分模态分解算法(VMD)由Dragomiretskiy提出，是1种自适应而且通过迭代搜索的信号分解技术。VMD可以将原始信号f(t)分解为具有不同中心频率和带宽的子信号，每1个子信号都是原始数据的1个本征模态函数(IMF)。每1个IMF表示原始信号在不同尺度下的变化趋势。对于信号f(t)的约束变分模型如式(6)所示：

(6)

式中：uk为第k个IMF分量；wk为第k个IMF分量的中心频率；dt为函数时间导数；δ(t)为单位冲激函数；j为虚数单位；t为时间变量；⊗为卷积运算。

引入惩罚因子α和拉格朗日惩罚算子λ，约束变分问题就转为非约束性变分问题，如式(7)所示：

(7)

VMD求解过程如下：

2)采用乘子交替算法更新{uk},{wk},λ。

3)给定精度ε，若满足精度则停止更新，如式(8)所示；否则继续更新。

(8)

1.3 卷积神经网络

卷积神经网络(CNN)是1种前馈网络，由卷积层、池化层、全连接层和输出层组成，图1为CNN结构模型。

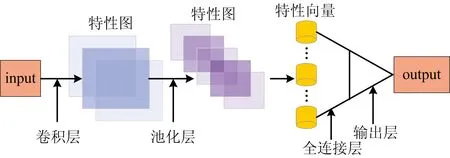
图1 卷积神经网络模型Fig.1 Model of convolutional neural network

卷积层是CNN的核心，在卷积层上，卷积核通过设定的移动步长完成对各输入特征图的卷积滤波，提取局部特征，输出特征图。运算公式如式(9)所示：

Y=Relu(W⊗X+B)

(9)

式中：X为输入特征；W为卷积核；⊗为卷积运算；B为偏置；Relu为激活函数:Relu(x)=max(0,x)。

卷积运算过后对特征图进行池化操作，在一定范围取最大值或平均值，池化可以减少模型参数，防止过拟合。

在全连接层上,把从输入点展开的一维特征矢量经过加权求和，使用激活函数计算得到，如式(10)所示：

yk=Rule(ωkxk-1+bk)

(10)

式中：yk为输出；k为第k层全连接层；ωk为连接权重；xk-1为展开的一维图；bk为偏置。

CNN采用梯度下降法来更新ω，b使损失函数达到最小，损失函数选择均方差损失函数如式(11)所示：

(11)

式中：N为样本数量；y为样本标签；Relu(ωx+b)为通过全连接层的输出值。

2 输电线路覆冰重量预测模型

本文预测模型的基本思想是通过覆冰历史重量及当下气象数据来预测覆冰数据，可分为以下5个部分：

1)数据预处理。

2)气象数据主成分分析。

3)将历史数据通过VMD分解为多个IMF分量。

4)将气象数据和历史覆冰重量各个IMF组合为新的输入矩阵。

5)将输入矩阵输入到CNN模型，将每个分量的预测结果相加。

具体流程如图2所示。

图2 VMD-CNN覆冰预测流程Fig.2 Flow chart of ice coating prediction by VMD-CNN

2.1 数据预处理

为降低异常数据对预测的干扰以及避免不同特征之间数值差距太大，提高收敛速度，本文对数据进行以下处理。首先，输电线路结冰的基本条件是温度<0 ℃，相对湿度>80%等，根据此依据剔除异常数据[8]；其次，进行数据归一化。

本文将数据归一化到(0,1)之间，如式(12)所示:

(12)

式中：yg为归一化后得到的数据；y为归一化的原始数据；ymax为原始数据的最大值；ymin为原始数据的最小值。

2.2 构造输入矩阵

设提取的主成分为W=[w1,w2,…,wq]，q为提取的主成分个数。设输入的N个历史覆冰重量T=[t1,t2,…,tn]。将前n个历史数据和第n+1时刻的气象数据构造为输入矩阵预测第n+1时刻的覆冰重量。输入矩阵如式(13)所示：

(13)

由于卷积神经网络的优点在输入图像时表现的更为明显，因此将输入构造为二维矩阵输入到卷积神经网络里进行训练和预测，经实验证明，构造为二维矩阵可以提高预测精度。

2.3 多步长预测

多步长预测是建立在15 min的单步预测基础上，假设天气因素不变，将前一步长预测中得到的覆冰重量预测值作为实际值代入，图3为多步长预测流程。

图3 多步长预测流程Fig.3 Flow chart of multiple step size prediction

2.4 评价指标

本文采用均方根误差RMSE、平均绝对误差MAE和决定系数R2对模型进行评价。RMSE和MAE越小越好，R2表示模型的拟合效果，越接近于1，拟合效果越好[14]。

均方根误差(RMSE)计算如式(14)所示：

(14)

平均绝对误差(MAE)计算如式(15)所示：

(15)

决定系数(R2)计算如式(16)所示：

(16)

3 实例分析

3.1 数据来源

为验证模型的有效性和可行性，本文选取某电网公司输电线路在线监测系统采集的覆冰过程中数据进行模型验证，如图4所示。本文数据采样间隔时间均为15 min， 图4～6、图8～9横坐标数字表示采样次数，即第x个15 min。

3.2 光照强度处理

由于光照强度的特殊性(夜晚会骤降到0)，直接代入模型会影响光照和覆冰之间的相关性，因此对光照强度应取1天的平均值来代替原始值。图5为光照强度处理前后对比结果。

图4 覆冰过程Fig.4 Process of ice coating

3.3 主成分提取

将6个气象因素进行主成分分析。得到6个变量的协方差矩阵以及主成分累计贡献率如表1所示。

图5 光照强度处理结果Fig.5 Processing results of light intensity

表1 6个变量协方差特征值Table 1 Covariance eigenvalues of six variables

由表1可知，前4个主成分的贡献率达到94%，可以解释原始数据绝大部分信息，因此提取前4个主成分作为模型输入。

3.4 VMD分解

将历史覆冰数重量分解为6个IMF分量，图6为原始数据与分解结果。

图6 原始数据与VMD分解结果Fig.6 Original data and results of VMD decomposition

3.5 卷积神经网络参数的设置

如上文所述，本文利用前n个历史覆冰重量和第n+1时刻的气象数据作为模型输入，第n+1时刻的覆冰重量作为期望值与模型预测值进行误差比较。为寻找最佳n的值，采用均方根误差作为评价指标，即RMSE越小，训练效果越好。图7为不同n值下的训练集的RMSE的大小。由图7可以看出，当n为6时，训练集均方根误差最小。

图7 不同n值下训练集的RMSEFig.7 RMSE of training sets under different n values

卷积神经网络的输入为十维(前6个时刻的覆冰重量加上4个主成分)，通过式(13)构造为10×10输入矩阵。因此，输入层大小为10×10，卷积核大小选为3×3×16(16为卷积核层数)，池化层大小为2×2，通过简单计算，输入通过卷积层化之后的大小为4×4×16，展开为256×1的向量输入到全连接层，全连接层的隐藏层神经元第1层选取16个，第2层选取4个，输出层神经元个数为1。

3.6 预测结果对比

为分析本文模型的优势，选取LSTM(长短期记忆人工神经网络)，LSSVM(最小二乘支持向量机)[8，15]，WNN(小波神经网络)[6]，CNN与本文模型进行对比。由图4可知，数据的第2 022到2 162之间覆冰最严重，所以本文选取1到2021个数据为训练集，2 022到2 162个数据为测试集进行单步和多步预测。

单步长预测结果如图8所示。表2为6种模型单步长评价指标对比。表3～5分别为6种模型的多步长预测评价指标对比结果，图9为模型单步长绝对值误差对比结果。

由图8可知，当预测步长为1时，6种模型的预测曲线与实际值基本一致，基本可以反映实际覆冰重量。由表2可以看出，本文模型明显降低了误差，提高预测精度，对比图9的误差曲线不难看出，WNN,LSSVM,LSTM模型的前85个测试样本绝对值误差在100 kg上下浮动，CNN在50 kg左右浮动，而本文模型仅在20 kg上下浮动。测试集数据中，WNN,LSSVM,LSTM,CNN 4种模型最大绝对值误差均超过200 kg，本文模型(二维)绝对值误差仅为46 kg；并且，在对覆冰最大值进行预测时，其他4种模型绝对值误差均超过30 kg，本文模型仅为6 kg。

图8 模型单步长预测结果对比Fig.8 Comparison on prediction results of different methods

表2 单步长结果对比Table 2 Comparison of single step size results

表3 多步长预测值RMSE对比Table 3 Comparison of multiple step size prediction value RMSE

表4 多步长预测值MAE对比Table 4 Comparison of multi step predicted value MAE

表5 多步长预测值R2对比 Table 5 Comparison of multiple step size prediction value R2

图9 模型单步长绝对值误差对比Fig.9 Comparison on absolute value error of single step size in model

当K=2,4时，对比表3～5，本文模型具有明显优势。然而当K=8,16时，本文模型(一维)并没有什么优势，由此利用卷积神经网络的优势，将一维数据构造为二维矩阵，对单步长预测和多步长预测精度有明显的提升。可以看出，在大多数情况，本文预测模型优于其他模型，从而证明本文模型的可行性和优越性。

4 结论

1)架空输电线路覆冰负荷与地理环境、宏观气象因子之间存在非常复杂的多层依赖关系，单纯依靠气象信息误差大、精度低。本文将气象数据与历史覆冰相结合建立预测模型，通过实验证明，本文所构建的预测模型安全性更高、可靠性更强，对单步长和多步长、平稳态和非平稳态覆冰过程都有着很好的预测效果，具有重要工程实践意义。

2)架空输电线路覆冰时间序列具有多尺度特性、非平稳性。如果对原始序列直接预测精度低，通过VMD将非平稳的随机线路覆冰负荷序列数据自适应分解为若干个具有不同尺度特征的IMF分量，对每个分量分别预测，通过实验分析，VMD分解能够有效提高预测精度。

3)深度学习网络具有浅层神经网络没有的优势，可以更好地表示复杂的函数，而卷积神经网络对二维数据的特征提取能力很强，因此本文利用这一特性将历史覆冰数据重构为二维数据，进一步提高预测，然而深度学习参数的选择只能通过经验选择，可解释性差，未来可进一步开展研究。