基于响应曲面法的有效抽采半径多因素交互影响机制研究*

韩飞林，薛 生，郑春山，江丙友，龚选平，韩柏青

(1.安徽理工大学 安全科学与工程学院，安徽 淮南 232001；2.合肥综合性国家科学中心能源研究院(安徽省能源实验室)，安徽 合肥 230031；3.中煤能源研究院有限责任公司，陕西 西安 710054；4.中煤新集能源股份有限公司，安徽 淮南 232001)

0 引言

随着我国煤炭开采逐步走向深部，瓦斯赋存条件变得更加复杂[1]，瓦斯事故频发，严重威胁煤矿工人的生命安全。为保障煤矿井下的安全高效开采，我国十分注重煤层瓦斯治理，主要通过施工钻孔抽采煤层中的瓦斯，待瓦斯抽采达到安全标准后，再对煤层进行安全开采[2-3]。钻孔有效抽采半径反映钻孔周围的抽采达标范围[4]，是钻孔设计和施工的基础依据，故该参数是钻孔瓦斯抽采技术非常重要的参数之一。影响钻孔有效抽采半径的因素有很多，例如煤层初始渗透率、原始瓦斯压力、抽采时间以及抽采负压等[5]。

国内外学者在这方面开展了一些卓有成效的研究：郝富昌等[6]建立了蠕变-渗流耦合作用下的瓦斯运移模型，分析不同埋深时钻孔孔径变化规律，及其对有效抽采半径的影响；张翔等[7]以中马村矿为研究背景，运用现场试验和数值模拟相结合的研究方法，研究了不同冲煤量对有效抽采半径的影响规律；Fang等[8]分析了瓦斯抽采过程中多场多相的耦合机理，模拟研究了不同因素对瓦斯抽采效果及有效抽采半径的影响；Wu等[9]以常村矿3号煤层为研究对象，提出1种基于FLAC3D的瓦斯抽采半径确定方法，并采用压降指数法对计算结果进行了验证；邹士超等[10]建立钻孔周围单元体瓦斯渗流模型，模拟得到不同抽采时间下钻孔径向瓦斯压力分布图及有效抽采半径，并与现场试验结果相互验证；张天军等[11]使用相似模拟试验和数值模拟2种方法，分析负压变化对煤体瓦斯渗流特性的影响；Kong等[12]建立了流-固耦合渗流模型，研究了水力冲孔后不同因素对有效影响半径的耦合影响；Qin等[13]基于钻孔周围煤体的垂直应力-渗透函数关系，建立了钻孔周围煤体瓦斯渗流的数值计算模型，并分析了抽采时间、初始瓦斯压力、钻孔孔径和抽采负压对钻孔有效抽采半径的影响。

目前聚焦于单一因素对钻孔有效抽采半径影响的研究较为普遍，这与有效抽采半径同时受到多种因素交互作用的现实状况不符。为了准确有效地分析有效抽采半径对各因素的敏感性，确定有效抽采半径与多因素之间的关系，得到各因素的影响显著性高低，本文基于响应曲面试验设计及数据模型分析，运用COMSOL Multiphysics软件研究不同抽采条件下的钻孔有效抽采半径变化规律，分析单因素及多因素交互作用对有效抽采半径的影响机制，以及各个因素的主次关系，建立钻孔有效抽采半径与多因素之间的响应曲面模型，拟为类似矿井有效抽采半径优化提供一定的参考，保障煤矿安全高效开采。

1 理论模型与数值模型

1.1 流动方程

煤层中的瓦斯在流动过程中的质量守恒方程[14]如式(1)所示：

(1)

式中：Qs为瓦斯质量源汇项，kg/(m3·s)；ρg为瓦斯密度，kg/m3；qg为瓦斯达西速度矢量，m/s；m为煤体中游离瓦斯和吸附瓦斯含量，kg/m3；t为时间，s。

单位体积煤基质中存储的瓦斯总量如式(2)所示：

(2)

式中：Φ为煤层孔隙率，%；ρga为标准状态下的瓦斯密度，kg/m3；ρc为煤体密度，kg/m3；VL为体积常数，m3/kg；p为孔隙压力，MPa；PL为朗缪尔压力常数，MPa。

由于瓦斯密度与孔隙压力成正比。根据理想气体定律，瓦斯密度如式(3)所示：

(3)

式中：Mg为瓦斯分子质量，kg/mol；Z为气体非理想状态的修正因子；R为通用气体常数，J/(mol·K)；T为温度，K。

根据达西定律，流速与压力梯度成正比，如式(4)所示：

(4)

式中：μ为瓦斯动力黏度，Pa·s；k为渗透率，m2。

将式(2)～(4)代入(1)中，可得瓦斯在煤层中的流动方程[15]，如式(5)所示：

(5)

式中：pa为标准大气压，MPa。

1.2 渗透率模型

渗透率是影响瓦斯流动的关键因素，因为煤具有典型的双重孔隙结构，煤的渗透率很大程度上取决于煤体割理，在采动影响下煤体割理发生显著变化。假设将割理间距设为常数，渗透率变化可用孔隙度变化的立方函数[16-17]来表示，如式(6)所示：

(6)

式中：k0为初始渗透率，m2；Φ0为煤层初始孔隙率，%。

1个方向上孔隙度的变化受到另外2个方向上由应力变化和瓦斯吸附解吸所引起的总等效应变影响，如式(7)所示：

(7)

式中：i，j=x，y，z对应三维模型的3个方向；ki为i方向上的渗透率，m2；ki0为i方向上的初始渗透率，m2；Δεej表示在j方向上的总等效应变变化量。

总等效应变变化量如式(8)所示：

(8)

式中：Δεsj为应力变化在j方向引起的应变变化，Δεgj为瓦斯吸附解吸在j方向上引起的线性应变变化。

且Δεsj，Δεgj分别如式(9)～(10)所示：

Δεsj=εj-εj0

(9)

(10)

式中：εj，εj0分别为煤在j方向上的应变和初始应变；εL为朗缪尔体积应变常数；p0为初始孔隙压力，MPa。

联立式(7)～(10)可得式(11)：

(11)

本文将使用COMSOL软件解算如上模型，获得不同参数条件下钻孔的有效抽采半径，分析不同因素对有效抽采半径的影响，并通过响应曲面法着重分析多因素交互作用对有效抽采半径的影响。

1.3 数值模型建立

首先建立三维几何模型，模型沿走向上的总长度为130 m，沿倾向上的总宽度为200 m，模型高度即煤层的厚度为5 m，在煤层中共布置10个顺层抽采钻孔，每个钻孔之间的距离为10 m，依据现场施工参数，钻孔孔径为94 mm，钻孔的总长度为174 m，钻孔封孔段的长度为15 m。

模型四周设置辊支承边界，即在x和y方向上位移为零，模型底部设置固定约束边界，模型整体可以发生沉降。模型上表面施加均布载荷压应力，压应力值依据公式σZ=γh计算得出，σZ=18 MPa(γ为上覆岩层平均容重；h为埋深)。网格划分采用物理场控制网格进行划分，网格包含707 482个域单元，57 744个边界单元和14 754个边单元，其他区域的网格划分相对稀疏，钻孔周围的网格划分密集。煤体孔隙度为0.01，瓦斯密度为0.716 kg/m3，瓦斯动力黏度为1.8×10-5Pa·s，巷道压力边界为大气压值0.101 3 MPa，抽采负压为23 kPa。模型示意图如图1所示，抽采钻孔网格划分图如图2所示。

图1 模型示意Fig.1 Schematic diagram of model

图2 抽采钻孔网格划分Fig.2 Grid division of drainage boreholes

2 结果分析与讨论

2.1 单一因素作用对钻孔有效抽采半径的影响

由于在三维模型中无法清楚地观察瓦斯压力的分布情况，因此取三维模型中的二维截面，分析二维截面上的瓦斯压力分布，如图3所示。图4为煤层初始渗透率0.505 mD、原始瓦斯压力1.2 MPa条件下钻孔抽采180 d时二维截面上的瓦斯压力分布图。可以看出，离钻孔越近的区域瓦斯压力下降程度越大，与钻孔距离越远的区域，瓦斯压力变化越小。钻孔封孔段区域被水泥封堵，因此封孔段周围的瓦斯压力无变化。靠近巷帮一侧的煤体瓦斯压力也发生变化，这是因为此处煤壁中的瓦斯压力与巷道中的大气压也存在压差，煤壁中的瓦斯沿着裂隙不断涌出。此模拟结果与张学博等[18]、周西华等[19]的研究结果相比，瓦斯压力变化区域和降低趋势等基本吻合，证明了数值模型的正确性，模型可以用于后续响应面分析研究。

图3 二维截面Fig.3 Two-dimensional section diagram

图4 钻孔抽采180 d后瓦斯压力分布Fig.4 Distribution of gas pressure after 180 days of borehole drainage

煤层渗透率一直是影响瓦斯抽采的重要因素之一，煤层渗透率越大，表明煤体裂隙发育越好，为瓦斯流动提供了良好的通道，瓦斯抽采效果也越好。根据《煤与瓦斯突出危险性区域预测方法》(GB/T 25216—2010)[20]，判断煤层是否具有突出危险性的瓦斯压力临界值为0.74 MPa，故选取瓦斯压力不大于0.74 MPa的区域为有效抽采区域。为了研究煤层渗透率对钻孔有效抽采半径的影响，将煤层原始瓦斯压力定为1.2 MPa，将煤层初始渗透率定为0.01，0.505，1 mD。由图5可知，(云图为不同初始渗透率条件下瓦斯抽采180 d时钻孔周围瓦斯压力分布)，3种煤层初始渗透率条件下，抽采180 d时钻孔的有效抽采半径分别为0.379，1.687，2.424 m。在相同的抽采条件下，煤层初始渗透率越大，瓦斯在裂隙中的运移速度越快，钻孔周围的瓦斯压力下降的越快，钻孔有效抽采半径也越大。相同初始渗透率条件下，钻孔有效抽采半径随抽采时间的增加逐渐增大，而煤体初始渗透率越大，钻孔有效抽采半径随抽采时间的增加幅度也越大。

图5 不同初始渗透率下有效抽采半径随时间变化Fig.5 Change of effective drainage radius with time under different initial permeability

煤层原始瓦斯压力越大，开采时发生煤与瓦斯突出的风险性也越高，将煤层中的瓦斯抽采至安全水平也越困难。为了研究煤层原始瓦斯压力对钻孔有效抽采半径的影响，将煤层初始渗透率定为0.505 mD，将煤层原始瓦斯压力定为0.9，1.2，1.5 MPa。图6为不同原始瓦斯压力条件下钻孔有效抽采半径随抽采时间变化柱状图，可以得出，在3种煤层原始瓦斯压力条件下，抽采180 d时钻孔的有效抽采半径分别为1.271，1.687，2.652 m。在同一抽采时间下，随着煤层原始瓦斯压力的增大，钻孔有效抽采半径越小。这是由于钻孔瓦斯抽采过程中，随着钻孔周围的瓦斯被抽采完毕，钻孔更远处的瓦斯也不断往钻孔周围流动，当煤层原始瓦斯压力越大，压力梯度也越大，钻孔周围的瓦斯不断从远处得到补充，钻孔周围瓦斯压力下降得越慢，将瓦斯抽采至安全水平需要的时间就越久。

图6 不同原始瓦斯压力下有效抽采半径随时间变化Fig.6 Column diagram of effective extraction radius changing with time under different original gas pressures

由图5～6可知，钻孔有效抽采半径与抽采时间成正相关关系，但它们的关系却不是纯线性关系，而是随着抽采时间的增加，钻孔有效抽采半径增加量越来越小，并逐渐趋近于某1个值。这是因为随着钻孔周围的瓦斯被抽采，抽采负压不能提供离钻孔更远处的瓦斯流动至钻孔所需的压差，离钻孔更远处的瓦斯无法被抽采至钻孔，钻孔抽采半径增加量不断变小。因此，瓦斯抽采过程中，煤层初始渗透率的影响最为显著，而煤层增透措施对于瓦斯抽采效果提升具有显著作用。

2.2 多因素交互影响的响应曲面模型

响应曲面法通过在多元线性回归的基础上主动收集数据，以获得具有较好性质的回归方程。以煤层初始渗透率、原始瓦斯压力及抽采时间3种因素为自变量，钻孔有效抽采半径为响应值，通过Design-Expert软件采用Box-Behnken方法设计3因素3水平的响应面试验方案，设计方案共15种，运用COMSOL模拟软件解算数值模型，得到15组试验的钻孔有效抽采半径(响应值)，试验设计方案及响应值如表1所示，表中因素的取值均有1个水平为现场参数，其他水平通过等差赋值合理获得。

由表1可知，采用响应面优化设计方法开展多元回归拟合分析，建立目标函数有效抽采半径R与煤层初始渗透率K、原始瓦斯压力P以及抽采时间T的多项式响应曲面回归方程。但若采用大于二阶多项式的响应面模型会使得高次项系数的数目增大，增加计算量，故在实际应用中多采用二次多项式，其高次项系数数目不多，且对响应曲面模型的拟合精度较高。本文的二次多项式响应曲面模型如式(12)所示：

(12)

式中：R代表抽采半径；K代表煤层渗透率；P代表原始瓦斯压力；T代表抽采时间。式(12)中参数均为无量纲参数。

如表2所示，为回归方程的方差分析，表中P值是当模型假设(二阶响应面响应曲面模型的所有系数都为0)为真时所得样本观察结果或更极端结果出现的概率。如果P值很小，说明0假设情况发生的概率很小，根据小概率原理，可否定0假设。P值越小，说明该项越显著。

表1 钻孔有效抽采半径响应试验设计方案及结果Table 1 Design scheme and results of response test for effective drainage radius of boreholes

由表2可知，响应曲面模型P值远小于0.05，表明响应曲面模型显著性极好，所得方程可准确反映各因素

表2 方差分析Table 2 Analysis of variance

对钻孔有效抽采半径的影响。模型中的煤层初始渗透率项、原始瓦斯压力项、抽采时间项、煤层初始渗透率平方项、原始瓦斯压力平方项、渗透率与原始瓦斯压力交互项及渗透率与抽采时间交互项的P值都小于0.05，表明这几项在模型中都是显著的。响应曲面模型的决定系数为0.990 8，表明99.08%以上的响应值均可由该模型解释，模型调整后的决定系数为0.974 3，模型的预测决定系数也达到了0.853 4，表明响应曲面模型的准确性良好。

2.3 响应曲面模型的验证

为了验证二次项响应曲面模型函数表达式的准确性，选取6组不同参数条件，通过响应面模型函数表达式预测得出钻孔有效抽采半径，再运用COMSOL软件模拟得到不同试验条件下的钻孔有效抽采半径，将二者的结果进行对比，验证响应面模型函数表达式的准确程度。

由表3可知，响应面模型的函数表达式在预测不同参数条件下的钻孔有效抽采半径有一定的准确性，在随机的6组试验条件中，有效抽采半径的预测值与模拟值的最大误差值为0.133 m，最小的误差值为0.005 m，除了第1组的误差率达到20.7%，其他组的误差率基本都在15%以下，模型预测准确度基本可达85%以上，整体预测效果良好。响应面模型的函数表达式可以预测在不同参数条件下钻孔的有效抽采半径，为各种条件下钻孔的布置起到借鉴的作用，为煤矿井下瓦斯治理提供理论指导。

表3 函数模型预测值与模拟值对比Table 3 Comparison between predicted and simulated values of function model

2.4 多因素交互影响机制分析

为了探究多因素交互作用下钻孔有效抽采半径的影响机制，针对本文研究的3个因素，给出基于2个自变量的响应曲面三维图，另一个变量设定为中间水平值。如图7所示，为抽采时间120 d时，煤层初始渗透率与原始瓦斯压力的响应曲面图。可以看出，煤层初始渗透率与有效抽采半径成正相关关系，原始瓦斯压力与钻孔有效抽采半径成负相关关系，这与单因素分析的结果相同。同时，当煤层初始渗透率为0.01 mD时，原始瓦斯压力从0.9 MPa增加到1.5 MPa，有效抽采半径从0.551 m减小到0.276 m，降低幅度为49.91%；当煤层初始渗透率为1 mD时，原始瓦斯压力从0.9 MPa增加到1.5 MPa，有效抽采半径从3.079 m下降到1.468 m，降低幅度为52.32%。说明煤层初始渗透率对有效抽采半径的影响程度要大于原始瓦斯压力，煤层初始渗透率的增加能够放大原始瓦斯压力对有效抽采半径的影响。当原始瓦斯压力为0.9 MPa时，煤层初始渗透率从0.01 mD增加到1 mD时，有效抽采半径增加2.528 m；当原始瓦斯压力为1.5 MPa时，煤层初始渗透率从0.01 mD增加到1 mD时，有效抽采半径增加1.192 m，说明原始瓦斯压力的增大会降低煤层初始渗透率对有效抽采半径的影响。

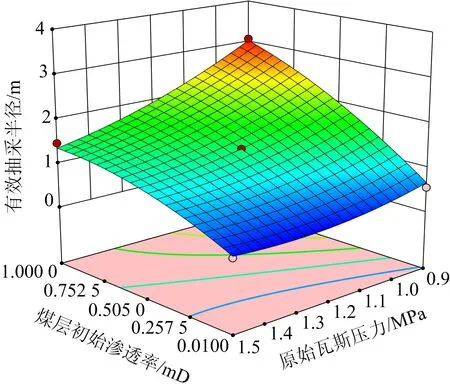
图7 煤层初始渗透率与原始瓦斯压力的响应曲面Fig.7 Response surface diagram of initial permeability of coal seam and original gas pressure

如图8所示，为煤层初始渗透率与抽采时间的响应曲面图(原始瓦斯压力为1.2 MPa)，可以看出，煤层初始渗透率和抽采时间都与有效抽采半径呈正相关关系。当煤层初始渗透率分别为0.01，1 mD时，抽采时间从60 d增加到180 d，有效抽采半径分别增加0.098，1.034 m，增加幅度分别为32.78%，74.44%。说明煤层初始渗透率的增加可以放大抽采时间对有效抽采半径的影响。当抽采时间为60 d时，若煤层初始渗透率从0.01 mD增加到1 mD，有效抽采半径增加1.090 m；当抽采时间为180 d时，煤层初始渗透率从0.01 mD增加到1 mD，有效抽采半径则增加2.026 m，说明抽采时间的增加会放大煤层初始渗透率对有效抽采半径的影响，煤层初始渗透率与抽采时间之间存在正反馈关系，都能促进对方对有效抽采半径的影响。

图8 煤层初始渗透率与抽采时间的响应曲面Fig.8 Response surface diagram of initial permeability of coal seam and drainage time

如图9所示，是煤层初始渗透率为0.505 mD时，原始瓦斯压力与抽采时间的响应曲面图，从图中可以看出，抽采时间对有效抽采半径呈正相关关系，原始瓦斯压力则相反。当原始瓦斯压力为0.9 MPa时，如果抽采时间从60 d增加到180 d，有效抽采半径从1.534 m增加到2.652 m，增加幅度为72.88%；当原始瓦斯压力为1.5 MPa时，如果抽采时间从60 d增加到180 d，有效抽采半径从0.737 m增加到1.271 m，增加幅度为42.01%。说明原始瓦斯压力的增加会降低抽采时间对有效抽采半径的影响。当抽采时间分别为60，180 d时，原始瓦斯压力从0.9 MPa增加到1.5 MPa，有效抽采半径分别降低0.797，1.381 m，降低幅度分别为51.96%，52.07%。说明抽采时间的增加会略微放大原始瓦斯压力对有效抽采半径的影响。

图9 原始瓦斯压力与抽采时间的响应曲面Fig.9 Response surface diagram of original gas pressure and drainage time

3 结论

1)根据响应曲面试验分析，瓦斯抽采参数对钻孔有效抽采半径影响显著性的顺序为：煤层初始渗透率、原始瓦斯压力、抽采时间。煤层初始渗透率与有效抽采半径成正相关关系，煤层初始渗透率越大，瓦斯在裂隙中的运移速度越快，有效抽采半径亦越大。在同一抽采条件下，随着煤层原始瓦斯压力的增大，钻孔有效抽采半径变小。有效抽采半径与抽采时间成正相关关系，但非线性相关，随着抽采时间增加，钻孔有效抽采半径逐渐趋近于某一定值。

2)钻孔有效抽采半径对多因素交互影响的响应曲面模型为：R=2.49+4.469K-4.66P+0.0133 5T-0.98K2+2.111P2-2.247K×P+0.007 86K×T-0.008 11P×T，响应曲面模型P值远小于0.05，该响应曲面模型显著性极好，响应曲面模型的决定系数为0.990 8，故99.08%以上的响应值均可由这个模型解释。

3)煤层初始渗透率的增加能够放大原始瓦斯压力和抽采时间对有效抽采半径的影响，当煤层初始渗透率分别为0.01，1 mD时，原始瓦斯压力从0.9 MPa增加到1.5 MPa，有效抽采半径的降低幅度分别为49.91%，53.32%；当煤层初始渗透率分别为0.01，1 mD时，抽采时间从60 d增加到180 d，有效抽采半径的增加幅度分别为32.78%，74.44%；而原始瓦斯压力的增大会降低煤层初始渗透率和抽采时间对有效抽采半径的影响，当原始瓦斯压力分为0.9，1.5 MPa时，煤层初始渗透率从0.01 mD增加到1 mD，有效抽采半径分别增加2.528，1.192 m；当原始瓦斯压力分为0.9，1.5 MPa时，抽采时间从60 d增加到180 d，有效抽采半径增加幅度分为72.88%，42.01%。瓦斯抽采过程中，煤层初始渗透率的影响最为显著，故对于低渗煤层瓦斯抽采，煤体卸压增透是提高抽采效果的重要方法。