基于改进OSV分解模型的图像分割

郭雨莹，许建楼,尚婉清，尤少培，王海军

(河南科技大学 数学与统计学院，河南 洛阳 471023)

0 引 言

图像分割是计算机视觉和图像处理中一个基本但仍然具有挑战性的问题。一般来说，图像分割是基于相似的属性(如强度、颜色和纹理)将图像分成一定数量的互不相交有不同特点的区域的过程,它在生物医学[1]和深度学习[2]等领域有着广泛的应用。通常，自然图像中的颜色和纹理特征非常复杂，因此从背景中完全分割对象非常困难。到目前为止，人们已经提出了很多图像分割模型。大体上，求解分割模型的方法分为基于模型[3-9]和基于学习[10-12]2大类。然而，由于图像的多样性和复杂性，使得统一的网络架构不能令大量图像产生一致最优分割效果。在训练网络过程中表现就是虽然所有训练样本的总的损失函数很好地达到极小值，但对于单个图像，损耗可能会随着训练的继续而增加。由于这种不稳定性以及深度学习的方法涉及大量数据，本文选择用基于模型的方式进行图像分割。

在已经提出的各种基于模型的图像分割方法中，最有效的方法是基于变分的分割方法。它利用原始图像定义一个体现分割区域的内部特点及边界的能量泛函，然后最小化该能量泛函实现图像分割。Mumford-Shah[3]模型是在每个区域内使用平滑函数进行近似，相当于将图像分割成不同的同质区域，但其非凸的能量泛函使得极小化问题难以用数值方法分析和求解。文献[4]提出了用每个区域内的常值函数来近似图像的活动轮廓模型。文献[5]将图像分割和图像去噪任务统一到一个全局最小化框架中，避免了水平集方法中初始化距离函数中的活动轮廓以及在进化过程中周期性地重新初始化距离函数中的活动轮廓。文献[6]为了能够处理分割中的灰度不均匀性，提出了一种新的图像分割的水平集方法。文献[7]在隶属函数上引入了一个非凸正则化，提出了一种新的用于软多相图像分割的变分模型。文献[8]采用一个多层水平集函数的N层水平集隐式曲面，将图像划分为N个区域，通过对一个水平集函数求极值，实现三维多相分段常值图像的快速分割与重建。与图像分割不同，图像分解技术是通过设计模型和算法，提取图像中的主要特征或者有用的信息，其主要目标是把一个给定的原始图像分解为卡通部分和纹理部分。现有的部分图像分解变分模型中使用了OSV模型中的H-1泛函[13-15]。由于在测量振荡分量时使用了H-1(Ω)中的弱范数，这些模型可以有效地从输入图像中提取纹理(详细介绍参见文献[16]第3节)。虽然这些方法在视觉上都取得了很好的分解效果，但是这些模型在求解过程时都忽略了Hodge分解得到的向量函数q。从数学的意义上来说，若忽略向量函数q包含的向量信息，则模型的能量泛函出现偏差，影响结构纹理分解。因此，文献[17]保留了向量函数q，同时让纹理对应的向量场属于L1空间，提出了加权曲率驱动的卡通纹理图像分解。

由于自然图像不符合分片常数的假设，文献[18]将图像分解技术引入图像分割模型中，使用结构部分代替分割模型中的原始图像。文献[15]遵循织物图像可以分解为卡通和纹理成分的假设，在图像分割阶段结合了图像分解过程。文献[19]将图像分割和卡通纹理分解相结合提出了一种新的模糊分割模型。考虑到OSV分解变分模型中零散度向量函数被忽略的问题，本文保留了OSV模型中的零散度向量函数，将改进后的图像分解项加入分割模型，给出了一种更合理、更有效的图像分割模型和分割算法。由于新模型保留了图像分解变分模型中的零散度向量函数，使得本文方法能够正确分割较复杂的自然图像。

1 模型准备

1.1 图像分割模型

给定原始图像f(x):Ω→R+∪{0}，假定图像分割区域数为N已知，文献[20]提出以下的基于模糊区域的多相图像分割模型:

(1)

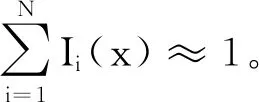
1.2 图像分解模型

文献[21]提出了一个在图像分解中广泛应用的变分模型，简称OSV模型：

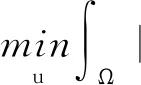
(2)

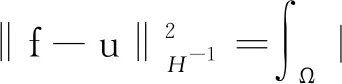
1.3 基于图像分解的分割模型

由于自然图像通常有结构和纹理2种成分，文献[18]将分解模型(2)加入分割模型，提出了基于图像分解的稀疏正则化多区域图像分割方法：

(3)

式中：第1项是正则项;第2项是保真项;第3、4项为图像分解项;(Ii)γ表示隶属度函数Ii(x)的多尺度小波分解系数;λ、α、β是正的平衡参数。该模型将分解模型与分割模型相结合，在图像分解的同时进行图像分割，从而得到较好的分割结果。

2 本文模型及算法

2.1 新模型

在式(2)第2项的推导过程中，作者在文献[21]中假设图像的纹理v=f-u=divg，然后利用g的Hodge分解g=∇p+q，忽略q并令g属于L2空间而得到，其中div是散度算子，p是标量函数，q是零散度向量函数。然而忽略q，则g的向量信息被改变，进而改变了纹理的特性[17]。

自然图像一般有结构和纹理2种成分，使用分块常值函数并不能很好地逼近原始图像。考虑到现有的使用H-1泛函的模型在求解过程中都忽略了Hodge分解得到的零散度向量函数，本文提出了保留零散度向量场约束的多区域图像分割模型：

(4)

注意到，与模型(3)不同，新模型(4)中图像分解项保留了无散度向量场q，这是本文的主要贡献。首先，新模型(4)中第四项是g属于L2空间，不同于文献[17]让g属于L1空间。其次，新模型(4)和模型(3)虽然从表达式v=divg的形式上看是一样的，但是在式(3)中g是与结构部分u直接相关的。事实上，由于忽略无散度向量函数q使得g=∇(Δ-1(f-u))不准确，则由模型(3)所得的结构部分u不准确，而本文提出的模型(4)保留了零散度向量场q，保证了向量场g的准确性，从而得到更准确的结构部分u，因此得到的分割结果更好。

2.2 模型算法

对模型(4)，采用增广拉格朗日乘子法和交替方向法。首先引入2个辅助变量hi、z，令hi(x)=Ii(x)，z=Δ-1(f-u)，则模型(4)变成以下最小化问题：

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

对u子问题，用直接变分法得到它的Euler-Lagrange方程，再利用梯度扩散流得：

(17)

对mi子问题，这是一个关于mi的可微优化问题，可得到解的显示表达式：

(18)

对Ii-子问题，这是一个关于Ii的可微优化问题，可得到解的显示表达式：

(19)

对q子问题，利用直接变分法的下面方程并用快速傅里叶变换求解：

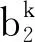
(20)

对z子问题，用直接变分法的如下方程并用快速傅里叶变换求解：

(2βΔ-μ3Δ2)z=-2βdivqk+1-

(21)

(22)

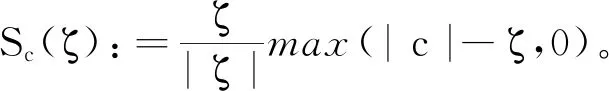
3 实验结果及分析

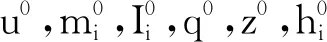
(a) 自然图像 (b) Fish图像 (c) 织物图像 (d) Plaid图像

为了说明本文模型的可行性和有效性，对以上测试图像进行仿真实验。参与实验的其他模型主要有文献[6]、[22]，基于图像分解使用了H-1泛函的分割模型文献[15]以及[18]。每个模型均通过人工调整参数达到最好的分割效果。在数值实验中，直观地给出纹理所对应的向量场g以及向量场q，同时进行定量分析来说明本文模型的创新。

3.1 两相分割实验

图2为自然图像在文献[15]、[18]以及本文模型上的分割实验结果。其中，Ii,i=1,2指示图像的分割子区域。

(a) 文献[15] (b)文献 [18] (c) 本文模型

从图2可以看出，其他对比模型的分割子区域I2包含一些不需要的纹理信息。这是因为尽管文献[15]和[18]引入OSV分解项得到了相对较好的图像分割结果，但OSV分解项忽略了零散度向量场，使得分解不准确，进而导致分割结果I2中仍包含部分纹理信息。而本文模型保留了被忽略的零散度向量函数q，使得纹理对应的向量场更准确，从而通过求解模型得到了更加准确的结构和纹理图像，因此分割结果I2较为理想。另外，由于零散度向量场还包含很多向量信息(如图4)，与其他忽略q的模型相比，本文模型的向量场g更加清晰准确，包含更完整的纹理信息，故本文模型的分解结果较为理想。

同样地，为了进一步验证本文模型的有效性，文献[6]、[22]、[18]以及本文模型在Fish图像上进行对比分割实验，得到的结果见OSID“开放科学数据与内容”中“补充材料.docx”的图1。

3.2 三相分割实验

图3选择织物图像作为测试图像对文献[15]、[18]的模型和本文模型进行实验，展示了相应的分割结果、分解结果及其对应的向量场g。其中，Ii,i=1,2,3指示图像的分割子区域。由于文献[6]、[22]直接对织物图像进行分割，且实验结果相对较差，具体分割结果见OSID“开放科学数据与内容”中“补充材料.docx”的图2。

(a)文献 [15] (b) 文献[18] (c) 本文模型

从图3可以看出，相较于其他对比模型，本文模型的分割结果更准确。由于织物图像含有大量纹理成分不利于分割，文献[15]和[18]在分解的同时也进行了分割从而得到了较为准确的分割结果，但其分解过程忽略了零散度向量函数q，导致纹理所对应的g向量场不正确，使得通过求解模型得到的结构成分和纹理成分不准确，因此得到的分割子区域L1包含一些属于子区域L3的线条。而本文模型的向量场g保留了零散度向量场q(如图4)，∇z向量方向与q向量方向相互抵消合并，使得纹理部分提取得比较彻底，卡通部分更加符合分段常数的假设，进而得到了更好的分割结果。

类似地，文献[15]、[18]、[6]以及本文模型在Plaid图像上进行分割实验，得到的结果见OSID码“开放科学数据与内容”中“补充材料.docx”的图3。

(a) 自然图像 (b) Fish图像 (c) 织物图 (d) Plaid图

从图4可以看出，q向量场包含了很多向量信息。如果q被忽略，那么得到的g向量场就不正确，从而影响通过模型求解得到的结构部分和纹理部分的准确性，进而影响图像分割的结果，因此保留q是有必要的。

3.3 分割结果的客观评价

为了进一步说明新模型的优势，采用精确率[23]、召回率[24]以及Jaccard相似系数[25]来评估分割结果，如表1所示。

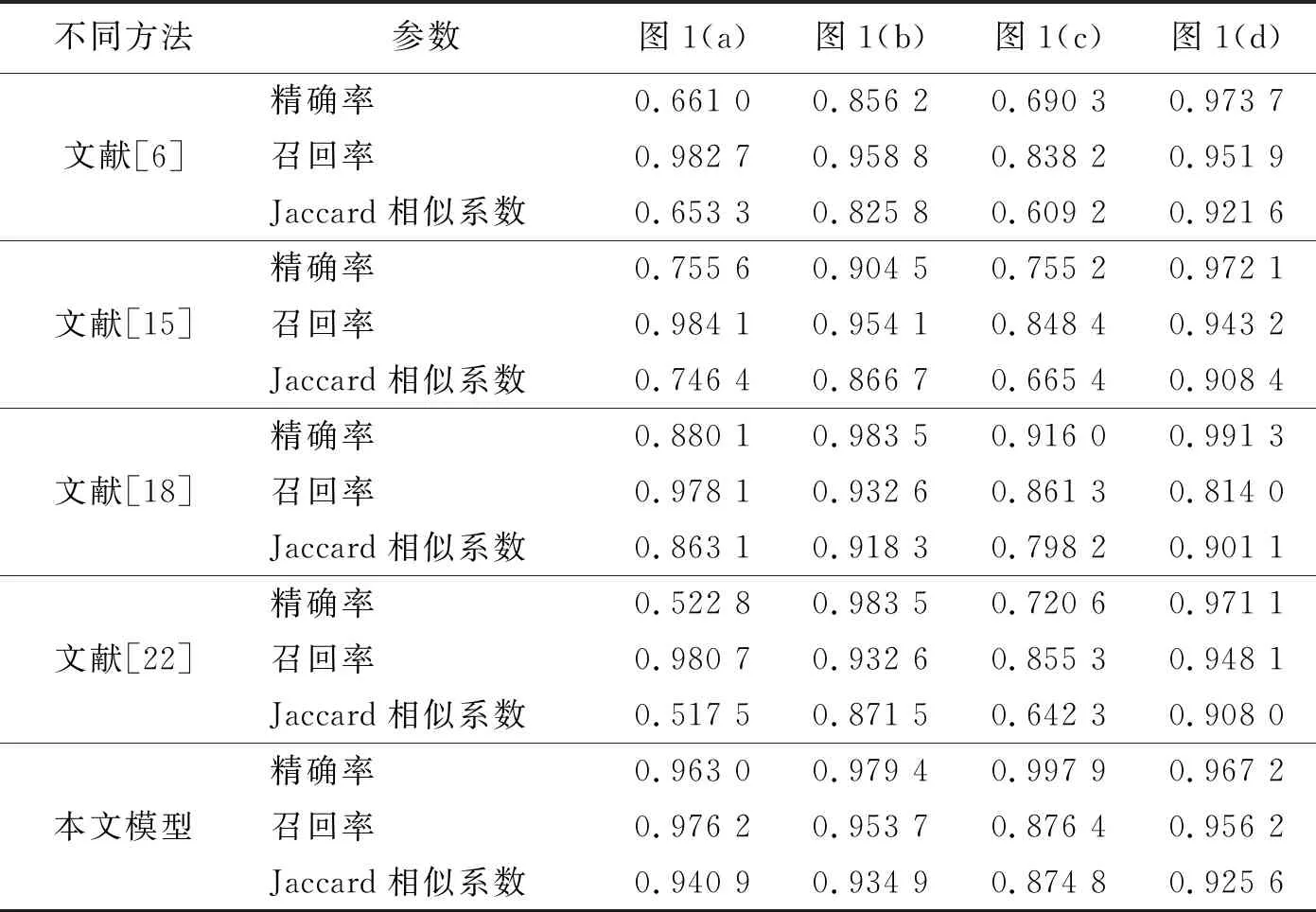
表 1 客观评价结果

表1中的指标越接近1，说明分割越准确。从表1可以看出，文献[6]、[22]的3种评价指标数值上表现较差，由于OSV分解项的加入，文献[15]、[18]的3种评价指标数值上表现较好，而本文模型保留了OSV分解项忽略的q，在数值上表现更好。与其他模型相比，本文模型在测试图像上精确率、召回率以及Jaccard相似系数的平均值至少分别提高了3.42%、0.77%、4.89%。这与本文模型的理论分析和直观视觉结果一致。

4 结 语

为了得到更好的分割结果，本文通过分析无散度向量场理论，提出了一个新的带有零散度向量场约束的基于图像分解的多区域分割模型并采用交替方向法求解新模型。实验结果表明，对于纹理图像，由于耦合图像分割与图像分解使得分割不易受纹理影响，从而新模型的分割结果在精确率、召回率、Jaccard相似系数上有明显提升，由于保留了使用H-1泛函度量振荡成分时忽略的无散度向量场q，无论从理论还是数值实验，向量信息都更加完整。