分数阶中立型随机时滞微分方程解的存在唯一性

李佳敏，丁小丽，王苗苗

(西安工程大学 理学院 陕西 西安 710048)

0 引 言

分数阶微积分理论在生物学，力学，电路等领域有广泛的应用[1-3]，有关分数阶微分方程的研究引起了人们高度重视。由于现实中的一些模型用确定性的分数阶微分方程，或者用整数阶随机微分方程很难模拟，所以有必要将二者整合起来，进一步深入研究分数阶随机微分方程，使之应用于更为广泛的领域。关于分数阶随机微分方程解的首要问题是研究其存在的唯一性，然后尝试能否求得该解并探索其相关性质。黄鹤皋讨论了分数阶随机微分方程解的存在唯一性[4]；MOUALKIA等讨论一类分数阶变阶随机微分方程解的存在唯一性，用Picard迭代法证明解的存在性，并提出了唯一性的充分条件[5]。

中立型随机微分时滞方程是依赖于过去值和现在值的随机方程，但又涉及到带有时滞的导数以及函数本身。证明这类方程解的存在性和唯一性主要是通过Banach不动点定理和Picard迭代法等2种不同的方法进行的。BENCHOHRA等利用Banach不动点定理研究了分数阶泛函微分方程和中立型泛函微分方程无穷时滞解的存在性[6]; 程烨等运用Schauder不动点定理和Banach不动点定理证明了一类分数阶中立型泛函微分方程初值问题解的存在唯一性[7];在相同思路下，LU等得到了一个保证平凡解均方渐近稳定的充分条件[8]；AGARWAL等讨论了一类具有有界时滞的分数阶中立型泛函微分方程的初值问题[9]。Picard迭代法也是一种很重要的近似计算方法。张远程等用经典的Picard迭代法研究了中立型随机泛函微分方程解的存在唯一性，其实质就是将微分方程转化成与之等价的同解积分方程，然后证明该方程解的存在唯一性[10]; 在此基础上，ZHOU等讨论了一类具有无穷时滞的分数阶中立型泛函微分方程的初值问题，得到了解的存在唯一性的判据[11]。这些研究为分数阶中立型随机时滞微分方程解的证明提供了理论支持。

分数阶中立型泛函微分方程是一类特殊的分数阶微分方程[12]。张志信等用分步法研究了分数阶中立型泛函微分方程初值问题解的存在唯一性[13]。DING等通过引入与Mittag-Leffler函数相关的积分算子，给出了一种证明分数阶随机微分方程解存在唯一性的新方法。算子和积分不等式为微分方程解的存在性、唯一性、稳定性等性质的研究提供了有效途径[14-16]。不过，分数阶中立型随机时滞微分方程解的存在唯一性的证明还有待完善。本文将分步法以及Picard迭代法引入分数阶中立型随机时滞微分方程，并利用算子以及中立项的性质解决解的存在唯一性问题。

1 预 备

定义1[17]设0<α≤1,t∈Ω,函数f(t)∈L1(Ω;Rn)的α阶Riemann-Liouville型分数阶积分定义为

其中Γ(·)是Gamma函数。

性质1[18](It积分的等距性) 设G∈L2(Ω;Rn)，则G在Ω上关于m维标准Brown运动{B(t,ω):t≥0}的It积分为

其中E为期望。

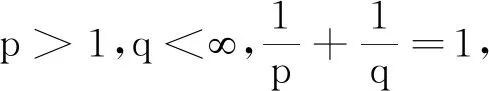
引理2[19-20]设0<α<1,a(t)是在时间区间Ω上的局部可积的非负函数,b(t)、g(t)是在Ω上的非负非减且有界的连续函数，如果v(t)非负，在Ω上局部可积, 且满足

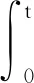
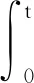
则

推论1[19]假设满足引理2中的条件,且a(t)在Ω上非减,则

式中:Eα为Mittag-Leffler函数,

定义3[18]为了证明方程(1)解的存在性，定义2个算子J1、J2分别为

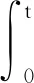
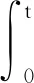
式中：0<α≤1；φ(t)∈C(Ω;Rn)。

引理3[18]设0<α≤1,φ(t)∈C(Ω;Rn),则

(J1J2φ)(t)=(J2J1φ)(t)

引理4[18]设0<α≤1,φ(t)∈C(Ω;Rn),i=1,2,3，…,有下列关系成立:

2 解的存在唯一性

考虑如下形式的分数阶中立型随机时滞微分方程:

(1)

式中：τ>0为给定的时滞量；f,σ∈C(Rn×Rn×[0,T]；Rn)；g∈C(Rn×Rn×[0,T];Rn×m)是Borel可测函数D∈(Rn;Rn)为中立项；

B(t)=(B1(t),(B2(t),…,Bm(t))T

是在完备概率空间{Ω,F,P}上的m维布朗运动;ζ∈C([-τ,0];Rn)，且E|ζ(θ)|2<∞;x、ζ分别为n维向量x、ζ的集合表示。

2.1 2个基本假设

为了证明解的存在唯一性，需要以下假设：

假设1假设M∈(0,1)，∀φ,φ∈C([-τ,T];Rn)及m，n∈R,有

|D(φ)-D(φ)|≤M‖φ-φ‖

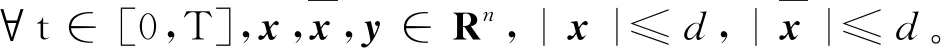
1) Lipschitz条件

2) 线性增长条件

|f(x,y,t)|2≤K(1+|x|2+|y|2)

|g(x,y,t)|2≤K(1+|x|2+|y|2)

|σ(x,y,t)|2≤K(1+|x|2+|y|2)

2.2 存在唯一性证明

首先在区间[0,τ]上讨论五步法，证明解的存在唯一性。当t∈[0,τ]时，

第1步: 方程(1)可变形为

第2步: 对于k=0,1,2,…,构造Picard迭代序列{xk+1(t)}:

xk+1(t)=ζ(0)+D(xk(t-τ))-D(x(-τ))+

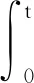
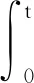
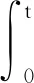
利用数学归纳法证明xk+1(·)∈M2([-τ，T];Rn)。当k=0时，显然可以得到x1(t)=ζ(0)-D(x(-τ))∈M2([-τ,T];Rn)。不妨设xk(t)∈M2([-τ,T];Rn)，将验证xk+1(t)∈M2([-τ,T];Rn)。

E|xk+1(t)|2≤6E|ζ(0)|2+

6E|D(xk(t-τ))-D(x(-τ))|2+

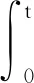
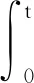
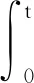
|σ(xk(s),xk(s-τ),s)|2ds≤

6E|ζ(0)|2+6M2E|xk(t-τ)-x(-τ)|2+

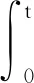
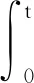
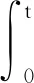
E|xk(s-τ)|2)ds≤

6E|ζ(0)|2+12M2E|xk(t-τ)|2+

12M2E|x(-τ)|2+

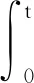
E|xk(s-τ)|2]ds+

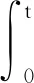
E|xk(s-τ)|2]ds

由于ζ(0)∈M2([-τ,T]；Rn),xk(t)∈M2([-τ,T];Rn)，因此xk+1(t)∈M2([-τ,T]；Rn),即xk(t)∈M2([-τ,T];Rn)。

第3步: 证明序列{xk(t)}在区间[0,T]上一致收敛。

令ek+1(t)=E|xk+1(t)-xk(t)|2,则

根据算子J1、J2的定义，

由文献[14]中的性质2.2可以得到，J1、J2对φ(t)∈C(Ω;Rn)是非递减的。对k进行数学归纳可知

由引理3知J1、J2可交换,由文献[14]中的性质2.1知J1、J2是定义在C(Ω;Rn)上的紧算子,且σ*(J1)=σ*(J2)={0},其中σ*(·)表示算子的谱,因此{xk(t)}是Cauchy序列,即Picard迭代序列{xk(t)}在区间[0,T]上均方一致收敛。

第4步:证明序列{xk(t)}的极限是方程(1)的解。

x(t)=ζ(0)+D(x(t-τ))-D(x(-τ))+

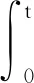
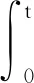
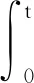
第5步: 证明方程(1)具有唯一解。

利用(a+b+c)2≤3|a|2+3|b|2+3|c|2,其中a,b,c∈R以及Hölder不等式、It积分的等距性、Lipschitz条件和假设1，得

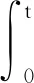
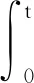
I1+I2

其中：

由引理2得

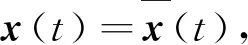
当t∈[τ,2τ]时,前4步方法与上述相同。

第5步: 证明方程(1)具有唯一解。

利用(a+b+c)2≤3(a2+b2+c2)、Hölder不等式、It积分的等距性、Lipschitz条件和假设1，得

其中：

|σ(x(s),x(s-τ),s)-

由引理2得，

当t∈[τ,2τ]时,方程(1)的解存在且唯一。

以此类推,当t∈[(n-1)τ,nτ]时,方程(1)解存在且唯一。故t∈[0,T]时，方程(1)的解存在且唯一。证毕。

注记1在分数阶随机时滞微分方程的基础上，增加中立项以及有关中立项的假设，即推广了文献[18]的结论。

3 结 语

研究了分数阶中立型随机时滞微分方程解的存在唯一性问题。利用分步法思想，在各个区间逐一进行讨论，且结合Picard迭代法以及积分算子理论，增添算子,证明分数阶中立型随机时滞微分方程解的存在性和唯一性。使得分数阶中立型随机时滞微分方程解的存在唯一性的证明更加简洁,同时也为后续研究波形松弛方法求解分数阶中立型随机时滞微分方程打下基础。