改进协同进化算法求解柔性车间调度问题
李睿祺,毛剑琳,伍 星,3,张 亮
(1.昆明理工大学 机电工程学院,云南 昆明 650500;2.昆明理工大学 信息工程与自动化学院,云南 昆明 650500;3.云南机电职业技术学院,云南 昆明 650500)
0 引 言
车间调度问题主要分为作业车间调度(job-shop scheduling problem,JSP)问题与柔性作业车间调度(flexible job-shop scheduling problem,FJSP)问题两种,JSP是一种最经典、最具有代表性的问题模型,而随着生产力的发展,不同工序对机器的要求越来越小这也让FJSP问题变为目前生产调度中最常见的模型.FJSP是属于NP-hard问题范畴[1],在各工件的各工序中的机器约束不唯一,但是更适合于当前小订单、多品种的生产要求,同时这也使得问题更加复杂.
经过近40多年的研究产生了很多求解车间调度的方法.如陶继平[2]用拉格朗日松弛法求解柔性调度问题;轩华等[3]使用动态规划的方法求解云资源调度问题,此类把调度问题基于运筹学建立数学规划模型求解调度问题的方法能够有效地解决小规模调度模型,但是很难求解大规模调度模型.鄢传睿[4]使用人工智能的方法基于B/S的智能仓储管理系统设计了调度专家系统求解调度问题,这类方法虽然效果较好但是存在鲁棒性不足、开发费用过高等问题.段世豪[5]通过把深度学习神经网络算法、长短时记忆神经网络应用到线缆企业的生产数据预测中,此类方法为调度问题提出了一种全新的解决方案但此方法计算效率相对较低、变量太多,在实际的调度问题中很难进行实现.目前求解调度问题使用最多、效果最好的是用智能优化算法来求解,如:姜天华[6]提出一种改进灰狼群算法求解柔性车间调度问题;王雷等[7]提出了一种具有双种群的遗传算法求解柔性车间调度问题;Xing等[8]提出了一种具有知识体的学习型蚁群算法求解柔性车间调度问题.上述的智能优化算法具有普遍适用性和较低的经验复杂性等特点,但没有一种算法可以完美地求解出所有不同模型的问题.故将两种算法互相结合、取长补短可以有效改善算法的性能,近年来各种算法的混合也成为了热点研究方向,如Li等[9]提出了一种将禁忌搜索法和遗传算法相结合的混合算法求解车间调度问题.
以上算法在求解FJSP问题模型时虽然一定程度上能够求出结果较好的解,但是随着算例数据的增大后解的空间模型也随之增大,算法在初期虽然会较快搜索,但后期其搜索能力会有所下降,在复杂度高的空间中容易陷入局部最优,无法兼顾算法的搜索能力与空间搜索能力.本文提出了一种基于GA和PSO的学习型协同进化算法,通过对其精英种群的深度搜索增强了算法的搜索能力,同时两个也保证了在复杂空间中种群的多样性,从而增加种群的空间搜索避免陷入局部最优,两个算法种群之间相互协同、竞争、信息交流增强了算法的搜索能力.最后通过对每一代中最优个体的染色体进行学习来影响新个体的生成,提取当前最优方案的信息特征提高了搜索的速度.通过实验表明学习型协同进化算法不仅在小算例中搜索结果优秀而且在大算例依然可以完成有较好的搜索表现.
1 柔性作业车间调度数学模型
FJSP问题是JSP问题的延伸,其主要区别是工序对加工机器的约束不唯一,这使得生产加工中若某台机器发生故障仍然不影响生产,提高了生产的柔性,同时提高生产效率,符合多品种、小批次、短周期的生产要求.其数学模型可以描述为n个工件在m台机器上加工,其中每个工件i包含有j个工序,第i个工件中的j个工序Oij至少具有一个加工机器m可以选择,其主要有以下约束:
1) 同一时刻一台机器只可以加工一台设备;
2) 同一工件的同一工序只可以在一台机器上进行加工,不可中断;
3) 同一工件的需要按照工序顺序进行加工;
4) 所有工件可以在零时刻开始加工.
目标函数:最大完工时间及对所有工件的最大完工时间求最小
(1)
约束公式如下:
公式(2)表示工序的加工开始时间必须在上一道工序的完工时间之后;
公式(3)表示机器只有在当前加工工序完成后才可以进行下一道工序的加工.
Eijk-Ei(j-1)≥Tij,1≤i≤n
(2)
Eegk-Eijk≥Tegk,1≤e≤n,1≤i≤n
(3)
2 基于邻域搜索的协同进化算法求解车间调度问题
2.1 问题的编码和解码
FJSP问题可以分为工序顺序和机器选择两个部分,故该问题编码方式为具有工序顺序和机器选择的整数编码.前段工序顺序染色体在解码过程中按照编码的先后顺序进行安排,后端的机器选择染色体是前段染色体里该工件中该工序的机器选择,分别为J11,J12,…,Jij在机器选择表中的位置点,其对应关系在解码中体现.
图1所示为3个工件且每个工序的机器选择分别为位置点3、2、2以此类推.
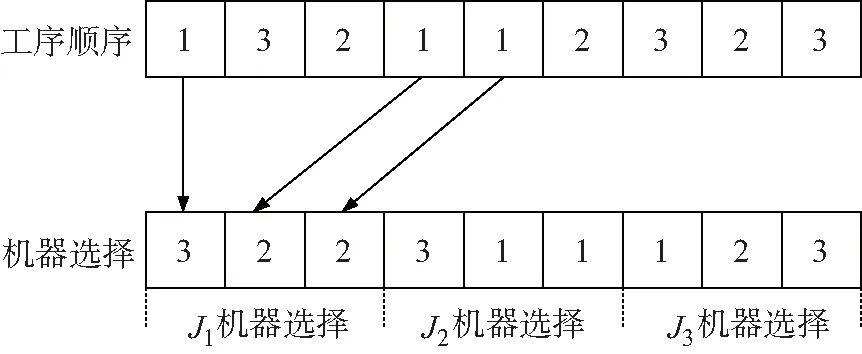
图1 编码方式Fig.1 Encoding
工件具有3个工序,其可选择机器选择位置点为3的染色体.前端染色体表示安排的加工顺序为J11、J31、J21、J12、J13、J22、J32、J23、J33,其工件1中3个工序的机器选择分别为位置点3、2、2;其工件2中3个工序的机器选择分别为位置点3、1、1,以此类推.
染色体的解码对编码不是一个单项传递信息的过程,不同的解码方式会对同一个染色体求解出不同的调度方案.常见的解码方式是按照染色体的工序顺序和机器选择信息来安排工件的加工方案,其在i工件中j工序的安排方案主要由以下两个约束所决定,并在T1、T2中选取最大时间安排该工序的加工.其中T1表示i工件的上一道i-1工序的完成时间,T2表示选择的机器M上上一个工件K的完成时间,如图2所示.
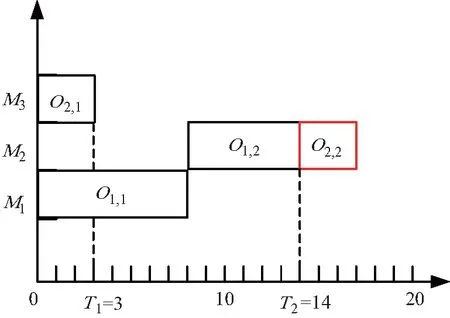
图2 普通解码方式Fig.2 Figure normal decoding
但是在约束(2)中可能存在机器M上的工件K前面有大段的空闲加工时间未安排,故本文提出了一种基于搜寻可插入时间段的贪婪解码方法,其约束只有(1)一个约束,在确定加工机器M后搜索满足约束(1)的可插入时间段进行插入.如图3所示,J22的安排仅需要满足约束(1)后搜索到可以插入的时间段安排工序O22,根据该解码方式求得最大完工时间为14.
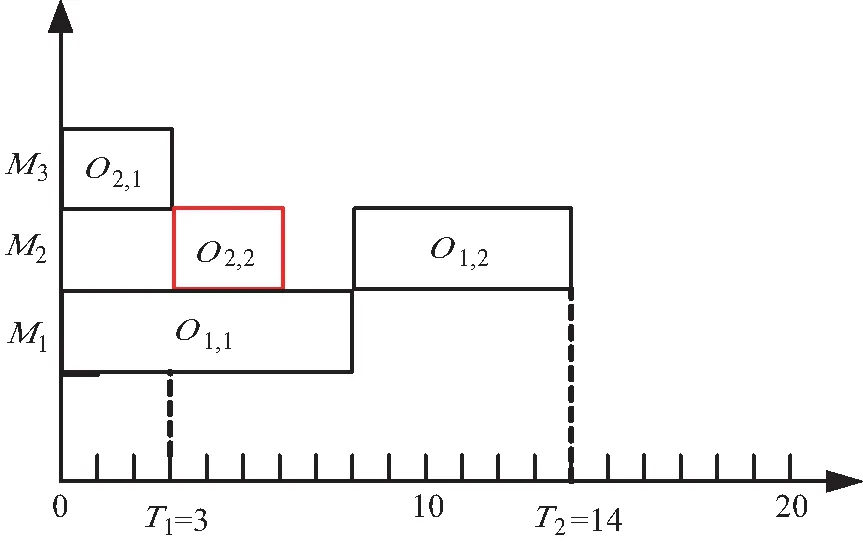
图3 基于时间段的贪婪解码Fig.3 Greedy decoding based on time period
2.2 GA和PSO的算法的协同
因GA和PSO两种算法是在车间调度运用最广且效果较好的算法,为使两算法特点相融,提高种群多样性、增加算法搜索能力,提出了一种基于GA和PSO的协同进化算法使两算优点相融合.
GA和PSO的染色体中机器选择编码方式都为随机生成一个可选机器范围内的随机数取整,其对应的数为选择的加工机器的位置点.
在加工顺序染色体中,GA储存工序数据方式为其数字代表工序矩阵中的位置点,如图4所示为GA工序数据储存方式.
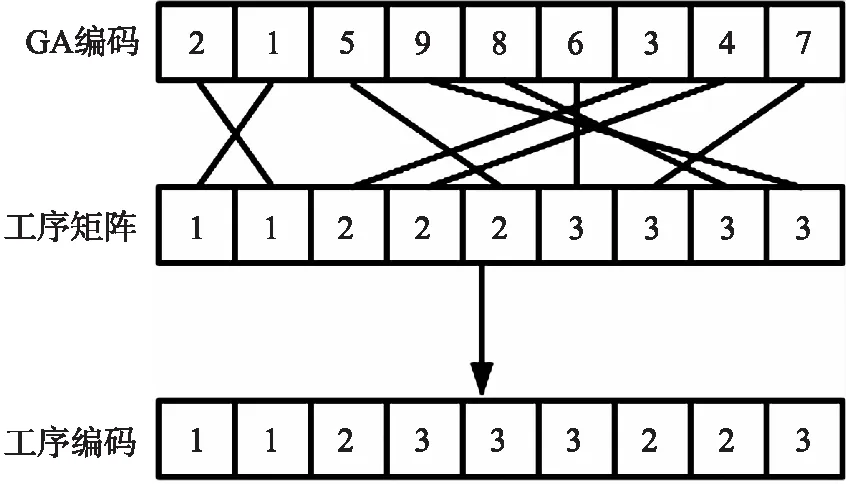
图4 GA数据储存方式Fig.4 GA data storage method
而PSO储存工序数据的方式为生成0~1内的随机数,并从小到大进行排序,其排序顺序为工序矩阵的位置点(与GA编码相同).如图5所示为相同的工序编码下PSO数据储存方式.
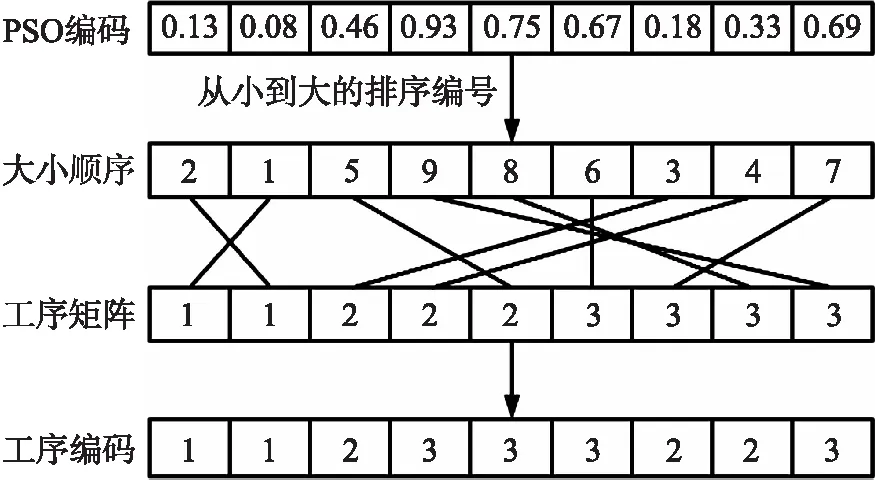
图5 PSO数据储存方式Fig.5 PSO data storage method
初始化种群时GA与PSO生成相同数量的染色体,每代为50个,在每一代的算法更新迭代后选出两种群中适应度值前10的染色体作为精英种群,通过变邻域搜索后更新精英种群.若GA种群中挑选的染色体为x个,则PSO种群挑选的个数10-x个.把其中x个遗传染色体的数据储存方式转换为PSO的编码方式,其转换步骤为:
Step1:随机生成M个0~1内的随机数,并从小到大进行排序;
Step2:排序顺序与GA编码中数字相同的随机数带入GA编码的位置.
再把10-x个PSO种群中的染色体转换为GA的编码方式,其转换步骤为:
Step1:对PSO工序顺序染色体中的随机数进行从小到大的排序;
Step2:排序后的大小顺序编码代入其PSO编码的位置.
这时精英种群中10个个体分别有了GA的编码方式和PSO的编码方式,使用GA的编码方式进行2.4章节中的变邻搜索,再根据上述步骤把GA编码转换为PSO的编码.最后分别把10个精英个体根据其编码方式对应加入到GA和PSO的种群中.通过两种群中信息的交互,使得两种群在共享中不断升值.
2.3 两种群的竞争淘汰机制
为使PSO与GA算法能够进行优胜劣汰的良性竞争,提高差的算法种群的质量,并增加一定的淘汰率使得步骤2.5中具有优秀知识的个体加入种群中,本文设计的淘汰机制有两种:
(1)当两个种群分别加入10个精英个体后,为保证种群数量不变,需淘汰适应最差的10个染色体.
(2)淘汰相同的染色体.
为了增加种群的淘汰率,保证新的具有优秀知识的个体加入GA种群中,故GA有10个染色体来自于前40个染色体中适应度前10的个体,保证使用淘汰机制(2)后GA种群的数量不足50.通过自然演化,若一种群效果比另一个算法效果好很多,则其精英个体可以全部替代另一种群中的最差个体,而自己的精英个体再替代自己的较差个体从而实现优胜劣汰的演化.
2.4 变邻域搜索
邻域搜索可以增强算法的搜索能力,针对该协同进化算法,对所有种群使用了文献[10]和[11]中提出的3种邻域结构(1)~(3)进行搜索,针对精英种群提出了2种遍历搜索的邻域结构(4)和(5)进行随机遍历搜索(本文中使用的随机概率为0.2),若适应度值更优则代替之前染色体,反之则不.
(1)VNS1:在工序顺序染色体让随机选择一段连续的染色体,进行倒转.
(2)VNS2:在工序顺序染色体上随机选择两个染色体进行位置交换.
(3)VNS3:在机器选择染色体上随机选择一个染色体使其选择时间最短的机器,若已是最短则不执行.
(4)VNS4:在工件顺序染色体上每个染色体有0.2的概率被选中,使其与其他所有的染色体互换一遍.
(5)VNS5:在机器选择染色体上每个染色体有0.2的概率被选中,使其把所有可选的机器号都选一遍.
2.5 根据最优个体生成新个体
针对编码中机器选择编码部分在算法后期,适应度较好的个体基本机器选择基本类似,故本文提出了一种对当前全局最优解进行机器选择知识学习的知识结构.在每一次迭代更新全局最优解后,机器的选择可能与上一代最优解的机器选择知识完全不同,故本算法使用的知识体仅为当前最优解的染色体.通过根据全局最优的机器选择部分染色体的位置点来提高下一代种群生成时机器选择染色体与全局最优相同的概率,从而根据全局最优解的机器选择知识来指导新种群生成的方向,增强种群的质量,提高收敛的速度,减少低效的搜索.
知识体结构如图6所示,当机器有J个选择位置,Xi为最优个体时,第i个工件的产生概率Px公式(4)、(5)为机器选择知识体的变更公式.
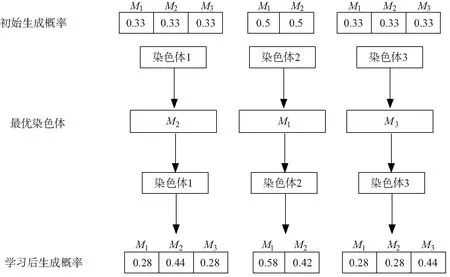
图6 知识体结构Fig.6 Body of knowledge
P(i)=P(i)+0.2
(4)
(5)
与文献[8]相比,本文知识体避免了在迭代后期部分机器选择概率收敛为1的情况.
2.6 算法框架
本文提出了一种基于GA和PSO的学习型协同进化算法.遗传算法中染色体共有50个,其中有40 个染色体是随机生成的,其中有10个个体是来自于前40个中适应度前10的染色体.这样即可以把优良的染色体保留下来,让其与普通种群的染色体进行信息交流,同时在淘汰染色体重复种群过程中增加淘汰的数量,增加种群的多样性.通过锦标赛选择让染色体不过于单一也保证种群的多样性,使用文献[12]中提出的IPOX交叉来增加交叉的概率保证了遗传算法的搜索能力.同时加入了50个PSO的种群进行搜索,来增加算法收敛速度.在淘汰染色体相同的个体后,根据全局最优的染色体中获取更新机器选择的知识,使用机器选择知识来生成新的染色体以补齐两种群中个体的数量,算法流程如图7所示.
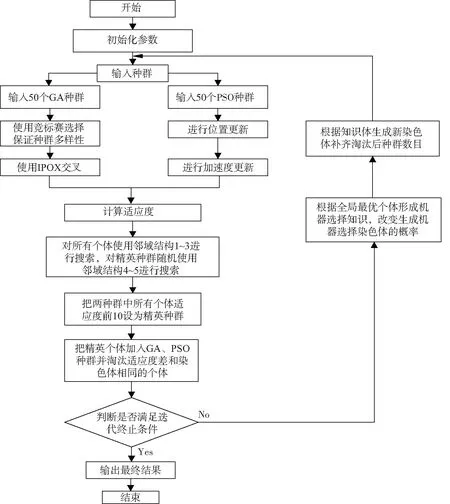
图7 学习型协同进化算法流程图Fig.7 Flowchart of Learning co-evolutionary algorithm
3 仿真与分析
本文采用MATLAB2020b进行编程并在 Windows10, Intel (R) Core (TM) i7-5500U, CPU2.4 GHz,内存4GB,输入种群规模为100,最大迭代次数为200,交叉概率为0.6,变异概率为0.1.
3.1 实验1
为了验证该算法的搜索能力,结合Benchmark标准算例,每个算例分别运行5次取最优结果为值,并找到相同参数下的不同或理论相似的算法:姜天华[6,13]于2018年提出的灰狼优化算法 (grey wolf optimization, GWO) 以及混合灰狼优化算法 (hybrid grey wolf optimization, HGWO),Caldeira 等[14]于2019年提出的改进Jaya算法(improver jaya algorithm, IJaya),Chen等[15]于2020年提出的一种基于强化学习的自学习遗传算法 (self leaning Genetic Algorithm,SLGA), Ding等[16]于2020年提出的基于改进粒子群优化算法的柔性作业车间调度新编码和解码方案(improve Particle swarm optimization,IPSO)进行比较.
由表1可以看出在Benchmark算例中本文算法除了MK01~MK06、MK08~MK10算例外都可以求出与这些算法对比下的最优解;在MK06、MK07算例中,算法效果也仅比IJaya算法效果差,并且结果都是接近于最优解并且优于其他算法最优解的.同时在空间度较为复杂的大算例MK09、MK10中,在之前算例中出众的IJava、SLGA等算法无法求解或求解效果较差,但是本文算法能够求出远优于其他算法的结果.
图8为表1中标准算例MK09的调度甘特图.

表1 算例对比
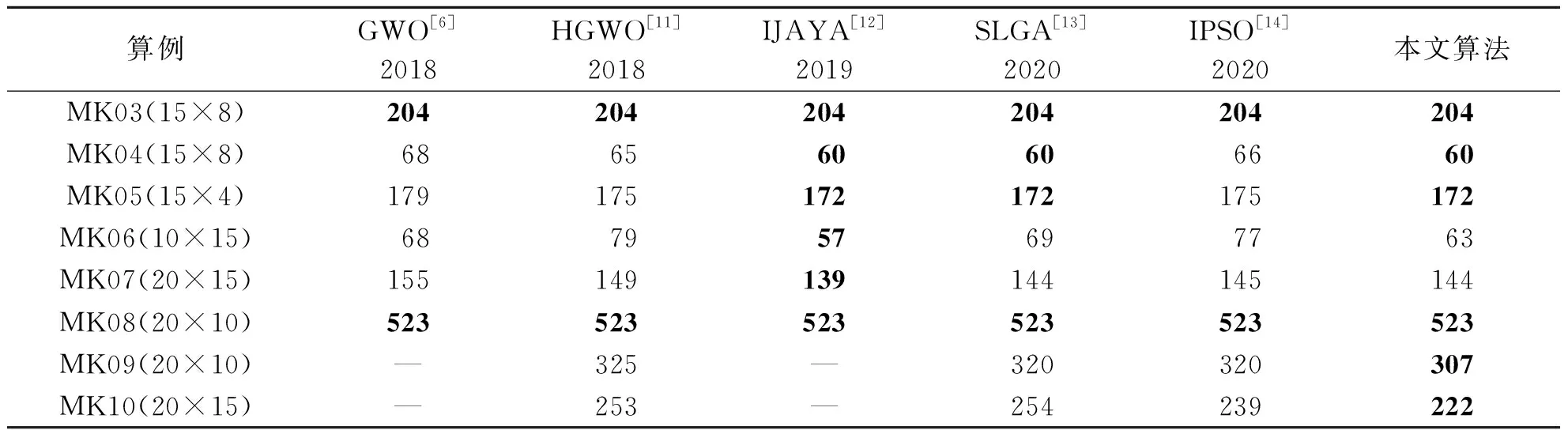
续表1
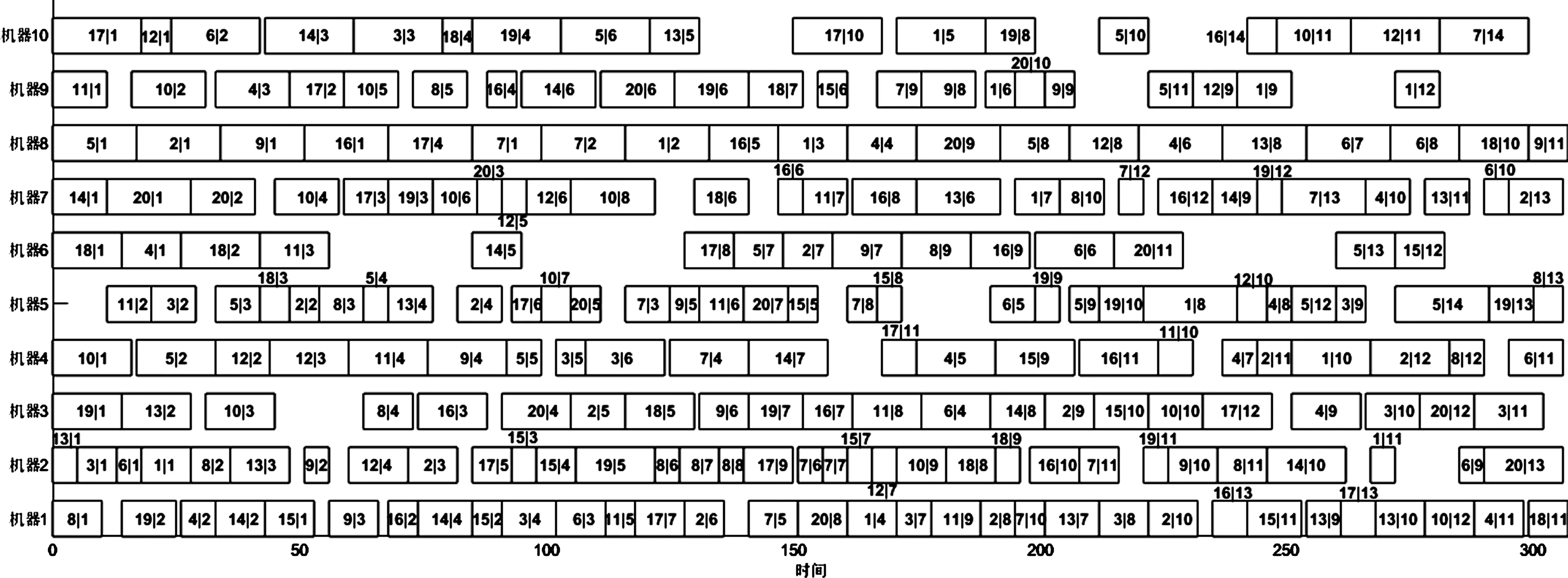
图8 MK09甘特图Fig.8 MK09 Gantt Chart
为进一步测试本文算法的优越性,将本文算法与文献[13,18,19]的算法使用kacem算例进行对比,能够求解的最优值如表2所示.

表2 算例对比
由表2可以看出本文算法在5个算例中均能求出最优值,结合表1的数据对比可以看出本文算法在求解FJSP问题时具有一定的有效性.
3.2 实验2
为了证明算法的稳定性,使用文献[16]提出的算例,同时与文献[7,15,17]的实验在相同的参数条件下进行对比求解10次并求平均值.由表3可以看出本文算法求出该算例的最优值且平均在19.3代以内就可以求解出最优值.

表3 算例对比
图9为实验2中算例的调度甘特图.
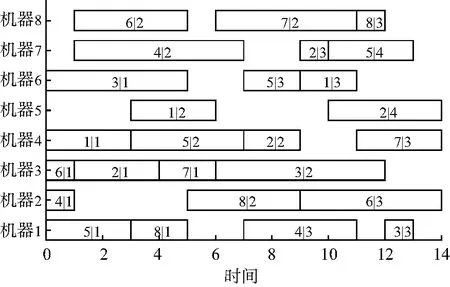
图9 调度甘特图Fig.9 Schedule a Gantt chart
可以由上面的表格数据看出本文提出的算法不仅在平均值上优于其他算法,而且稳定性方面同样表现优秀.
4 结 论
针对FJSP算法在大规模算例中搜索能力差、容易陷入局部最优解的问题设计了一套基于GA和PSO的改进协同进化算法,加入了变邻域搜索和对机器知识的学习,通过与其他算法在标准算例中的对比得出如下结论:
1) 针对最优全局个体的染色体来设计针对机器选择知识的知识体,从而影响下一代个体的生成,可以提高新生成种群的质量,提高算法的搜索能力.
2) 多种群的协同可使两算法相互竞争、共享精英个体,同时增加种群的多样性来摆脱局部最优,提高算法搜索能力.
3) 针对精英个体进行变邻域搜索,在提高算法搜索能力的同时还可以节省算法的计算工作量.

