基于融合模型的无人仓自动补货策略
方 璟 徐 明 万家乐 胡欢
(国网电力科学研究院武汉南瑞有限责任公司 武汉 430074)
0 引 言
对于国网智慧仓储建设示范项目无人值守型专业仓而言,维持充足的备品备件库存是保证应急事件处理和电力设备抢修速度的必要条件,另一方面,过量的备品备件库存不仅会占用大量资金,还会对备品备件实际使用寿命造成一定损害[1].
补货策略的核心是基于历史及现时数据,获取精准预测未来需求量的模型和方法[2].逯曼皎等[3]提出根据输出的补货矩阵表动态调整补货周期.黄国兴等[4-5]将随机森林用于需求量预测.罗薇等[6]以服务响应时间为约束条件,以库存成本及缺货成本最小化为目标建立备件两级库存决策模型.Yoo等[7-10]分别将ARIMA、LSTM、LightGBM、XGBoost等模型用于补货量预测,在某些方面表现出良好特性.
当前,仓储管理系统通常使用的补货方法主要库存警戒线法、平均消耗量法和同期消耗对比法三种.依据“库存警戒线”的库存补充方法并没有脱离人为因素的影响,仓储业务人员凭借经验和直觉设定库存的合理数量(上限、下限等)的方式并不科学,没有体现出仓储系统数字化管理的价值.“平均消耗量法”的核心在于时间区间划分,通常会利用目标控制天数(如某类物资的订货周期)来计算物资的平均消耗量,但此方法仅适用于消耗量波动不大的物资.“同期消耗量对比法”无法准确预测出各类物资受气候等因素引发的突发需求,还需要补货业务管理人员对特定情况或应急时间具有丰富的专业知识和经验.
文中基于多种物资用量模型的无人值守型电力专业仓自动补货调度策略,进一步优化备品备件等物资补充方案.
1 基于融合模型的补货策略
构建专业仓物资数量的融合模型,形成无人值守型电力专业仓的自动补货策略,用于支持仓储物资的补货流程运转,见图1.

图1 基于融合模型的补货策略
自动补货策略用于对智慧仓储的物资补充进行管理.根据仓储系统提供的物资历史申领数据、出入库记录、物资基础数据、气象环境数据、实时事件数据以及设置的相关调节参数等,通过运用合理的数学公式及融合模型自动分析和预测各类物资未来的消耗量,并表示为可供参考的物资消耗趋势,对无人值守型电力专业仓的各类物资库存量进行预警,生成合理的补货方案(含补货周期、补货量等参数),同时,也支持仓储管理系统的业务人员基于专业知识和处理经验对例外情况进行方案修订.由此,通过科学合理的补货方案来节省人力资源,加快仓储物资的周转来提高物资利用率、减少库存备品备件积压或短缺状况.
1.1 物资分类
电力专业仓存放多种类的备品备件,可以通过仓储管理系统提取各类物资的出入库记录进行大数据分析,计算各种物资的出库(领用/消耗)量波动特征(波动变化量占平均每次出库量的百分比),并采用聚类算法,根据波动特征对仓内备品备件进行类型划分,确定需求平稳(需求波动率小于等于20%)、需求波动较大(波动率大于20%)物资.
本文采用融合模型计算物资补货量,对于大多数需求平稳的物资,加大其中物资需求预测模型的权值;对于少数需求波动较大的物资,加大库存限值模型的权值.
1.2 物资需求预测模型
1.2.1模型构建
通用逼近定理(universal approximation theorem, UAT)指出,具有单个隐藏层的前馈网络(加合适的非线性单元),在包含有限数量的神经元情况下,可以逼近原空间区间内的任意连续函数.BP神经网络具有任意复杂的模式分类能力和优良的多维函数映射能力,从结构上讲,BP网络具有输入层、隐藏层和输出层;其算法本质是以网络误差平方为目标函数、采用梯度下降法来计算目标函数的最小值.
通过对已掌握的无人值守型电力专业仓数据的筛选和特征提取,以及物资需求预测课题的调研,本文构建三层BP网络结构作为预测模型的基础,采用tanh函数作为激活函数,以备件物资需求预测量为输出,迭代过程中根据BP网络结构输出值与预期值之间的差值,动态调整网络的权值.
1.2.2算法步骤
GM(1, 1)算法应用分为以下步骤.
步骤1构造序列 将BP网络的预测误差作为灰色关联预测模型GM(1, 1)的原始序列,得到
x(0)=(x(0)(1),x(0)(2),…,x(0)(n))
(1)
进而得到累加数据
(2)
步骤2级比值计算 计算原始数据的级比值
(3)
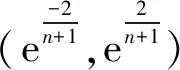
步骤3构建GM(1, 1)并计算预测值.
(4)
使用回归分析求出a、b估计值,得到白化模型.
(5)
推得
(6)
从而得到预测值.
(7)
进而得到原始数据对应的预测值.
(8)
由式(8),易得到基于预测模型的计划补货量.
(9)
步骤4相对误差计算
(10)
根据式(10)计算相对误差,相对误差值越小越好,如小于20%则说明模型拟合良好.
步骤5后验差比检验 后验差比值C为残差方差与数据方差的比值,用于衡量模型的拟合精度情况,如后验差比C值越小代表拟合效果越好,一般应小于0.65.
步骤6模型残差检验 模型残差检验为事后检验,主要用来计算相对误差值和级比偏差值.级比偏差值也用于衡量拟合情况和实际情况的偏差,一般该值小于0.2即可.
1.3 物资库存限值模型
1.3.1库存下限的计算
根据某类备件物资补货提前期以及历史统计数据,利用安全库存计算公式计算其库存量下限.
(11)
式中:dQoS为—定服务水平下的库存安全系数;σdailydemand该物资日需求量的标准差数值;Tlead为补货提前期天数.
表1为 不同服务水平(QoS)对应的库存安全系数.
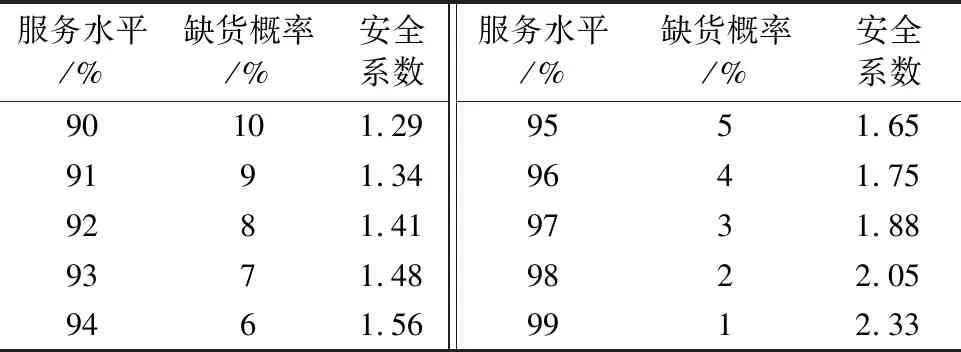
表1 不同服务水平(QoS)对应的库存安全系数
1.3.2补货周期的计算
对于某类备件物资,可以依据单次补货成本、单位物资存储成本、年需求量等参数来计算该物资平均订货周期
(12)
式中:corder为单次订货成本;cstorage为单位物资的年存储成本;D为该物资的年需求量.
1.3.3库存上限的计算
补货策略的物资库存量上限是以满足补货周期加补货提前期时段内的物资需求量为标准的,通过式(13)计算物资库存量上限.
Iupper=(Torder+Tlead)×Rdemand+Ilower
(13)
式中:Torder为补货周期的天数;Tlead为补货提前期的天数;Rdemand为物资日均需求量;Ilower为物资库存量下限.
1.3.4补货量的计算
确定好某类备件物资的库存限值后,进一步根据其当前的库存量来确定补货量,此时须考虑在途到货量和待出库数量,得到该物资的基于库存限值模型的计划补货量
Qthreshold=k×Ilower-Vtransit-Vnow+Vout
(14)
式中:k为调节系数(初始值设为2);Ilower为物资的库存下限;Vtransit为物资的在途量;Vnow为物资的当前库存量;Vout为物资当前(补货时刻)的待出库量.
1.4 融合补货方案
根据式(9)及式(14)计算得到基于两种模型的补货量,并进行加权处理得到最终的补货量.
Q=α×Qforecast+(1-α)×Qthreshold
(15)
对于某一类物资,可经过反复测算得到合适的α值,将补货量Q与该类物资的最小的补货批量进行比较,当补货量Q大于最小批量时,按补货量Q采购;当补货量Q小于最小批量时,按最小批量采购.
2 实验及分析
2.1 物资需求预测
采用交叉验证,将BP网络输入层、隐含层、输入层神经元数量分别设为四个、九个和一个,选用tanh函数作为激活函数,需求预测平均误差较小.物资需求的实际值和BP预测值比较见图2和表2.

图2 利用BP网络预测需求量

表2 BP网络需求预测误差
由表2可知:BP网络模型预测值与物资真实值的平均相对误差为13.397 2%.,将BP网络的预测误差作为灰色关联预测模型GM(1,1)的原始序列,根据式(3)计算得原始数据的级比值,见表3.
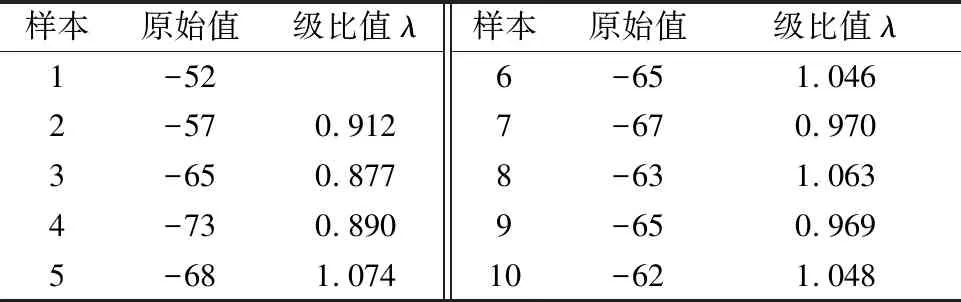
表3 GM(1, 1)模型级比值
发展系数a为0.000 2,灰色作用量b为-65.085 1,后验差比C值为0.503 1,小误差概率ρ值为0.800 0.
GM(1, 1)模型误差和物资需求真实值与预测值比较见表4~5.
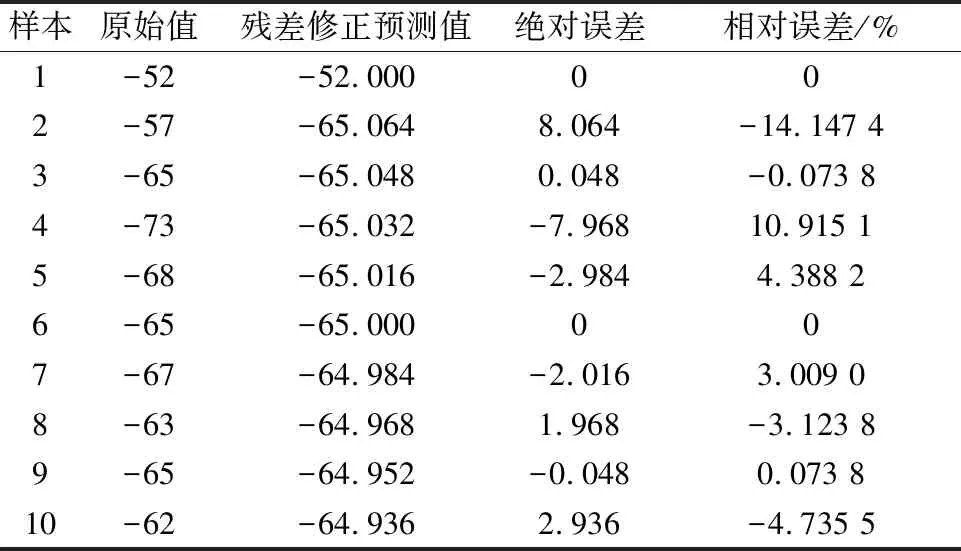
表4 GM(1,1)模型误差
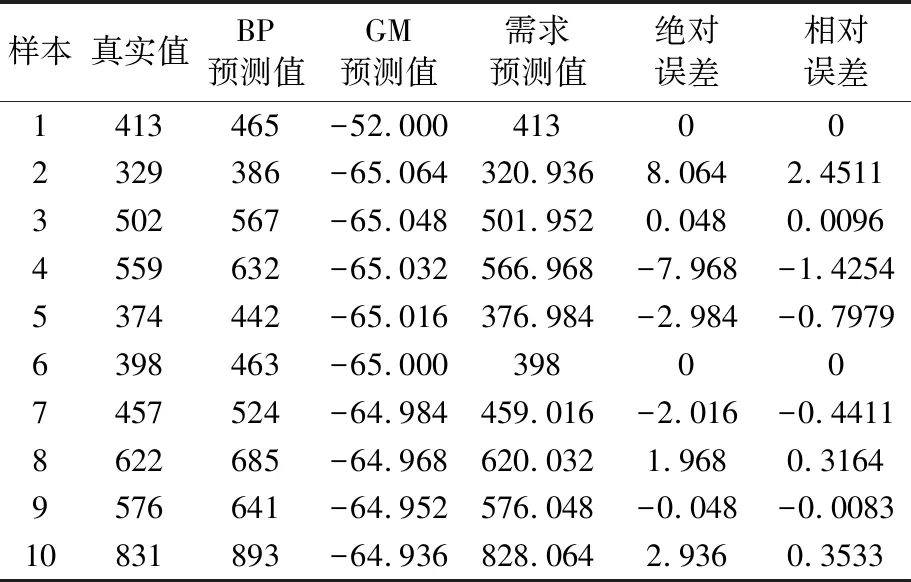
表5 物资需求真实值与预测值比较
由表5可知:经过BP网络和GM(1,1)模型处理,最终物资需求预测值与真实值的相对误差最大值为2.451 1%,优于仅用BP网络求得需求预测值与真实值的平均相对误差13.397 2%.
2.2 库存成本及周转率
提取基于仓储业务经验的库存警戒法补货方案的相关数据,依据无人仓基础参数的设置,与采用基于融合模型的补货方案进行实验比较,从库存管理成本和周转率观察两种补货方案的效能.
在某物资的补货方案中,一个观测周期内的库存管理总成本
ctotal=n×corder+Q×cunit+
(16)
而该观测周期内的库存周转率
(17)
上述各式中n为观测周期内该物资的补货次数;corder为单次补货的开销;Q为补货数量;cunit为该物资的单位价格;Vstart和Vend分别为该物资观测周期起始时刻和结止时刻的库存量,而cstorage为该物资的单位存储成本,假设corder=10×cunit,cunit=10×cstorage.
图3为本文方案与传统补货方案库存管理总成本和周转率比较,本文方案相较传统库存警戒方案,库存管理总成本至少下降6.09%,库存周转率至少提高28.54%.
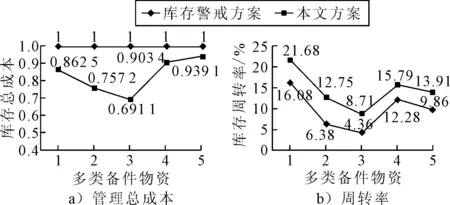
图3
3 结 束 语
针对无人值守型电力智慧专业仓的实际情况,文中提出了自动补货策略实现各类物资备件的库存控制,提升了整体运营的质量.其中,利用聚类算法根据物资需求的波动性进行物资分类,基于物资历史申领数据、出入库记录、物资基础数据、气象环境数据、实时事件数据等通过融合模型获得补货方案,给出各类备品备件的具体补货周期、数量等详细信息,在降低运行成本的同时大大提高了智慧仓储的作业效率.实验结果表明,基于融合模型的补货策略在库存总成本、库存周转率指标比较中均优于基于库存警戒法的补货策略.

