永磁同步直线电机磁阻力优化设计

许孔孔,贾 萍，尹海韬，刘云涛

(西安航天动力测控技术研究所，西安 710025)

0 引 言

在直线传动系统中，直线电机将旋转电机的旋转运动转变为直线运动，消除了中间传动环节的传动损耗而受到广泛应用[1]。然而永磁直线电机存在的最大的问题就是推力波动大，容易造成机械振动和噪声，影响直线电机的稳态性能。直线电机的磁阻力(Detent Force DF)是造成直线电机推力波动的重要因素之一，磁阻力主要包括两个分量，一是由于直线电机两端开断引起的端部力，二是初级开槽导致的齿槽力，减小磁阻力就是减小这两个分量。在减小端部力方面，文献[2]在得到最优初级长度的基础上，采用分磁环理论，在直线电机端部通过贴磁块来减小端部力。文献[3]采用增加辅助极的方法削弱端部力，并采用侧向力的方法推导出了辅助极的位置和结构参数。文献[4]在基于麦克斯韦理论基础上，对单电机和基于相叠加原理的多电机结构进行优化，削弱了端部力。文献[9]进行了直线电机的结构优化，可以同时利用三台功能相同的直线电机的绕组换位来消除电流不对称的现象，从而降低了直线电机的纵向波动力；在减小齿槽力方面，大多采用增加辅助槽，优化齿槽结构参数以及选择合适的槽极配合的方法减小齿槽力[6]。

前人的研究大多是通过优化齿槽或端部的结构参数进行磁阻力的削弱，通过降低磁阻力的谐波进而减少磁阻力的研究相对较少。本文在前人研究工作的基础上，基于傅里叶级数进行直线电机齿槽力的解析推导，得出偶数槽可以抑制齿槽力偶次谐波幅值，进而削弱齿槽力的结论，并采用有限元法建立8极9槽原始模型和拆槽后的8极10槽虚拟槽模型进行验证，分析了直线电机左右端部齿相对次级的位置对磁阻力的影响，并通过优化端部齿降低了端部力，为直线电机的设计提供参考[7-13]。

1 直线电机磁阻力分析模型

推力波动一直是阻碍直线电机发展的重要原因之一，磁阻力是影响推力波动的重要因素，产生端部力的本质在于直线电机左右两端开断，端部的导磁介质发生突变，导致两端的磁场发生畸变，从而产生端部力；齿槽力显然是由开槽效应引起气隙磁密的不均匀性导致。因此削弱磁阻力的关键在于减小端部力和齿槽力。直线电机种类繁多，本文只针对长次级短初级直线电机进行分析计算。电机初始模型采用8极9槽，考虑实际工艺的实现，槽结构采用开口槽，空载下的磁阻力仅考虑纵向边端力和齿槽力，初级铁心和轴材料用10#钢，永磁体采用SmCo28，Halbach充磁方式。图1为分析模型，表1为模型的结构参数。

图1 直线电机分析模型

表1 直线电机主要参数

2 磁阻力解析式推导

磁阻力主要包含两部分分量，分别是边端效应的端部力和齿槽力，直线电机端部力可通过优化初级长度进行改善，优化后的直线电机最优初级长为383 mm，以下仿真均是在此条件下进行。

基于旋转电机理论，单个槽的齿槽力可以采用傅里叶级数展开为[10]

(1)

式中,Fn为n阶谐波的幅值，δn为n阶谐波的初始相位，x为动子位移，为极距。

若忽略齿槽边缘效应影响，可认为直线电机的齿槽力为每个不同相位的齿槽所受电磁力之和，相邻槽之间相差一个槽距为s，则第2个槽所受齿槽力为

(2)

多个槽，槽数为K，K为偶数时，由叠加原理可得：

(3)

当总槽数K为奇数时，由叠加原理可得：

(4)

由式(3)和式(4)可知，对于总槽数K为偶数时，齿槽力中所包含的低于K次的低次偶数次谐波幅值均被抵消，仅包含K及K的整数倍次谐波。对于总槽数K是奇数时，由于第K个槽的存在，直线电机齿槽力低次谐波理论上来说会增高，对直线电机的性能产生影响。因此选择合适的总槽数可减小齿槽力及齿槽力所包含的谐波。

3 磁阻力有限元验证与分析

基于以上解析计算，下面利用有限元法对8极9槽永磁直线电机的磁阻力进行优化分析， 直线电机模型为短初级长次级结构，次级作为动子，初级作为定子。

3.1 齿槽力优化分析

对于8极9槽极槽配合，下面进行磁阻力分析，根据图1模型的有限元仿真结果如图2所示。

图2 磁阻力随时间变化曲线

图3 磁阻力谐波分布

由图2可以看出，磁阻力波动很大，峰峰值为1080 N。由图3可知，磁阻力的2次，4次，6次，10次等偶次谐波幅值比较大。

根据上述结论，奇数槽直线电机由于第K个槽的影响，使磁阻力中的低次谐波不能相互抵消，如果使槽数增加到偶数槽，理论上来讲齿槽力的低次谐波会被消除，磁阻力谐波仅含有K及K的倍数次谐波分量。下面将一个完整的槽拆成两个半槽，设置在初级铁心的左右两端，拆槽后的8极9槽直线电机有限元模型如图4所示。

图4 拆槽直线电机仿真模型

由图4，从两边对称性角度出发，左右两端的槽宽设计为原来槽宽的一半，边齿宽度随最优初级长度进行设计。直线电机总槽数由9槽增加为虚拟的10槽，将K=10代入式(4)可得：

(5)

对10槽8极直线电机，有

10s=8

(6)

将式(6)代入式(5)中可得：

(7)

由式(7)可以看出，理论上齿槽力包含的2次，4次，6次谐波被抵消，只含有10次及10次以上的偶次谐波，其幅值对基波的影响很小。优化后的磁阻力及磁阻力谐波有限元仿真如图5所示。

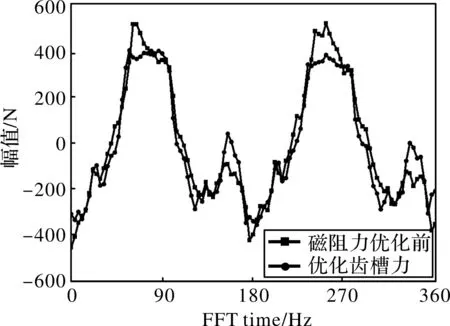
图5 优化齿槽力后磁阻力随时间变化曲线

图6 优化齿槽力后磁阻力谐波分布

由图5可以看出，相比于优化前，优化后的磁阻力为716 N，降低了33.7%，符合理论推导。由图6可以看出，与优化前相比，谐波幅值大幅度减小。验证了上述结论的正确性。

直线电机负载电磁推力的考核通过注入时间上三相对称的交流电作为激励。优化前后直线电机的负载推力如图7所示。

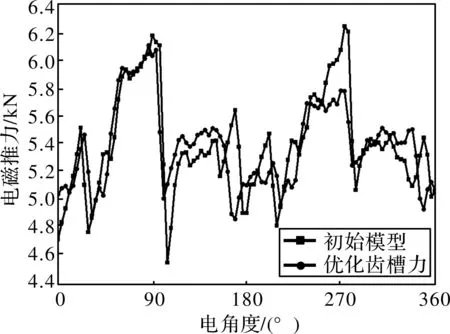
图7 优化前后负载推力

由图7可知，优化前，直线电机的负载推力波动值为1.8 kN,负载推力均值为5.4 kN,推力波动值占额定推力的33.3%，优化后，直线电机的推力波动值为1.05 kN,负载推力均值为5.34 kN,推力波动值占负载推力的19.6%，通过优化，推力波动占比减小了13.7%。验证了本文通过拆槽抑制齿槽力谐波进而减小齿槽力是可行的。

3.2 端部齿优化分析

虽然优化了直线电机的齿槽力，但负载推力波动值占推力均值的比值仍然较大，这是由于直线电机还存在幅值较大的端部力[2]。端部力是由于初级铁心两端开断，气隙磁导发生突变导致，如果直线电机的左右端部恰好运动到某一点，端部齿中磁力线不穿过气隙，与次级永磁体不构成回路，此时气隙中的磁导不会突变，端部力应最小，此时磁阻力中的主要成分是齿槽力。

分析图5发现，直线电机磁阻力曲线每一次过零时，直线电机左右端部齿均会同时处于N极，S极或辅助极，且周期循环。循环过程如表2所示。

表2 磁阻力曲线过零点端部齿位置分布

其中右端部齿位于辅助极的位置如图8所示，左端部齿与永磁体相对位置对称。此时直线电机的磁阻力曲线过第一个零点。

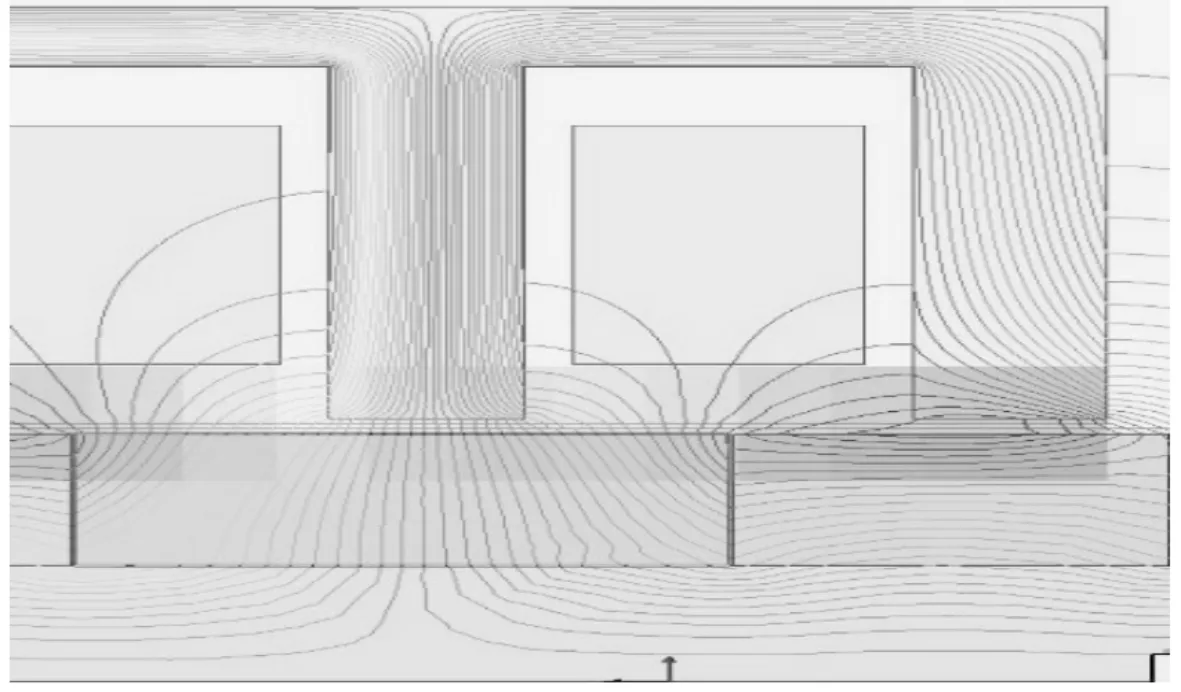
图8 右端部齿与辅助极相对位置

由图8可知，直线电机右端部齿中的磁力线基本未穿过气隙，对气隙磁场影响较小，此时磁阻力主要受齿槽力的影响。由于磁阻力此时为0，说明齿槽力对磁阻力的影响较小。

当直线电机的端部齿与次级永磁体N,S极构成回路，此时端部力最大，磁阻力也到达峰值，由此可以看出，影响磁阻力的另一个主要因素是直线电机的左右端部齿，阻断端部齿与直线电机次级永磁体的回路可抑制端部力。考虑实际工艺容易实现，采用数字化建模，分别建立不同端部齿尺寸的有限元模型，进行端部齿的结构优化，确定最优端部齿高度为21.5 mm，有限元模型如图9所示。

图9 削齿有限元模型

优化后的直线电机磁阻力波形如图10所示。

图10 磁阻力优化曲线

由图10可知，端部力优化后，磁阻力从716 N减小到380 N，降低了46.9%，优化后的直线电机的磁阻力为额定推力的7.6%，满足工程实际需要。优化后直线电机的负载电磁推力如图11所示。

图11 负载推力优化曲线

图12 负载下直线电机磁密云图

由图11可知，优化直线电机端部齿后，直线电机的推力波动幅值为0.4 kN，推力均值为5.41 kN,推力波动值占负载推力的7.4%，推力波动大幅度减小，波动范围符合实际工程要求。由图12可知，负载下直线电机初级铁心磁密均未达到饱和。优化后验证了阻断端部磁路抑制端部力是可行的。

4 结 语

本文首先从傅里叶级数角度推导了齿槽力的解析表达式，得出偶数槽可抑制低次偶次谐波幅值，进而可以削弱齿槽力的结论；建立8极9槽和拆槽变为虚拟10槽后直线电机有限元模型进行磁阻力谐波幅值的削弱，证明了解析理论的正确性；直线电机磁阻力曲线过零点与左右端部齿相对于次级永磁体的位置有关，依据此进行了端部齿的优化并降低了端部力；与优化前相比，优化后的直线电机磁阻力降低了62.9%，推力波动降低了77.1%，达到了削弱直线电机磁阻力的目的，为样机的研制提供了理论基础。