经典否定蕴涵系统定理的能行证明

杜国平

(1.中国社会科学院大学 哲学院， 北京 102488； 2.中国社会科学院 哲学研究所， 北京 100732)

经典命题逻辑有多种不同的公理系统，其中以否定和蕴涵作为初始联结词的公理系统使用最为广泛。对于这类公理系统中定理的能行证明是逻辑基础理论研究的一个重要课题，近期国内学者秦一男[1]、李晟[2]、程和祥[3-4]等都对此进行了深入探讨。受亚里士多德化归思想的启发，本文从这一视角对相关问题展开进一步探讨，给出一种新的公理系统定理证明的能行方法。

一、基元、基式

本文以如下公理系统L但不限于这一系统作为讨论的标的之一。该系统包含如下3条公理和1条推理规则：

Ax1 (B→(C→B))

Ax2 ((B→(C→D))→((B→C)→(B→D)))

Ax3 (((C)→(B))→(((C)→B)→C))

推理规则：由B和(B→C)可得出C[5]。

为了缩短公式显示长度和表达方便，下面使用在系列论文中阐述构建的括号表示法将上述公理系统重新表达[6-11]。借用括号表示法的思想，在本文的形式语言中，初始联接词符号只有一对左右括号〈 〉，两个常用的联接词符号“否定”和“蕴涵”通过以下定义引入：

(A) =def〈AA〉

[AB] =def〈A〈BB〉〉

据此，公理系统L的3条公理和1条推理规则可简化表述为：

Ax1 [B[CB]]

Ax2 [[B[CD]][[BC][BD]]]

Ax3 [[(C)(B)][[(C)B]C]]

推理规则：由B和[BC]可得出C。简记为MP。

如上所示，本文之所以使用括号表示法，一方面使用括号表示法可以精简公式，另一方面通过定义引入其他括号，既实现了对不同联接词灵活的表达，同时也不影响直观阅读[12]。

定义1.1任一大写字母A、B、C等称为基元。

定义1.2若X、Y是基元，则X、(X)称为单基式；[XY]、[X(Y)]、[(X)Y]、[(X)(Y)]、([XY])、([X(Y)])、([(X)Y])、([(X)(Y)])、[[X(Y)]([(X)Y])]和[[XY]([(X)(Y)])]称为双基式。单基式和双基式合称基式。

定义1.3对于形如[X1[X2…[XnY]…]]的公式，称X1、X2、…、Xn为其若干前件，称Y为其后件。

二、定理能行证明化归主程序

亚里士多德在其构建的三段论系统中，对作为公理之外的其他三段论形式有效性的证明采用了化归的方法，即将需要证明其有效性的三段论形式通过严格的能保持有效性的变形规则，逐步将其化归为作为公理的三段论形式[13]。受此启发，下面我们首先给出公理系统L任一定理证明的化归主程序。

下文中，以大写斜体字母X、Y、Z、M、N等以及R表述任一公式；以R{X}表述一个含有X作为子公式的公式R。

定义2.1对于主程序中的规则：

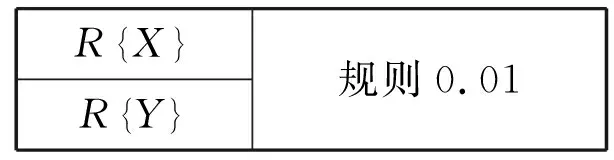
RX RY 规则0.01

R{X}称为规则0.01的输入，R{Y}称为规则0.01的输出；X称为输入的对象，Y称为输出的目标。

(一)双否消去、否定内移规则

1.双否消去规则

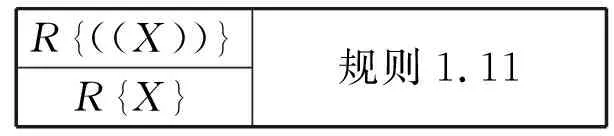
R((X)) RX 规则1.11

将公式R中形如((X))的公式替换为X。

2.否定内移规则

R ([X([YZ])]) R [[XY]([X(Z)])] 规则1.21

R ([[XY]Z]) R[[(X)Z]([YZ])] 规则1.22

理论上，还可能存在公式形如([X[YZ]])以及([([XY])Z])中的否定内移问题。但是因为：(1)单独的公式([X[YZ]])以及([([XY])Z])均不是有效式(因为如果([X[YZ]])以及([([XY])Z])是有效式，则([p[qr]])以及([([pq])r])也是有效式，而这是不可能的，如若pv=qv=rv=1，则([p[qr]])v=([([pq])r])v=0)，因此([X[YZ]])以及([([XY])Z])也不是定理；(2)([X[YZ]])以及([([XY])Z])没有比其更简单的单一公式形式。因此，对于形如([X[YZ]])以及([([XY])Z])的公式，其中的否定内移比较复杂。需要考虑其分别作为一个蕴涵式的前、后件的情况。

R[([X[YZ]])M] R [(M)[X[YZ]]] 规则1.23

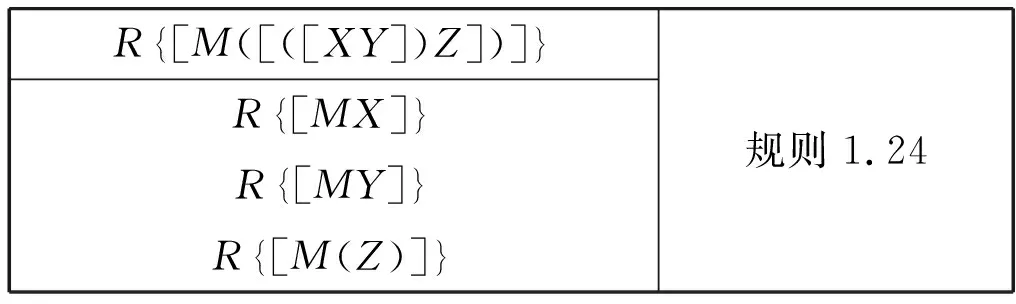
R[M([([XY])Z])] R[MX] R[MY] R[M(Z)] 规则1.24

[([([XY])Z])M] R[(M)[([XY])Z]] 规则1.25

R[M([X[YZ]])] R[MX] R[M(Y)] R[M(Z)] 规则1.26

任一公式经过对其反复使用双否消去规则、否定内移规则之后，不难发现，该公式被化归为若干个基式或者若干个其若干前件和后件均为基式的蕴涵式，简称为基蕴涵式。

(二)移动、排序规则

R[(Y)(X)] R[XY] 规则2.11

R[Y(X)] R[X(Y)] 规则2.12

R[(Y)X] R[(X)Y] 规则2.13

R[YX] R[(X)(Y)] 规则2.14

R[Y[XZ]] R[X[YZ]] 规则2.21

通过对反复使用双否消去规则、否定内移规则得到的公式再反复使用移动、排序规则可实现将其化归为将单基式移至双基式的左边，并按照字母序、肯定和否定序排列的公式。

(三)合并规则

R[X([XY])] R[X(Y)] 规则3.11

R[(X)([XY])] RX 规则3.12

R[[XY]([(X)Y])] R(Y) 规则3.21

R[[XY]([X(Y)])] RX 规则3.22

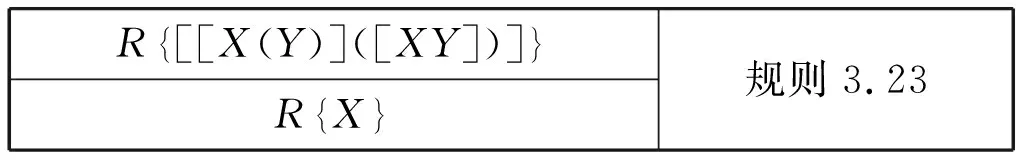
R[[X(Y)]([XY])] RX 规则3.23

R[[XY][X(Y)]] R[X(Y)] 规则3.31

R[[XY][(X)Y]] R[(X)Y] 规则3.32

R[X[Y[YZ]]] R[X[YZ]] 规则3.41

通过对反复使用双否消去规则、否定内移规则、移动、排序规则得到的公式再反复使用合并规则可实现将其化归为若干个经过简化的基式或者若干个其若干前件和后件均为基式的蕴涵式。

(四)归约规则

[X[Y[(Y)Z]]][YY]规则4.11

[X[YY]][YY]规则4.12

通过归约规则，可以将经过前述程序处理得到的公式，进一步化归为[YY]。

上述主程序中的化归规则并非都是必须的，有些可以通过其他化归规则来实现，如规则3.23可通过规则2.12和规则3.22来实现；之所以保留这些非必须的规则是为了简化化归步骤。

三、子程序

上述主程序给出了将任一公式化归为形如[YY]公式的纲要，对于其中每一个规则给出的每一步程序的具体实现还需要更加精细的子程序以实现其由公理和推理规则证明定理的具体步骤。下面不一一给出细节，只例示其中的若干子程序。

子程序5.01 ├[YY]。

证明：

1 [[Y[[XY]Y]][[Y[XY]][YY]]]Ax2

2 [Y[[XY]Y]] Ax1

3 [[Y[XY]][YY]] 1、2，MP

4 [Y[XY]] Ax1

5 [YY] 3、4，MP

子程序4.12 若├[YY]，则├[X[YY]]。

证明：

1 [YY] 子程序1.11

2 [[YY][X[YY]]] Ax1

3 [X[YY]] 1、2，MP

子程序2.21 若├[X[YZ]]，则├[Y[XZ]]。

证明：

1 [X[YZ]] 前提

2 [[X[YZ]][[XY][XZ]]] Ax2

3 [[XY][XZ]] 1、2，MP

4 [[[XY][XZ]][Y[[XY][XZ]]]] Ax1

5 [Y[[XY][XZ]]] 3、4，MP

6 [[Y[[XY][XZ]]][[Y[XY]][Y[XZ]]]] Ax2

7 [[Y[XY]][Y[XZ]]] 5、6，MP

8 [Y[XY]] Ax1

9 [Y[XZ]] 7、8，MP

子程序1.11 若├X，则├((X))。

证明：

1 [[((X))(((X)))][[((X))((X))](X)]] Ax3

2 [[[((X))(((X)))][[((X))((X))](X)]]

[(((X)))[[((X))(((X)))][[((X))((X))](X)]]]] Ax1

3 [(((X)))[[((X))(((X)))][[((X))((X))](X)]]] 1、2，MP

4 [[(((X)))[[((X))(((X)))][[((X))((X))](X)]]]-

[[(((X)))[((X))(((X)))]][(((X)))[[((X))((X))](X)]]]] Ax2

5 [[(((X)))[((X))(((X)))]][(((X)))[[((X))((X))](X)]]] 3、4，MP

6 [(((X)))[((X))(((X)))]] Ax1

7 [(((X)))[[((X))((X))](X)]] 5、6，MP

8 [[(((X)))[[((X))((X))](X)]][[(((X)))[((X))((X))]][(((X)))(X)]]] Ax2

9 [[(((X)))[((X))((X))]][(((X)))(X)]] 7、8，MP

10 [(((X)))[((X))((X))]] 子程序4.12

11 [(((X)))(X)] 9、10，MP

12X前提

13 [X[(((X)))X]] Ax1

14 [(((X)))X] 12、13，MP

15 [[(((X)))(X)][[(((X)))X]((X))]] Ax3

16 [[(((X)))X]((X))] 11、15，MP

17 ((X)) 14、16，MP

通过这些子程序将相应主程序中的每一步都落实到具体的3条公理和推理规则MP上。

四、嵌入程序

如果输入的目标就是待证明定理即主程序的输入，则直接使用子程序即可完成定理的化归与证明；如果输入的目标不是待证明定理即不是主程序的输入，而是其子公式，则需要借助嵌入程序完成将子程序楔入主程序的工作。

以主程序中的规则1.11为例，如果待证定理就是形如((X))的公式，则直接使用子程序1.11即可完成由((X))到X的化归；如果输入的目标((X))仅仅是待证定理的子公式，则需要借助嵌入程序1.11完成将子程序1.11楔入主程序的工作。

如果((X))不是待证明定理即不是主程序的输入，而仅仅是待证定理的子公式，则需要递归证明3种情况：(1)作为否定式的子公式，即主程序的输入是(((X)))；(2)作为蕴涵式前件的子公式，即主程序的输入形如[((X))Y]；(3)作为蕴涵式后件的子公式，即主程序的输入形如[Y((X))]。因此，相应地需要3个嵌入子程序。

嵌入程序1.11(1)若├(X)，则├(((X)))。

这是子程序1.11的一个特例，证明与其类似。

嵌入程序1.11(2)若├[XY]，则├[((X))Y]。

证明：

1 [[((X))[XY]][[((X))X][((X))Y]]] Ax2

2 [[[((X))[XY]][[((X))X][((X))Y]]][[XY][[((X))[XY]]

[[((X))X][((X))Y]]]]] Ax1

3 [[XY][[((X))[XY]][[((X))X][((X))Y]]]] 1、2，MP

4 [[XY][[((X))[XY]][[((X))X][((X))Y]]]]

[[[XY][((X))[XY]]][[XY][[((X))X][((X))Y]]]]] Ax2

5 [[[XY][((X))[XY]]][[XY][[((X))X][((X))Y]]]] 3、4，MP

6 [[XY][((X))[XY]]] Ax1

7 [[XY][[((X))X][((X))Y]]] 5、6，MP

8 [XY] 前提

9 [[((X))X][((X))Y]] 7、8，MP

10 [[(X)((X))][[(X)(X)]X]] Ax3

11 [[[(X)((X))][[(X)(X)]X]][((X))[[(X)((X))][[(X)(X)]X]]]] Ax1

12 [((X))[[(X)((X))][[(X)(X)]X]]] 10、11，MP

13 [[((X))[[(X)((X))][[(X)(X)]X]]][[((X))[(X)((X))]]

[((X))[[(X)(X)]X]]]] Ax2

14 [[((X))[(X)((X))]][((X))[[(X)(X)]X]]] 12、13，MP

15 [((X))[(X)((X))]] Ax1

16 [((X))[[(X)(X)]X]] 14、15，MP

17 [[((X))[[(X)(X)]X]][[((X))[(X)(X)]][((X))X]]] Ax2

18 [[((X))[(X)(X)]][((X))X]] 16、17，MP

19 [((X))[(X)(X)]] 子程序4.12

20 [((X))X] 18、19，MP

21 [((X))Y] 9、20，MP

嵌入程序1.11(3)若├[YX]，则├[Y((X))]。

类似嵌入程序1.11(2)可证。

嵌入程序1.11(1)～1.11(3)可统一表示为嵌入程序1.11。

嵌入程序1.11若├R{X}，则├R{((X))}。

类似地，对于其他主程序，除了子程序之外，也存在对应的嵌入程序。例如，对于规则2.13，有相应的子程序1.23和嵌入程序2.13。

子程序2.13若├[(X)Y]，则├[(Y)X]

嵌入程序2.13若├R{[(X)Y]}，则├R{[(Y)X]}。

对于嵌入程序2.13，同样包括3个嵌入子程序：

嵌入程序2.13(1)若├([(X)Y])，则├([(Y)X])。

嵌入程序2.13(2)若├[[(X)Y]Z]，则├[[(Y)X]Z]。

嵌入程序2.13(3)若├[Z[(X)Y]]，则├[Z[(Y)X]]。

五、能行证明程序及其示例

基于前述化归规则、子程序和嵌入程序可以给出从公理和MP规则出发的定理能行证明的基本程序：

(一)化归

1．对于任意一个待证定理Th10，交替、反复使用双否消去规则和否定内移规则，将其化归为一个基蕴涵式Th11。

2．通过反复使用移动、排序规则尽可能将Th11中有相同、相近字母的基式调整至前后相邻的位置，得到Th12。

3．使用合并规则将公式Th12化简得到Th13。

4．反复使用上述1～3步骤进行操作，直至得到可使用归约规则Th14。

5．使用归约规则将Th14化归为形如[YY]的公式。

(二)证明

对于化归进行的每一步使用子程序和嵌入程序逆向完成证明。其主要步骤如下：

1．使用子程序5.01完成证明[YY]；

2．对于通过化归而得到的Th14，则其必形如[X[Y[(Y)Z]]]或者[X[YY]]，可对其分别使用子程序4.11或者4.12完成由[YY]到[X[Y[(Y)Z]]]或者[X[YY]]的证明；

3．对于使用合并规则而得到的Th13，当其输入(输出)的对象即为输入(输出)时，使用子程序完成由Th13到Th12的证明；当其输入(输出)的对象为输入(输出)的子公式时，使用子程序和嵌入程序完成由Th13到Th12的证明。

4．对于使用移动、排序规则而得到的Th12，当其输入(输出)的对象即为输入(输出)时，使用子程序完成由Th12到Th11的证明；当其输入(输出)的对象为输入(输出)的子公式时，使用子程序和嵌入程序完成由Th12到Th11的证明。

5．对于使用双否消去规则和否定内移规则而得到的Th11，当其输入(输出)的对象即为输入(输出)时，使用子程序完成由Th11到Th10的证明；当其输入(输出)的对象为输入(输出)的子公式时，使用子程序和嵌入程序完成由Th11到Th10的证明。

我们以一些定理的证明来作为示例。

定理5.11├[[(A)A]A][14]。

首先对其进行化归：

1 [[(A)A]A]输入

2 [(A)([(A)A])] 1，规则2.14

3 [(A)(A)] 2，规则3.11

然后根据相应的子程序或嵌入程序并逆向使用化归程序完成证明，其基本步骤是：

1．使用子程序5.01证明[(A)(A)]；

2．使用子程序3.11证明[(A)([(A)A])]；

3．使用子程序2.14证明[[(A)A]A]。

为了简洁显示证明程序，先证明两个引理。在定理严格的公理证明之中，根据需要，这些证明只需适当替换即可插入到完整的证明之中，从而还原为公理证明。

引理5.01若├Y，则├[XY]。

证明：

1Y前提

2 [Y[XY]] Ax1

3 [XY] 1、2，MP

引理5.02├[((X))X]。

证明：

1 [[(X)((X))][[(X)(X)]X]] Ax3

2 [[[(X)((X))][[(X)(X)]X]][((X))[[(X)((X))][[(X)(X)]X]]]] Ax1

3 [((X))[[(X)((X))][[(X)(X)]X]]] 1、2，MP

4 [[((X))[[(X)((X))][[(X)(X)]X]]][[((X))[(X)((X))]]

[((X))[[(X)(X)]X]]]] Ax2

5 [[((X))[(X)((X))]][((X))[[(X)(X)]X]]] 3、4，MP

6 [((X))[[(X)(X)]X]] Ax1

7 [((X))[[(X)(X)]X]] 5、6，MP

8 [[((X))[[(X)(X)]X]][((X))[(X)(X)]][((X))X]]] Ax2

9 [((X))[(X)(X)]][((X))X]] 7、8，MP

10 [(X)(X)] Ax1

11 [((X))[(X)(X)]] 10，引理5.01

12 [((X))X] 9、11，MP

引理5.03若├[X[YZ]]，则├[[XY][XZ]]。

至此，可以给出定理5.11的公理证明如下：

证明：

1 [(A)(A)] 子程序5.01

2 [(([(A)A]))[(A)(A)]] 1，引理5.01

3 [(A)[(([(A)A]))(A)]] 2，子程序2.21

4 [[(([(A)A]))(A)][[(([(A)A]))A]([(A)A])]] Ax3

5 [(A)[[(([(A)A]))(A)][[(([(A)A]))A]([(A)A])]]] 4，引理5.01

6 [[(A)[(([(A)A]))(A)]][(A)[[(([(A)A]))A]([(A)A])]]] 5，引理5.03

7 [(A)[[(([(A)A]))A]([(A)A])]] 3、6，MP

8 [[(A)[(([(A)A]))A]][(A)([(A)A])]] 7，MP

9 [(([(A)A]))[(A)A]] 引理5.02

10 [(A)[(([(A)A]))A]] 9，子程序2.21

11 [(A)([(A)A])] 8、10，MP

12 [[(A)([(A)A])][[(A)[(A)A]]A]] Ax3

13 [[(A)[(A)A]]A] 11、12，MP

14 [[(A)A][[(A)[(A)A]]A]] 13，引理5.01

15 [[[(A)A][(A)[(A)A]]][[(A)A]A]] 14，引理5.03

16 [[(A)A][(A)[(A)A]]] Ax1

17 [[(A)A]A] 15、16，MP(1)对于定理[[(A)A]A]，存在更简洁的基于公理和MP规则的证明：1 [[(A)[[B(A)](A)]][[(A)[B(A)]][(A)(A)]]] Ax22 [(A)[[B(A)](A)]] Ax13 [[(A)[B(A)]][(A)(A)]] 1、2，MP4 [(A)[B(A)]] Ax15 [(A)(A)] 3、4，M6 [[(A)(A)][[(A)A]A]] Ax37 [[(A)A]A] 5、6，M这说明能行证明方法提供了一个可操作的证明方法，但未必是最简单的证明方法。

在上述公理证明中，第1步是由子程序5.01完成的，第2至11步完成的实际上是子程序3.11的一个代入，第12至17步完成的是子程序2.14的一个代入。

六、余论

子程序、嵌入程序都是定理证明程序；而化归主程序则和证明的方向相反，在完成化归之后，再完善定理证明时需要沿着化归程序逆向进行。

本文给出的是定理自动证明的程序大纲，后续还可进行具体的程序设计，进而完成基于本文思想的自动定理证明器。

如果增加构建一个辅助程序，在待证定理的证明中对已经证明的定理可以直接调用，这样可以大大简化定理的自动证明。

关于程序规则的合理性说明：对于任一给定待证的定理，通过使用双否消去规则、否定内移规则、移动排序规则、合并规则之后，必定可以等值地化归为一个形如[X[Y[(Y)Z]]]或者[X[YY]]的公式。因为若其不然，则在其等值化归为形如[X1[X2…[XnY]…]]的公式中，Xn不同于Y并且在X1、X2、…、Xn中不存在相互否定的公式，因此必定可以构造一个赋值v，使得(X1)v=(X2)v=…=(Xn)v=1，而(Y)v=0，因而[X1[X2…[XnY]…]]v=0，这与原公式是待证定理矛盾。因此，待证定理必定可以化归为一个形如[X[Y[(Y)Z]]]或者[X[YY]]的公式，进而可以进一步利用归约规则将其化归为形如[YY]的公式，并进而得到证明。

使用划归方法对系统的内定理进行能行证明，这与通常诉诸公理及变形规则之特征的能行证明方法不同，因为该方法的基本思想不受系统内具体公理和规则的限制(尽管文中为了说明方便，使用了一个具体的公理系统)(2)当然，对于不同于文中的公理系统，本文给出的证明程序需要适当调整，即只需对其中的双否消去规则、否定内移规则、移动排序规则、合并规则和归约规则给出系统内的证明子程序。而整个能行证明的主体框架和化归的基本思想是没有改变的。。所以，该方法比较而言，更具一般性，因而也更加容易推广到其他公理系统之中。