山区高填方边坡数值模拟与监测分析

卜其发

（大埔县公路事务中心,广东 梅州 514299）

0 引言

山区公路建设中的高填方路基边坡数量越来越多，高填方路基施工有助于跨越多类型复杂环境，减少公路周围生态的破坏。高填方路基填筑周期长、工程量极大，且在后续运营过程中容易受到外界环境及行车荷载影响而产生塌陷、沉降等病害。为此，开展高边坡沉降监测方案设计能够获取科学合理的变形发展规律，继而为公路维修养护提供理论指导，具有重要的社会经济意义。

1 工程概况

广东省某一级公路是衔接周围县市经济产业的重要交通渠道，设计全长25 km，设计车速80 km/h，双向四车道，设计主线跨越了大范围山区丘陵。路段K120+300～K129+450沿线植被覆盖面积大，填方路基数量多。其中，K125+200处存在中心填筑高度32 m的高路堤，右侧边坡高度24 m左右，左侧边坡高度71 m左右。路堤填筑材料主要采用路段周围大范围分布的风化素填土、土石混合材料、砌石[1]。其中，下部砌石、中部土石混合材料的稳定性、强度较高，项目组对素填土进行室内工程试验，其物理性质如表1所示。路段地基横断面向300 m范围经勘察可知地层岩性由下至上分为以下两层：粉砂岩层，中风化，稍密，含水率高，厚度30 m，重度25 kN/m3，黏聚力1 350 kPa，泊松比0.21；粉质黏土层，厚度10 m，低液限，含水量丰富，内部粉砂含量高，重度19.5 kN/m3，黏聚力29 kPa，内摩擦角22°。该高填方路堤填筑坡度1∶1.5，台阶式填筑形式，分9层填筑，由下至上分别选取砌石、土石混合材料（填料比50∶50）、风化素填土进行填筑，路堤顶部填筑宽度25 m。现场项目组为分析高填方路堤边坡施工沉降变化规律，进行现场沉降监测方案设计和有限元数值分析，以便为后续运营沉降监测及路基维护管理提供理论支撑[2]。

表1 素填土物理力学特性

2 有限元分析

2.1 模型构建

项目采用ANSYS有限元软件进行该高填方路堤边坡施工阶段沉降分析，路堤采取8级台阶式分层填筑。填筑高度32 m，1～2层采用砌石材料，3～5层采用土石混合材料，6～8层则采用素填土填筑施工。项目采用2维实体单元进行路段高填方路堤典型断面沉降分析，单位类型为8节点四边形PLANE82高阶单元，有限元模型单元划分由路堤顶部至坡脚逐渐变疏，单元数24 120个，单元节点总数7 925个。土体模型采用摩尔-库伦破坏准则[3]。有限元模型模拟材料参数如表2所示，模型构建示意图如图1所示。

图1 有限元模型构建示意图

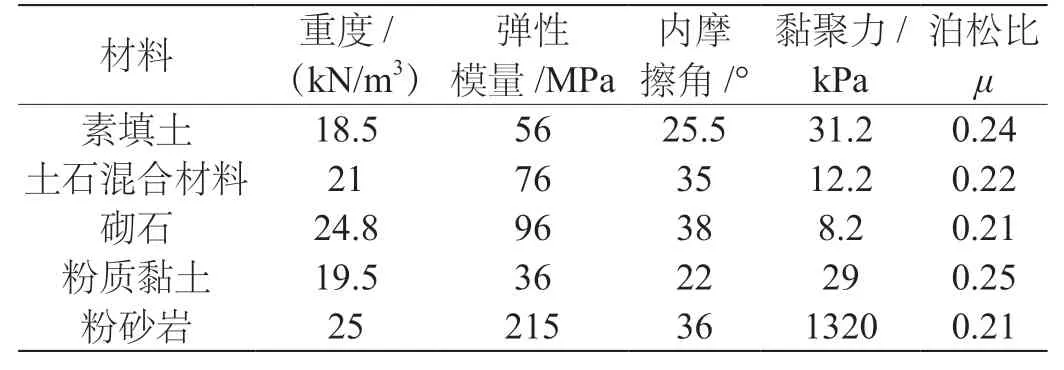
表2 模型材料参数

2.2 边界及加载

有限元模型中取X左边，Y向上方为正向，X为0、300处进行边界垂直和水平向限制。X向长度范围设定为300 m，以便充分弱化边界效应。高填方路堤总共需要8层填筑，填筑坡度1∶1.5。模拟过程如下：首先需要有限元模型自重应力场求解，进行位移清零；其次分别进行1～8级荷载施加，各级材料填筑厚度则均为4 m，分别对高边坡沉降变形发展变化值进行记录。

3 高填方边坡监测方案

路段处边坡沉降监测方案布置需要合理选取监测仪器，对施工阶段路堤进行分层沉降测定，继而进行有限元计算结果和实际监测数据的对比分析，以此评价沉降变化规律。

3.1 设备选取

路堤断面K125+200处沉降监测选取沉降管型号JTMG8600B，PVC材质，管壁厚度5 mm，外径75 mm，每一节管长度2.5 m，不同沉降管之间采取接头衔接加长处理；监测沉降管需要进行钻孔安装，孔位深度需要达到地基表面以下位置；沉降管清洁安装之后，需要在孔壁、沉降管之间进行砂料回填压实，这能够促使磁环竖向自由移动，沉降磁环需要布置在沉降管上，布置间距4 m，固定环距沉降磁环1.5 m；沉降管依照次序进行严格组装，接头处需要采用土工布进行包裹密封；设备安装结束之后，则要采用水泥砂浆进行封孔，现场做好位置标记；沉降观测阶段需要采用钢尺进行数据读取、记录，且不同读数均需要二次复读以确保其准确性，最终读数选取两次读数的平均值[4]。

3.2 监测布置

沉降管监测孔位布置在左右侧路堤路肩处，孔底深入地面以下，沉降环序号由上至下进行排列。对路堤分层填筑内部的沉降变化规律进行实测，沉降孔深度选取为15～25 m，孔径90 mm，不同监测孔位布置信息如表3所示，沉降孔布置位置示意图如图2所示[5]。

表3 沉降监测孔参数

图2 沉降孔布置位置示意图

4 结果评价

4.1 沉降监测孔监测数据

项目组进行沉降现场监测数据收集，1、2号监测孔不同磁环所监测的沉降量随时间变化规律如图3所示。其中，沉降监测始于2021年9月，截至2022年5月。监测记录数据表明，不同孔位磁环即便处在同一填筑高度也具备不同的沉降记录值，这表明沉降变形受到沉降孔位置影响较大；不同孔位沉降环沉降值随时间变化规律整体保持一致性，前期沉降发展速率变化较大，后期达到稳定状态；磁环沉降值随着磁环布置高程的增大而增大，其中高填方路堤填筑施工周期为84 d，在84 d位置处的磁环沉降发展速度产生明显变化，84 d以内的磁环沉降速度明显大于84 d之后，路堤填筑期间土体固结沉降及施工扰动造成的沉降变形速率明显要大；1、2号监测孔位的磁环1能够代表路堤顶部最大沉降值，工后沉降稳定后最大值分别为0.19 m、0.15 m。

图3 磁环沉降量时间关系曲线

4.2 计算结果分析

项目对该有限元模型进行分级加载，获取不同填筑阶段的相应孔位沉降变化值，具体如图4所示。

图4为有限元计算不同孔位磁环在不同加载工序下的沉降变化情况。其中，监测孔位1、2的磁环单元id分别为3 169，118，768，4 137，5 520；3 846，367，836，4 233。有限元分析中分级填筑最大位移发生区域主要集中在填筑施工顶部；1、2级砌石填筑产生的位移较小，这主要归因于整体厚度偏小，且地表土层受到的竖向荷载几乎没有产生一定的压缩变形，3～8级填筑过程中，随着高度的增大，路堤竖向沉降变形呈现先增大后减小的发展趋势，沉降速率最大值主要出现在5～7级填筑过程中。填方土体重量提供竖向荷载，地基承受应力随着填筑层数的增多而增大，最大沉降值计算结果主要出现在不同孔位的1号磁环，其中，1号监测孔计算最大沉降值为0.22 m，2号监测孔计算最大沉降值为0.19 m；相较于监测方案所获取的记录数据，有限元分析结果要明显偏大，但是两者沉降发展变化规律整体保持一致，计算结果也较为吻合实际发展状态，模拟计算方法具备良好的可执行性。考虑到数据对比的差异性，项目组认为具有以下几个原因：该高填方路堤在实际填筑施工阶段，不同土层的填筑材料也会产生相应的固结沉降，伴随着填筑的进行而不断完成固结。后续填筑荷载的不断增大，会导致下层土层受到的竖向应力不断增加，促使其压缩量、密实度增大，导致实际路堤整体沉降量的缩小；项目采取有限元计算方法则难以充分考虑施工过程中影响沉降的不确定因素，整体模拟过程较为理想化，土层在填筑荷载施加完成前后，则认为是处在完全固结状态，最终获取的计算数值会大于实际沉降值。除此之外，实际填筑施工中的填方材料参数（容重、弹性模量、级配等）都对其沉降速率及工后沉降值有较大影响，而模拟阶段构建的单元密度、单元类型、边界条件等也会产生沉降数据的偏差[6]。

图4 有限元计算各磁环分级加载沉降曲线

5 总结

我国山区公路建设中经常出现高填方边坡，路基高填方边坡结构能够克服局部复杂地形环境，为项目建设质量提供保障。路基高填方边坡沉降变形是边坡稳定性分析的重要内容，过大的沉降值极容易造成公路路基破坏和行车安全隐患，开展高填方边坡现场监测及数值分析能够为沉降规律预测提供必要基础。该文依托具体工程进行监测方案设计及ANSYS模拟，获取以下结论：高填方路基路肩处为最大沉降产生位置，计算模拟值相对于实际监测值要偏大，这主要受限于施工过程中较多沉降影响因素；模拟及监测沉降发展规律具有一致性，项目工后沉降满足规范要求。