客舱清洁人员调度及时间窗冲突的影响分析
曹紫萱,林宇鹏,吴植英,毛 宁,陈庆新,余龙水
(1.广东工业大学 广东省计算机集成制造系统重点实验室,广东 广州 510006;2.广东机场白云信息科技有限公司 广东 广州 510470)
随着我国航空运输业迅速发展,中国将成为民航事业中发展最快、潜力最大的国家。根据中国航空工业发展研究中心发布的《2019 ~ 2038年民用飞机中国市场预测年报》数据显示,预计到2038年中国客机规模即将达到8 678架,成为全球第二大航空市场[1]。然而,随着我国航空运输事业蓬勃发展,各航空公司飞机数量不断扩增,愈发庞大的飞机客舱清洁需求给机场客舱清洁服务人员调度工作带来巨大的挑战。目前,我国大部分机场的客舱清洁人员调度工作主要以基于经验的反应式调度为主,在航班到达雷达区域内进行清洁人员的调度。这种调度方式由于没有对整体的把控,容易造成人力资源配置不平衡,人员利用率不高,从而导致一线员工加班严重。因此对客舱清洁人员进行科学的调度,既能协助调度员进行人员安排,又能预测未来一段时间内的需求人数,有助于提高调度效率,改善人力资源安排的现状,避免员工过度加班的问题。
本文提出的问题主要与人员调度 (personal scheduling) 相关。近年来,调度问题已经被研究人员应用到不同领域,越来越多的学者也将研究目标从制造业的机器调度逐渐转移到服务行业中的人员调度。国内对人员调度的研究多集中在医护人员的调度[2-4]、多类型家庭护理人员的调度[5-7]等;国外对人员调度的研究相对较多。Van den Bergh等[8]、Aggarwal[9]分别对不同领域人员调度问题进行归纳和综述,展示了人员调度问题未来研究的研究趋势。Mason等[10]提出一种综合调度方法,使用模拟、启发式下降和整数规划技术,开发一种综合调度方法来确定奥克兰机场接近最优的人员配置水平。Zeng等[11]在经典旅行商问题的基础上,提出一种具有层次技能的新规划调度方法,即允许具有较高技能的员工覆盖较低技能的需求,并采用分支定界的方法来求解机场地勤人员的调度问题。Bechtold 等[12]对服务行业中的员工的休假问题采用不同的启发算法进行性能的对比研究。Alfares[13]在此基础上进一步进行研究和分类综述。
以上研究主要探讨员工的资质、休假等方面问题对人员调度的影响,所建立的模型都为静态调度模型,并未考虑到实际问题中的一些不确定性因素对调度的影响,比如机场客舱清洁任务的开始时间与结束时间、清洁员工的工作效率等。这些不确定性因素的存在可能导致与实际调度结果有所偏差。在调度问题中,常采用时间窗来解决各种时间上的不确定性。万铮等[14]将有时间窗和无时间窗的自适应调度算法结果与传统的平均分配型固定模板法对比,得出有时间窗的调度方法在实现价值率上比无时间窗算法有明显的提升。廖广瑞[15]研究资源存在时间窗约束的多技能项目调度问题。
本文分别采用开始时间窗和结束时间窗描述清洁任务开始时间和结束时间的不确定性,并将随机不确定的问题转化成确定性问题,建立以资源和时间窗冲突为约束,以最大化完成任务的数量和最小化任务等待服务的概率为多目标的0-1整数规划模型;提出使用任务冲突概率γ描述任务间时间窗冲突的程度。为了研究冲突概率对清洁人员调度的影响,以某机场航班数据与清洁人员的排班数据为测试算例,验证冲突概率γ对调度结果的影响及其在优化人员调度方面的指导作用。
1 数学模型构建
1.1 问题描述及假设
机场客舱清洁人员调度问题可描述为在一定调度周期内有一定数量的清洁任务,有一定数量的具有不同资质的清洁人员供调度员调度执行清洁任务;每个清洁人员可具有一种或多种资质,不同任务所需要的清洁人员的数量和资质都不同;每个任务都有一个相互独立的开始时间窗和结束时间窗;允许分配给同一清洁人员的任意两个任务时间窗之间有一定程度的重合。考虑在有限的人力资源限制和时间窗冲突约束下,如何调度清洁人员,使得被服务的任务数量最多,任务等待服务的概率最小。
为了规范和简化人员调度的过程,使得问题便于处理,并保证调度模型可以得到满意的解,通过分析和研究清洁人员的清洁流程,并结合机场实际清洁服务工作的情况,对问题作出如下假设。
1) 该调度问题是在班次型排班结果的基础上进行调度,即已知每个员工的上下班时间;
2) 将清洁人员的资质分为“新员工”和“老员工”;
3) 每个任务至少安排一名具有“老员工”资质的清洁人员;
4) 清洁人员在同一时间最多只能做一个清洁任务,且服务不能中途停止;
5) 清洁任务之间无紧前紧后的关系;
6) 员工在面临下班时间时,必须做完当前所安排的任务才可以下班;
7) 任务需要的人员均就绪后,才可以开始执行清洁任务。
1.2 参数定义
对模型中涉及的变量符号定义如表1所示。

表1 任务信息参数Table 1 Task information parameters
1.3 模型构建
1.3.1 目标函数
客舱清洁人员调度问题以最大化任务的调度数量和最小化任务等待服务的概率为优化目标。


式 (1) 表示最大化任务的完成数量。式 (2) 表示在确定这两个任务分配给同一人的情况下,使得后一个任务发生任务等待服务的概率最小。
1.3.2 约束条件
1) 服务标准约束。在客舱清洁人员的调度问题中,由于清洁任务类型、航班大小及清洁任务时长的不同,因此航空公司对不同航班清洁人数以及人员资质制定了相应的服务标准。同时在人力资源不充足的情况下,为了完成更多的清洁任务,允许减少部分任务的清洁人数,但清洁员工的数量不小于任务最低需求人数。

2) 员工资质约束。清洁任务要求新员工不能单独执行清洁任务,所有清洁任务至少有一名老员工。

3) 同一人连续做两个任务的约束。在调度过程中,如果同一个人安排了两个任务,则在这两个任务中,前一个任务的结束时间窗和后一个任务的开始时间窗之间的冲突概率要小于规定的冲突概率。

本文所建立的模型属于0-1整数规划模型,并且采用在Java中调用Gurobi求解器的方式进行求解。Gurobi为完整的LP、MIP、QP、QCQP 大规模优化器,其解决大规模问题的速度比同类优化器快,在大规模优化方面应用越来越广泛。
2 冲突概率γ与任务等待服务概率α的计算
在人力资源明显不充足的情况下,若按照任务最早可开始时间及任务最晚可结束时间进行任务指派,人力资源匹配情况如图1所示。图1为某机场一天 (从早上6:00开始到次日6:00结束) 的现有人力资源的配置情况。从图1中可以明显看出每阶段的实际工作人数不能满足该阶段内需求人数。为了在尽可能多地完成任务的同时使任务等待服务的概率尽量小,上述模型引入了时间窗、冲突概率γ以及任务等待服务的概率 α等概念,本节将对其进行详细的描述。
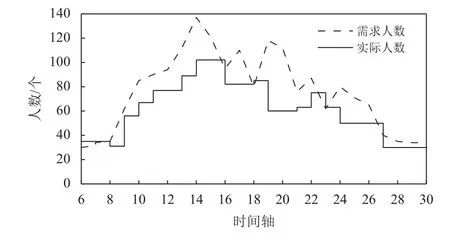
图1 人力资源负荷示例Figure 1 Example of human resource load
2.1 时间窗描述
在人员调度问题中,理想状态下,同一清洁人员的任务安排如图2所示。在任务到达后员工即可开始服务,在规定的时间内结束服务,接着下一个任务开始,立即进行服务,在规定的时间内结束,以此反复。但是在实际清洁人员调度中,任务的实际开始时间和实际结束时间都可能发生难以预测的变化。首先由于航班受天气等不确定因素影响,无法准确预知航班的到达时间,因此不能确定清洁任务的开始时间;其次由于航班脏乱程度、员工工作效率等不可控因素,无法给每个任务设置确定的清洁时长,因而无法确定清洁任务的结束时间。本文假设任务的实际开始时间和实际结束时间均服从正态分布N(μ, σ2) ,并且假设区间 ( μ-2σ , μ-2σ)为对应的时间窗,其中,均值μ、 标准差 σ根据机场客舱清洁任务的相关历史数据统计得到。开始时间窗指客舱清洁任务实际开始的时间区间,任务的实际开始时间在此区间内服从正态分布;结束时间窗则是指清洁任务实际结束的时间区间,任务的实际结束时间在此区间内也服从正态分布。图3所示为每个任务的开始时间窗和结束时间窗示例。

图2 清洁人员理想调度结果Figure 2 Ideal scheduling results of cleaning personnel

图3 实际任务的开始时间窗与结束时间窗Figure 3 Start and end time Windows of the actual task
由于相邻任务的开始时间窗与结束时间窗有可能发生重叠,那么该互相重叠的两个任务不能被分配给同一人执行,在人力资源不充足的情况下将导致某些任务无法按时完成和人员无法被充分利用。为了降低由于时间窗重叠产生的影响,允许前一个任务的结束时间窗与后一个任务的开始时间窗有一定的重合,研究不同的时间窗重合度对调度结果的影响,选择最佳的时间窗重合度,实现在一定任务冲突风险下的最佳调度方案。
2.2 冲突概率γ
上述时间窗中,当后一个任务的最晚开始时间大于或等于前一个任务的最晚结束时间时,这两个任务不发生冲突;随着后一个任务的最晚开始时间向前移动,两个任务可能发生冲突。为了描述两个任务的冲突程度,本文提出冲突概率γ。冲突概率指前一个任务的实际结束时间大于后一个任务的最晚可开始时间的概率。如图4所示,当任务1的实际结束时间发生在图中阴影面积上时,任务1与任务2将发生冲突,这两个任务原则上不能安排给同一个员工,此时阴影部分面积所占任务1结束时间窗的概率密度曲线面积即为冲突概率γ值。
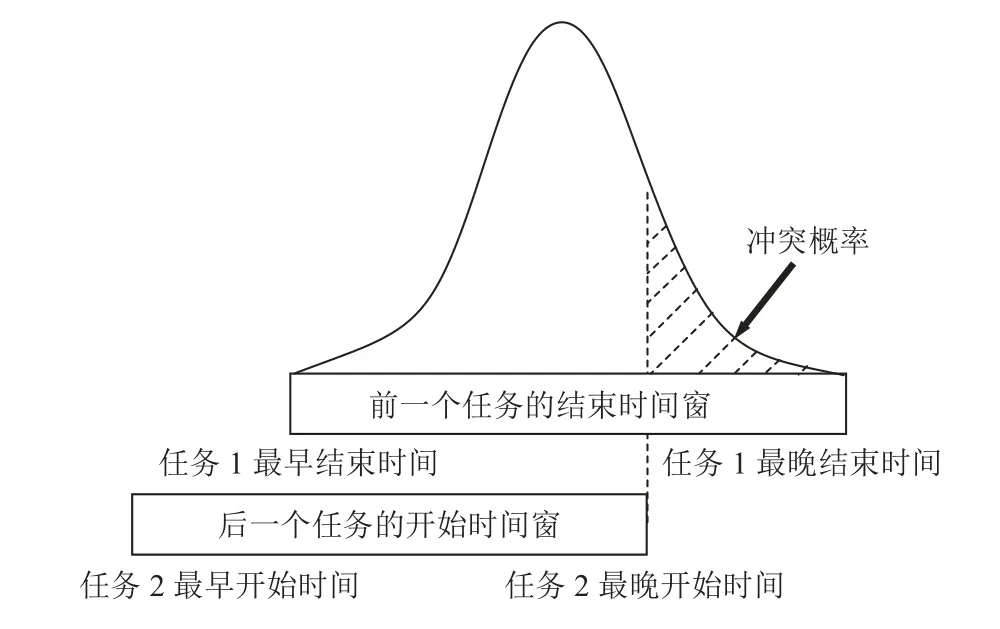
图4 冲突概率γFigure 4 The conflict probability γ
通过对历史数据的分析,可得到任务的开始时间窗和结束时间窗,虽然实际上不可能每次航班任务到达时间都在时间窗内,但是任务到达时间落在时间窗外是小概率事件。根据历史数据得到的时间窗满足正态分布的2 σ原则,任务到达发生在时间窗内的概率为95.44%。
任务之间的冲突的情况可分以下3种情况,如图5所示。其中,图5(a) 表示前一个任务的时间窗,图5(b)、(c)、(d)、(e) 表示后一个任务的不同情况。
1) 后一个任务的最晚可开始时间大于或等于前一个任务的最晚结束时间,则γ = 0。如图5(b)、(c),其中,图5(b) 为后一个任务的最晚可开始时间等于前一个任务的最晚结束时间;图5(c)为后一个任务的最晚可开始时间大于前一个任务的最晚结束时间。
2) 后一个任务的最晚开始时间小于等于前一个任务的最早结束时间,如图5(d),则γ = 1。
3) 后一个任务的最晚开始时间落在前一个任务结束时间窗内,如图5(e),则

图5 任务间冲突概率Figure 5 Probability of conflict between tasks


本文在数学模型中引入冲突概率γ的约束,是对分配给同一个员工的任务之间时间窗重合度进行约束,研究冲突概率γ对调度结果的影响,优化γ值,从而得出在一定风险下的最佳调度方案。
2.3 任务等待服务的概率α
随着时间窗重合程度的变化,人与任务之间的关系也会发生一定的变化,此时任务等待服务的情况也会越来越多,但在实际调度的过程中,要尽量避免出现任务等待服务的状况。为了方便计算,用α表示在冲突概率γ下任务等待服务的概率。



图6 任务等待服务的概率Figure 6 Probability of a task waiting for a service
3 算例分析
本节以一定时间段内某机场客舱清洁人员的实际调度工作为测试算例,在Java环境中调用Gurobi求解器求解各个γ水平约束下的数学模型,得到一定调度时段内的人员调度结果后,分析研究冲突概率γ水平对清洁人员调度结果的影响。PC配置为Intel(R) Core(TM) i5-8265U CPU @ 1.60GHz,8.0 GB RAM。
3.1 算例设计
本节以某机场客舱清洁人员调度工作为测试算例。该算例具有人力资源不足,清洁任务实际开始结束时间不确定的特点。在实际调度过程中,根据历史数据与航班计划规定每个任务的开始时间窗以及结束时间窗,并假设任务的实际开始时间和实际结束时间在时间窗范围内都服从正态分布。
在算例中将调度时段内航班任务集合 (包含任务需求的清洁人员以及开始时间窗和结束时间窗)和该时段内的清洁员工集合 (包含员工的资质以及工作时间等)作为数学模型的输入数据,以任务之间时间窗的重合程度 (γ值) 为模型的约束条件,对每个γ值水平下 (γ = 0, 0.02, ···, 0.48, 0.50) 的调度模型进行多次求解获得系统平均指标值,包括平均未完成任务数量、平均任务等待服务率、平均任务等待时长等。通过对系统平均指标值进行分析,研究冲突概率γ值对人员调度的影响。由于这些指标以及冲突概率等对调度结果具有不同程度的影响,本文提出一个评价函数,对客舱清洁人员调度的结果得出的各个参数值施加不同权重,以此为标准评价调度结果的优劣。根据多次实验结果来看,在调度过程中,未完成任务数量波动范围在0 ~ 15个之间,因此将0 ~ 15均分100分,当未完成任务数量为0时,记100分,未完成任务数量为15个时,记0分。任务等待服务所占比率为0,记100分,所占比率为1记0分。当γ = 0时两个任务之间不存在冲突,记100分,当γ = 1时完全冲突,记0分。基于文献[16]和实际调度情况,建立评价函数计算公式为

由于在调度过程中,未排班任务数量的多少以及任务冲突概率γ相对于整个调度结果的影响比较大,因此,其所占的评价系数相对较大。在提高任务完成率的基础上,适当地出现任务等待服务的情况是可以接受的,因此任务等待所占比例相对较小。调度结果的优劣,由设定的评价函数判断。评价函数值越大,调度结果越好,反之越差。
3.2 结果与分析
经过对各个γ值水平下的某机场清洁人员调度模型进行多次求解得出平均系统指标值,研究冲突概率γ对调度结果的影响。在算例中假设任务的实际开始时间和任务的实际结束时间都服从正态分布。图7为各项性能指标随γ值的变化趋势图。
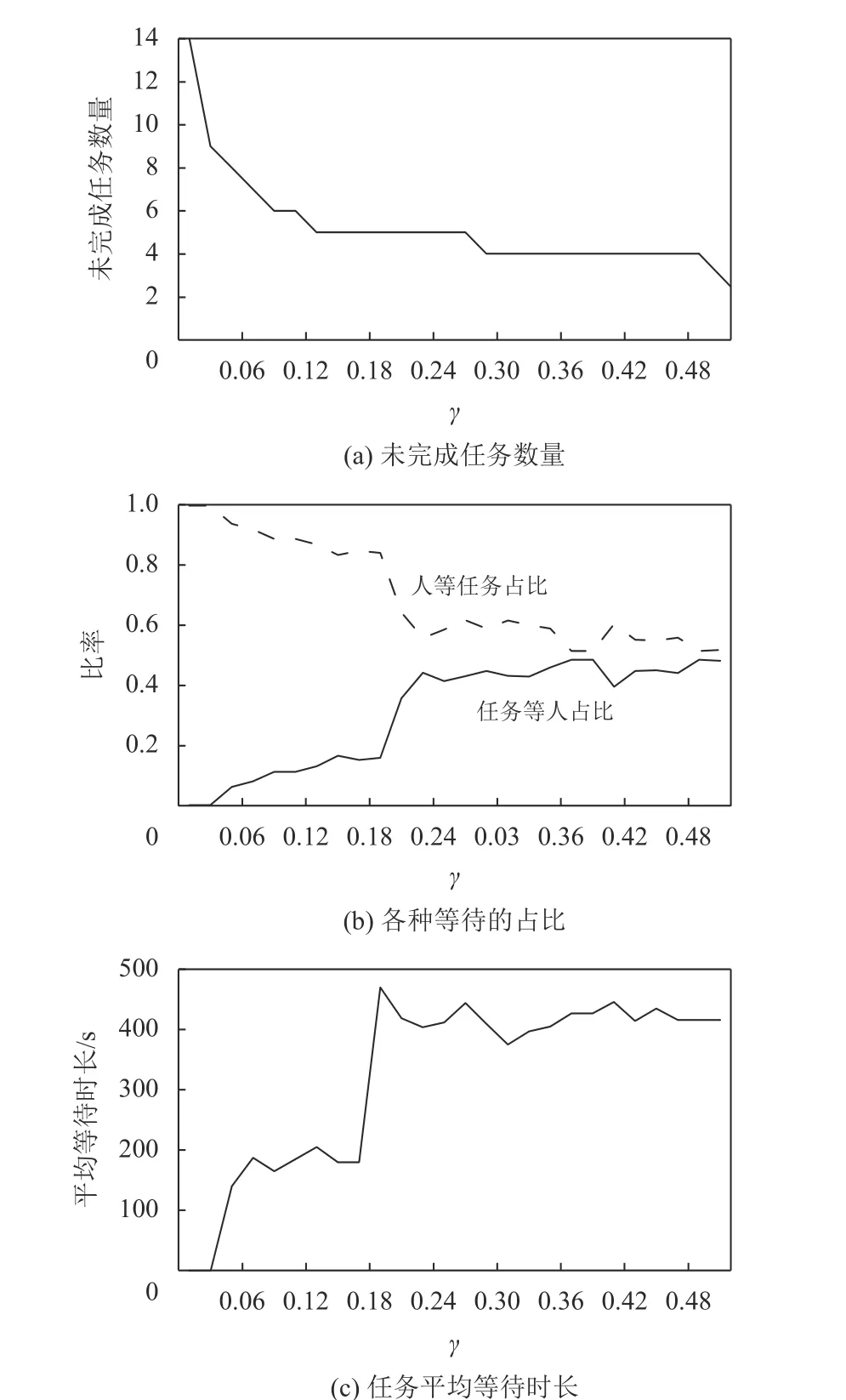
图7 系统指标随γ值的变化趋势Figure 7 The system performance in the range of γ
在图7(a) 中,当γ = 0时,时间窗不发生重合,两个任务不存在冲突,一定能安排给同一个人完成,但是未完成的任务数量较多。未完成任务是指在一定的调度周期内,在其开始时间窗内没有足够的人员提供的服务。对于未完成的任务,需要额外配置人员完成,但是这已经超出本文研究的范围,所以本文暂不对未完成任务的人员配置进行研究。当γ逐渐增大时,未完成任务数量随着冲突概率γ增大而减少,在γ ∈ [0, 0.12]区间内变化比较明显,特别是在γ = [0, 0.02]区间内未完成任务数量快速减少。而在图7(b) 中人员等待任务数占总任务的比例随冲突概率γ增大而明显减小,在γ = 0.18时变化较为明显,直到γ>0.20 时减小的趋势放缓。所以当把任务之间的冲突 (γ值) 控制在较小值时,人员等待任务的概率更大,由此容易造成人力资源的浪费和较低的任务完成率。而且两条曲线在γ = [0.20,0.50]区间内趋于平缓,这说明随着任务的冲突概率γ值的变化,任务未完成数量和人员等待任务的边际效应也在递减。因此控制调度模型中γ的值能够保证得到较好的任务完成率,有利于提高人员调度的质量和效率。
从图7(b)、(c) 可以看出,随着冲突概率γ增大,在每次调度中出现等待服务的任务占比增大,而且等待服务的时长也在增加。任务等待时长随γ值的变化总体呈现三级阶梯形状,在γ = [0, 0.06]的时候,任务发生等待服务的概率小于0.1,大多数任务基本上能得到服务;在γ = [0.06, 0.16]区间内变化平缓,在γ = [0.16, 0.22]区间内任务等人的占比明显激增,并且在γ>0.22之后呈较平稳的趋势。
随着任务间的冲突概率值γ不断增大,虽然人力资源利用率得到提高,未完成的任务不断减少,但是任务等人的概率会在一定的γ值之后急剧增大,任务等人的时长也随着加大,在实际调度过程中应尽量避免出现这种情况,因此应控制γ的范围,使调度结果在尽可能满足较高任务完成率的同时,任务的平均等待时长也尽可能降低。从图7可以看出,当把两个任务的冲突概率γ值大致控制在0.02 ~ 0.18范围内时,虽然任务等待服务占比增加,但降低了未完成任务的数量,人员等待任务占比也逐渐降低。根据式 (12) 计算评价函数所得结果如表2所示。
表2 评价函数计算表Table 2 Calculation table of evaluation function
综上分析,在人员调度模型约束条件中引入概率冲突γ值,通过将γ值控制在一定范围内,能够使任务平均等待服务时间保持较低水平的同时,保证调度结果得到较高的任务完成率。在本问题中,将γ值控制在0.02 ~ 0.18范围内,得到较高的任务完成率以及较低的任务平均等待服务时间。这为客舱清洁人员调度工作提供了实用的指导作用,具有较高的实用价值。
4 结论
带时间窗的机场客舱清洁人员调度从更贴近实际情况的角度丰富了传统的人员调度的内容。本文以某机场客舱清洁部门的实际数据为基础,以最大化任务的完成数量以及最小化任务等待服务的概率为目标,建立带时间窗的客舱清洁人员调度的优化模型。为了描述不同任务的开始时间窗与结束时间窗重叠的大小,提出冲突概率γ,并且将其引入调度模型约束条件中,研究冲突概率γ对任务调度结果的影响。以某机场清洁人员调度过程为算例,结果表明:1) 控制调度模型中的γ值能够保证得到较好的任务完成率,有利于提高人员调度的质量和效率;2) 当两个任务可能发生冲突的概率在0.02 ~0.18区间段内,得到较高的任务完成率和较低的任务等待服务概率。这在一定程度上提高了人力资源利用率,降低任务等待服务的概率,实现在一定冲突风险下的最佳调度方案。
本文构建的整数规划调度模型考虑任务实际开始、实际结束时间以及服务时长的不确定性,但未考虑人员在任务间的转移时间。在实际调度过程中,常借助摆渡车将清洁人员运送至任务地点,而由于任务到达、人员响应时间等因素,使得人员等待摆渡时间是不确定的,这将对后续清洁任务产生影响,因此人员的转移时间是调度问题中不可忽略的因素,将这一随机因素考虑进人员调度问题将是未来研究的重点。此外,本文仅考虑在人力资源配置不足的情况下,γ值对各项指标的影响,未考虑在人力资源充足情况下γ值的影响。后续工作将充分研究γ值在各种人力资源配置下对人员调度结果的影响,以及其在人力资源配置方面的指导作用。

