中国国内航空网络的分形特征研究
文 军,罗心雨,钟佳轩,徐志航
(中国民用航空飞行学院 机场工程与运输管理学院,四川 广汉 618307)
分形几何学(fractal geometry)于20世纪70年代中期由美籍数学家Benoit B. Mandelbrot提出,至今不过40余年。分形理论是在此基础上形成的研究分形性质及其应用的学科。其最基本特点是用分形维度的方法和视角对客观事物进行研究,更加符合客观事物的复杂性与多样性,更加趋近复杂系统的真实状态与真实属性。
随着学者们对复杂系统深入研究发现,大量不同拓扑结构的真实网络具有3大特征:无标度特征、小世界特征、分形特征。而在研究初期,研究人员并未意识到复杂网络会存在自相似结构,表现出分形特征。Song等[1]将重整化理论及分形理论中的盒维数法推广应用于复杂网络的研究,揭示了大量真实网络具有自相似结构,表现出分形特征,为研究复杂网络提供新角度。分形特征作为大多数复杂网络的共性这才真正被认识。张明君[2]将复杂网络的3大特征两两比较后发现,分形特征与无标度特征互相依存,分形特征与小世界特征此消彼长,分形占主导的网络更具有鲁棒性。分形维数不仅可以定量刻画网络的分形特征,同时也可用于度量分形网络的鲁棒性[3]。
航空网络是一类典型的复杂网络,其作为航空运输实现的载体,一度成为航空运输领域中热门的研究对象之一。已有文献中,对于中国航空网络拓扑特性的研究大多基于复杂网络理论。国内大量学者证实了中国国内航空网络具有小世界特性,其度分布服从双段幂律分布。牟建红等[4]基于航班时刻表,首次将时间信息引入中国航空网络拓扑结构中,实验结果与已有研究相比,其数据集中新增机场和航线使网络呈现出更加显著的无标度特性和小世界现象。杨丽等[5]对中国航空货运网络结构进行分析,证实其呈现出小世界特性,且不存在明显的社团结构。王兴隆等[6]分析结果表明,多层航线聚合网络是具有无标度特征的小世界网络。
大量的研究证实了中国航空网络的小世界特征和无标度特征,但现有文献中鲜有研究中国航空网络的分形特征,对这一特性的研究有助于深入理解网络结构的复杂性。本文首先采用复杂网络的拓扑指标对中国航空网络的基本统计特征进行描述;之后对其度度相关性进行研究,以分析网络节点间的连接偏好;最后基于分形理论,分别测算其在无权和加权条件下的分形维数,对中国航空网络的分形特性进行分析。运用分形理论研究航空网络的分形特性不仅拓宽了分形理论的应用范围,也从新的角度研究航空网络的拓扑特性,为提升航空网络的鲁棒性、抗毁性提供一种新思路,同时也为中国航空网络布局规划提供有力支撑。
1 数据与方法
1.1 航空网络拓扑建模
本文所采用数据来源于2015年和2019年夏秋国内航空公司国内航班正班计划,涉及国航、东航、南航等45家航空公司。按以下规则将数据进行简化。
1) 以通航城市作为节点,将拥有两个及以上机场的城市的数据进行合并。
2) 所统计的机场及航线数据不含港澳台地区。
3) 对有经停机场的航线进行分解,将其分解为起飞机场-经停机场和经停机场-目的机场两条航线,并将直飞航线和经停航线进行合并。
基于上述简化规则,去除各航空公司航线叠加过程中的重复项,分别构建中国航空无权网络和中国航空加权网络。其中,中国航空无权网络拓扑模型最终用一个对称无向图G=(V,E)表 示,V代表点集合,E代表边集合;中国航空加权网络以航空公司国内航班正班计划中航线一周的总航班量为边的权重,用图G′=(V,E,W)来 表示,W={w1,w2,···,wm}表示网络权重的集合。
1.2 研究方法
1.2.1 贪心着色盒覆盖算法
盒覆盖法是最早运用于欧氏空间中计算传统分形体维度的方法,该方法既能用来判断分形特征,还能求出在欧几里得空间中图形的分形维数,分形维数被用来定量表征复杂物体的特性,是对事物的粗糙度、不规则度、复杂性的一种测度。
Song等[7]在基础的盒覆盖算法上提出改进的盒子定义,即定义覆盖复杂网络节点的盒子长度lB为盒子覆盖的节点中,任意两点i、j之 间的距离dij都小于lB,对于给定盒子长度,统计出覆盖整个网络所需的最少盒子数,记为NB(l) , 其度量盒子数NB与盒子尺寸lB满足

文献[8]给出计算复杂网络的分形维数的具体算法:紧凑盒子燃烧算法、贪心着色盒覆盖算法以及最大排除质量燃烧算法。
在寻找最小盒子数时,用到了贪心着色算法,具体步骤如下。
1) 给定网络G,随机对G中节点按照1到n进 行编号;
2) 确定盒子尺寸lB大小,赋值节点1颜色值为“0”;
3) 设定lB=1, 计算di j(j<i), 即节点i和 节点j的距离;
4) 如果di j≥lB, 则选择节点j的一种颜色值赋给节点i;
5)i++, 重复步骤3)、4),直到i=n;
6)lB++, 重复2)、3)、4),直到lB大于或等于网络直径。
图1为当lB=3时的贪心着色覆盖算法示意图。
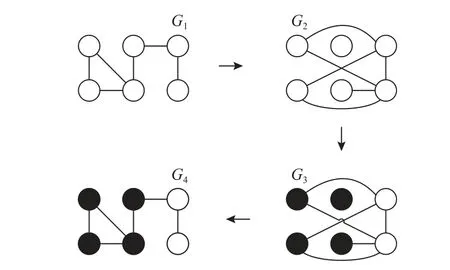
图1 lB=3时贪心着色盒覆盖法演示图Figure 1 Demonstration of greedy coloring box covering method at lB =3
Song提出的贪心着色盒覆盖算法依赖于节点的初始序列,计算过程带有随机性,只能尽可能找到最优解,且是一种穷举法,因此存在较高的复杂度。
1.2.2 无权网络盒覆盖算法
姚灿中等[9]利用Welch Powell法对文献[7]的贪心着色盒覆盖法算法进行改进,其步骤如下。
1) 将图G→G2进行交换,变换后得图G2的节点按照度序列递减次序排列;
2)G2→G3,把第1个节点放进第1个盒子,并依排列次序,将不邻接节点1的点全放进第1个盒子;
3) 在未入盒的节点中,选取度最大的节点重复2) ,处理完第2个盒子;
4) 重复3) ,直到G2所有节点全部入盒。
姚灿中等用实验结果证实了Powell改进盒覆盖算法 (box covering improved algorithm with Powell,P-BC) 的有效性,并指出该算法近似不存在随机性因素。P-BC法的实质也是贪心着色盒覆盖算法,利用Welch Powell法进行改进后能有效降低随机性和复杂度,在计算实际网络的分形维数方面具有更大的优越性。
1.2.3 加权网络盒覆盖算法
Wei等[10]摒弃了经典盒覆盖法中盒子长度为整数的想法,改变了传统盒子尺寸赋值规则中逐次加1的习惯,修正了盒覆盖法中盒子的尺度,提出了适用于加权网络的BCANw (box-covering algorithm for weighted networks,加权网络盒覆盖法) 。
具体步骤如下。
1) 计算网络中直接相连的节点间的距离值,并按从小到大的距离排序为d1,d2,···,dn;
2) 从1到n随机对节点进行编号,确定lB大小,赋值1号节点颜色为“0”;
3) 设定lB=d1, 对于i号 节点,计算节点j与节点i的 距离di j(j<i);
4) 若di j≥lB, 则选择不同于i号节点的颜色值赋给j号节点;
5)lB=d1+d2, 重复步骤3)、4),直到i=n;
6)lB=d1+d2+···+dn,重复步骤2)、3)、4),直到lB不小于网络直径;
7) 拟合l nNB~lnlB,考察其对应的直线斜率。
若加权网络具有分形特征,那么盒子长度与相应的最少盒子数目应该满足关系式

2 中国航空网络分形实证研究
分别根据2015年和2019年夏秋航季国内航空公司国内航班计划表数据,利用Gephi软件进行绘图,生成中国航空网络可视化拓扑图,如图2所示。
2015年中国航空网络由196个通航城市和1 598条边构成;2019年中国航空网络增长到229个通航城市和2 808条边。从图2中可以看出,其呈现出层级结构,且顶层结构清晰。核心层的枢纽通航城市与较多节点相连,节点度值较大,而边缘层度值则相对较小。其中,相比于2015年只有北京和上海两座通航城市节点度值大于100,至2019年,北京、西安、成都、上海、重庆、昆明、深圳、广州等主要城市节点度值已大于100,见表1。
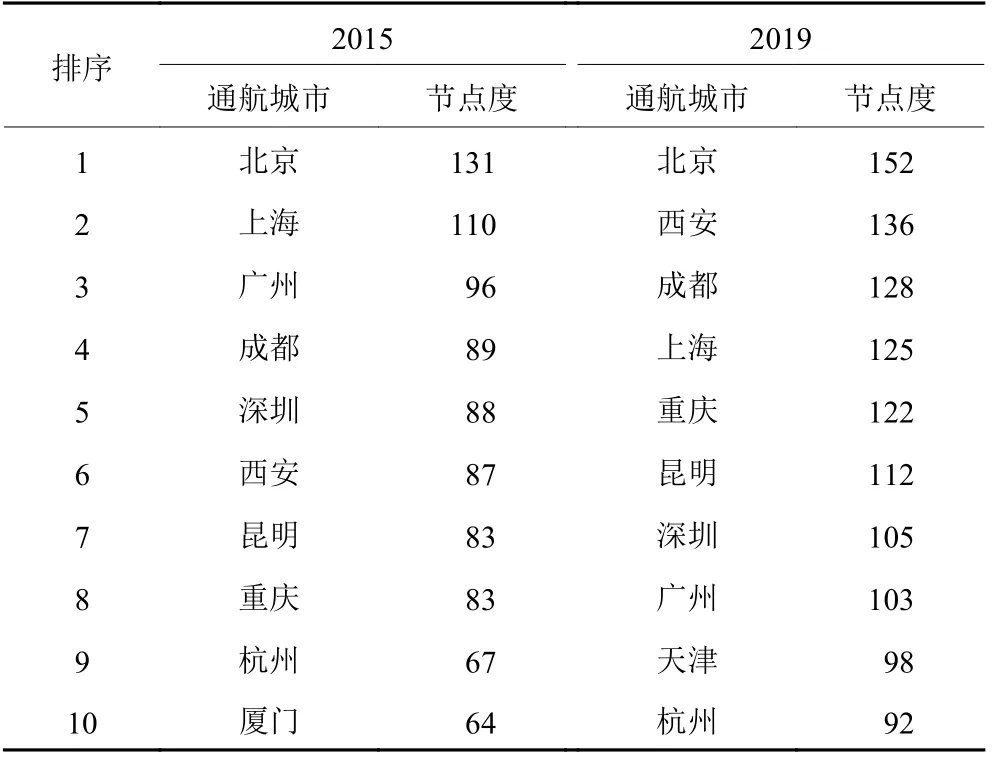
表1 中国航空网络通航城市节点度值(前10)Table 1 The node degree of navigable cities in Chinese airline network (Top 10)

图2 中国航空网络拓扑结构图Figure 2 Chinese airline network topology diagram
2.1 网络的基本统计特征
2.1.1 度及度分布
通航城市作为网络节点,其度指与该节点直接连接的边 (通航航线) 的数量。节点i的度记为

式中,ai j表 示节点i与 节点j连通情况,若节点i与 节点j之间有直飞航线,则ai j为1;反之,为0。节点度的大小与节点的重要性成正比,在航空网络中,节点度值的大小通常反映该通航城市的通达性和在整个网络中的重要性。

其中,n为网络节点数。
中国航空网络2015年和2019年的平均度分别为16.306和24.524,增长了1.504倍,即2015年平均每个通航城市约与其他16个通航城市有直接的航线连接,到2019年增长至与25个通航城市有直接的航线连接。图3、4描述了中国航空网络通航城市节点度分布及度值的概率分布,反映出中国航空网络节点度值整体上呈幂律分布。
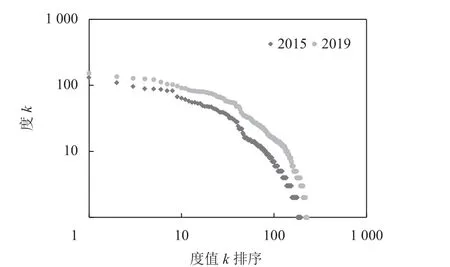
图3 节点度分布图Figure 3 Degree distribution
2.1.2 平均路径长度
将节点i和j之间的距离di j定义为连接这两个节点的最短路径上的边的数目。网络中任意两个节点(不包括自身到自身)之间距离的平均值即平均路径长度。

2015年网络的平均路径长度L1=2.202, 2019年L2=2.111,均意味着任意两个通航城市之间可通过不到2次转机就能到达。网络直径为4,即两个通航城市之间最多3次转机。网络的平均路径长度下降也表明通达性在增强。
2.1.3 聚类系数
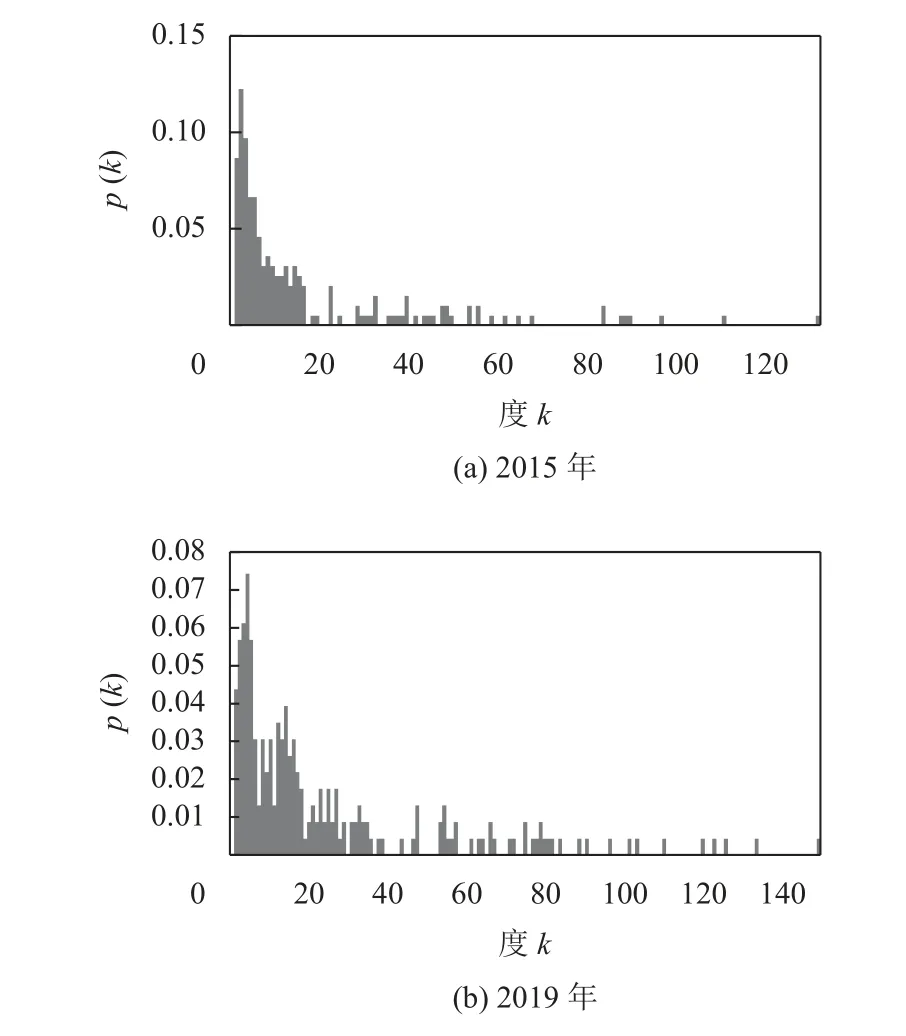
图4 中国航空网络节点度概率分布图Figure 4 Probabilistic distribution of node degree in Chinese airline network
聚类特性是大多数实际网络的共性。某个通航城市节点的聚类系数反映该通航城市与其他邻接通航城市疏密程度,平均聚类系数反映整个航空网络中所有通航城市联系的疏密程度[11]。运用Matlab计算出中国航空网络的平均聚类系数由2015年的0.753到下降至2019年的0.693,表现出很强的聚集性,聚集系数的下降则表明网络中枢层级结构在提高。中国航空网络基本统计指标见表2。
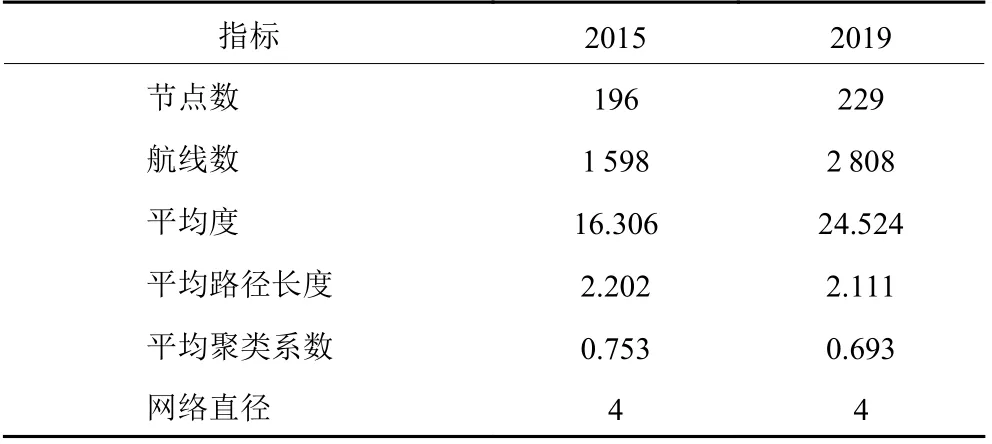
表2 中国航空网络基本统计指标Table 2 The indicators of network's basic characteristics
通过对网络基本统计特征的分析,证实了中国航空网络具有较高的聚类系数和较短的平均路径长度,同时度服从幂律分布,表明该网络具有小世界特征和无标度特征,即尽管网络本身很大,但网络中任意两节点间存在相对较短的路径。
2.2 网络的异配性分析
度度相关性是网络的一个重要统计特征,它描述了网络中节点根据度值相互选择连接的偏好特性。对于度为k的节点i与 其所有邻节近点j的邻点平均度值记为

式中,M为网络中边的数目;kz和kz′分别为第z条边两个节点的度数,z=1,···,M, -1≤r≤1。若r>0, 则节点度具有正相关性;若r<0,则节点度具有负相关性;若r=0,网络无相关性。
如图5所示,中国航空网络在2015年当k>6时和2019年当k>7时呈现明显的度负相关,以及计算出2015年和2019年中国航空网络的Pearson相关系数r均为负。这说明度大的节点偏好与度小的节点相连接,各节点的度与其所有直接联系的邻节点的平均度整体表现为负相关。节点的度值越高,其邻节点的平均度越低。随着度值的增加,这种特征表现越明显,网络为异配的。

图5 中国航空网络节点邻点平均度knn与度值k的分布关系Figure 5 Distribution of nodal knn-degree correlation in Chinese airline network
2.3 无权网络盒维数计算
本节采用Powell改进盒覆盖算法,测算中国航空无权网络G的盒维数,对其分形特征进行分析。在2.1节已计算出模型G的网络直径为4,则给定盒子尺寸lB分别为1、2、3、4对中国航空无权网络进行覆盖,运用Matlab编程计算出其对应的最小盒子数,得到一组(lB,NB)点列 ,见表3。
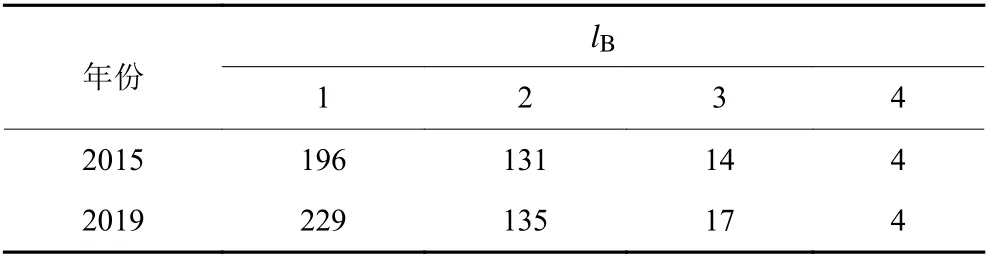
表3 中国航空无权网络覆盖最小盒子数NBTable 3 The minimum number of boxes NB in Chinese airline network without weight
对其做双自然对数图,并通过最小二乘法进行拟合,回归方程如图6所示,拟合优度R2分别为0.995 97、0.999 98,趋近1,线性关系显著,即2015年和2019年的中国航空无权网络皆具有分形特征,其分形盒维数分别为5.065、5.079。

图6 中国航空无权网络双对数坐标图Figure 6 The ln-ln plots on Chinese airline network without weight
2.4 加权网络盒维数计算
中国航空加权网络以国内航空公司国内航班正班计划中航线一周的总航班量为权重,显然,该权重为相似权,即权重值越大,距离越短,两通航城市联系越密切。定义节点i与 节点j之间的距离为

采用式 (11) 计算网络节点间距离后得到2015年和2019年的网络直径分别为0.426、0.334,均小于1。若运用P-BC法,覆盖整个网络只需要一个盒子,无法利用盒维数分析该网络的分形特征。因此,本节采用BCANw法对中国航空加权网络分形盒维数进行测算。
根据2015年和2019年中国航空加权网络的网络直径,分别给定了95和99个盒子尺寸对中国航空加权网络进行覆盖,并计算出对应的最小盒子数,将计算结果进行双对数线性回归拟合。如图7所示,拟合后得到图像在一定尺度内呈线性相关 (拟合优度R2分别为0.946 82、0.945 70,趋近1),拟合直线斜率的绝对值分别为2.164、2.262,即2015年中国航空加权网络的盒维数为2.164,2019年网络的加权盒维数为2.262,均表现出分形特征。
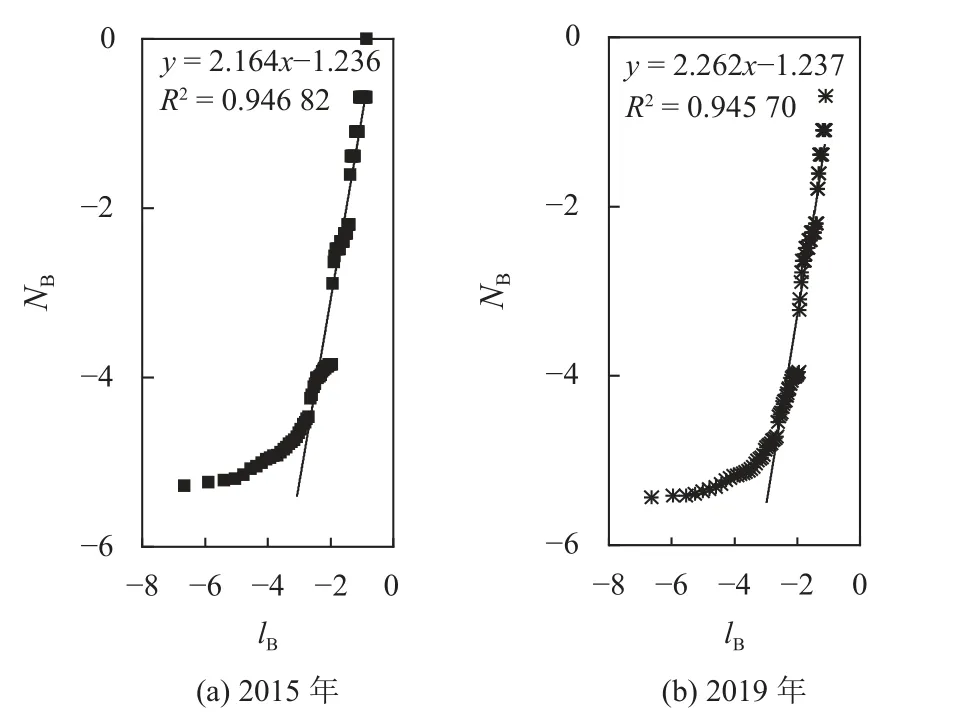
图7 中国航空加权网络双对数坐标图Figure 7 The ln-ln plots on Chinese airline network without weight
在利用盒覆盖法计算中国航空网络分形结构特征时,通航城市之间的连接深度可以通过盒子大小来体现。假设某个盒子长度中整个网络需要更多的盒子来进行覆盖,则该航空网络中通航城市间的连接关系更复杂,航空网络覆盖程度越高,其拓扑结构愈加完善,分形维数越大。
2015年至2019年,在无权和加权条件下,中国航空网络随着网络节点和航线的增加与结构的完善,分形维数呈增长趋势,其变化确切地表征了航空网络复杂度的演化与发展。
中国航空网络呈现出小世界特性,网络中两点通过尽量少的连接就能够到达,集群程度高,运输深度小,使得运输快速便捷。然而,纯粹的小世界网络由于集群点倾向于与其他的集群点相连,Hub与Hub间强烈吸引,因此在面对对Hub的目标攻击时极度脆弱,抗毁性差。分形网络集群节点则更倾向于与更少连通度的节点相连,即Hub之间连接的非同源匹配性导致了网络分形结构的产生,正是这种非同源匹配性能够增强网络的鲁棒性[15]。
3 结论
从分形视角对中国航空网络的拓扑特性进行实证研究。通过对度及度分布、平均路径长度、聚类系数的测算,验证了已有文献的结论:中国航空网络具有无标度特征和小世界特征。对网络度度相关性进行分析表明,中国航空网络为异配网络,度大的节点偏好于连接度小的节点。基于分形理论,分别在无权和以一周的航班量为权重的加权条件下对中国航空网络的盒维数进行测算。实验结果证实了在一定尺度内,中国航空网络具有分形特征,表明其具有一定的内在鲁棒性效能。网络的分形特征在2015年 ~ 2019年间演化速率虽较为缓慢,但是一种正向的演化。
本文只是对中国航空网络的分形特征进行初步分析,网络中小世界特征和分形特征谁更占主导地位,以及不同边权对中国航空加权网络分形特征的影响,仍有待于进一步的研究探索。

