基于图卷积网络的乘客打车需求预测

董成祥，魏 昕，张坤鹏，汪永超,3，杨宇辉

(1.广东工业大学 机电工程学院，广东 广州，510006；2.河南工业大学 电气工程学院，河南 郑州，450001；3.广州番禺职业技术学院 智能制造学院，广东 广州，511483)

在城市出行中，保持乘客打车需求与车辆供应之间的供需平衡是提高出行效率、缓解交通拥堵的关键。车辆共享公司 (如滴滴、优步、出租车公司等) 可以根据乘客的打车需求量，通过智能调度系统预分配车辆以有效维持乘客需求和车辆供应之间的平衡[1]。因此，准确的乘客打车需求预测是实现车辆精准调度的重要基础。然而，由于乘客打车需求的模式具有高度的非线性和动态性。在时间上，不同时间的打车需求特征不尽相同；在城市不同的区域中，乘客需求具有不同的空间特征。因此，为了准确地预测乘客打车需求，必须充分考虑城市区域间的时空特性。目前，国内外研究者对乘客打车需求的预测方法主要分为两类：传统的时间序列预测方法[2-4]和基于深度学习的时间序列预测方法[5-6]。

基于支持向量机 (support vector machine, SVM)[7]、XGBoost[8]和k最近邻 (k-nearest neighbors,k-NN)[9]等传统的时间序列方法被普遍应用于乘客需求预测。此外，Zhang等[2]运用指数加权平均移动法 (exponential weighted moving average, EWMA)建模，实现面向出租车司机的乘客需求热点预测。Moreira-Matias等[3]通过整合时变泊松 (time-varying poisson)、自回归积分滑动平均 (autoregressive integrated moving-average,ARIMA)[10]和加权时变泊松 (weighted time-varying poisson) 3种不同的时间序列分析技术预测乘客需求。Davis等[4]提出一种基于时间序列模型的多层次聚类技术预测乘客需求。然而，这些传统的时间序列预测方法并不能够充分考虑城市不同区域中复杂的时空特性。

近年来，基于深度学习的时间序列预测方法大幅提升了预测非线性、动态性问题的准确性。在捕捉时间特性方面，基于循环神经网络 (recurrent neural network, RNN)[11]的长短期记忆单元 (long short-term memory, LSTM)[12]和门控循环单元 (gated recurrent unit,GRU)[7]被广泛应用于乘客需求预测。例如，Xu等[6]以出租车历史需求为特征，运用基于LSTM的深度学习模型预测乘客打车需求。Li等[5]提出一个基于LSTM的组合模型预测多区域多时间步长的乘客打车需求。然而，尽管这些模型能够有效地从目标区域的历史观测中捕捉到乘客需求的时间特性，但他们往往忽略了区域间的空间特征。

为了将空间特征考虑在内，Zhang等[13]建立多任务学习时态卷积神经网络 (multi-task learning temporal convolutional neural network, MTL-TCNN) 模型，将不同地理区域的特征通过共享层融合在一起，实现多区域的乘客需求预测。为了同时考虑时空特性，基于卷积神经网络 (convolutional neural network, CNN)和RNN的深度学习模型被组合使用。例如，Ke等[14]将CNN和LSTM融合在一起建立融合LSTM网络(fusion LSTM network, FCL-Net) 模型预测短期乘客需求。然而，由于城市区域具有复杂的拓扑结构，基于CNN的深度学习模型不能充分抓取拓扑结构的空间特征[15]。

为了解决上述问题，本文提出基于图卷积网络(graph convolutional network, GCN)[16]的乘客需求预测模型。图卷积网络能够抓取具有拓扑结构网络的空间特性[17-19]。首先，将多区域的乘客需求特征构建为乘客需求图，在此基础上，通过GCN模块抓取乘客需求图的空间特征。其次，一个基于LSTM的编码器被用来抓取乘客需求图不同时间的时间特征。最后，一个基于LSTM的解码器被用来预测多区域的乘客打车需求。该模型的优点主要体现在：1) 基于动态时间规整算法 (dynamic time warping,DTW)算法构建的乘客需求图，能够筛选与目标区域需求模式相似的区域并与之构建乘客需求图，从而减少不相关区域对目标区域的影响；2) 在GCN模块的帮助下，能够充分抓取乘客需求图的空间特性，并且能够实现多区域乘客需求的同时预测，大幅提高预测效率；3) 基于编码-解码的模型结构，能够实现多区域乘客需求的多时间步长预测；4) 在两个不同城市的数据集上的数值实验结果验证了GCNLSTM优于主流的深度学习模型。

1 乘客打车需求预测模型建立

针对乘客打车需求预测问题建立GCN-LSTM模型，模型框架如图1所示。该模型包含4部分。首先，借助动态时间规整DTW算法将不同区域的乘客打车需求构建成乘客需求图，该部分与不同区域的乘客打车需求特征一起作为模型的输入；其次，利用图卷积网络模块提取需求图的空间特征；然后，利用基于LSTM的编码器提取时间特征；最后，采用基于LSTM的解码器实现多区域乘客需求的同时、多时间步长预测。

图1 GCN-LSTM模型框架Figure 1 The architecture of the GCN-LSTM model

1.1 问题构建

假设所研究的城市区域包含N个小区域，在过去的历史时间T中，乘客的历史打车需求变量可被描述为

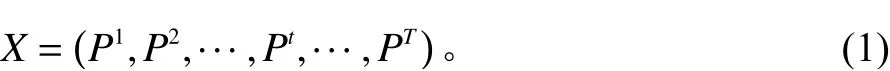
其中，Pt代 表在时间t全部区域的乘客打车需求，其表达式为

1.2 模型输入

模型的输入是图结构数据，由图G={V,E,A}表示。其中，节点V表示每个区域的乘客需求特征的集合；E表示两个节点组成的节点对之间的边的集合；A表示邻接矩阵，节点对之间的连接关系由邻接矩阵A决定。

原始数据由各区域在不同时间的乘客打车需求特征组成，其输入模型的形状为多维矩阵(B,T,F,N)。其中，B为模型训练批量大小；T为历史时间步长；F为每个区域的特征数，它由乘客打车需求数量及其对应的时间索引和周索引组成；N为研究的区域数量。

然而，当目标区域与其不相关的邻接区域构成需求图时，将会因冗余信息的引入而降低模型的预测精度。选择与目标区域时间特性相似的区域作为需求图的节点，能够减少不相关区域带来的信息冗余，从而提高模型的预测精度。乘客打车需求本质是时间序列，DTW算法能够计算两个不同时间序列的相似度。因此，引入DTW算法探究两个独立区域的乘客需求时间特性的相似性。具体来说，令xI和xII分别表示区域I和区域II在不同时间的乘客打车需求。

邻接矩阵的形状为 (N×N)， 其中N代表区域数量。该矩阵的对角线均为1，表示目标区域自身与自身相关。本文中，邻接矩阵作为输入，其形状为(B,T,N,N)。

2 图卷积神经网络模块

由乘客打车需求V和邻接矩阵A构成的图结构数据作为模型的输入，图卷积网络能够很好地从图结构数据中提取空间特征。不同于卷积神经网络仅能处理欧氏空间的数据，图神经网络能够处理拓扑结构数据。对于一个多层堆叠的图卷积网络，其层与层之间的传递方式为

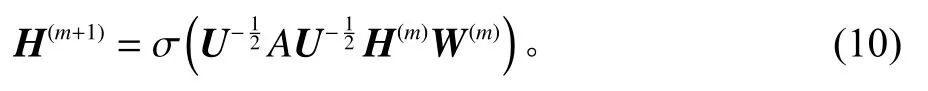
为了加速和稳定GCN-LSTM模型的训练过程，引入BatchNorm2d层对乘客需求V进行归一化处理。然后采用GCN操作对归一化的数据进行空间特性的特征提取，使输入特征转换为更高层次的特征。为了避免过拟合，在第1个GCN层之后加入了Dropout层对时间1-T的输出特征进行处理，之后再堆叠一层GCN操作对每个历史时间的输出进行更高层次的空间特征提取。为了提高上述计算过程的有效性，模型引入了残存网络结构。

3 基于LSTM的编码-解码器

乘客未来打车需求与历史需求具有时间相关性。为了抓取各区域的时间特性，编码-解码器采用长短期记忆单元 (LSTM)。LSTM单元的内部结构示意图如图2所示。

图2 LSTM单元内部结构示意图Figure 2 Inner structure of LSTM unit

LSTM单元当前输入包含3部分：当前的输入xt，前一个节点的隐层状态ht-1和前一个节点的单元状态Ct-1。当前时间的输入经过LSTM单元处理后，输出当前节点的隐层状态ht和当前节点的状态Ct。LSTM单元的关键数学表达式为

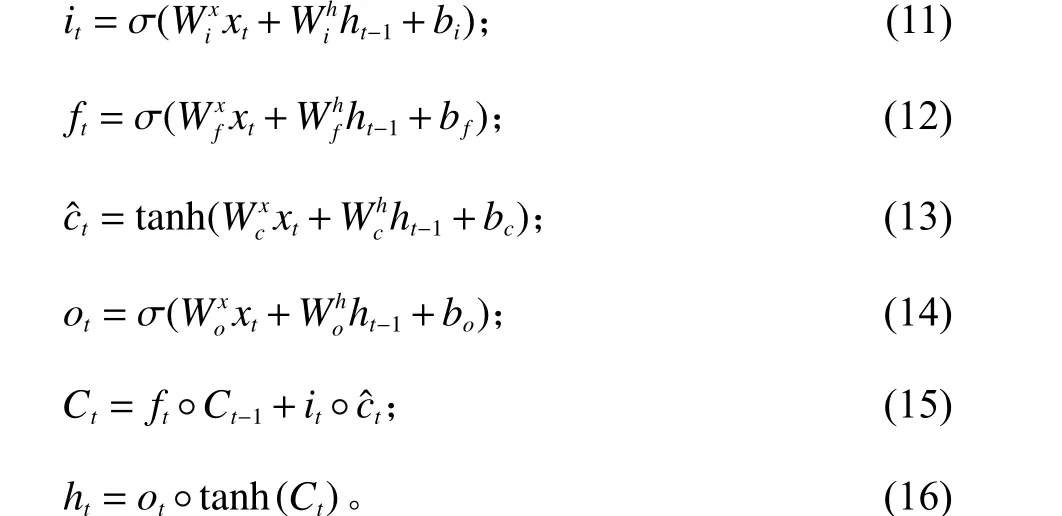
在基于LSTM的编码器中，编码器将来自GCN块的输出作为初始隐藏状态输入，将模型输入数据的最后观测值 (特征向量V的最后一个观测值)作为单元输入。经过编码器的特征压缩，编码器输出的隐藏状态作为解码器的初始隐藏状态，来自特征向量V的最后一个观测值作为初始输入，预测下一步的乘客打车需求。为了提高计算过程的有效性，在最后观测值和LSTM输出之间加入了残差网络结构，其输出经过线性变化、维度扩张操作，解码器最终输出的维度为 (B,N)， 其中，N表示预测的多区域的乘客打车需求，这大大提高了GCN-LSTM模型的计算效率。

为了实现模型的多时间步长预测，当前解码器的输出和隐藏状态作为下一个解码器的输入，可实现下一时间步长的乘客打车需求预测。重复上述过程，可实现T+s时间步长的预测。

4 实验与分析

4.1 数据集

为了验证GCN-LSTM模型的性能，选择成都市区作为研究区域，所选区域位于经度104.043°E ～104.130°E，纬度30.653°N ～ 30.726°N。该区域每天包含大约120 000个乘客叫车需求，每个请求主要包括6个参数：上车时间、上车经度、上车纬度、下车时间、下车经度和下车纬度。研究范围被划分为25个区域(5×5)，如图3所示。每个区域是一个长和宽均为1.6 km的正方形。从滴滴出行公司获取该25个区域的乘客打车需求数据集[13]，时间范围为2016年11月1日 ～ 11月30日。数据集被划分为3部分：80% 作为训练集，10% 作为验证集，其余10%作为测试集。为了获得每个区域内的乘客需求数据，求和某一时间间隔内的叫车请求数量，时间间隔设定为15 min。因此，每个区域每天产生96个数据样本。

图3 成都市的25个区域Figure 3 25 zones of study site in Chengdu

4.2 评估标准与实验条件

为了定量地评估模型的预测精度，引入均方根误差 (root mean square error，RMSE)、平均绝对百分比误差 (mean absolute percentage error，MAPE)和平均绝对误差 (mean absolute error，MAE) 对模型进行评定，表达式为

本文利用包括Scikit-learn和Pytorch在内的Python库来开发上述模型。所有数值实验均在一台配备Core i9-9920X中央处理器、16 GB内存和8 GB内存的GeForce GTX 2060S图形处理器的台式计算机上进行的。

4.3 模型预测性能对比分析

为了评估模型的预测性能，引入如下6种模型与GCN-LSTM对比。

1)k-NN。k-NN 是一种用于分类和回归的非参数方法。该算法包含4个步骤，即建立历史乘客需求数据库、定义两种交通模式之间的相似性、搜索k个最近邻并执行预测任务。

2) SVM。SVM是一种监督机器学习方法，由Vapnik等[20]首次提出。通常应用于分类、回归、信号处理等。根据结构风险最小化原则，SVM可以处理非线性和高维的问题和凸二次规划。在支持向量机中，每个区域的数据被构建为一个向量，并输入到支持向量机模型中进行训练和预测。

3) TCNN。基于卷积神经网络(CNN)，一种新的时间卷积神经网络(temporal convolutional neural networks，TCNN)被提出，借助扩张的因果卷积完成时间序列建模。在本文中，TCNN模型在不考虑空间依赖性的情况下，单独预测每个区域的乘客打车需求。训练过程中，设置训练批次大小B= 32， 历史观测时间T= 6，学习率取0.000 1。

4) LSTM。LSTM在处理时间序列的任务中表现出优异的性能，相较于RNN模型，它能够有效地避免梯度消失或爆炸问题。该模型仅考虑时间特性，并且每次只能预测一个区域的乘客需求。训练过程中，设置训练批次大小B= 32， 历史观测时间T= 6，学习率取0.000 1。

5) GRU。与LSTM类似，但比LSTM拥有更少的参数，能够提高模型的计算效率。超参数设置与LSTM相同。

6) MTL-GRU。MTL-GRU模型有25个输入(即25个研究区域)和25个输出(即这25个区域的预测值)。在该模型中，同时捕获了时间和空间特性。训练过程中，设置训练批次大小B= 32， 历史观测时间T= 6，学习率取0.000 1。

表1展示了7个模型在25个区域中预测的平均RMSE、MAPE、MAE6和预测所用的时间。可以看出，GCN-LSTM模型在RMSE、MAPE和MAE上均取得最好的结果，在预测所用时间上也明显少于其它深度学习模型(即MTL-GRU、GRU、LSTM和TCNN)。具体来讲，传统方法k-NN和SVM因为模型的计算复杂度低，预测25个区域所用时间少于深度学习模型。但是，这些传统方法因为无法考虑区域间的空间特性，且模型建模能力不足，无法提供准确的预测结果。GRU、LSTM和TCNN作为深度学习模型，相比于传统方法能够显著提高预测准确度。MTL-GRU模型在考虑交通速度的时空相关性的基础上给出了更为准确的预测结果，且用时明显少于GRU、LSTM和TCNN模型。图4显示了GCNLSTM模型在随机选取区域22的预测结果。由图4可知，预测值与真实值吻合良好，表明了预测结果的准确性。

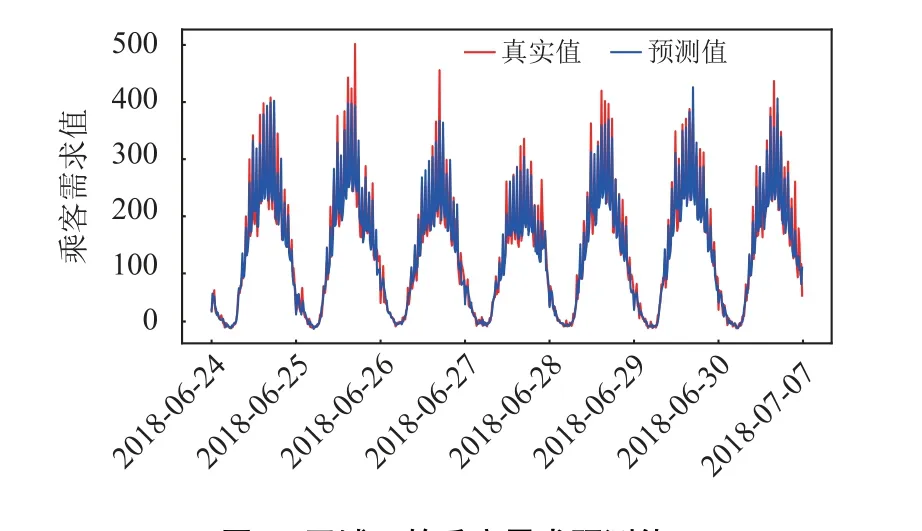
图4 区域22的乘客需求预测值Figure 4 Passenger demand values predicted for zone 22

表1 模型预测效果对比Table 1 Comparison of model prediction results

4.4 模型分析

在模型GCN-LSTM训练中，损失函数是预测值与真实值的均方误差(MSE)，优化函数是adaptive moment estimation (Adam)。学习率的取值影响模型训练过程的稳定性和效率。学习率过大，模型在训练过程中不稳定；学习率过小，会影响模型的训练效率。选取 5 种常用的学习率 (0.1、0.01、0.001、0.000 1和0.000 01)进行对比，如图5所示。随着迭代次数的增加，5种学习率对应的MSE均呈下降趋势。其中，当学习率选取0.01时，MSE波动较大，训练过程不稳定；当学习率选取0.000 1时，MSE在前20次迭代过程内迅速下降，在20 ～ 100次迭代过程内，其MSE略有下降且保持平稳。通过与其他4种学习率的对比，学习率设定为0.000 1时，模型的训练过程稳定，误差较小，且最先收敛。因此，GCN-LSTM的学习率取为0.000 1。

图5 学习率对比Figure 5 Learning Rate Comparison

选取合适的历史观测时间，对提高模型的预测精度至关重要。较短的历史观测时间，不利于模型对时间特征的提取；较长的历史观测时间，会因冗余信息的引入而降低模型预测精度。如图6所示，历史观测时间从1增加到6时，模型的预测误差RMSE逐渐降低，说明随着历史观测时间的增加，模型能够抓取到更多的时间特征，有利于模型预测精度的提高；当历史观测时间从6增加到10时，RMSE逐渐增加，说明冗余信息随着历史观测时间的增加而增多，从而降低了模型的预测精度。同时，模型的训练时间随着历史观测时间的增加而线性增加，这是由于较多的历史观测值会增加计算机的处理时间和模型的训练时间。

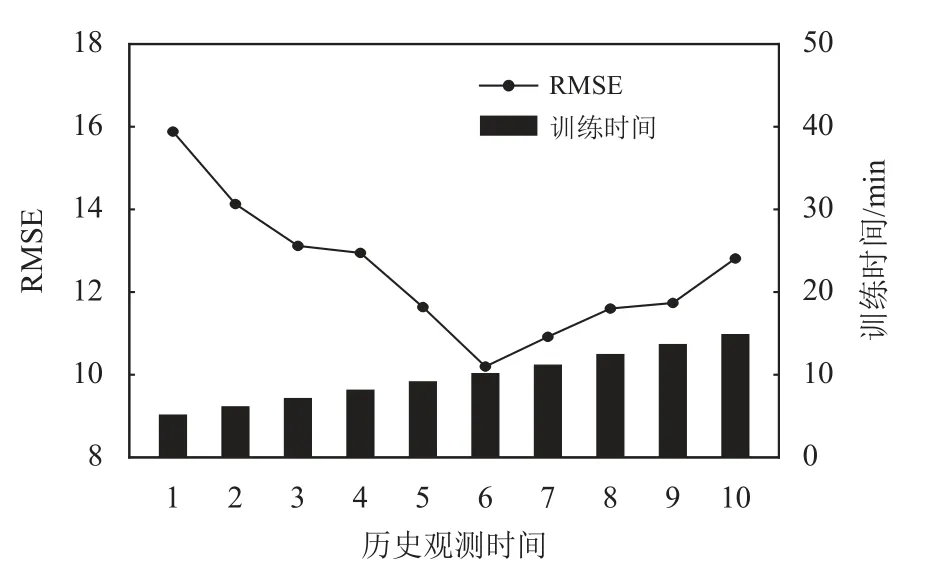
图6 历史观测时间对比Figure 6 Historical observation time comparison

由1.2节可知，DTW算法能够计算目标区域与邻接区域的时间特征相似度，选取图3所示的25个区域为研究对象，区域间的 DTW值如图7所示。颜色从浅到深代表DTW值越来越大。其中，区域自身与自身的颜色最浅，表示自身与自身的DTW最小，最具相关性。为了证明DTW算法对模型预测精度的影响，本节采用消融实验，采用DTW算法的GCNLSTM(DTW)与不采用DTW算法的GCN-LSTM进行多时间步长预测对比。根据所选历史观测时间T=6，设定最大预测时间步长为6，如图8所示。在预测步长1 ～ 6的每一步中，GCN-LSTM(DTW)模型的预测误差RMSE始终低于GCN-LSTM模型，说明DTW算法能够提高模型的预测精度。总体来看，GCN-LSTM(DTW)与GCN-LSTM模型的预测误差RMSE均随着预测步长的增加而增加，这是因为预测误差的累积而导致。

图7 25个区域的DTW值Figure 7 DTW values between 25 zones

图8 多步长预测值Figure 8 Multi-step prediction

4.5 模型泛化能力验证

为了验证GCN-LSTM模型的泛化能力，引入位于纽约市曼哈顿区的乘客出租车打车需求数据集[13]，如图9所示。该区域被划分为63个区，收集的数据范围从2016年1月 ～ 2018年6月。该数据集的处理和时间间隔同4.1节数据集。该地区的乘客需求数据集也被划分为3部分：80%的数据被作为训练数据集；10%作为验证数据集；其余10%为测试数据集。

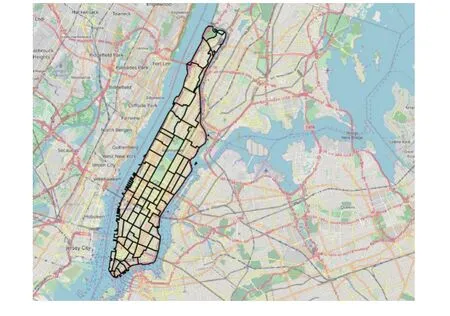
图9 纽约市曼哈顿区的63个研究区域Figure 9 63 zones of study site in Manhattan district, New York City

表2给出7个模型在63个区域中预测的平均RMSE、MAPE、MAE6和预测所用的时间。可以看出，GCN-LSTM模型的误差(RMSE、MAPE和MAE)最小，相较于基于深度学习预测模型(MTL-GRU、GRU、LSTM和TCNN)预测用时最少。这显示了将预测数据转换为图结构数据，模型能够充分发掘区域间的时空特性。由于模型能够同时预测全区域的乘客打车需求，大幅提升了预测效率。传统方法k-NN和SVM因为模型的计算复杂度低，预测63个区域所用时间少于深度学习模型。总之，GCN-LSTM模型在不同规模、不同类型的数据集上表现出良好的预测性能，具有很好的泛化能力。

表2 模型预测效果对比Table 2 Comparison of model prediction results

5 结语

基于图卷积神经网络构建了GCN-LSTM模型，提出一种面向网约车智能调度系统的乘客打车需求预测方法。该方法通过借助DTW算法，将多区域的乘客打车需求构建为乘客需求图，利用GCN提取需求图的空间特征，运用LSTM捕捉区域的时间特征，通过运用基于LSTM的解码器实现同时预测多个区域的乘客需求，并且能够实现多区域的多时间步长预测。通过在城市数据集上开展对比实验，分析GCN-LSTM模型和其他主流模型的预测结果，验证了GCN-LSTM模型的高效性、准确性和较好的泛化能力。