碳限额与碳交易下考虑时间偏好差异的供应链联合减排动态博弈

秦立公，张 勇

(桂林理工大学 商学院，广西 桂林 541004)

碳排放问题是可持续发展中不可避免的问题，引起社会各界的广泛关注。如何进行供应链节能减排、实现可持续发展已成为相关领域学者研究的热点。这些研究切入角度可以概括为供应链结构、供应链渠道、供应链管理方式。在供应链结构方面，程永宏等[1]首次从供应链角度讨论集中与分散决策下单个制造商和单个零售商的最优碳减排和定价策略，以及税率对单位产品碳减排量和销售价格的影响。Bai 等[2]将减排问题引入到按订单生产供应链之中，研究一个供应商供应两种原材料和一个制造商生产两种产品的二级供应链生产运作的利润与碳排放之间的关系，认为在去中心化方案下，供应链整体利润可以得到提升，碳排放量会相应地减少。徐刚等[3]构建一个制造商和两个零售商的二级供应链，通过对不同定价下的供零两主体竞合博弈，分析碳限额对供应链中各成员利润的影响。此外，随着对碳限额与碳交易下的供应链碳减排研究的深入，一些研究将供应链减排问题扩展到由供应商、制造商、零售商组成的三级供应链，但此类研究并未研究在碳限额与碳交易机制影响下的供应链减排问题。在供应链渠道方面，杨磊等[4]将碳排放引入双渠道供应链当中，并建立4种供应链数学模型，讨论双渠道系统中制造商减排率等问题。Ji等[5]、Wang等[6]比较研究不同渠道结构下制造商与零售商联合减排策略。Yang等[7]研究易腐产品的碳排放量对供应链渠道选择的影响，发现设置更大的碳配额并鼓励制造商在没有太多消费者更喜欢在线渠道的情况下开发双渠道模式更为有效。Qi等[8]提出在线渠道价格折扣和离线渠道价格折扣合同，以协调双渠道供应链减排以及利益分配问题。叶欣等[9]考虑双渠道下供应链减排与定价问题。在供应链管理方式方面，Wang等[10]开发了一种博弈模型来分别研究零售商主导和权力平衡情况下的碳减排问题，并指出在零售商占主导地位的情况和权力平衡情况下，成本分摊合同可以实现帕累托最优以改善制造商和零售商的绩效。吴鹏等[11]研究碳配额下企业最优的减排策略，并对比集权和分权供应链的减排效果，发现集权供应链较之分权供应链平均碳排放量低，但总量却较大；分权供应链的中上游企业更倾向于减排。李友东等[12]分别讨论分散决策与集中决策下的制造商主导、零售商主导、垂直纳什3种管理方式下的收益以及减排最优问题。

以上文献中的决策都是假设决策者是理性，不存在任何偏好。但在实际生活当中，决策者们都存在利他偏好、低碳产品偏好、互惠互利、公平关切等各种偏好，而这些偏好对决策者们的决策会产生重大影响。例如，杭州趣链科技有限公司通过对底层交易资产数字化与标准化，并且运用区块链技术达成多方协同合作，完成供应链企业的增信，解决小微企业融资难题等，都属于利他行为。又如，据2020年能源基金会发布的《家庭低碳生活与低碳消费行为研究》报告显示，在购买家电时，低碳环保作为第二大考虑因素占整个样本的54%，这充分说明对低碳产品的偏好会在很大程度上影响人们对产品的选购。因此，很多学者在开展供应链减排问题研究时，会将各种偏好纳入考虑。马秋卓等[13]讨论在碳配额交易体系中，企业面对给定的碳交易价格以及消费者对低碳产品的不同偏好，如何确定目标碳排放量以及最低生产成本，使其获利最高。Xia等[14]将互惠互利的偏好和消费者的低碳意识纳入双向供应链，旨在研究互惠互利和低碳意识如何影响供应链成员的决策和绩效以及系统的效率。Li等[15]分析制造商在可持续能源消耗和低碳生产方面的运营决策将如何随着限额交易政策的变化而发生变化。Jiang等[16]在公平性和总量管制与交易的基础上研究建筑供应链中的碳减排决策和利润分配机制。Kang等[17]指出，企业需要关注消费者的偏好，因为这些偏好的提高将减少长期的运营碳排放。刘云龙等[18]将碳价和消费者低碳意识纳入考虑，发现碳价和消费者低碳意识会直接影响制造商是否会转移减排任务，而减排任务的转移会对制造商和零售商的收益、价格策略等产生一定的影响。Ghosh等[19]考虑碳限额与碳交易政策以及消费者的低碳偏好下对排放敏感的随机需求，来分析两级双渠道供应链模型，并通过考虑产品的兼容性为连锁店供应链运营提供建设性建议。以上文献都是运用静态博弈方法进行研究，但碳排放、低碳认知都是一个动态的过程，且各个决策主体在进行决策时存在一定的偏差。因此，本文在碳限额与碳交易框架下，引入时间偏好差异，对供应链联合减排问题进行相关研究。

本文针对在碳限额与碳交易背景下，少有文献研究三级供应链联动减排，从供应商、制造商、零售商出发，探讨在碳限额与碳交易机制下的联合减排问题，引入时间偏好差异和微分博弈，从动态的视角对供应链联合减排问题进行相关研究，为企业生产发展提供相关建议。

1 问题描述与模型假设

1.1 问题描述与符号说明

本文研究由一个供应商S、一个制造商M以及一个零售商R构成的三级供应链，供应商S负责制造原料并且向制造商M供给原材料；制造商M利用原料生产产品，提供给零售商R。但在整个“原料-产品-商品”过程中都会产生大量碳排放，而在碳交易市场中，国家给定产品的碳排放限额为E，假定国家制定统一的碳交易价格p。若制造商碳排放超出国家配额就需要从其他企业碳排放权购买；若一些企业碳排放剩余，也可以出售碳排放权。面对碳限额与碳交易机制，各级供应链参与者决策时间具有不一致性，即决策时间偏好差异。

同时，供应链中各级参与者为了能够实现低成本绿色生产且满足消费者的低碳偏好进行不同的努力。供应商S 和制造商M提升碳排放率的投入努力分别为kS(t)、kM(t)；零售商的低碳产品的宣传和促销努力为kR(t)。如图1所示。

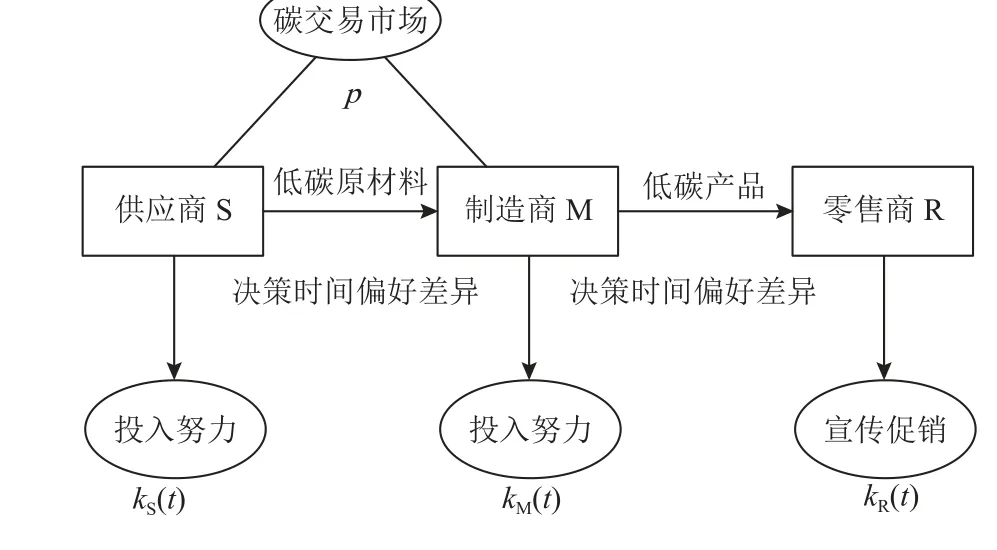
图1 碳限额与碳交易下的供应链减排决策过程Figure 1 Supply chain emission reduction decision process under carbon cap and trade

1.2 模型假设

1) 本文不讨论产品的最优定价问题，因此，假设供应商、制造商、零售商生产和销售商品时的单位利润分别为πS、πM、πR。

2) 在供应链产品生产中，碳排放是一个动态的过程，碳减排量受到供应商减排投入努力与制造商减排投入努力的共同影响，因此本文用微分方程来刻画这一减排过程。

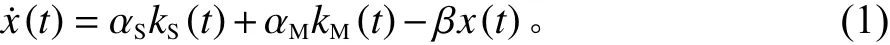
式中，x(t)表 示产品的碳减排量，且x(0)=0；αS与 αM分别表示供应商与制造商减排投入努力对减排量的影响系数；kS(t)和kM则表示供应商与制造商为了减少碳排放量而进行投入的努力水平； β则表示供应链减排自然衰减率。

3) 由于消费者对低碳感知愈发敏感，加之零售商的低碳促销宣传努力，因此消费者对低碳产品越发青睐。本文假设市场是由供应链减排量x(t)、零售商宣传努力kR(t) 组成。

其中，D0为潜在市场； μ1为消费者对低碳产品的偏好系数； μ2为零售商的促销宣传努力对产品需求的影响系数。

4) 假设在碳交易与碳限额背景下，e表示减排后的碳排放量，E为国家分配的碳排放总额度，则减排后总碳排放量为eD，减排后的交易成本为

5) 类似于文献[11-13]的研究，将供应商、制造商的投入努力及零售商的促销宣传努力，与它们的投入成本用凸函数表示。

其中， λS、 λM、 λR分别是供应商投入努力、制造商投入努力、零售商宣传促销努力的成本系数，且都为正数。

6) 供应商、制造商对碳限额与碳交易反映时间存在偏好上的差异，借鉴Harris等[20]的研究，引入时间效用函数Q(T,t)，用以描述决策者的时间偏好差异。

其中，[T,T+τ)是 指现期时间段， [T+τ,∞)指远期时间段； τ服从参数为 ε的泊松分布，且E(τ)=1/η 。当η 趋向于0时，表明现期时间段与远期时间段重合，表明决策者时间偏好相同； φ(0＜φ≤1)表示远期时间段的附加折现影响因子，当 φ越大时，表明对现期偏好越小；当 φ =1时，决策者时间偏好一致。同时假设它们具有相同的贴现率 ρ ＞0。

7) 为了提升供应商投入努力水平和零售商促销宣传努力水平，制造商给予二者一定的补贴nS、nR∈(0,1)。

2 模型建立与求解

2.1 非协同分散决策

在非协同分散决策情境下，供应商提供原材料给制造商，制造商将产品批发给零售商。它们都追求自身利润最大化。制造商作为领导者给予供应商投入补贴，给予零售商宣传促销补贴，以激励生产和销售。三者的决策目标是在无限时间内受益最大化，加之各自不同的决策时间偏好，则三者的目标函数为

利用逆向归纳法，首先求解跟随企业供应商与零售商的决策，之后制造商根据供应商、零售商的最优决策确定投入努力以及给予二者的补贴。则供应商的H JB方程为

零售商通过考虑市场容量、顾客低碳产品偏好、宣传促销低碳产品的成本来确定自身的努力水平，并且满足如下的H JB方程。

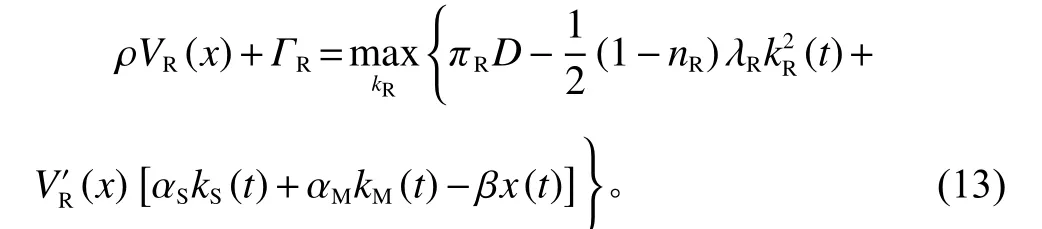
同理，制造商根据供应商及零售商的努力水平进行一定的补贴，以促进低碳产品原料的供应与销售，并藉此确定自身减排投入努力水平，满足如下HJB方程。

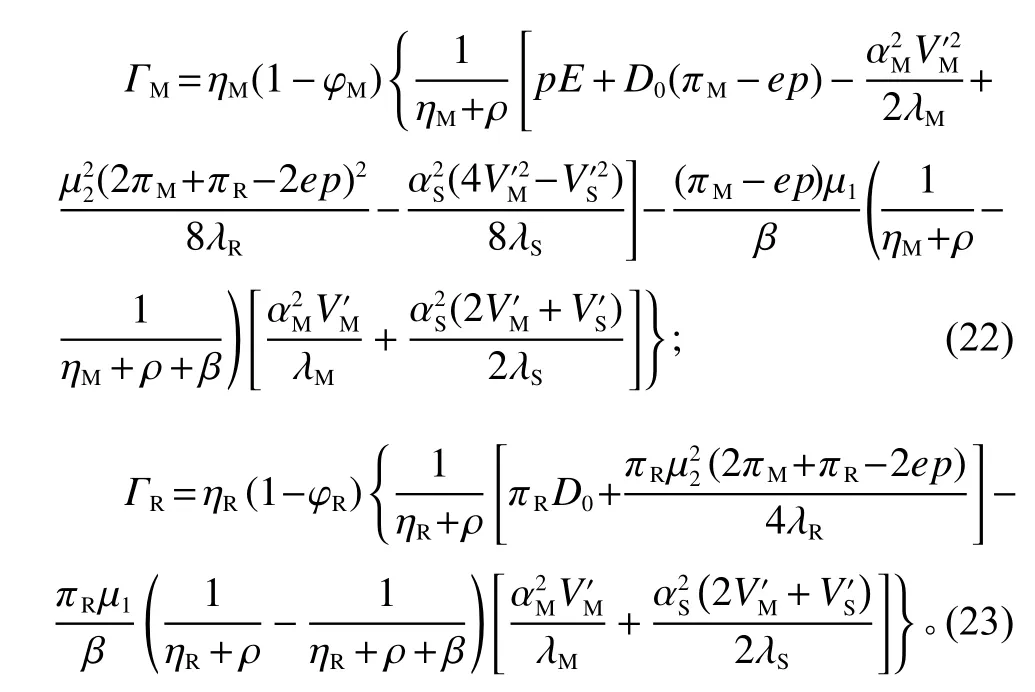
分别假设供应商、制造商、零售商的值函数为一般的一次线性函数：

此时非协同分散决策下的考虑时间偏好差异的供应链联合减排最优策略为

通过以上非协同分散决策的式子，可以发现如下。

1) 制造商对于供应商的减排投入补贴受到制造商自身单位利润πM、 供应商单位利润πS、减排后的排放量e以 及碳价p的 共同影响。当2πM-πS＞2ep时，制造商愿意对零售商促销室外投入进行一定的补贴；而当 2πM-πS＜2ep时，制造商不愿意分担供应商的投入成本。制造商给予零售商宣传促销投入补贴则受到制造商单位利润πM、 零售商单位利润πR、减排后的排放量e以及碳价p的联合影响。当2πM-πR＞2ep时，制造商愿意对零售商促销宣传投入进行一定的补贴；当 2πM-πR＜2ep时，制造商不愿意分担零售商促销宣传的投入成本。

2) 供应商最优减排投入努力k*S与自身投入努力成本系数 λS、 折现率ρ、 供应链减排自然衰减率 β呈现负相关。时间偏好越小，供应商最优减排投入努力水平越高；时间偏好越大，供应商最优减排投入努力水平将会有所减少。同时，消费者对低碳产品的偏好系数 μ1、供应商减排投入努力对减排量的影响系数 αS、 制造商单位利润πM、零售商单位利润πR对供应商减排投入努力具有正向影响。而减排后的排放量e以 及碳价p则表现出负向影响。

3) 制造商最优减排投入努力kM*与消费者对低碳产品的偏好系数 μ1、制造商减排投入努力对减排量的影响系数 αM、 制造商单位利润πM呈正相关；而与自身投入努力成本系数 λM、折现率ρ、供应链减排自然衰减率 β、减排后的排放量e以及碳价p存在负相关关系。

4) 零售商最优宣传促销努力kR*则受到促销宣传努力对产品需求的影响系数 μ2、自身宣传促销成本系数 λR、 制造商单位利润πM、 零售商单位利润πR、减排后的排放量e以 及碳价p联合作用影响。零售商最优宣传促销努力k*R 与促销宣传努力对产品需求的影响系数 μ2、 制造商单位利润πM、零售商单位利润πR存 在正相关关系，与自身宣传促销成本系数 λR、减排后的排放量e以及碳价p呈现负相关关系。这表明零售商在进行低碳产品宣传促销时，应当转变固有的传统宣传思维与方式，创新宣传技术，降低宣传成本，提高宣传效率。

将式 (29) ～ (33)代入式 (20) 中，可得出分散情况下的碳减排量最优轨迹方程为

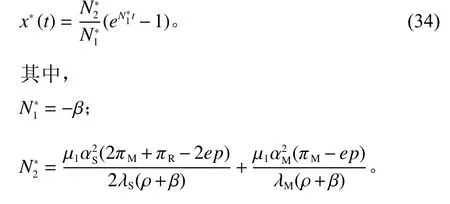
通过以上假设与分析，可得碳限额与碳交易下供应商、制造商及零售商的最优利润函数为

2.2 协同集中决策

在协同集中决策情境下，供应商、制造商、零售商是以整个供应链利益最大化为目标，此时的目标函数为

将式 (39) ～ (41) 代入式 (1) 中，可得协同集中决策下x(t)的轨迹方程为

那么，此时协同集中决策下的考虑时间偏好差异的供应链联合减排最优策略为

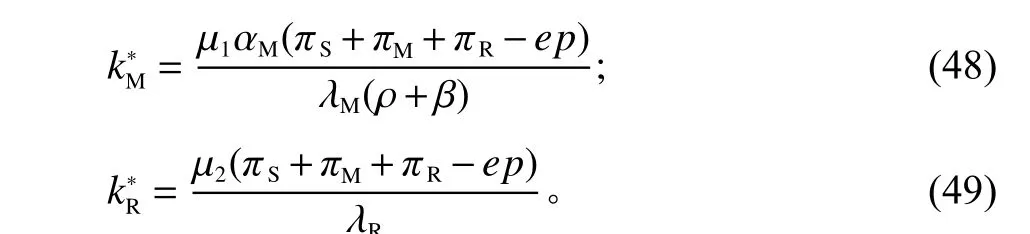
通过以上协同集中决策下的式子，可以发现如下。

1) 供应商最优减排投入努力kS*与消费者对低碳产品的偏好系数 μ1、供应商减排投入努力对减排量的影响系数 αS、 供应商单位利润πS、制造商单位利润πM、 零售商单位利润πR存在正相关关系；而与自身投入努力成本系数 λS、 折现率ρ、供应链减排自然衰减率 β、减排后的排放量e以及碳价p呈现出负相关关系。当πS+πM+πR＞ep时，供应商才会进行减排投入努力提升；当πS+πM+πR＜ep时，供应商不愿进行减排的投入。特别地，当πS+πM+πR=ep时，供应商最优减排投入努力为0。

2) 制造商最优减排投入努力k*M 受到消费者对低碳产品的偏好系数 μ1、制造商减排投入努力对减排量的影响系数 αM、 供应商单位利润πS、制造商单位利润πM、 零售商单位利润πR、自身投入努力成本系数 λM、折现率ρ、 供应链减排自然衰减率β、减排后的排放量e以及碳价p等 诸多因素供应影响。当 λM、ρ、 β、e、p越大时，最优减排努力水平越低；反之，则越高。

3) 零售商最优宣传促销努力kR*则与促销宣传努力对产品需求的影响系数 μ2、 供应商单位利润πS、制造商单位利润πM、 零售商单位利润πR呈正相关；与自身宣传促销成本系数 λR呈负相关。

将式 (29) ～ (33) 代入式 (20) 中，可得出分散情况下的碳减排量最优轨迹方程为

3 数值仿真

为了更为直观地比较不同决策下碳减排、供应链各方价值等相关情况，本文利用数值分析方法进行分析。根据前文中假设，对相关参数进行取值：p=0.3， μ1=5， μ2=6， αS=2， αM=3，πS=4 ，πM=5，πR=6， λS=10 ， λM=12 ，λR=13，e=1，E=20 ，ρ=0.2 ， β=1。将这些参数的取值代入式(34)、(50)之中，可得非协同分散决策与协同集中决策下的碳减排轨迹图，如图2所示。

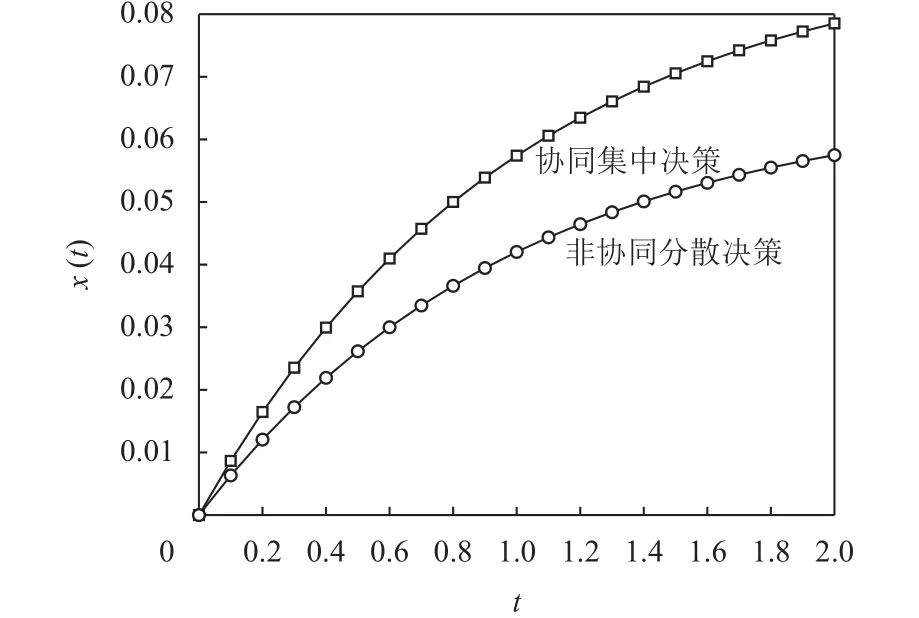
图2 碳减排轨迹曲线Figure 2 Carbon emission reduction trajectory curve

两种决策情形下，碳减排随着时间推移会不断增多，但后期增速变缓，最后保持在一个稳定的状态。这表明当供应链各方开始减排初期，碳减排量较大，但随着减排难度不断增大，碳减排量也会相应地减少。协同集中决策下碳减排量始终大于非协同决策下的碳减排量，说明协同决策较之非协同决策更有利与增加碳减排，减少能耗，开展绿色生产。

根据图3 ～ 5，可以发现，供应商、制造商、零售商的时间偏好一致时的价值始终位于时间偏好不一致时价值的上方，表明对于三方来说时间偏好一致的价值始终大于时间偏好不一致时的价值。而根据图6和图7，可以发现，无论是在非协同分散决策还是协同集中决策，对于一个三级供应链，时间偏好一致时的价值大于时间偏好不一致时的价值。

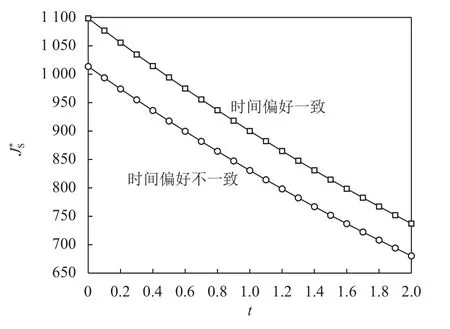
图3 供应商最优价值Figure 3 Supplier's optimal value

图4 制造商最优价值Figure 4 Manufacturer's optimal value

图5 零售商最优价值Figure 5 Retailer's optimal value

图6 非协同分散决策下供应链整体价值Figure 6 Supply chain value under non collaborative decentralized decision making

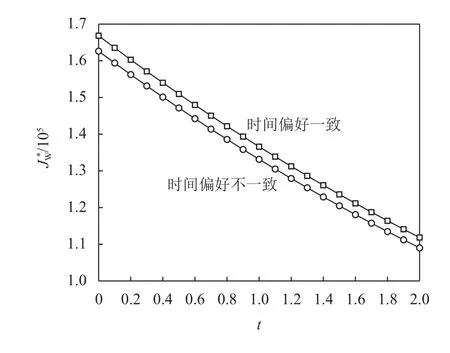
图7 协同集中决策下供应链整体价值Figure 7 Supply chain value under collaborative centralized decision making

同时，本文对供应链减排自然衰减率 β与碳减排，减排后的碳排放量e与供应链价值之间的关系进行数值仿真，如图8 ～ 11。

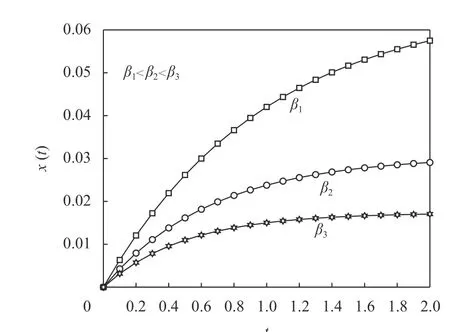
图8 非协同分散决策下 β对碳减排的影响Figure 8 Impact of β on carbon emission reduction under non collaborative decentralized decision making

根据图8与图9可以发现，随着供应链减排自然衰减率 β逐渐增大，无论是在非协同分散决策还是协同集中决策下，供应链整体碳减排量不断减少。这说明供应链自然衰减率越高，企业进行碳减排技术投入将会不断增加，进而导致成本不断增加，但减排难度不断增加，所以碳减排量会相应减少。图10与图11则表明在非协同分散决策与协同集中决策下，e越大对供应链整体价值的影响越大。相较于非协同分散决策，e对协同集中决策下的供应链整体价值影响更大。

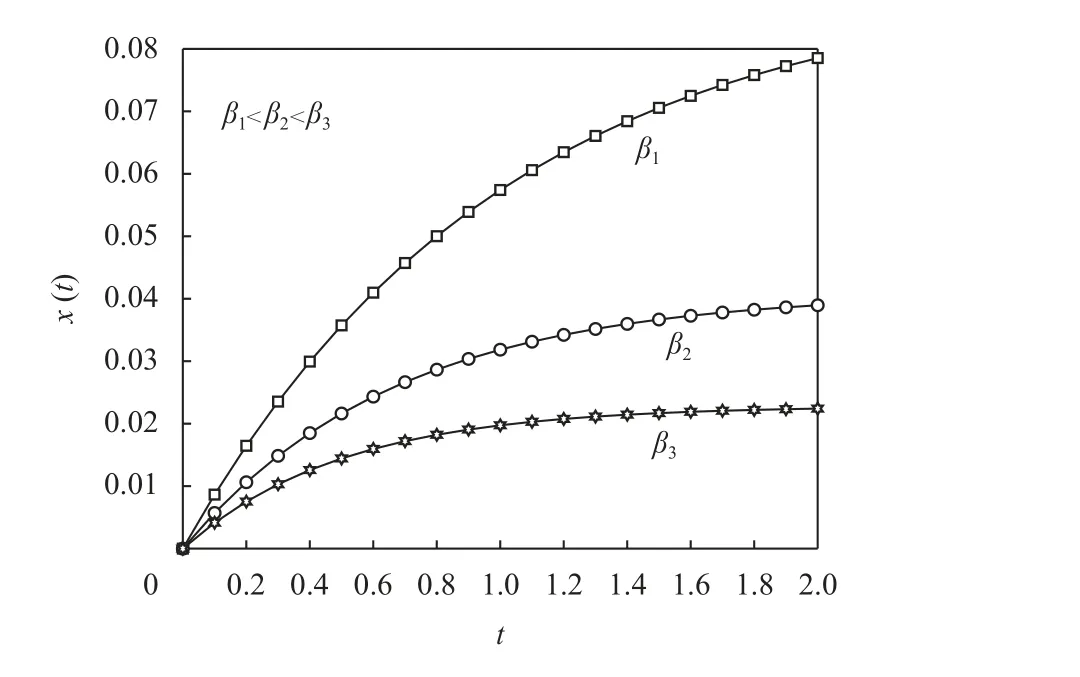
图9 协同集中决策下 β对碳减排的影响Figure 9 Impact of β on carbon emission reduction under collaborative centralized decision making

图10 非协同分散决策下e 对供应链价值影响Figure 10 Impact of e on supply chain value under non-collaborative decentralized decision making

图11 协同集中决策下e 对供应链价值影响Figure 11 Impact of e on supply chain value under collaborative centralized decision making

4 结语

本文在碳限额与碳交易的框架下，建立起由供应商、制造商、零售商构成的三级供应链，并引入时间偏好差异、微分博弈论从动态的角度研究供应链减排问题，得出如下结论。

1) 协同集中决策下的碳减排量以及供应链整体价值均高于非协同分散决策下的碳减排量以及供应链整体价值。这表明在协同集中决策下供应链各方价值等更容易达到帕累托最优。

2) 时间偏好一致的供应链决策者所获取的价值始终高于时间偏好不一致的供应链决策者所获取的价值，并且时间偏好不一致程度加剧了决策者所获取的价值变化幅度。这表明供应链的参与主体供应商、制造商、零售商在决策过程中，如果对远期效益存在偏好，在减排过程中往往能获得较高的收益。

3) 供应链减排自然衰减率对供应链整体价值影响大，供应链减排自然衰减率越大，会导致供应链整体价值大幅减少。所以，在碳限额与碳交易机制下，供应链各方决策者应当充分考虑整个供应链的长远减排能力，相 应 地提升 μ2、 αS、 αM等相关 系数，降低供应链减排自然衰减率，提升供应链减排能力，为构建绿色循环经济提供充分保障。

本文着重研究考虑时间偏好的供应链减排问题，因而没有考虑原材料、产品、商品的折现因子差异；同时未对碳限额与碳交易下不确定市场情形进行研究。这些都是后续值得研究的。