锥台嵌挤预应力约束混凝土的抗侵彻性能*

王子国，王松涛，孔祥振，孙宇雁

（1. 青岛理工大学土木工程学院，山东 青岛 266520；2. 陆军工程大学爆炸冲击防灾减灾国家重点实验室，江苏 南京 210007）

混凝土广泛应用于军民用防护工程，是遮弹层、核电站防护墙[1-2]等防护结构的主要材料。弹体侵彻作用下，混凝土防护结构（如遮弹层）易发生开坑和震塌等脆性破坏，严重影响其抗侵彻性能。通过钢管、纤维增强树脂等韧性材料约束混凝土，不但可提高混凝土材料的韧性、限制径向裂缝的产生和发展，而且约束效应使得混凝土处于三向围压状态，可显著提高其抗侵彻性能[3-5]。

在钢管约束混凝土抗侵彻性能的研究中，石少卿等[6-8]提出了约束混凝土遮弹层结构，该结构以正方形和正六边形的约束混凝土为基础单元，通过紧密铺设形成遮弹层，研究发现弹体侵彻时的破坏区域限制在单个基础单元内，破坏面积明显减小。王起帆等[9]对钢蜂窝约束混凝土遮弹层和普通钢筋混凝土遮弹层分别进行了侵彻实验，发现蜂窝约束混凝土遮弹层结构的抗弹性能明显优于普通钢筋混凝土遮弹层。甄明等[4]和万帆[5]开展了一系列小直径钢管约束混凝土的抗侵彻实验，探讨了钢管约束混凝土的抗单次侵彻性能和抗多次侵彻性能，发现钢管约束混凝土直径越小，其抗侵彻性能越好。蒋志刚等[10]对圆形钢管约束混凝土的抗侵彻性能进行了数值模拟，发现钢管约束混凝土的抗侵彻性能优于无钢管约束的混凝土，性能提高约15%。考虑到靶体在侵彻过程中受到外围钢管的约束作用，混凝土近似处于三轴应力状态，徐松林等[11]、陈丽娜等[12]和单俊芳[13]基于混凝土三轴应力实验装置，进行了不同侧限应力水平下立方体混凝土靶抗弹体低速侵彻实验，发现在侧限状态下，弹体侵彻阻力随着靶体侧限应力的增加而逐渐增加。

陶瓷作为一种脆性材料，采用类似的约束方式同样可以提高其抗侵彻性能。Sherman 等[14]对无侧向约束和有侧向约束的Al2O3陶瓷板抗弹体侵彻性能进行了实验研究，发现无侧向约束的陶瓷板破坏严重，而有侧向约束的陶瓷板保持完整，且具有更好的抗侵彻性能。Orphal 等[15-17]对受三向约束（预应力）的B4C、SiC、Al2O3等陶瓷材料抗钨合金杆弹的侵彻性能进行了实验研究，发现陶瓷靶的抗侵彻性能随着侧向施加预应力的增大而增加。Hu 等[18]对AlN 陶瓷进行了单轴静动态压缩和受限动态压缩实验，发现当围压增加至2 GPa 以上时，AlN 陶瓷不再发生脆性破坏而发生延塑性破坏。Zhang 等[19]通过实验和数值模拟研究了预应力对陶瓷-金属复合装甲的抗侵彻性能的影响，发现预应力陶瓷迫使弹体产生塑性变形和磨蚀，且弹道极限提高了25%以上。

可以看出，目前预应力约束陶瓷抗侵彻性能的研究成果比较丰富，但是对于预应力约束混凝土材料的抗侵彻性能的研究相对较少。现有对陶瓷施加预应力的方法中主要有机械挤压法[14-18,20-21]和热装法[19]，机械挤压法通过螺栓等机械装置移动侧板直接挤压陶瓷板的侧壁施加预应力，该方法较复杂、不便于在实际工程中应用；而热装法是将陶瓷装入高温下的金属套箍内，然后整体降温，热膨胀系数较大、收缩更快的金属套箍压缩陶瓷从而施加预应力，但由于混凝土不能承受高温，该方法不适用于混凝土材料。

本文中提出一种通过锥台嵌挤方式对混凝土施加预应力的方法，即通过锥台体的下压深度或推入荷载大小控制预应力的大小，并通过数值模拟验证该方法的可行性。在此基础上，系统地分析预应力大小、钢约束环强度、混凝土强度、含钢率和弹体速度等参数对预应力约束混凝土靶体抗侵彻性能的影响。

1 预应力方案设计

1.1 施加方法

如图1 所示，采用楔形块楔紧的原理，将圆锥台或者正六棱锥台等锥台形混凝土靶体强行挤入对应形状的约束环内，通过锥面配合契紧的方式对靶体施加预应力，在推力作用下锥台形靶体的围压（预应力）随挤入深度的增加而增大。预应力约束靶体的中心轴线剖面及预应力施加方法如图2 所示，设锥台体和约束环内壁具有相同的锥面倾角α 和相同的高度h1，将锥台放入支撑平台上的约束环内，此时锥台直径与约束环内径的盈差为δ，如图2(a)所示；进而沿高度方向将锥台强行挤入约束环内产生预压应力σ（图2(b)）；达到预定位置后的预应力约束靶体如图2(c)所示。当锥面倾角α 一定时，若满足锥台靶小端直径d2小于约束环大端口内径d1，且预应力施加过程中锥台靶体和约束环均未破坏，则盈差δ 和对应的下压深度h越大，预压应力 σ 也越大。

1.2 工况设计

以圆形靶体为研究对象，靶体由圆锥台形混凝土靶和与之契合的变壁厚钢约束环构成，几何尺寸如图3 所示，两组件的高度h1均为50 mm，钢环上端口内径d1=100 mm。在设计锥面倾角α 时，过大的倾角会引起过大下推阻力和锥面损伤，也会导致锥台反向滑动或者滑出，因此经大量试算，试件的锥面倾角α 取为3°。

通过设计下压深度h及与其对应的盈差δ，可得到不同的预应力。表1 中给出了本文中设计的8 种工况，下压深度每增加2 mm 为1 个等级，共8 级，靶体的径向预应力随下压深度的增加而增大，最大下压深度14 mm。

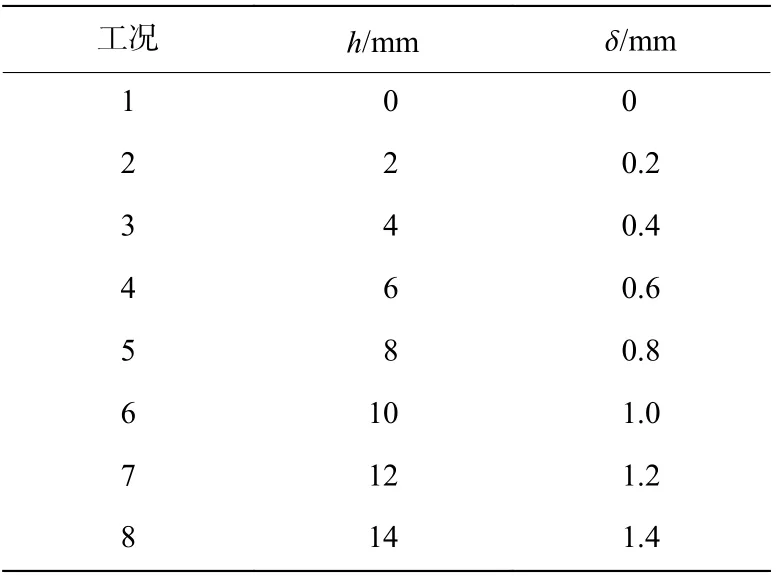
表1 预应力工况设计Table 1 Designed pre-stress conditions

2 预应力施加和弹体侵彻数值模型

通过数值模拟验证锥台嵌挤方法对圆锥台混凝土施加预应力的可行性，并进一步研究预应力约束混凝土圆锥台的抗侵彻性能。采用显式有限元程序LS-DYNA 进行模拟，为提高计算效率，有限元模型均采用1/4 模型，靶体材料、弹体、钢约束环及垫板均采用三维实体单元进行模拟。

2.1 有限元模型

采用7.62 mm 口径弹体，几何模型和有限元模型如图4(a)所示，网格尺寸为1 mm。图4(b)中给出了钢环靶体的有限元模型，由约束环、圆锥台、弹体、垫板和推力块组成，为兼顾效率和精度，以圆锥台为中心、半径15 mm 范围内为加密网格，其余部分网格向四周放射加粗。

2.2 材料模型

混凝土材料强度设为120 MPa，采用Holmquist-Johnson-Cook（HJC）材料模型[22]描述，该模型形式简单，广泛应用于爆炸或者冲击作用下混凝土类材料的动态力学响应分析[23]。该模型参数主要包括基本力学参数、强度和率效应、状态方程和损伤等19 个参数，准确确定上述参数需要一系列实验数据。本文中参考Holmquist 等[22]给出的HJC 本构模型参数和Ren 等[24]修正后的高强混凝土HJC 本构模型参数。

约束用钢环材料采用LS-DYNA[25]中的随动硬化模型，屈服强度取为1 200 MPa、弹性模量210 GPa、泊松比0.3，并通过Cowper 和Symonds 模型[26]考虑其应变率效应，主要参数取值参见文献[27]。

Johnson-Cook 模型能够模拟子弹在侵彻过程中的大应变、高应变率、高温环境下的失效过程。因此，本模拟采用Johnson-Cook 材料模型模拟30CrMnSiNi2A 超高强度钢（锰铬钢）子弹，弹体材料参数参见文献[28]。此外，由于垫板与推力块不是主要研究对象，故推力块采用与钢环相同的材料模型，垫板则采用刚体描述。

2.3 加载流程

数值模拟中，混凝土圆锥台的加载流程包括第1 阶段准静态预应力加载和第2 阶段的瞬态弹体侵彻，如图5 所示。

在第1 阶段的预应力加载中，加载结束后施加全局阻尼使得应力快速平衡。注意到锥台下推速率可能会影响到最终稳定的预应力大小，本文中以下推深度h为10 mm 为例，选取0.1、0.5、1、5、10 m/s 等5 种下推速率分析加载速率对稳定预应力的影响，如图6 所示。可以看出，当下推速率小于1 m/s 时，对最终形成的稳定预应力影响较小，因此综合考虑计算精度与效率，以下数值模拟中下推速率取为1 m/s。

第1 阶段结束后采用重启动策略，即第1 阶段计算结束后终止计算，但保留应力状态及损伤信息，进而增加弹体进行侵彻的第2 阶段计算，可大幅提高计算效率。已有研究[29]表明靶体网格大小对数值模拟的准确性影响较大，同样以圆锥台下推深度h为10 mm 为例，选取加密区网格尺寸为0.25、0.5、1、2 mm 进行网格敏感性分析（弹体速度取为600 m/s）。图7 中给出了网格尺寸对侵彻深度的影响。可以看出，网格尺寸小于1 mm 时对侵彻深度的影响较小，综合考虑计算效率和精度，以下网格尺寸取为0.5 mm。

3 数值模拟结果的分析与讨论

基于表1 中给出的8 种预应力施加工况，首先分析预应力分布规律及其与下压深度的关系，再进一步根据各预应力工况侵彻下的靶体损伤云图和侵彻深度分析预应力对靶体抗侵彻性能的影响。

3.1 预应力加载

根据表1 中的8 种工况将锥台推入后，形成稳定的von Mises 应力云图，如图8 所示。可以看出，混凝土圆锥台和钢环的预应力随下压深度h的增大而增大，下推14 mm 工况的圆锥台内部应力分布出现了明显的突变，这是预应力过大导致出现了局部损伤（后续会进一步分析），其他各工况的圆锥台均未见损伤。

为了进一步观察圆锥台和钢环的预应力分布规律，以下推深度12 mm 为例，在靶体中心和钢环中心轴线上等间距分别取6 个单元（见图9），用以观测各单元径向应力的分布规律。

靶体中心各单元（单元1～6）的径向应力（压应力为正）分布时程曲线如图10 所示。可以看出，各单元径向应力为压应力且很快趋于稳定，由于钢环的壁厚从上至下呈线性增厚，靶体内部径向压应力从上至下随着钢环的壁厚增加呈近似线性增大。鉴于混凝土靶体的应力分布不均，本文中采用上述6 个单元的径向应力平均值代表靶体的整体预应力水平。预应力水平与下压深度h和盈差δ 的关系曲线如图11 所示，可以看出，靶体预应力随着下压深度和盈差的增大而近似线性增大。当下压深度为12 mm 时，靶体中心单元的径向压应力达到256 MPa，约为混凝土单轴压缩强度的2 倍，使得混凝土处于强围压状态，可提高其抗侵彻性能。上述讨论验证了通过推压方式实现预应力加载的可行性。

钢环截面中心单元的环向应力和等效塑性应变时程曲线如图12 所示，可以看出，钢环内部环向应力由上至下逐渐减小，其环向应力最大可达到1 900 MPa，超过了钢材的屈服强度（1 200 MPa）。考虑到实际工程中这种高强度钢材比较难获取，将在后续参数敏感性分析中详细讨论钢环强度对预应力的影响。

3.2 弹体侵彻

为表征预应力对抗侵彻性能的影响，定义侵彻深度下降率为：

式中：hp为有约束有预应力条件下的侵彻深度，h0为有钢环约束但无预应力条件下的侵彻深度。

以弹体初速度600 m/s 为例，8 种工况下靶体在侵彻前（0.015 ms）和侵彻后（0.2 ms）的损伤云图如图13所示，结合图14 所示的侵深下降率（R）与预应力的关系曲线、以及图15 所示的弹体加速度时程曲线可以看出：随着预应力的增加，靶体损伤破坏区域变小、侵彻阻力逐渐增大、侵彻深度逐渐减小；当下压深度为12 mm，即施加在圆锥台的中心预应力为256 MPa 时，其侵彻深度比有钢环约束而无预应力的混凝土圆锥台下降了21%，抗侵彻性能达到最佳。但当预应力超过一定限度（比如下压深度为14 mm）时，在预应力施加结束后（弹体侵彻前）混凝土内部就已经出现了裂纹（见图13），导致靶体对弹体阻力减小（见图15），进而使得其抗侵彻性能大幅下降（见图14）。需要指出的是，为便于分析，混凝土材料采用了HJC 模型描述，其主要适用于侵彻等以压缩应力状态主导的情况，而未考虑拉伸损伤，可能会导致对预应力施加（侵彻前）损伤状态的预测不准确，但不影响本文结论的一般性。为解决该问题，后续研究将采用修正的HJC 模型[30]、邓国强等提出的JHR-TCK 模型[31-32]或Kong-Fang 模型等[23]。

4 参数敏感性分析

基于上述预应力工况（基准工况），采用相同的数值模型和计算方法进行参数分析，在其他参数不变的条件下，仅改变钢环强度、混凝土强度、含钢率或者弹体速度等参数中的一种参数，研究其对靶体的预应力及抗侵彻性能的影响规律。

4.1 钢环强度的影响

选取300、600、900 MPa 等3 种不同强度等级的钢环进行参数分析。如图16 所示，从靶体下压深度h与预应力和侵深下降率R的关系曲线可以看出，混凝土靶体压入钢环内初期，预应力和侵深下降率R随着下压深度的增大呈近似线性增大。对于屈服强度较低的钢环，较小的下压深度就能使其进入塑性阶段，随后预应力逐渐进入平衡阶段，几乎不再增加，对应的混凝土靶体侵深下降率R也几乎不再增加，因此钢环强度越低，能提供的预应力越小，靶体抗侵彻性能提高幅度也越小。但如果钢环屈服强度过高，如屈服强度为1 200 MPa 时，其虽然具备提供足够大预应力的潜力，但若预应力超过一定程度，靶体内便会产生损伤（见图13），进而导致预应力和侵深下降率R骤降，使得钢材强度不能充分发挥。因此合理匹配钢环强度和混凝土强度，能够同时提高材料强度利用率和抗侵彻性能。

4.2 混凝土强度的影响

选取强度为70、90 和150 MPa 的混凝土靶，分析混凝土强度对预应力大小和抗侵彻性能的影响，计算结果如图17 所示。可以看出，各强度混凝土靶体的预应力均随下压深度h线性增加，相应的侵深下降率R均随预应力的增大而增大，但增幅逐渐变小并趋于稳定。值得注意的是，对于强度相对较低的混凝土靶，当预应力过大时将发生如图13 所示的破坏形式，导致靶体的抗侵彻性能大幅降低。

4.3 含钢率的影响

钢环约束混凝土靶体的含钢率可以通过改变钢环壁厚或者改变混凝土靶体直径的方式进行调控。前一种方式是在锥面倾角不变的情况下，设混凝土直径不变，通过改变钢环外径调节壁厚的方法调整靶体含钢率；后一种方式是设钢环壁厚不变，通过改变混凝土直径调整靶体含钢率。选取上端口壁厚为2、10、15 mm 等3 种规格的钢环，对应的含钢率分别为15%、53%、80%；选取大端直径为200 和400 mm 等2 种直径的混凝土靶，对应的含钢率分别为7%和2%。结合基准工况试件（含钢率为29%，上端口壁厚为5 mm，混凝土靶大端直径为100 mm）分析讨论含钢率对靶体抗侵彻性能的影响。

考虑到含钢率对没有施加预应力条件下的混凝土靶抗侵彻性能有影响，在分析中增加了含钢率为0 的情况。图18 为在无预应力条件下，含钢率为0（素混凝土）、2%、7%、15%、29%、53%、80%时靶体的侵彻深度变化规律。由图可知，当靶体含钢率从0 增加至2%时，靶体侵彻深度快速下降，但进一步增加含钢率时，靶体侵深几乎不变，说明单纯增加靶体含钢率来提高抗侵彻性能效果有限且不经济。

利用上述钢环对混凝土靶施加预应力，如图19（a）所示，可以看出预应力同样随下压深度h的增大呈线性增大，而且含钢率越大，预应力增速越快，但当预应力过大时，同样会出现图13 所示的损伤破坏，导致靶体预应力和抗侵彻性能大幅降低。图19（b）中给出了靶体侵深下降率R随下压深度的变化曲线，可以看出R随下压深度的增大而增大，但增幅逐渐变小并趋于平缓；当含钢率为15%时，靶体预应力可达113 MPa，其侵深下降率R达到19%（相对于有约束无预应力靶），非常接近基准工况（含钢率为29%，侵深下降率为21%），且该预应力已经非常接近其自身能够提供的极限预应力；因此，当含钢率为15%时，靶体受预应力约束后的抗侵彻效果和钢环利用率都能达到较高的水平。但是含钢率过低时给靶体提供的预应力很小，如靶体含钢率为2%时，预应力最大仅为4 MPa，对提高其抗侵彻性能的作用非常有限。

综上所述，在混凝土可承受的预应力范围内，靶体含钢率越高，钢环能够提供的预应力潜力越大，对提高靶体抗侵彻性能的作用越明显。这是由于当靶体含钢率越高，钢环可提供的预应力潜力就越大，侧向约束效果越好，混凝土强度也越高，相应的弹体侵彻阻力随着靶体侧限应力的增加而提高，因此靶体的抗侵彻性能的提高最终是依靠侧向预应力的增加而提高。但靶体含钢率过小时，给混凝土靶体提供的预应力潜力过低，对靶体抗侵彻性能的提高有限。考虑到靶体抗侵彻性能并非随含钢率及预应力的增加而无限制提高，因此需要平衡材料利用率和靶体的抗侵彻性能的关系，选择适当的靶体含钢率，提供足够大的预应力，才能更有效地提高靶体的抗侵彻性能和材料利用率。

4.4 弹体初速度的影响

分别取100～800 m/s 等8 种弹体初速度侵彻靶体，探讨弹体速度对预应力约束混凝土抗侵彻性能的影响，结果如图20 所示。可以看出，弹体速度越高，预应力对提高抗侵彻性能的作用越明显，当弹体初速度为800 m/s、预应力为256 MPa 时，侵深下降率可达27%。

5 结 论

提出了一种锥台嵌挤预应力约束混凝土提高其抗侵彻性能的方法，采用数值模拟验证了该方法施加预应力及提高抗侵彻性能的可行性，并进一步探讨了预应力大小、钢材强度、混凝土强度、含钢率和弹体初速度等参数对抗侵彻性能的影响，得到以下结论。

(1)锥台嵌挤的方式能够较为简便地对混凝土靶施加预应力，可以通过锥台靶体的下压深度、盈差以及压入力的大小等指标控制预应力大小，且靶体预应力随着其下压深度和盈差的增大而近似线性增加，为实际工程应用提供较为可行的方法。

(2)预应力对混凝土靶的抗侵彻性能影响显著，在一定范围内预应力越大，钢环约束混凝土靶的抗侵彻性能越好，但预应力过高时，由于靶体内部发生损伤导致其抗侵彻性能反而快速下降。

(3)高强度钢环能够提供的预应力潜力大，对提高抗侵彻性能效果明显；合理匹配钢环强度和混凝土强度，能够同时提高材料利用率和抗侵彻性能；预应力对抗侵彻性能的影响随弹体初速度的增加而增大。

(4)选择适当的含钢率，可有效提高靶体抗侵彻性能和钢材利用率，如靶体含钢率为15%时，靶体的抗侵彻性能可提高19%，最优含钢率有待进一步研究。

(5)本文方法虽针对混凝土遮弹层提出，但基本方法和原理可应用于抵御弹体侵彻和破片冲击的结构，如防护门面层、导弹井盖以及预应力约束陶瓷复合装甲等。