水声通信中极化码的应用研究
邢莉娟,李 卓,张泽栋
(西安电子科技大学综合业务网国家重点实验室,陕西西安 710071)
1 引言
由于电磁波和光波在水下衰减严重且传播距离短,声波是水下无线通信首选的信息载体.然而水声信道因其具有时-频-空变特性,被认为是迄今为止难度最大的无线通信信道之一,其具体表现为强多途、大起伏、窄带宽及高噪声干扰,因此在水声信道实现稳健通信是一个严峻的挑战.其中高传输速率、低误码率是目前水声通信(Underwater Acoustic Communication,UWA)重点研究的技术目标[1].
近二十年来,研究人员在认知水声传播规律和信道特性、提高水声通信速率和距离、对抗信道衰落和起伏等方面进行了大量的研究探索;同时,得益于信号处理理论技术的突破和计算机性能的跃升,联合均衡译码[2,3],近香农限信道编译码、多载波调制[4]、多输入多输出[5]等一系列先进的通信信号处理技术先后涌现并得以引入到水声通信领域[6],取得了许多性能优异的实验结果,部分技术已经开始转入工程化应用.
其中,信道编码技术被认为是必不可少的关键环节之一.为克服浅海水下数据传输的强干扰性与强衰落性,强有力的信道纠错码技术被引入水声通信中[7,8],以保证在较低信噪比下水声数据传输的可靠性.目前水声通信中已引入了如Turbo码、RA(Repeat Accumulate)码、LDPC码及喷泉码等高效信道编码技术[9],其中LDPC码在水声通信中的应用较为成熟.信道编码界刚刚兴起的极化码性能表现优异,在2016年的3GPP RAN1 #87会议中,在与美国经典的LDPC码和法国提出的Turbo 2.0码竞争下,最终中国主推的Polar Code方案力排众议,成为了5G系统增强型移动带宽(enhanced Mobile Broadband,eMBB)中控制信道的编码方案,新兴的极化码在信道编码领域证明了其未来可期,但在水声通信中还没有深入的研究.
本文针对三种典型的水声信道模型,分析了这些信道模型下的极化现象,提出了一种采用蒙特卡洛构造方法的极化码构造方案.在不同的水声信道模型下的仿真结果表明,相比于码长相近的LDPC码,文中构造的极化码的纠错性能整体而言要优于LDPC码,同等误码率要求的情况下,可以有效的节省功率开销,提高编码增益,证明了极化码这个新兴的纠错编码方案在水声通信系统中具有很强的竞争力.
2 极化码的基本原理
极化码作为近年来信息编码领域一项新的重大进展,是现今唯一一类数学可证明能够达到香农容量限的纠错码.2009年Arikan提出二进制输入离散无记忆对称信道(Binary-input Discrete Memoryless Channel,B-DMC)下的极化码理论,给出二元删除信道(Binary Erasure Channel,BEC)下的递归构造方法和具有线性译码复杂度的串行抵消(Successive Cancellation,SC)译码算法[10].随后Vardy提出了保留多条候选路径的串行抵消列表(Successive Cancellation List,SCL)译码算法,大大提高了极化码的译码性能,并在此基础上引入循环冗余校验(Cyclic Redundancy Check,CRC)对候选路径进行筛选,由于CRC的漏检概率非常低,循环冗余校验辅助的串行抵消列表(CRC-aided SCL,CA-SCL)译码算法下极化码的性能甚至可以趋近最大似然(Maximum Likelihood,ML)译码的性能[11].
极化码的基本思想,是通过N次独立使用物理信道W进行信道合并和拆分的操作,实现合成子信道对称容量两级分化的过程(当码长为N时).首先通过信道合并将N个B-DMC信道W通过线性变换操作合并成一个合成信道WN,再通过信道拆分操作将WN拆分成N个子信道.当N趋于无穷大时,最终合成的信道中一部分子信道是信道容量为1的无噪声信道,用于传输信息比特,另一部分是信道容量为0的纯噪声信道,用于设置收发端都已知的冻结比特.
如图1所示,极化码的信道合并和拆分的过程可以用一个线性变换矩阵GN来等效描述,使用aji=(ai,ai+1,…,aj)表示向量,其中uN1表示输入序列,xN1表示经过线性变换矩阵后的码字序列,yN1表示x1N经过信道W传输后的输出序列.极化码的等效生成矩阵可以表示为GN=BNF⊗n,其中表示Kronecker 积,矩阵BN为位反转操作矩阵.基于密度进化、高斯近似、蒙特卡洛统计等方法,可以计算跟踪极化子信道的可靠度.针对码率为R=K/N的极化码,最终选出可靠度最高的K个子信道,其信道索引集合记为A.对于码长N=2n,n≥0的极化码,其中n表示极化层数,其编码输出序列为,可以分解表示为:

图1 极化码的编码过程
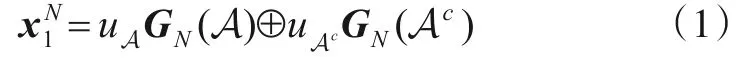
其中GN(A)表示信息位集合A对应行构成的GN子矩阵,Ac表示集合A在{1,…,N}中的补集,uA代表信息比特,uAc代表冻结比特,⊕表示模2加法运算[10].极化码的构造主要是通过计算极化操作后各个子信道的可靠度,挑选出K位信息位索引的工作.
3 系统仿真模型
为了研究极化码在水声通信中的性能表现,设计了系统框图如图2所示.首先发送初始比特流,完成编码后,进行二进制相移键控调制(Binary Phase Shift Keying,BPSK)调制,随后信息经过三种典型的水声信道,并加入加性高斯白噪声(Additive White Gaussian Noise,AWGN).接收端完成进行自适应判决反馈均衡[12,13](Decision Feedback Equalizer,DFE)后,进 行BPSK解调,然后进行CA-SCL译码,并最终根据译出的数据比特与发送端的初始比特进行对比以统计错误比特数量并计算极化码在各个信道下的误码率,为了与LDPC码作横向比较,衡量其性能的指标选取为误比特率(Bit Error Rate,BER).
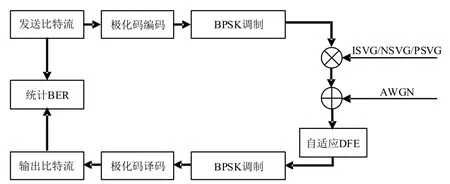
图2 水声通信系统仿真框图
极化码在水声通信系统中的仿真实验的重点主要为两个部分,第一部分为极化码的构造部分,由于水声信道为典型的非对称信道,所以极化码的构造方法选取蒙特卡洛构造方法.第二部分为极化码的译码部分,综合译码算法的性能与算法实现的复杂度,最终选取CA-SCL译码算法作为译码方案.
4 水声信道模型
实际水声信道的传输函数是时-频-空变的,不同海域的信道状况会有很大不同.但在相干时间范围内,可认为其转移函数不随时间变化.本文将针对声速为常数的等温层模型、负声速梯度信道模型和正声速梯度信道模型进行极化码的性能仿真研究.
为设计特定的水声通信系统通常是先在特定海域进行实验测量,获取的数据对该海域水声信道的统计特征进行评估,并以此为设计参考.目前,在水声信道建模方面广泛使用的是多途传播模型,它是基于射线声学原理建立的.通常情况下,水声通信系统可以被描述为:
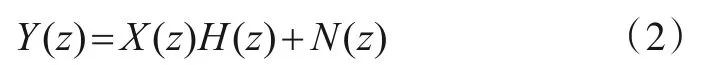
其中Y(Z)是接收波形的Z变换,X(Z)是发送波形的Z变换,H(Z)是水下声信道传输函数,通常认为它涉及各种水下衰减干扰,尤其是乘性噪声,N(Z)表示加性高斯白噪声.
由于水声信道是随时间、空间以及频率变化的信道,估计信道传输函数H(Z)是一个具有挑战性的工作.
实际上,在相干时间内,水声信道可被视为可确定的线性时不变滤波器或可确定的时空滤波器.因此,信道传输函数可以写成:

其中P表示信道在符号持续时间内的多径扩展条数,Ai和τi分别表示各径的幅度和时延,T表示采样周期表示舍入运算[14].
为了处理方便,在信道建模分析中,通常假定声速在水平方向上是不变的,根据深度将声速度水平分层化.在此基础上可近似推导出水声信号在信道中的声信号的能量分布、传播路线,减少建立水声信道模型的复杂度.
哈尔滨工程大学的艾宇慧等给出了几种典型海洋水声信道的传输函数,如下所示.其假设条件是水声通信带宽为5 kHz,采样频率为10 kHz[15].
声速为常数的均匀介质信道(Invariable Sound Velocity Gradient,ISVG)为:

负声速梯度信道(Negative Sound Velocity Gradient,ISVG)为:
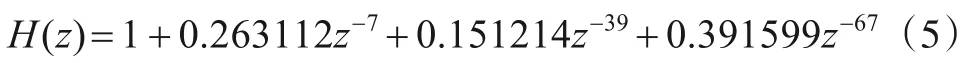
正声速梯度信道(Positive Negative Sound Velocity Gradient,ISVG)为:

5 极化码的构造
为了计算极化操作后各个子信道的可靠度,挑选出K位信息位索引,我们需要针对具体信道进行极化码的构造.目前的构造方法主要有BEC构造、信道退化构造以及蒙特卡洛构造[10]等,前两种方法分别适用于BEC信道和对称信道,然而水声信道环境复杂,为典型的非对称信道,因此本文采用具有普遍适用性的蒙特卡洛构造方法.
对于任意的B-DMC信道W,巴氏参数Z(W)表示为:

容易看出,Z(W)取值范围是[0,1].对于信道的容量I(W)有:
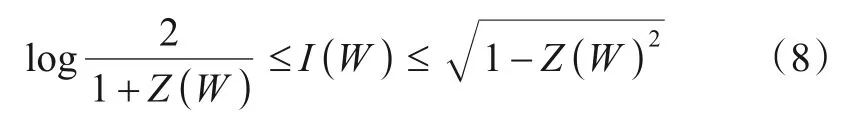
当信道容量I(W)=1的时候,巴氏参数Z(W)=0;反之,当I(W)=0时,Z(W)=1.因此,常常使用巴氏参数来表示信道的可靠度.
蒙特卡洛方法也称为统计模拟方法,是一种以概率统计理论为指导的非常重要的数值计算方法,其中心思想是用大量的实验频率统计替代概率.极化码的构造算法,即构造信道索引集合A,通过对极化操作后的子信道进行可靠度估计,然后从中选出可靠度最低的K个子信道用作传输信息位,其余子信道则传输冻结比特.用巴氏参数来表示信道的可靠度,从而:
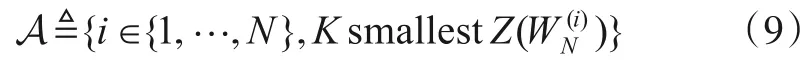
蒙特卡洛构造对应的算法是一种近似构造的算法,可以近似的模拟子信道的巴氏参数Z(WN(i))[10].由定义得:
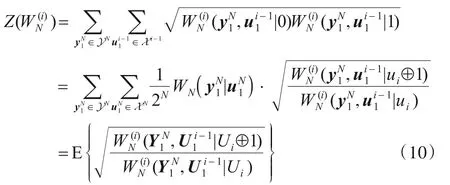
由前文建立的水声信道模型可知,基于射线声学原理上建立的多途传播模型是一种确定型信道模型,收发双方已知信道状态信息,在任意切分的块中,发送端和接收端都已知具体的衰落系数的数值.理论上,切块越小的情况下,信道模型越能反应真实的水下通信环境,此时hi是一个常数,假设噪声是服从均值为0,方差为δ2的正态分布随机变量.本文中的信道状态信息包括信道衰落因子h以及噪声的方差σ2,实际通信系统主要通过接收端的信道估计与无信号传输时噪声功率的测量得到h与σ2,随后通过通信反馈链路进行该信息的传递.
信号在发送端经过BPSK调制以后,信道的转移概率可以由如下公式计算:

此时,在每一个块中的初始似然比可以写成为:

实际计算过程常使用的是其以e为底的对数形式,其对数似然比(Logarithm Likelihood Rate,LLR)计算过程如下:
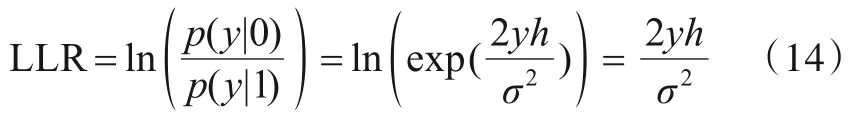
因此,蒙特卡洛构造极化码的算法可以表述如算法1.
值得一提的是,由于本次实验的仿真次数的数量级较大,为了确保实验过程可以顺利进行并如期得到实验结果,本次实验采用的仿真平台为Visual Studio 2015,分别对理论研究阶段的各个信道进行106到107次仿真,每个子信道分别仿真极化码的码长N为1024和2048,码率为0.5,最终冻结位索引集文件作为极化码构造阶段仿真结果的输出.

算法1蒙特卡洛构造极化码算法输入LLR(yi)输出 集合A步骤1:随机产生长度为N的码字uN1,通过调制后发送至已建立模型的水声信道,得到信道的输出yN1.步骤2:通过解调后,根据式(14)计算每个对数似然比信息LLR(yi),作为译码输入进行"精灵"辅助的SC译码,即在译每一个信息比特之前,在"精灵"辅助下该比特之前的信息比特都能正确译码.步骤3:统计多次传输和译码的结果,计算参数W(i)N(Y N 1,U i-11|Ui⊕1)W(i)N(Y N 1,U i-1 1|Ui)的均值,作为第i信道的可靠度参数Z(W(i)N).步骤4:排序挑选值最小的K个信道的索引构成集合A作为该信道信息位的遴选方案.
6 仿真结果分析
仿真实验结果表明极化码的纠错性能与码长、译码宽度都呈现正相关.为了与LDPC码作性能对比,码长为1024和2048的极化码分别与码长相近的1296与2304的LDPC码相比较.目前,CA-SCL算法是极化码性能最优的译码算法,其通过保留多条候选译码路径对传统的SC译码性能进行了性能的提升,候选路径的保留上限为译码宽度L,同时该算法在输出端辅以循环冗余校验,将第一条(可信度最高的路径)通过校验的译码路径作为译码结果,大大的提升了译码性能[11].因此,本文均采用CA-SCL算法作为极化码的译码算法,其中,码率设置为0.5,译码宽度设置为16,其中码长为1024的极化码的CRC校验长度设置为8,码长为2048的极化码的CRC校验长度设置为16;LDPC码均采用置信传播(Belief Propagation,BP)译码算法,最大迭代次数设置为30次,本次仿真实验所使用的调制方式为BPSK.
图3~5分别展示了在ISVG、NSVG和PSVG信道下,不同码长的极化码和LDPC码的仿真性能对比.从仿真结果可以得到以下的结论:在三种信道下,对于极化码和LDPC码,译码方式一旦给定,性能就与码长长度呈现正相关,即码长越长,性能越好;在ISVG信道下,码长为1024和2048的极化码分别在信噪比约为2.0 dB和3.1 dB时性能开始超越LDPC码;在误码率要求为10-4量级时,码长为1024的极化码可以多提供大约0.5 dB的编码增益,综合来看,在ISVG信道中,极化码的性能要优于LDPC码,提高信噪比时,极化码性能曲线下降越来越陡峭,即信噪比提高时极化码可以获得更高的性能收益.在NSVG信道下,码长为1024的极化码整体性能不如码长为1296的LDPC码;码长增加到2048以后,此时译码宽度为16,CRC长度也增加到16,性能曲线下降速度很快,在大约1.7 dB时可以超越LDPC码,并且呈现越来越陡峭的趋势;在误码率要求为3×10-6时,码长为2048的极化码可以比码长为2304的LDPC码多提供约0.5 dB的编码增益.在PSVG信道下,在信噪比大约在0到3.5 dB区间内,码长为1024的极化码的性能比码长为1296的LDPC码性能优越;当信噪比大于1.5 dB时,码长为2048的极化码明显优于码长为2304的LDPC码,并且误码率下降趋势很快;整体来看,在低于水声通信性能指标10-4的情况下,码长为2048的极化码优势较为明显.
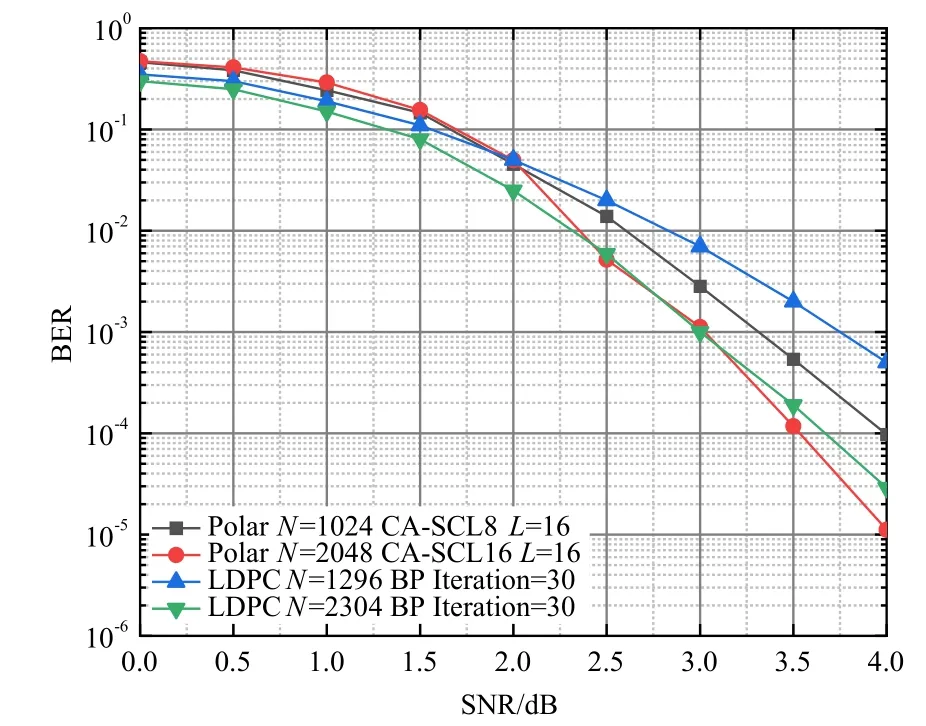
图3 ISVG信道下的性能仿真
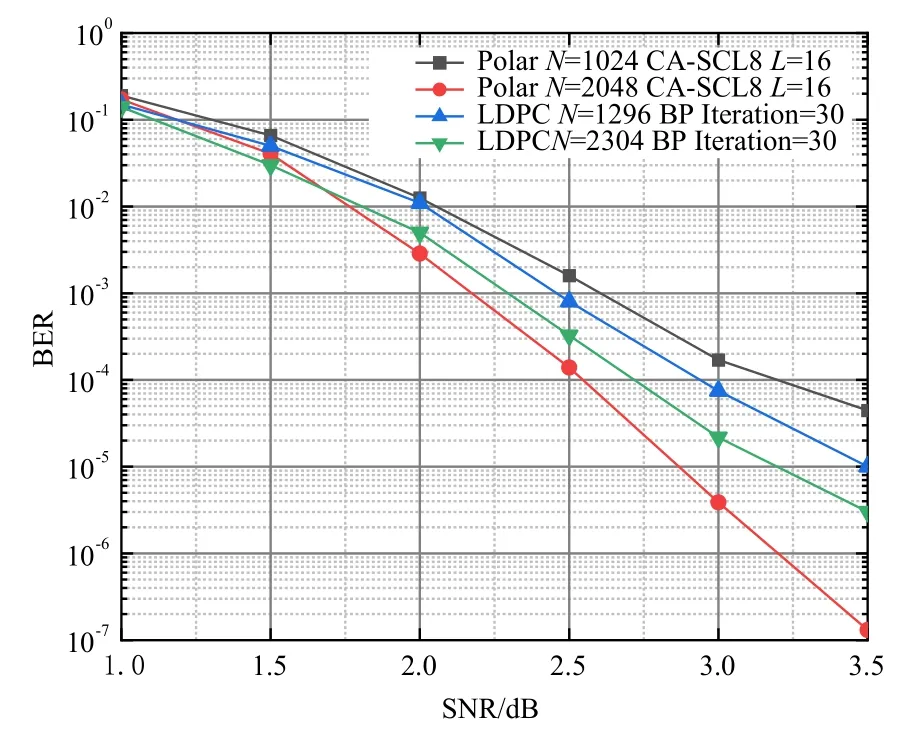
图4 NSVG信道下的性能仿真
我们进一步比较了极化码同LDPC码的编码复杂度.令码字长度为N,对于给定校验矩阵的LDPC码,编码过程需要进行高斯消去和矩阵乘法,所需要的复杂度分别为O(N3)和O(N2),因此LDPC码的一般编码复杂度为O(N3).极化码具有清晰地编译码结构,由于其递归结构,编码可以在编码因子图上进行,需要进行模2加法和反转操作,其所需编码复杂度为O(NlogN)[10].因此,与LDPC码相比,极化码编码结构清晰简单,且编码复杂度更低.

图5 PSVG信道下的性能仿真图
7 结论
为保证水声数据的可靠传输,提高时-频-空域动态变化范围大的水声信道的纠错性能、信号功率等综合利用效率,本文提出将极化码应用于信道环境恶劣的水声信道,并使用蒙特卡洛构造作为极化码的构造方法,CA-SCL作为其译码算法.仿真结果展示了在不同信道环境下不同码长、以及不同译码方式下构造的极化码纠错性能的对比,其中信道传递函数分别为ISVG、NSVG和PSVG,整合三种信道下极化码和LDPC码的仿真结果,整体呈现出码长越长性能越好的特点;在三种信道下,极化码纠错性能的表现都较为突出尤其在PSVG信道下,在低于水声通信性能指标10-4的情况下,码长为2048的极化码相对于LDPC码的优势明显;除了在NSVG信道下,码长为1296的LDPC码相较于1024的极化码有一定优势外,其余情况下极化码整体的综合性能要优于相近码长的LDPC码且极化码的性能下降速度更快.综合以上,可以看出与LDPC码相比,在同等信噪比条件下,极化码在水声通信系统中,拥有更好的纠错性能,在提高信噪比时可以获得更高的编码增益,具有很强的竞争力.在实际应用场景中的信道编码方案的遴选工作中,可以根据误码率、信号功率等具体需求,平衡其性能与计算复杂度,挑选出与硬件更为匹配的信道编码方案.

