一种基于改进PSO优化的LSTM航迹预测模型*

韩 超

（海装沈阳局驻大连地区第一军事代表室 大连 116000）

1 引言

雷达航迹预测是雷达目标跟踪的关键环节，其主要目的是利用目标航空器的历史航迹数据，预估其未来轨迹。随着战场环境日益复杂和干扰技术的快速发展，对敌对目标的航迹预测需要面对更多的干扰因素，由此带来的误差问题对雷达机动航迹预测提出了日益严峻的考验。

目前关于飞行器的短期预测算法大致可分为两类。其中一类方法为传统机器学习，运用卡尔曼滤波算法对观测数据进行最小二乘估计，使用诸如卡尔曼滤波算法［1］、竞争神经网络［2］、支持量机［3］、灰色模型结合马尔科夫链［4］等方法对飞行器的航迹进行处理，并给出轨迹预测。此类方法的缺陷是较为明显的，那就是依赖专家知识搭建目标飞行器的动力学方程，无法进行实时预测，且易受到外部环境因素的影响。另一类方法为神经网络算法的若干变种［5］，相较于上面一类算法，它们具备用时短、通用性强等特点，能够满足对飞行器轨迹预测的实时、高效的要求，但针对复杂的海面飞行器轨迹预测问题，神经网络的映射表达能力有限，参数难以调整，且在本质上算法更容易使得损失函数的训练结果落入局部最优点而不是全局最优点，且无法针对时间序列上的变化进行建模。

本文充分结合PSO算法和LSTM网络的设计思想，以PSO优化实现LSTM航迹预测网络在训练中的自动调参，通过对LSTM超参数的全局寻优，实现航迹预测效果的提升。

2 LSTM单元构造方法

定义1若一个递归神经网络隐藏层单元具备如下特征，则称该单元为LSTM单元。

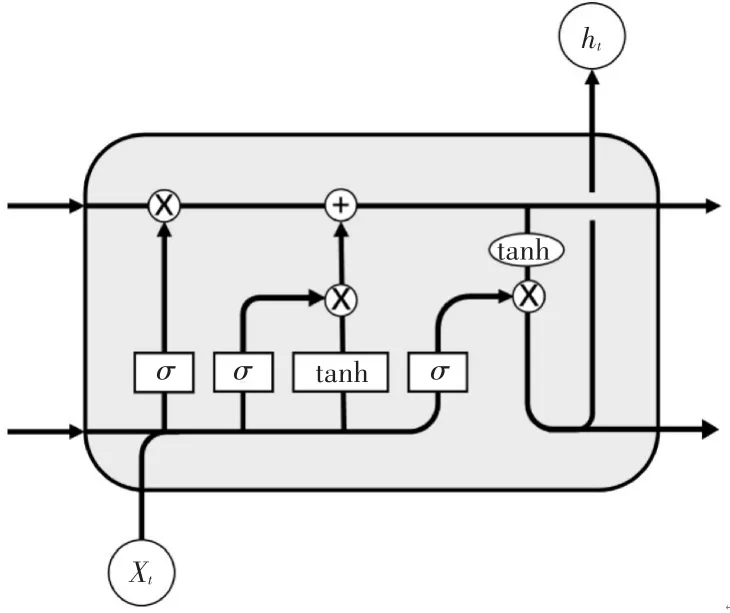
图1 LSTM隐藏层单元结构图

其中，it为输入门，ot为输出门，ft为遗忘门；ht-1为t-1时刻隐藏层状态，ht为t时刻隐藏层状态；xt为t时刻输入层状态；σ为Sigmoid函数，tanh为双曲正切函数，Ct为t时刻单元状态；Ct-1为t-1时刻单元状态；为记忆单元的输入状态。算法的执行步骤如下。

步骤1利用遗忘门筛选ht-1和xt信息

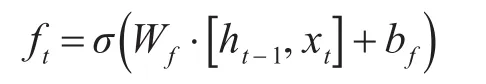
式中，bf为遗忘门的偏置项。

步骤2利用输入门确定此时须更新的数值和即将加入的新单元状态

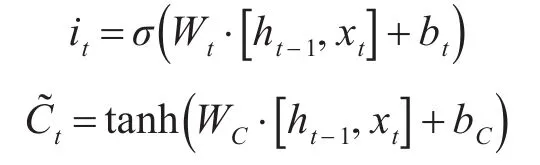
式中，bt，bC为输入门的偏置项；Wt，WC为输入门权重。

步骤3综合输入门和遗忘门的信息计算单元状态Ct：

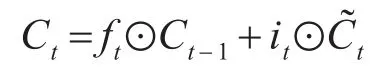
步骤4利用输出门，将Ct传递给激活函数获得最终输出：

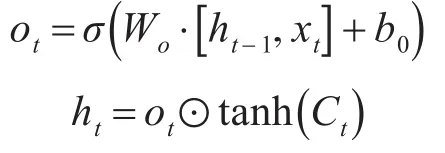
3 PSO优化算法原理

PSO算法是一种对多维搜索空间内最优解的搜寻算法。其核心原理是在空间内维持一定数量的粒子，每个粒子均代表问题的一个可能解，包含位置、速度和适应度三项指标。粒子在解空间内移动，并通过粒子间信息交互，不断迭代寻找较优区域，从而实现在整个解空间内的最优化过程。

PSO算法的实现步骤如图2所示。

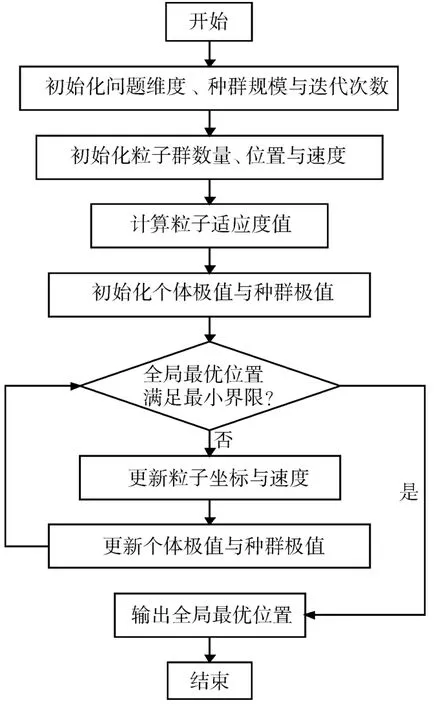
图2 PSO算法流程图

步骤1初始化粒子群参数。设目标粒子群位于D维解空间中，包含N个粒子，个体历史最优适应度值为fp，种群历史最优适应度值为fg，则有初始粒子群参数如下所示。

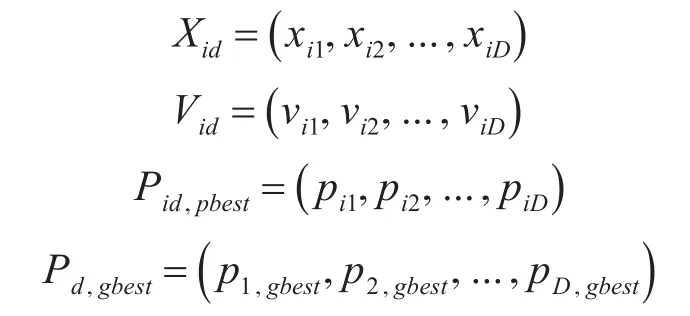
式中，Xid和Vid为第i个粒子的位置与速度；Pid，pbest为个体最优解；Pd，gbest为种群最优解。

步骤2若全局最优位置满足最小界限，则输出全局最优位置并结束，否则执行步骤3。

步骤3对粒子速度进行迭代更新。

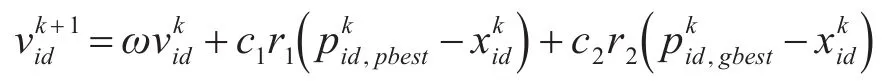
式中，ω为惯性权重，表征了粒子维持当前运动趋势，在全局与局部极值间的平衡；c1和c2为学习因子，用于调整粒子向自身与全局最优值前进的步长；r1和r2为满足[0，1]间均匀分布的随机数。

步骤4对粒子位置进行迭代更新。

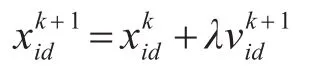
式中，λ为速度系数。

步骤5根据步骤3与步骤4中的结果，对比历史个体最优位置与全局最优位置，若较好，则将其保存为个体最优位置或全局最优位置，并跳转至步骤2。

4 本文算法设计

4.1 基于自适应权重的PSO算法

经典的PSO算法在解空间寻优过程中可能会出现容易陷入局部极值、搜索精度低等问题。为了加快收敛速度、避免陷入局部最优值，本文构建了惯性权重与学习因子的动态变化公式，将固定参数转换为非线性变换参数，以改善收敛的精度和速度。

步骤1惯性权重ω的自适应改进。惯性参数决定了粒子的历史飞行状态对当前飞行速度的影响力，对于在局部寻优与全局寻优间取得均衡具有重要意义。惯性权重应当与粒子种群状态有关：在寻优的初期，应当尽可能扩张每个粒子的搜索空间；在寻优后期，应当逐步收敛至适应度值较好的区域，并进行精细搜索。其表达式为

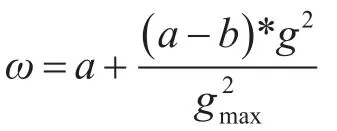
式中，g为当前的迭代次数；a为惯性权重的最大值值，b为惯性权重的最小值；gmax代表迭代次数的最大值。

步骤2学习因子c1和c2的自适应改进。其中，是粒子自我认知的体现，用于对粒子自身知识进行总结；是粒子社会认知的体现，用于向表现更好的粒子学习；在寻优初期，我们需要关注个体自我认识的能力，而后期则应注重个体获取社会信息的能力。由此其表达式为

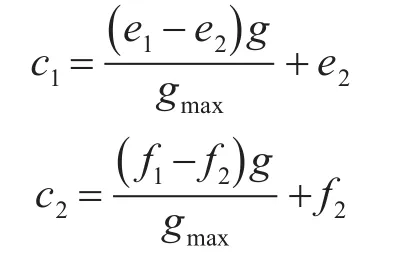
式中，g为当前迭代次数；gmax为最大迭代次数；e1和f1取值1，e2和f2取值2。

4.2 Dropout正则化

由于航迹数据在微观上具备小幅震荡特征。在这样的前提下，如果LSTM模型的参数过多而训练样本不足时（这种情况极为常见），会诱发过拟合现象，表现为航迹图像上的毛刺与震荡，泛化性和准确性变差。为了解决这一问题，我们在LSTM模型中引入Dropout正则化层，其核心思想是在每轮训练中令随机部分LSTM单元暂时失活，使模型不再依赖于部分节点之间的耦合作用，如图3所示。

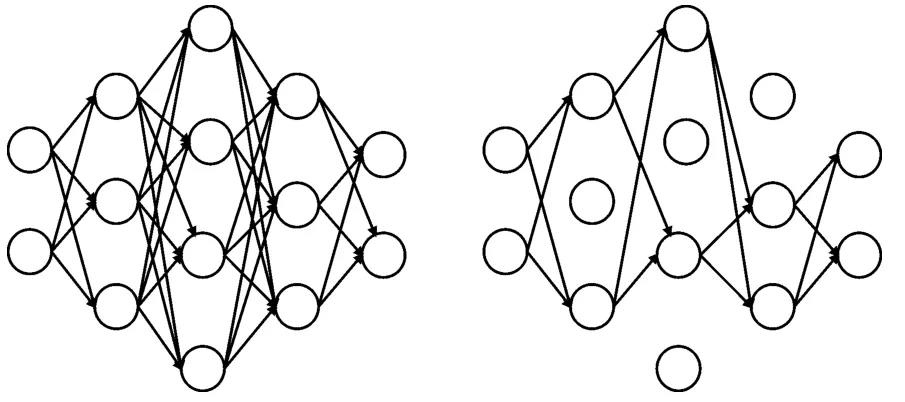
图3 PSO算法流程图

Dropout层的算法步骤如下。

步骤1利用伯努利法设置激活概率ρ。设网络的激活函数为Sigmoid函数，输入为X=[x1，...，xm]，单元初始权重为W=[ω1，...，ωm]，则LSTM单元的激活值如下式所示。

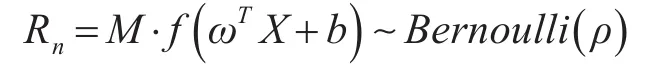
式中，M为服从伯努利分布的掩模矩阵，其中每个元素为1的概率为ρ；b为偏置值。

步骤2通过ρ备份并删除BiSRU网络隐藏层中的部分单元，并进行本轮训练。

步骤3恢复在步骤2中删除的BiSRU网络隐藏层单元。转至步骤2，直至所有数据训练完成。

4.3 基于PSO优化的LSTM模型

将基于自适应权重的PSO算法与LSTM算法进行结合，构建组合模型，如图4所示。设目标飞行器第k个雷达航迹点特征Fk坐标输入该模型的格式为

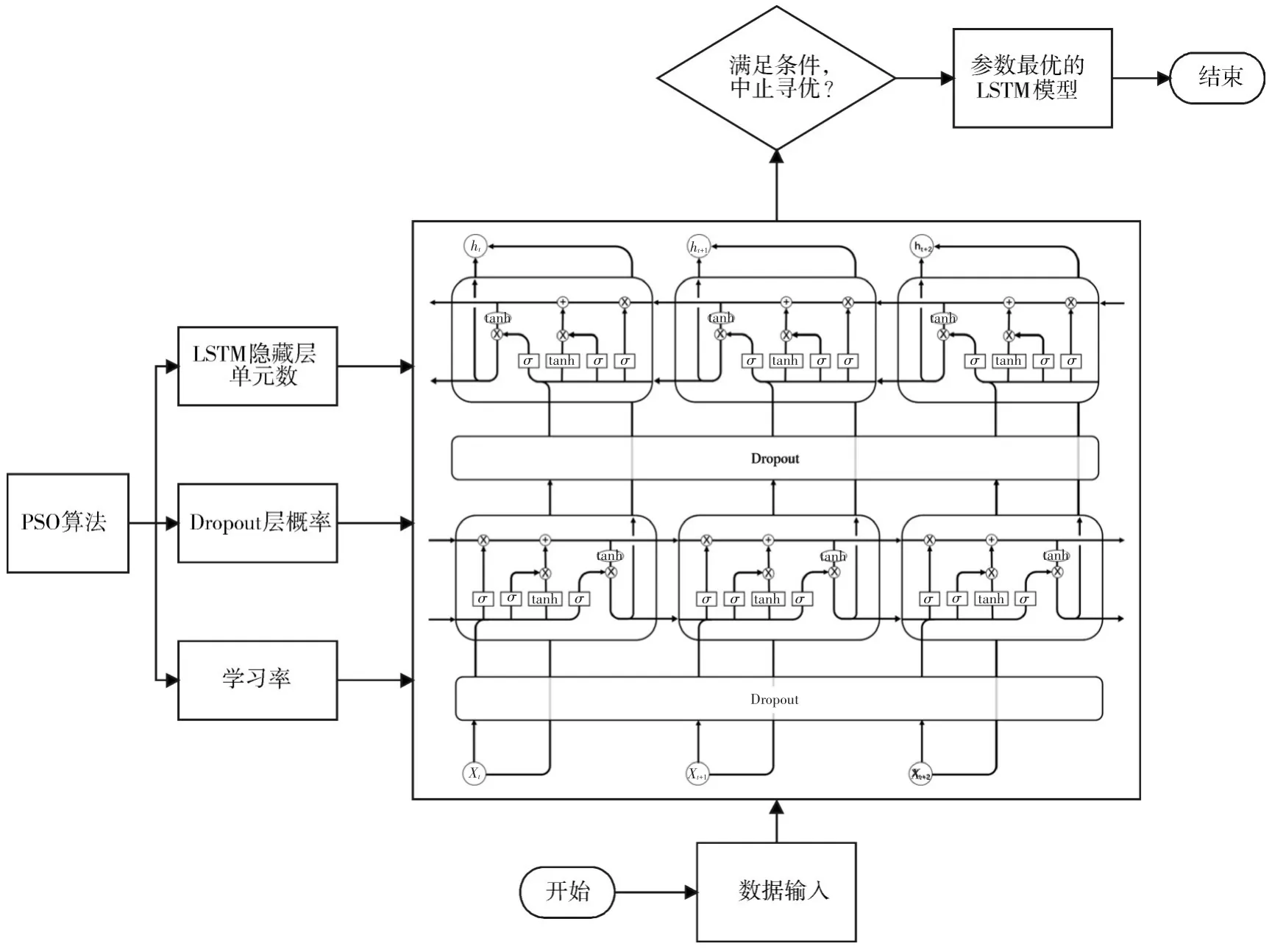
图4 PSO-LSTM模型结构图

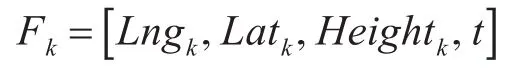
式中：Lngk为当前时刻点的经度，Latk为当前时刻点的纬度，Heightk为当前时刻点的高度，t为当前时刻时间。

步骤1航迹数据预处理。包括坐标系转换、重复航迹点剔除、缺失航迹点填充、异常值处理等步骤，并按7：3的比例切割为训练集与预测集。

步骤2初始化粒子种群X。设置粒子群种群规模、迭代次数、初始速度与位置区间。

步骤3初始化粒子速度、位置。随机产生一个X中粒子xi，0(α，ε，ρ)，其中，(α，ε，ρ)为粒子群的寻优参数，α为LSTM层的隐藏层单元数；ε为学习率；ρ为Dropout层丢弃概率。

步骤4设置本文模型的误差指标为适应度值，包含均方根误差（Root Mean Square Error，RMSE）与平均绝对值误差（Mean Absolute Error，MAE）两种指标。其中，RMSE通常表示为真实值与预测值偏差值的标准差；MAE是绝对误差的平均值，通常表示为偏差在样本上的均值。对两种指标的定义如下。

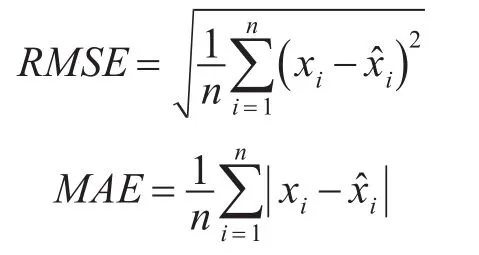
式中，n为航迹数据集内样本点数量；xi为第i个航迹样本点的实际值；为第i个航迹样本点的预测值。

步骤5根据适应度值变化，更新单个粒子的个体最优位置与全局最优位置，并更新自身的位置坐标与速度。

步骤6粒子群迭代更新，直至适应度值RMSE与MAE趋于稳定，并确定寻优参数(α，ε，ρ)数值。

步骤7将最优参数输入至LSTM网络，训练并进行预测。

5 仿真验证与分析

5.1 实验数据

为了证明模型的有效性，仿真实验在某型多源信息融合系统仿真平台上完成。我们选择雷达数据集中的5000个包含正常值和异常值的连续航迹数据流进行预测。并使用BP神经网络、FC-LSTM算法与本文的PSO-LSTM算法进行对比实验。

5.2 实验结果分析

PSO-LSTM航迹预测模型初始参数设置如表1所示，寻优参数范围设置如表2所示。

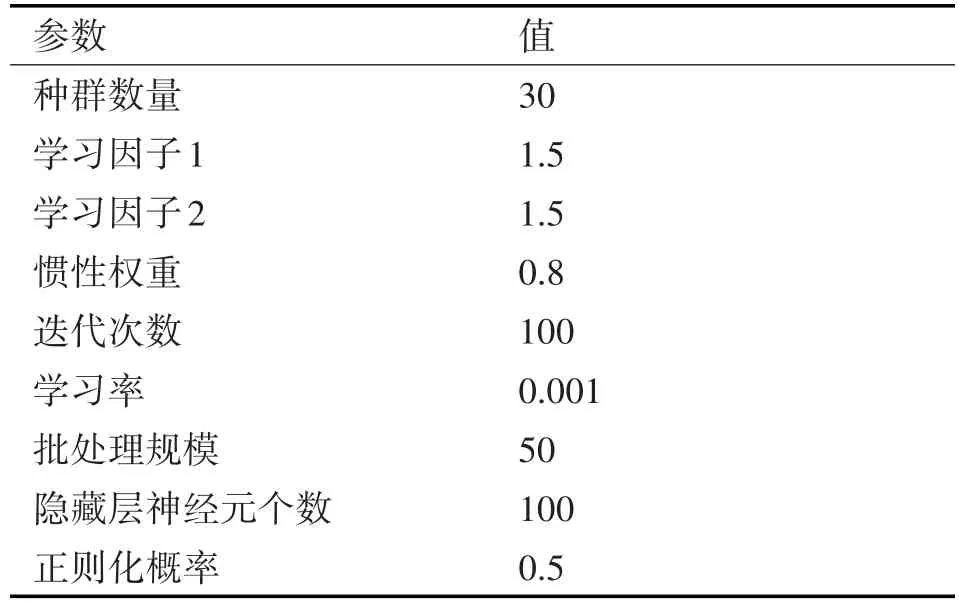
表1 PSO-LSTM初始参数设置

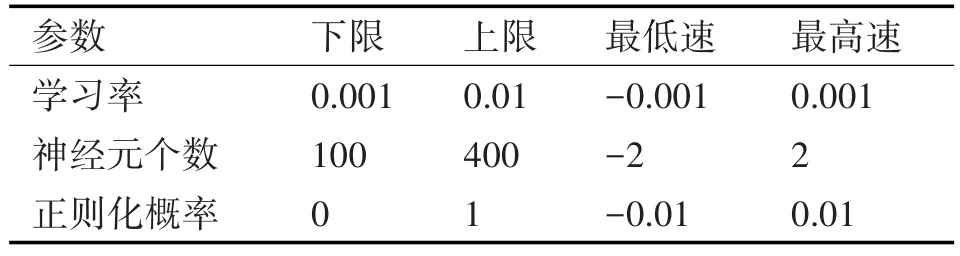
表2 PSO-LSTM寻优参数范围设置

由图5（a）可见，适应度值在26次迭代后趋于稳定，可得到最优解；由图5（b）可见，LSTM隐藏层神经元单元数量同样在26次迭代后稳定，最优神经元数量为25；由图5（c）可见，学习率在11次迭代后趋于稳定，最优学习率为0.0087；由图5（d）可见，Dropout层概率在40次迭代后趋于稳定，最优概率为0.45。

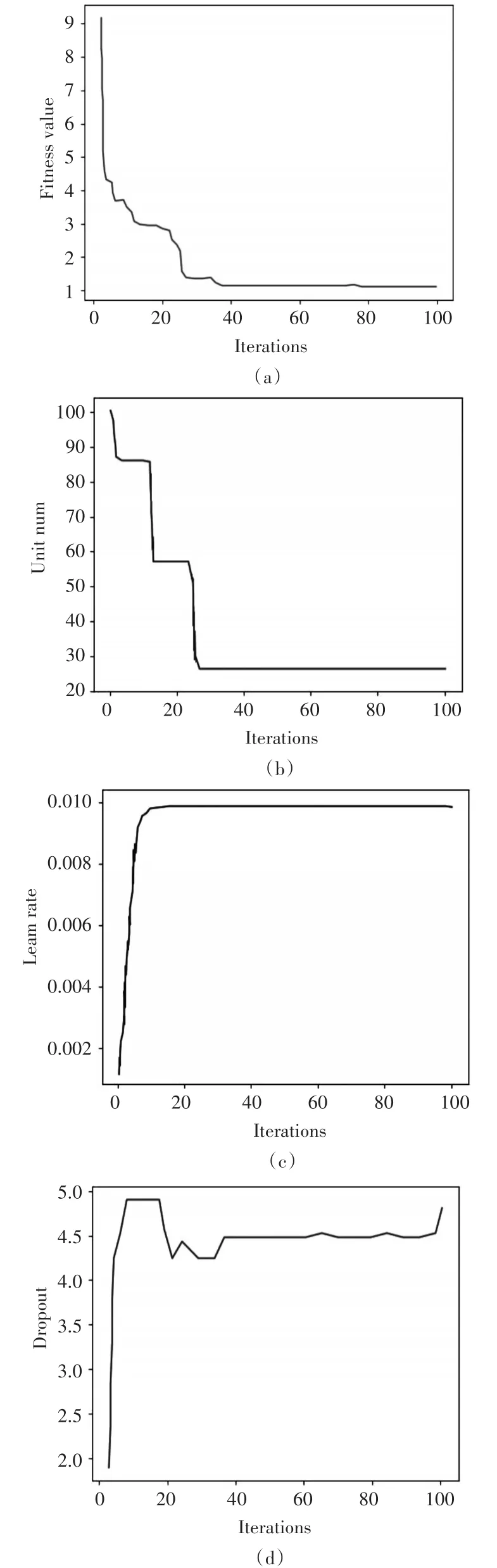
图5 PSO优化超参数变化曲线

由图6与表3所示，PSO-LSTM航迹预测模型的RMSE为5.953121，相对于FC-LSTM模型降低了0.32，相对于BP模型降低了3.47；PSO-LSTM模型的MAE为4.841432，相对于FC-LSTM模型降低了0.65，相对于BP模型降低了3.06。说明PSO-LSTM模型相对于传统算法改进了寻优能力，在预测精准度与准确性上有所提升。

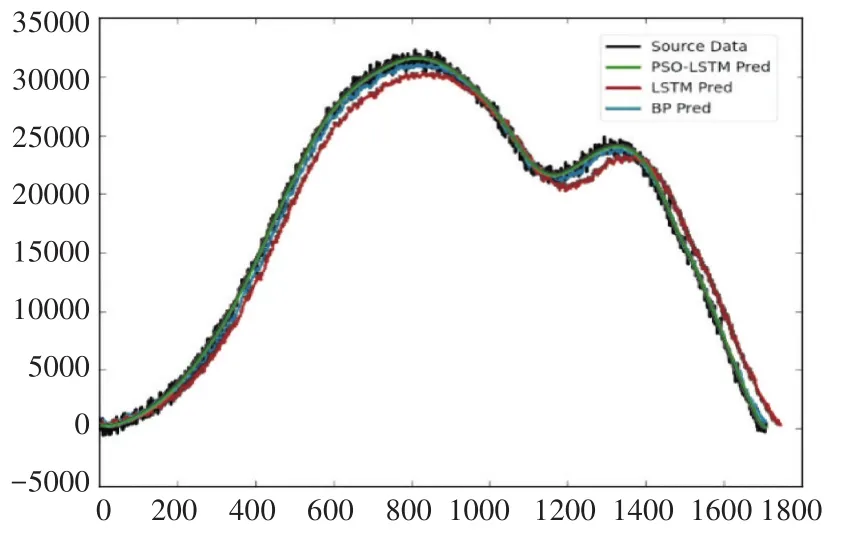
图6 航迹预测效果图

表3 不同预测模型评估指标

本实验使用的计算机配置为AMD Ryzen 7 3700X8-Core Processor 3.60 GHz，Windows操作系统。实验数据为人工生成，实验使用Python语言在Pytorch平台下训练。

6 结语

本文提出了一种基于改进PSO优化的LSTM航迹预测模型，利用PSO算法解决了LSTM网络的自动参数寻优问题，能够降低人为因素对网络的干扰，高效地实现重要超参数的自动调整。使用某飞行器数据进行实验，本文模型相对传统模型的RMSE与MAE值均有下降，证明了本文方法的有效性。