偏心量影响下的松动故障转子非线性分析

刘桂珍，马晓君，李小海，袁聪聪，闻邦椿

（1.佳木斯大学机械工程学院，黑龙江 佳木斯 154007；2.东北大学机械工程与自动化学院，辽宁 沈阳 110819）

支座松动故障是旋转机械中危害较大的一种常见故障［1］。旋转机械长期在高转速下运行，旋转所产生的离心力以及各种不平衡力大于其所受重力，会导致轴承支座和基础之间在垂直方向发生分离。质量偏心是转子系统运转时产生不平衡力的主要来源，会引起机器振动、影响转子正常运作，甚至会产生严重事故的重要因素之一［2-3］。因此，研究偏心量对具有支座松动故障转子系统的响应具有重要的意义。

目前国内外学者对松动故障的研究，都是在分段线性力学模型基础上进行的。Ma等［4］利用有限元法，分析了有关参数对松动故障的动态响应；蒋兆远等［5］分析了横向流体激振力，对松动故障支座质量的非线性动力学影响；芮品先［6］研究了有界噪声激励下的松动故障转子，进入分岔与混沌的演变过程；张靖等［7］发现两端均有松动故障的转子系统，支座位移不同，会导致系统响应的频谱特征发生显著变化；于欢［8］研究表明，受支承刚度阶跃影响，支承松动转子系统会产生混沌运动；曹树谦［9］针对一端支承松动的转子系统，利用遗传算法，对松动端的故障非线性参数进行识别；黄亚明［10］利用数值求解，分析出松动故障的一般特征；伍小莉［11］分析了松动故障的转子系统，超过临界转速后，偏心量的增加，会激起系统强烈的振动；李宏坤等［12］结合转轴材料的非线性，得出支座松动故障频谱图以低频为主、高频部分响应幅值相对较小的结论；刘杨等［13］研究发现，滑动轴承支撑下的松动-碰摩耦合故障，通常以碰摩故障特征为主，时域波形呈现下密上疏的波动形状，轴心轨迹表现为多个嵌套的“半椭圆形”，这些故障特征可以作为诊断滑动轴承（油膜力）支撑下松动-碰摩耦合故障的一个理论依据。

本文以转子系统具有支座松动故障为研究背景，利用拉格朗日方程，建立了非稳态油膜力作用下的转子-定子-轴承系统松动故障的6质量、12自由度的非线性动力学模型，应用数值分析，研究了当偏心量作为唯一控制参数时转子系统的响应，所得结论为该类转子的故障诊断和系统的安全运行提供理论依据。

1 力学模型与微分方程

1.1 拉格朗日方程描述

设有n个质点组成的质点系，受完整的理想约束，具有N个自由度，其位置可由N个广义坐标方程来确定。则有

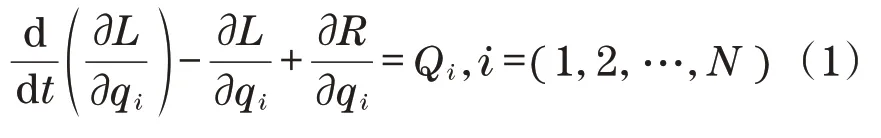
式中：L为拉格朗日函数，L=T-V（T为系统的动能函数，V为系统的势能函数）；R为与系统阻尼相对应的耗散函数；Qi为作用在系统上的广义力；qi为系统独立的广义坐标；N为系统的总自由度个数。

1.2 非稳态油膜力模型［14］

非线性油膜力模型采用短轴承假设下的Capone非线性油膜力模型，该模型有较好的精度和收敛性。在短轴承油膜力假设条件下的无量纲雷诺方程为

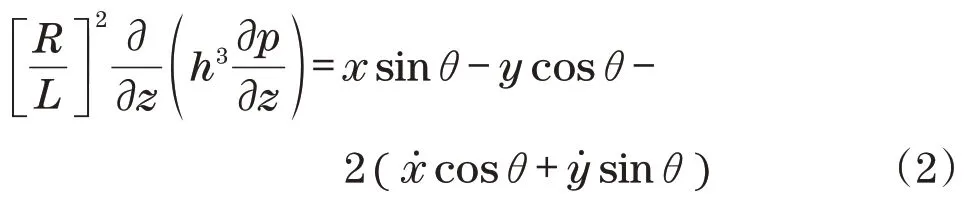
式中：h为无量纲油膜厚度，h=为油膜厚度，C为轴承径向间隙）；z为无量纲轴向位移，z=（为轴向位移）；p为无量纲油膜压力，p=为油膜压力，μ为油膜黏性系数；x、y分别为无量纲轴颈中心x、y方向的位移分别为无量纲轴颈中心x、y方向上的速度分量。

由式（2）可得无量纲油膜压力为

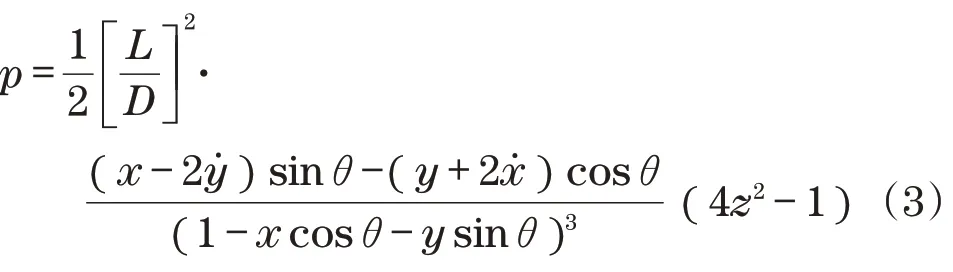
式中：D为轴承直径。

无量纲非线性油膜力最终可以表示为

式中：

1.3 力学模型

带有两端支座松动故障的转子-定子-轴承系统如图1所示。假定系统中两端支座同时出现松动，轴颈两端由相同的油膜轴承支撑，设δ为轴颈与轴承间的平均间隙，O1为转盘的几何中心，Oc为转盘的质心，O2、O3分别为两端轴颈的几何中心，O4、O5分别为两端轴承的几何中心，m1为转盘处的等效集中质量，两端轴承支座质量相等，即m2=m6，两端轴颈在轴承处的等效集中质量相等，即m4=m5，定子支座质量为m3。

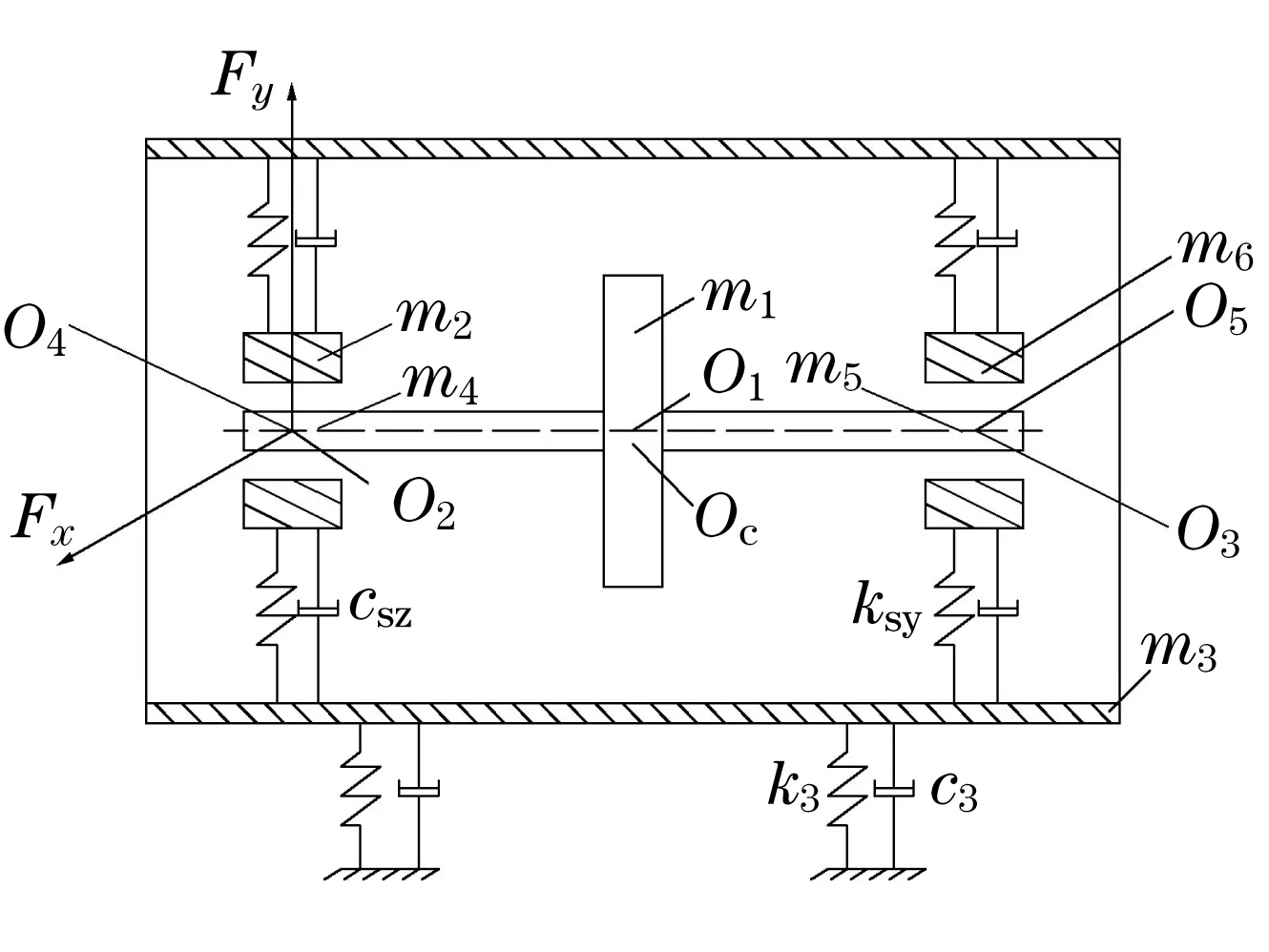
图1 转子-定子-轴承系统松动故障的动力学模型Fig.1 The dynamics model of rotor-stator-bearing system with looseness fault

假设圆盘与轴颈之间为无质量弹性轴，k1为转轴刚度系数，k2为轴承支撑刚度系数，k3为定子基础刚度系数，kr为轴承座与基础之间的等效刚度，ksz、ksy分别为松动端左、右轴承座的分段刚度，单位为N·m-1；c1为转轴阻尼系数，c2为轴承支撑处的结构阻尼系数，c3为基础对定子的阻尼系数，csz、csy分别为松动端左、右轴承座的分段阻尼，单位为N·s·m-1。

1.4 运动微分方程

设盘心O1和轴颈中心O2、O3的位移分别为（x1，y1）、（x2，y2）、（x6，y6），ω为轴的转动角速度，e为不平衡量，μ为油黏度，R为轴颈半径，L为轴颈长，Fxz、Fyz和Fxy、Fyy分别为左、右两端轴承受到的油膜力。

根据拉格朗日方程，对图1建立具有两端松动故障的转子-定子-轴承系统的质点运动微分方程组（̈为位移x、y的二阶导数加速度）：

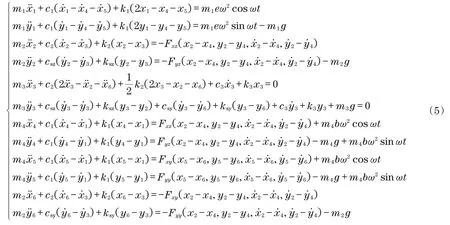
当松动发生时，设松动的最大无量纲间隙值为δ1，分段线性表示为

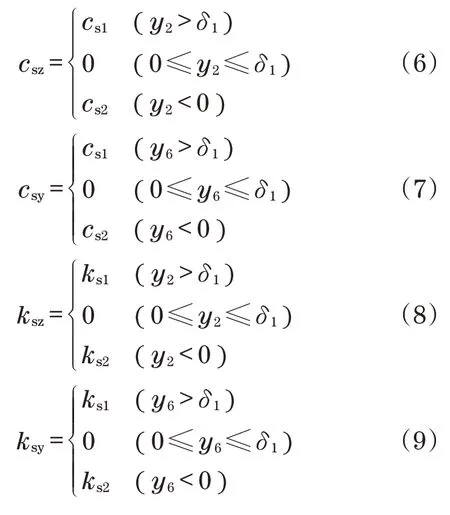
2 数值模拟

运用4阶Runge-Kutta法对数值进行求解，在计算中为了能够较快得到稳定解，应将步长选得尽量小且周期足够多。

为了保证解的收敛性并减小计算误差，计算中需要选用较小的时间步长，同时为了能记录到振动的稳定解和消除瞬态响应的影响，略去前2 000个数据点，取后4 500个数据点。计算轨迹图时取10～20个周期。设系统的参数为m1=4.0 kg，m2=m6=32.1 kg，m3=50.0 kg，m4=m5=20.0 kg；R=25 mm，δ2=0.2 mm，e=0.1 mm，μ=0.018 Pa·s，c1=1 050 N·s·m-1，c2=2 100 N·s·m-1，c3=2 100 N·s·m-1；k1=2.5×105N/m，k2=2.5×105N/m，k3=2.5×107N/m，ks1z=1.0×106N/m，ks2z=20.0×106N/m，ks1y=5.0×106N/m，ks2y=10.0×106N/m；cs1z=1 500 N·s/m，cs2z=1 500 N·s/m，cs1y=1 500 N·s/m，cs2y=1 500 N·s/m，δ1z=0.01 mm，δ1y=0.01 mm，轴承有效长度L=12 mm。

图2描述的左、右松动支座在不同偏心量下随激励频率变化的分岔图。观察图2结合此时的庞加莱截面图，得出转子系统在偏心量b=0.5 mm时的动态响应为周期运动→混沌运动→周期运动→P-3运动→周期运动→混沌运动。

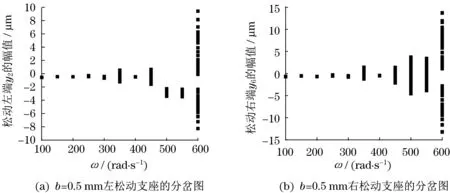
图2 左、右松动支座在偏心量b=0.5 mm时随激励频率变化的分岔图Fig 2 The bifurcation diagrams of left and right loose bearing with excitating frequency changing when b=0.5 mm

图3所示为偏心量b=0.5 mm、激励频率ω=350 rad/s时转子系统响应，此时转子系统处于P-3周期运动。观察此时系统响应，可清晰地表明，时域波形图由多种频率成分组合，形成3个大小不等的“M”形波峰，并且具有明显的“削波”现象；轴心轨迹出现3个纠结在一起、形成有立体趋势不规则的环状结构；幅频曲线形成连续图谱，幅值谱上以2/3倍频、1倍频为主，同时生成差分较小的高倍分数频谱，形成连续曲线的次谐波组合。

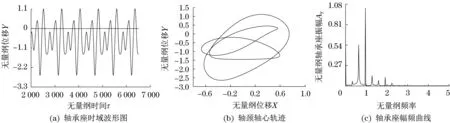
图3 偏心量b=0.5 mm、激励频率ω=350 rad/s时转子系统的响应Fig.3 The response of the rotor system when b=0.5 mm，ω=350 rad/s

3 结论

通过偏心量对松动故障转子系统响应的运动特性研究，得出以下结论：①系统呈现出周期运动、拟周期运动、混沌运动等多种形式的运动；②能够同时产生低次谐波和2倍等高次谐波的振动分量；③系统出现明显的“削波”现象，频谱成分多以低频为主、伴随幅值较小的高频成分；④相轨迹呈现出特殊的形状，可为有效识别支座松动故障的转子系统提供理论依据。