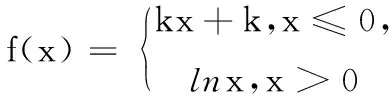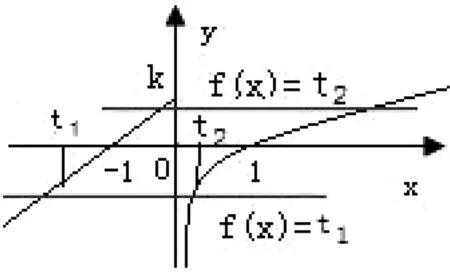几类复合函数典型问题的解法探究

安徽省利辛县第十中学 (236700) 孙 标

近年来，高考对复合函数的考查力度有加大趋势，随之对应的模拟题也不断涌现，本文中介绍的复合函数就是几个典型的题例，供参考．

一、复合函数的求值

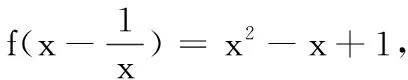
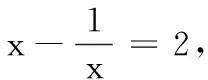
点评：有一些复合函数很难化为普通函数，此时关于他们的求值问题，我们可以逆向思维，如本例的方法建立方程解题，这里要注意多值情况的分类与统一．

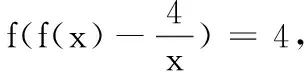
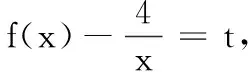
点评：本题虽然也是求函数值的问题，但如果直接代入得f(f(4)-1)=4，往下就无路可走了，故而需审视问题特点，抓住解决复合函数问题的规则，通过换元将题目转化为我们熟悉的一阶函数题.

二、解复合函数方程或不等式

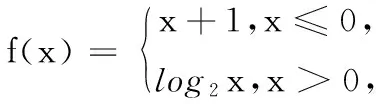
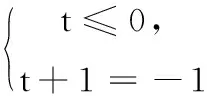
点评：本题实质是解方程类型的问题，通过换元后分层解两个方程使问题获得顺利解决，关注中间变量范围的变化是正确解题的重要因素.

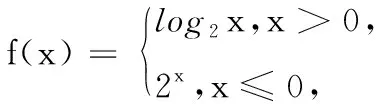
析解：当x≤0时，f(x)=2x∈(0,1]，则f(f(x))=log22x=x，不等式即x>1，与x≤0不合；当01，也不合题意；当x>1时，f(x)=log2x∈(0,+∞)，则f(f(x))=log2(log2x)，不等式即log2(log2x)>1，得x∈(4,+∞)．

点评：本题通过分类讨论可以把具体的函数表达式写出来，这样就能顺利解不等式了，这是解此类题的常规方法，如果不能直接表示出来，可采用换元法(如前例)分层求解．

三、求复合函数中的参数最值或范围

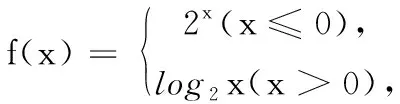
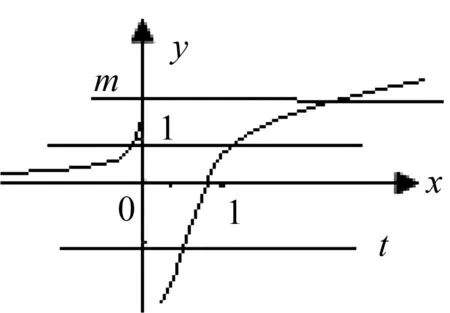
图1

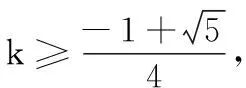
点评：本题通过设m=k2y2+ky，把问题转化为方程f(f(x))=m有一个解的问题，然后再寻找此复合函数方程有一个解的条件，再用前面解方程的方法可以达到解题目的．

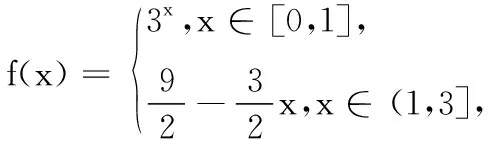
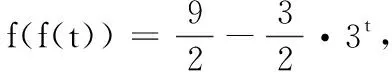
点评：本题实际上是已知函数值域求其定义域的问题，通过分段讨论得到函数表达式是最基本的方法，也可用换元法(如前面)分步求解．

四、复合函数的零点问题

例7 若函数f(x)=x3+ax2+bx+c有极值点x1,x2，且f(x1)=x1，则关于x的方程3(f(x))2+2bf(x)+b=0的不同实数根是.

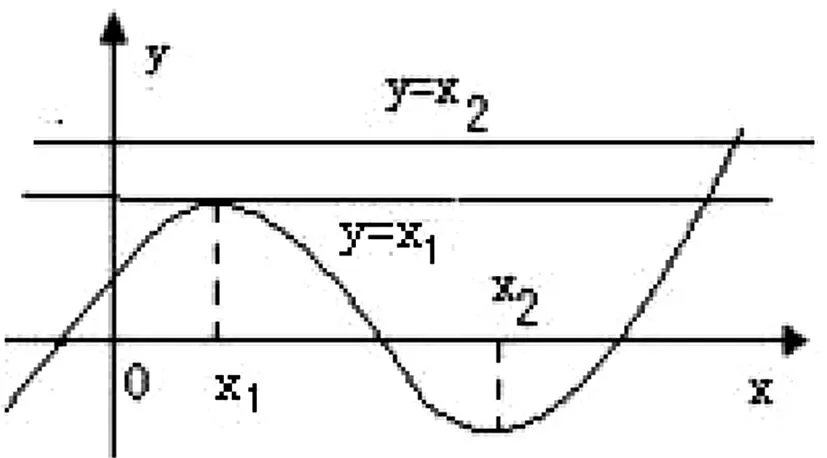
图2

析解：由于f′(x)=3x2+2ax+b，则方程3(f(x))2+2bf(x)+b=0就是f′(f(x))=0，令f(x)=t，则原方程变为f′(t)=0，因为函数有两个极值点x1,x2，即f′(t)=0有两个根t=x1,t=x2，所以解两个方程f(x)=x1，f(x)=x2的根就是原方程的根.画出三个函数y=f(x),y=x1,y=x2的图象如图2，设x1

点评：本题是一个关于导函数的复合函数，通过换元并设出两个极值点x1,x2，就将原方程转化为两个函数的零点问题，再根据条件f(x1)=x1画出符合题意的函数关系图，得到了原方程解的情况．

图3

点评：本题是根据函数零点的个数来确定参数范围，通过换元并分层利用分段函数图象和特点分析就能比较容易地解决问题．