两道圆锥曲线高考题结论的再推广

安徽省砀山中学 (235300) 蔡 聪

在文[2]中，笔者以2020年高考数学全国卷Ⅰ理科第20题和2020年高考数学山东卷第22题为例，介绍了齐次化方法在解决圆锥曲线中关于斜率之和为定值或斜率之积为定值的问题中的应用，并借助于齐次化方法将两道题的结果在椭圆的模型中推广出一般的结论，考虑到圆锥曲线性质的相似性，笔者继续在双曲线和抛物线中，探究出以下结论，与同仁交流.

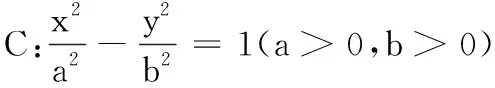
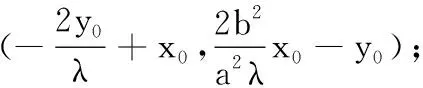
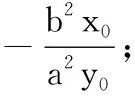
(3)当λ=0且y0=0时，直线AB的斜率不存在.

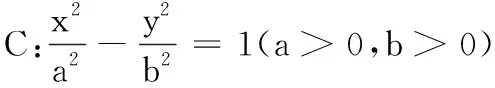
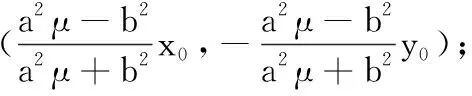
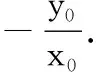
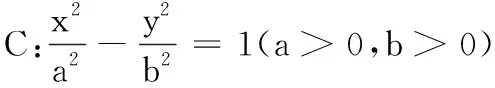
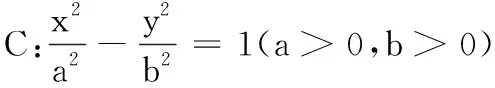
以上结论的证明类比于文[2]中椭圆情形的证法，故略.

结论5 已知抛物线C:y2=2px(p>0)上的定点P(x0,y0)，动点A，B(不同于P)，直线PA与PB的斜率之和为λ(λ为定值)，则

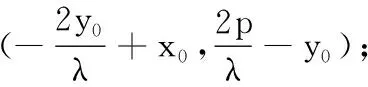
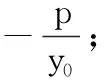
(3)当λ=0且y0=0时，直线AB的斜率不存在.

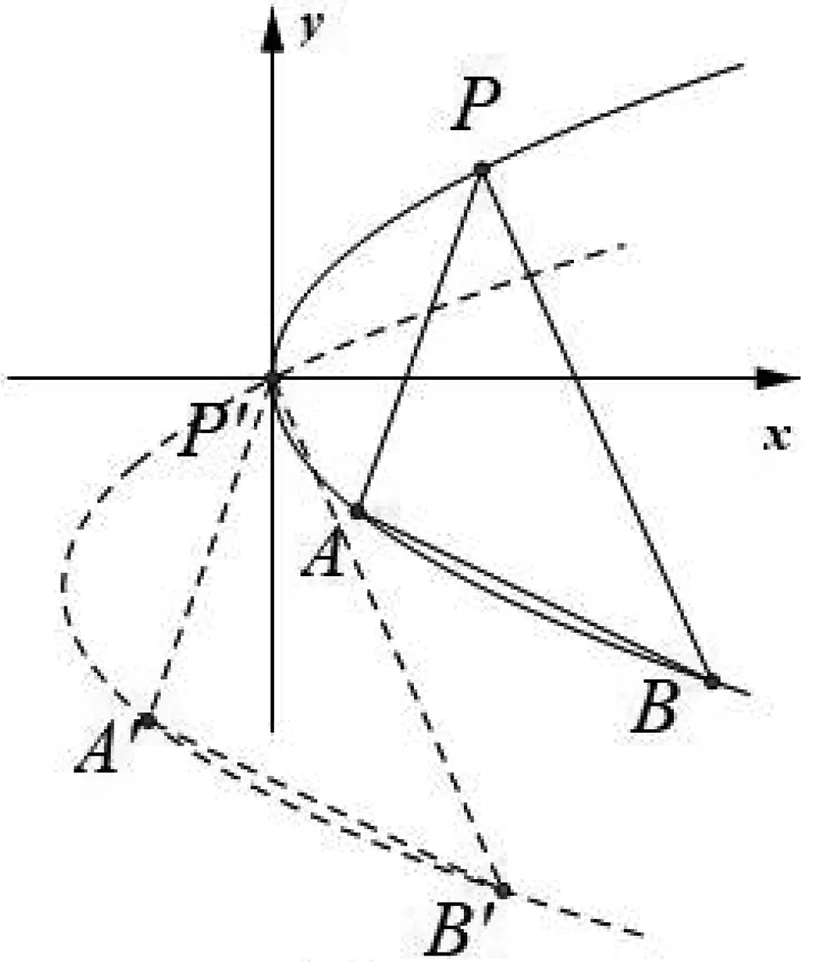
图1

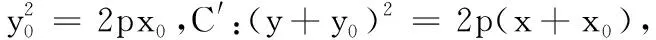
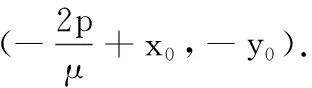
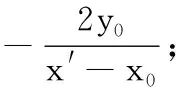
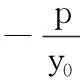
结论6-8的证明与结论5方法类似，故略.解题教学不应仅仅止步于问题的解决，而应尝试从不同角度分析问题，寻求不同的解法，把握各知识点之间的联系，探寻题目背后的秘密，锻炼思维的广度与深度.